引言

从本节开始将介绍集成学习的思想，本节将介绍统计机器学习中用来衡量模型的重要指标——偏差与方差。

偏差、方差简单介绍

在统计学习中通常会使用方差($\text{Variance}$)和偏差($\text{Bias}$)来衡量一个模型的性能。
这里的性能是指模型预测结果的‘准确程度’。单从‘准确’这个词，我们可以将其与‘高斯分布’($\text{Gaussian Distribution}$)进行描述，而偏差与方差就是高斯分布的两个统计量。
假设某个真实模型的分布情况表示如下：

• 在极大似然估计与最大后验概率估计中介绍过，真实模型是一种客观存在的分布结果。
• 真实模型可以源源不断地生成出样本，但相反，我们可能极难得到‘真实模型’的相关信息。只能通过已知的真实样本对模型进行反推，而学习结果被称作‘预测模型’。
• 而预测模型也是一种分布，从该分布中产生的样本，我们可以称为‘幻想例子’$(\text{Fantasy Particle})$,相比于‘真实模型’产生的‘真实样本’，幻想粒子没有实际意义。但幻想粒子可以衡量‘预测模型’与‘真实模型’之间的关系。
• 如果‘幻想粒子’分布结果与‘真实样本’之间足够相似，那么可以认为‘预测模型’与‘真实模型’之间足够接近。
  

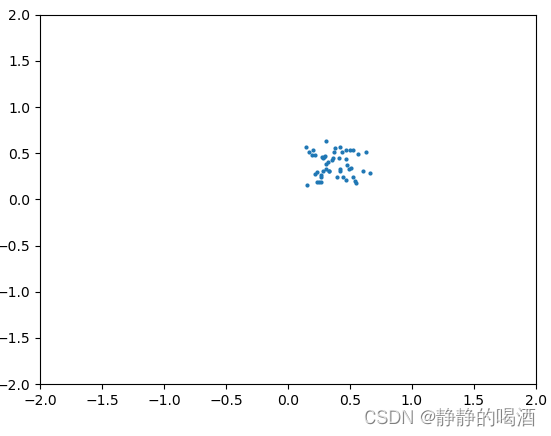
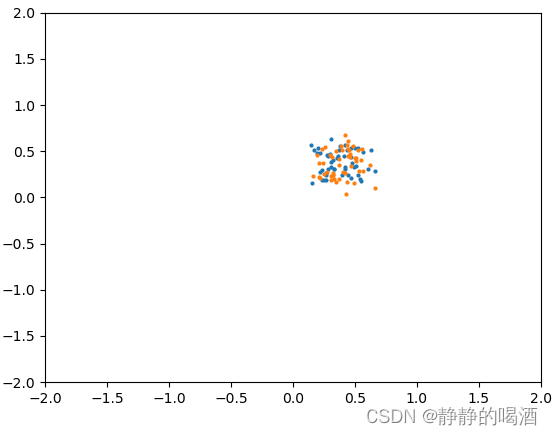
上述蓝色点表示真实模型中产生的真实样本；我们使用橙色点来表示预测模型的幻想粒子。关于幻想粒子分布可能出现的几种情况表示如下：

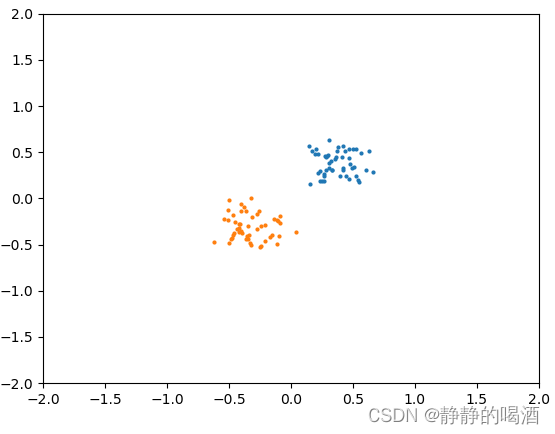
通过观察可发现，两个样本的所描述分布的紧凑程度大致相当；但幻想粒子的位置和真实样本的位置存在差别：
这里仅描述一个，后略。

• 从紧凑程度来看，两分布的规模/形状相似，属于低方差($\text{Low-Variance}$)；
• 从位置来看，两分布之间的位置差距较大，属于高偏差($\text{High-Bias}$)。

同理，高方差$(\text{High-Variance})$、低偏差$(\text{Low-Bias})$，意味着位置接近，但紧凑程度不匹配：

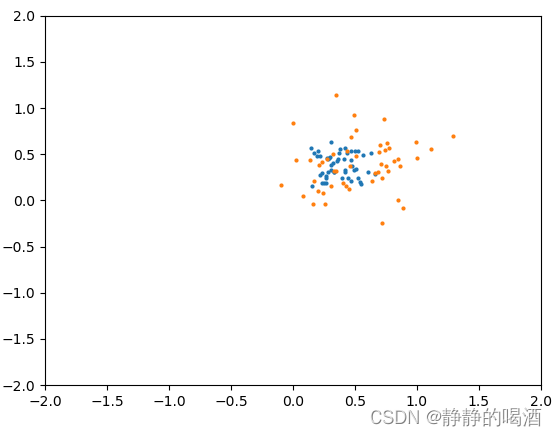
再如高偏差、高方差，相比于之前两种差距更大：

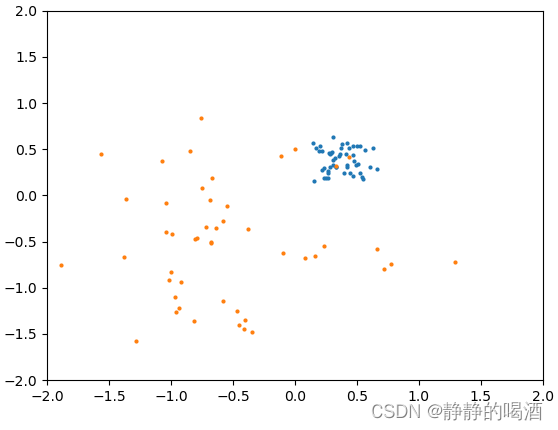
当然，作为预测任务，我们更期望预测模型更接近真实模型。即：低方差、低偏差：

方差、偏差的数学定义

这里假定一个真实模型/真实分布，并从该模型/分布中进行采样，得到真实数据集$\mathcal{D}$：
一般情况下，我们仅知道‘真实数据集’$\mathcal{D}$,而‘真实模型’是未知的。
$$\{\begin{array}{l}\text{Model : }\mathcal{Y}=f(\mathcal{X})+ϵ\\ \mathcal{D}={\left\{(x^{(i)},y^{(i)})\right\}}_{i=1}^N\text{from Model.}\end{array}$$
其中，样本标签$\mathcal{Y}$是由关于样本特征$\mathcal{X}$的函数$f(\mathcal{X})$加上一个 噪声($\text{Noise}$)$ϵ$ 组合而成。而我们的目标是从真实数据集$\mathcal{D}$学习出一个模型$\hat{f}$，使$\hat{f}$尽量与真实模型$f$近似。

这明显是一个简单的回归($\text{Regression}$)问题，我们完全可以使用均方误差($\text{Mean-Square Error,MSE}$)对该问题进行解决：
其中${\mathcal{Y}}^{(i)}$表示某个真实标签;${\mathcal{Y}}_{pred}^{(i)}$表示针对${\mathcal{Y}}^{(i)}$预测的标签结果。它们均是标量($\text{Scalar}$).
$$\text{MSE}=\frac{1}{N}\sum _{i=1}^N{\left({\mathcal{Y}}^{(i)}-{\mathcal{Y}}_{pred}^{(i)}\right)}^2$$

在$\text{MSE}$结果计算完，并使用梯度下降方法进行优化后，要如何衡量它：我们更希望该模型能够泛化到训练集内部没有的陌生样本。针对任意从真实模型中采样的样本特征$(\hat{x},\hat{y})\in f$，我们的预测结果${\hat{y}}_{pred}$总是和$\hat{y}$相近的。此时我们就认为学习模型$\hat{f}$与真实模型$f$是接近的。

关于均方误差的另一种解释可表示为：

• 将均值部分$\frac{1}{N}{\sum }_{i=1}^N$描述成期望形式，即预测标签${\mathcal{Y}}_{pred}^{(i)}$与真实标签${\mathcal{Y}}^{(i)}$之间差的平方的期望结果。
• 详细的计算技巧见机器学习(周志华著)P45.
• 其中下面三个期望内的项:$(f(x^{(i)})-\mathbb{E}[\hat{f}(x^{(i)})]{)}^2,{\left(\mathbb{E}[\hat{f}(x^{(i)})]-y(i)\right)}^2,{\left(\hat{f}(x^{(i)})-\mathbb{E}[\hat{f}(x^{(i)})]\right)}^2$,它们都是标量。因而期望是其自身。
  $$\begin{array}{rl}\text{MSE}& ={\mathbb{E}}_{\mathcal{D}}\left\{{\left[y^{(i)}-\hat{f}(x^{(i)})\right]}^2\right\}\\ & ={\mathbb{E}}_{\mathcal{D}}\left\{(f(x^{(i)})-\mathbb{E}[\hat{f}(x^{(i)})]{)}^2\right\}+{\mathbb{E}}_{\mathcal{D}}\left\{{\left(\mathbb{E}[\hat{f}(x^{(i)})]-y(i)\right)}^2\right\}+{\mathbb{E}}_{\mathcal{D}}\left\{{\left(\hat{f}(x^{(i)})-\mathbb{E}[\hat{f}(x^{(i)})]\right)}^2\right\}\\ & ={\text{Bias}}^2[\hat{f}(x^{(i)})]+\text{Var}[\hat{f}(x^{(i)})]+{ϵ}^2(x^{(i)},y^{(i)})\in \mathcal{D}\end{array}$$

至此，可以发现，算法的均方误差，也就是期望的泛化误差可以由偏差、方差、噪声之和的形式表示。

小插曲：最小二乘估计与均方误差

观察上述均方误差的式子，很容易想到最小二乘估计($\text{Least Square Estimation,LSE}$)：
$$\mathcal{L}(\mathcal{W},b)=\sum _{i=1}^N{\left|\left|{\mathcal{W}}^T{x}^{(i)}+b-y^{(i)}\right|\right|}_2^2(x^{(i)},y^{(i)})\in \mathcal{D}$$
它与均方误差都属于针对模型优化的策略/损失函数。从公式中观察，最明显的区别就是：最小二乘估计没有除以样本总数；而均方误差有。

从学习模式的角度观察，最小二乘估计是一种离线学习方法($\text{Off-line Learning}$)：即在真实数据集$\mathcal{D}=\{(x^{(i)},y^{(i)}){\}}_{i=1}^N$确定的条件下，基于模型$f(\mathcal{X})={\mathcal{W}}^T\mathcal{X}$，我们可以直接求得模型参数$\mathcal{W}$的解析解：

• 最小二乘估计的底层逻辑是极大似然估计$(\text{Maximum Likelihood Estimation,MLE})$，详细推导过程见机器学习笔记——线性回归
• 在这里，离线学习思想是指:给定完整的数据集，就可以对参数$\mathcal{W}$进行求解。关键点是‘完整’信息。
  $$\mathcal{W}=({\mathcal{X}}^T\mathcal{X}{)}^{-1}{\mathcal{X}}^T\mathcal{Y}$$

相反，均方误差是一种在线学习方法($\text{On-line Learning}$)，针对该损失函数，通常使用梯度下降($\text{Gradient Descent,GD}$)的方式寻找最优参数$\hat{\mathcal{W}}$的梯度方向，从而通过迭代实现近似求解：
迭代就意味着‘不止执行一次采样’。例如$\text{Mini-Batch}$梯度下降，可能需要从从数据集合$\mathcal{D}$中每次采集小批量样本对参数梯度进行计算。
$$\{\begin{array}{l}\mathcal{J}(\mathcal{W})=\frac{1}{N}{\sum }_{i=1}^N{\left[y^{(i)}-f_{\mathcal{W}}(x^{(i)})\right]}^2\\ \\ {\mathcal{W}}^{(t+1)}\Leftarrow {\mathcal{W}}^{(t)}-\eta {\nabla }_{\mathcal{W}}\mathcal{J}(\mathcal{W})\end{array}$$

从图像角度认识偏差、方差

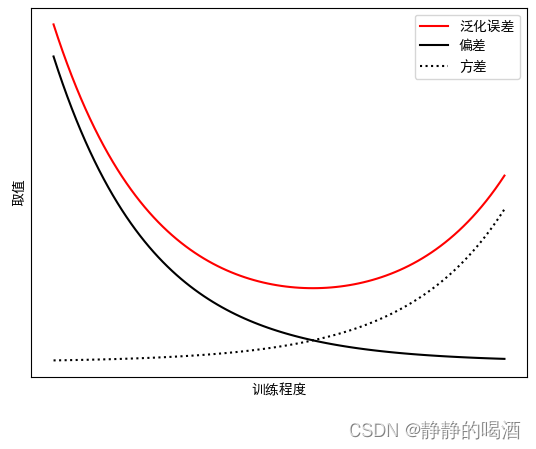
关于模型泛化误差、偏差、方差之间的关系表示为如下形式：

• 其中黑色的线表示偏差的平方${\text{Bias}}^2[\hat{f}(x^{(i)})]$。由于模型的初始参数一般情况下是随机初始化的，那么当模型训练初期，模型对于样本特征$x^{(i)}$的判别结果极大概率是不准确的，因而对应的纵坐标数值较大；

  随着训练过程中，模型参数的调整、更新，使得学习模型$\hat{f}(\mathcal{X})$可能可以学到真实模型$f(\mathcal{X})$想要表达的信息，因而使偏差的平方逐渐减小；

• 黑色虚线表示方差$\text{Var}[\hat{f}(x^{(i)})]$。它实际上与偏差之间存在冲突，这也被称为偏差-方差窘境($\text{Bias-Varance Dilemma}$)。它们之间的冲突具体表现为：

  模型训练初期，模型参数的表达不够准确，这会使学习模型$\hat{f}(\mathcal{X})$的拟合能力不够强，导致数据的样本特征的扰动不足以 使学习模型结果产生实时的、正确的变化。这意味着偏差较大，与真实模型的分布存在距离。

  当训练程度的加深，使得学习模型$\hat{f}(\mathcal{X})$的拟合能力逐渐变强，直到训练程度充足后，与初期相反，即便是样本特征的轻微扰动 都会引起学习模型的变化。此时学习模型则过多地关注噪声部分。最终导致方差越来越大。

• 而红色线则表示泛化误差——噪声、偏差、方差的融合。其中，噪声是真实数据自带的，可被视作一个固定常数；随着训练程度的增加，泛化误差结果存在相应变化：

  模型训练初期，参数训练不足的情况下：此时的泛化误差是由偏差主导的；

  模型训练后期，参数训练充足，并更加关注样本的噪声信息时，此时的泛化误差是由方差主导的。如果方差过大，意味着模型将训练集自身的、非全集的特性被学习到了，在此时过程中反而起到反效果，最终会产生过拟合($\text{Overfitting}$)。

减少偏差、方差的优化方法

为了得到更符合真实模型$f(\mathcal{X})$的学习模型$\hat{f}(\mathcal{X})$，我们需要降低噪声、偏差、方差结果对泛化误差的影响。

• 降低噪声：噪声是数据自身的属性，也就是说，噪声是客观的、不可以降低的误差。因而我们需要得到更精确、更干净的数据，以此来降低噪声。

• 降低偏差：一是因为训练程度不够高，使得模型参数未学习完全就被提前停止了，也就是欠拟合($\text{Underfitting}$)。那么则需要继续执行训练过程。

  二是因为模型的复杂度不够。当执行了很长的训练过程，但拟合能力依然较差时，我们需要提升模型的复杂度。例如增加隐藏层单元数量/隐藏层数量；以及相应的集成学习方法。如$\text{Boosting,Stacking}$；

• 降低方差：此时模型对于训练集的特征学习的过于复杂，与之相对的，尝试降低模型的复杂度；或者是对模型参数使用正则化，限制模型参数的学习范围；以及相应的集成学习方法。如$\text{Bagging Stacking}$；
  这里也包含其他预防过拟合的方式。

而$\text{Bagging,Boosting,Stacking}$都是集成学习的方法。集成学习($\text{Ensemble Learning}$)的核心思想是：通过多个模型来提升预测的性能。即多个模型通过一定方式结合起来，来降低方差、偏差。

相关参考：
5.1 方差与偏差【斯坦福21秋季：实用机器学习】
机器学习(周志华著)