LeetCode 62.不同路径 : https://leetcode.cn/problems/unique-paths

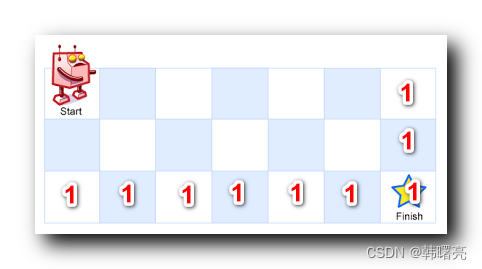
一个机器人位于一个 m x n 网格 的 左上角 （起始点在下图中标记为 “Start” ）。
机器人每次只能 向下或者向右 移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

一、问题分析

---

动态规划 可以解决 三类问题 :

• 求最值 : 最大值 , 最小值 等 ;
  • 大规模问题的结果 由 小规模问题 的计算结果 相加
  • 大规模问题的结果 由 小规模问题 的计算结果 取最大值
  • 大规模问题的结果 由 小规模问题 的计算结果 取最小值
• 可行性 : 是否可行 ;
  • 大规模问题的结果 由 小规模问题 的计算结果 必须全部可行
  • 大规模问题的结果 由 小规模问题 的计算结果 只要有一个可行即可
  • 大规模问题的结果 由 小规模问题 的计算结果 没有可行结果
• 方案数 :
  • 大规模问题的结果 由 小规模问题 的计算结果 可行方案总数

在本示例中 , 使用动态规划 求的是 可行方案总数 ;

在 m x n 网格中 , 只能向右走 或 向下走 ;

将 大规模问题 拆解成 小规模问题 时 , 其依赖关系 是有 方向性的 ;

二、自顶向下的动态规划

---

1、动态规划状态 State

使用 二维数组 dp 保存 动态规划的 状态 State ,

dp[i][j] 表示 从 (0, 0) 位置出发 , 到 (i, j) 位置的方案总数 ;

2、动态规划初始化 Initialize

在 初始位置 (0 , 0) 位置 的方案数 , 肯定为 1 , 因此有 dp[0][0] = 1 ;

最左侧的一列 , 只能向下走 , 其方案数也为 1 , 因此有 dp[i][0] = 1 ;

最上方的一排 , 只能向右走 , 其方案数也为 1 , 因此有 dp[0][j] = 1 ;

3、动态规划方程 Function

由于 运动时 , 只能 向右 或 向下 走 , 走到 (i , j) 只能是从 左边 (i - 1, j) 或 上边 (i , j-1) 位置走过来 ,

这里可以得到依赖关系 : dp[i][j] = dp[i-1][j] + dp[i][j-1]

4、动态规划答案 Answer

最终的 从 左上角 (0 , 0) 位置 走到 右下角 (m , n) 位置 的方案总数就是 状态 State 中的 dp[m - 1][n - 1] 数值 ;

5、代码示例

代码示例 :

public class Solution {

    /**
     * 不同路径
     * @param m 网格行数
     * @param n 网格列数
     * @return
     */
    public int uniquePaths(int m, int n) {

        // 1. 动态规划状态 State
        // dp[i][j] 表示 从 (0, 0) 位置出发 , 到 (i, j) 位置的方案总数 ;
        int[][] dp = new int[m][n];

        // 2. 动态规划初始化 Initialize
        // 最左侧的一列 , 只能向下走 , 其方案数也为 1 , 因此有 dp[i][0] = 1 ;
        for (int i = 0; i < m; ++i) {
            dp[i][0] = 1;
        }
        // 最上方的一排 , 只能向右走 , 其方案数也为 1 , 因此有 dp[0][j] = 1 ;
        for (int j = 0; j < n; ++j) {
            dp[0][j] = 1;
        }

        // 3. 动态规划方程 Function
        // 运动时 , 只能 向右 或 向下 走 ,
        // 走到 (i , j) 只能是从 左边 (i - 1, j) 或 上边 (i , j-1) 位置走过来 ,
        // 这里可以得到依赖关系 : dp[i][j] = dp[i-1][j] + dp[i][j-1]
        for (int i = 1; i < m; ++i) {
            for (int j = 1; j < n; ++j) {
                dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
            }
        }

        // 4. 动态规划答案 Answer
        // 最终的 从 左上角 (0 , 0) 位置 走到 右下角 (m , n) 位置
        // 的方案总数就是 状态 State 中的 dp[m - 1][n - 1] 数值 ;
        return dp[m - 1][n - 1];
    }

    public static void main(String[] args) {
        int minTotal = new Solution().uniquePaths(3, 7);
        System.out.println("3 x 7 网格方案数为 : " + minTotal);
    }
}

执行结果 :

3 x 7 网格方案数为 : 28

三、自底向上的动态规划

---

1、动态规划状态 State

使用 二维数组 dp 保存 动态规划的 状态 State ,

dp[i][j] 表示 从 (i , j) 位置出发 , 到 (m - 1, n - 1) 位置的方案总数 ;

2、动态规划初始化 Initialize

在 终点位置 (m - 1, n - 1) 位置 到 (m - 1, n - 1) 位置的方案总数 , 肯定为 1 , 因此有 dp[m - 1][n - 1] = 1 ;

最右侧的一列 , 只能向下走 , 到 (m - 1, n - 1) 位置的方案总数 也为 1 , 因此有 dp[i][n - 1] = 1 ;

最下方的一排 , 只能向右走 , 其 到 (m - 1, n - 1) 位置的方案总数 方案数也为 1 , 因此有 dp[m - 1][j] = 1 ;

3、动态规划方程 Function

由于 运动时 , 只能 向右 或 向下 走 , 从 (i , j) 走到 ( m - 1 , n - 1 ) 只能是走 右边 (i + 1, j) 或 下边 (i , j + 1) 位置 ,

即 从 (i , j) 走到 ( m - 1 , n - 1 ) 位置的方案数 , 依赖于

• 从 (i + 1, j) 走到 ( m - 1 , n - 1 ) 位置的方案数
• 从 (i , j + 1) 走到 ( m - 1 , n - 1 ) 位置的方案数

之和 ;

这里可以得到依赖关系 : dp[i][j] = dp[i+1][j] + dp[i][j+1]

4、动态规划答案 Answer

最终的 从 左上角 (0 , 0) 位置 走到 右下角 (m , n) 位置 的方案总数就是 状态 State 中的 dp[0][0] 数值 ;

5、代码示例

代码示例 :

public class Solution {

    /**
     * 不同路径
     * @param m 网格行数
     * @param n 网格列数
     * @return
     */
    public int uniquePaths(int m, int n) {

        // 1. 动态规划状态 State
        // dp[i][j] 表示 从 (i , j) 位置出发 , 到 (m - 1, n - 1) 位置的方案总数 ;
        int[][] dp = new int[m][n];

        // 2. 动态规划初始化 Initialize
        // 最右侧的一列 , 只能向下走 , 到 (m - 1, n - 1) 位置的方案总数 也为 1 ,
        // 因此有 dp[i][n - 1] = 1 ;
        for (int i = 0; i < m; ++i) {
            dp[i][n - 1] = 1;
        }
        // 最下方的一排 , 只能向右走 , 其 到 (m - 1, n - 1) 位置的方案总数 方案数也为 1 ,
        // 因此有 dp[m - 1][j] = 1 ;
        for (int j = 0; j < n; ++j) {
            dp[m - 1][j] = 1;
        }

        // 3. 动态规划方程 Function
        // 由于 运动时 , 只能 向右 或 向下 走 ,
        // 从 (i , j) 走到 ( m - 1 , n - 1 ) 只能是走 右边 (i + 1, j) 或 下边 (i , j + 1) 位置 ,
        // 即 从 (i , j) 走到 ( m - 1 , n - 1 ) 位置的方案数 , 依赖于
        // 从 (i + 1, j) 走到 ( m - 1 , n - 1 ) 位置的方案数
        // 从 (i , j + 1) 走到 ( m - 1 , n - 1 ) 位置的方案数
        // 之和
        for (int i = m - 2; i >= 0; i--) {
            for (int j = n - 2; j >= 0; j--) {
                dp[i][j] = dp[i + 1][j] + dp[i][j + 1];
            }
        }

        // 4. 动态规划答案 Answer
        // 最终的 从 左上角 (0 , 0) 位置 走到 右下角 (m , n) 位置
        // 的方案总数就是 状态 State 中的 dp[0][0] 数值 ;
        return dp[0][0];
    }

    public static void main(String[] args) {
        int minTotal = new Solution().uniquePaths(3, 7);
        System.out.println("3 x 7 网格方案数为 : " + minTotal);
    }
}

执行结果 :

3 x 7 网格方案数为 : 28