提供了编程的基础技术教程

zl程序教程

您现在的位置是：首页 >  硬件

当前栏目

机器学习中的时间序列预测模型

机器序列学习 时间 模型 预测
2023-09-11 14:19:29 时间

1.概述

        在机器学习的各类方法中，有一类主要能用于时间序列预测的模型，包括但不限于自回归模型AR、滑动平均MA、融合AR与MA的ARIMA、隐马尔可夫模型HMM、卡尔曼滤波KF、循环神经网络RNN/LSTM等，本文对其做基本的阐述并说明其各自特点与应用场景。

2.时间序列模型

        时间序列是按照一定的时间间隔排列的一组数据，其时间间隔可以是任意的时间单位，如小时、日、周、月等。比如，产品月均销售趋势、股市K线图走势、实时翻译的语音信号、机器人移动轨迹等这些数据形成了一定时间间隔且前后具有一定的延续性与关联性。 通过对这些时间序列的分析，从中发现和揭示现象发展变化的规律，然后将这些知识和信息用于预测。

        比如销售量是上升还是下降，销售量是否与季节有关，是否可以根据现有的数据预测未来一年的销售额等。 对于时间序列的预测，由于很难确定它与其它变量之间的关系，这时我们就不能用回归去预测，而应使用时间序列方法进行预测。采用时间序列分析进行预测时需要一系列的模型，这种模型称为时间序列模型。以下对其分别进行阐述。时间序列对应的机器学习通常属于在线学习 online learning。

2.1 AR与MA相关模型

2.1.1 自回归模型(Auto-Regressive model)

        自回归模型AR，是利用当前时刻之前若干时刻的随机变量的线性组合来描述以后某时刻随机变量的线性回归模型，自回归模型反映了序列数据当前值与前期 p个数值之间（对应 p 阶自回归模型）的相关关系，也就是说当前值可表示为前 p 项数值的线性组合与白噪声序列的函数。其中白噪声可以看作随机序列，序列的均值为0。自回归模型反映了具有统计上显著的滞后自相关性。p阶自回归模型的具体表达式如下

                                \large x_t=\phi_0 +\phi _{1}x_{t-1}+\phi _{2}x_{t-2}+...+\phi _{p}x_{t-p}+u_t

对于1 阶自相关性，上述模型简化为AR(1)，具体如下

                                        \large x_t=\phi_0 +\phi _{1}x_{t-1}+u_t

其中 u_t 是独立同分布的白噪音序列，其均值为0、方差为 \sigma_u^2  。\phi_0 +\phi _{1}x_{t-1} 这部分取决于过去的观测，u_t 是过去无法预测的部分。该模型的形式与简单线性回归模型相同，当x_t 被其对数波动率取代时，这个简单模型可广泛应用于随机波动率建模。

2.1.2 滑动平均(Moving Average)

        所谓滑动平均MA就是以一定的窗口为单位，在指定的窗口内将数据取平均，可以是简单平均也可以是加权平均。

        对于简单滑动平均

                      \large \hat{x}_{t+1}=\hat{\mu}_{t}=\frac{1}{t}\sum_{n=1}^{t}x_n=\frac{1}{t}((t-1)\hat{\mu}_{t-1}+x_{t}) =\hat{\mu}_{t-1}+\frac{1}{t}(x_{t}-\hat{\mu}_{t-1})

        从中可以看出，一个新的估计值等于旧的估计值加上一个修正项，通常修正项的添加可适用于在线学习（online learning）的不断修正。

        对于加权的滑动平均（q 阶滑动平均的通用表达式）

                           \large x_t=\mu+u_t+\theta _{1}u_{t-1}+\theta_{2}u_{t-2}+...+\theta_{q}u_{t-q}=\mu+u_t+\sum_{i=1}^{q}\theta_i u_{t-i}

        MA(q)模型总是平稳的，因为它是有限的白噪声过程的线性组合,只考虑滞后的前 q项，相应的系数\theta_i(1\leq i \leq q ) 都是常数,其它项的影响系数都为0。其中 x_t 是待预测值，白噪声 u_t \sim N(0,\sigma_u^2)，视为独立同分布的正态时间序列。

        MA模型具有可逆性(Invertibility)，可逆性提供了一个简单的方法来获得冲击值（噪声序列）。零均值MA(1)模型可改写为

                                \large u_t=x_t-\theta_1u_{t-1}=x_t-\theta_1x_{t-1}-\theta_1^2x_{t-2}-...

        直观上可知，  随系数阶次的增加其影响应更小（时序距离更远），当阶次趋于无穷时相应的影响应趋于0。因此为保证MA(1)具有可逆性，通常要求  \left | \theta \right |<1。

2.1.3 指数滑动平均(Expotential Moving Average)

        指数滑动平均的表达式如下

                                                \large \hat{x}_{t+1}=\hat{\mu}_t=\beta\hat{\mu}_{t-1}+(1-\beta)x_t

        待预测值 \hat{x}_{t+1} ，对应 t+1 时刻，其中，0<\beta<1。一个数据点在时间 k 步之后的影响权重为 \beta^k(1-\beta)。因此随时间的推移，距离当前时刻越远的时间点的贡献呈指数下降。

                                    \large \begin{align} \hat{\mu}_t &=\beta\hat{\mu}_{t-1}+(1-\beta)x_t \nonumber \\ &=\beta\hat{\mu}_{t-2}+\beta(1-\beta)x_{t-1}+(1-\beta)x_t \nonumber \\ &=\beta^t x_0+(1-\beta)\beta^{t-1}x_{1}+...+(1-\beta)\beta x_{t-1} +(1-\beta)x_t \nonumber \end{align}

        根据指数级数的求和

                                \large \beta^t+\beta^{t-1}+...+\beta^1+\beta^0=\frac{1-\beta^{t+1}}{1-\beta}

        因此得到

                                \large (1-\beta)\sum_{k=0}^{t}\beta^k=(1-\beta)\frac{1-\beta^{t+1}}{1-\beta}=1-\beta^{t+1}

        因为 0<\beta<1，当 t\rightarrow \infty 时， \beta^{t+1}\rightarrow 0 , 也就是说 \beta 取值越小，对过去遗忘的越快，也就是更倾向于当前的数据。因为 \hat{\mu}_0=0 作为初始的估计，通过比例系数修正原估计值，得到

                                                         \large \tilde{\mu}_t=\frac{\hat{\mu}_t}{1-\beta^t}

2.1.4 ARMA(Autoregressive Moving Average)

        为了克服单独的AR和MA的不足，从而解决高阶的问题，引入自回归滑动平均(ARMA)模型，也就是AR与MA的结合，具体的表达式如下：

 \large x_t=\phi_0 +\phi _{1}x_{t-1}+\phi _{2}x_{t-2}+...+\phi _{p}x_{t-p}+u_t+\theta _{1}u_{t-1}+\theta_{2}u_{t-2}+...+\theta_{q}u_{t-q}

        用滞后算子来表示ARMA(p,q),得到如下表达式

                                \large \left ( 1-\sum_{i=1}^{p} \phi _i L^i \right ) x_t= \phi _0+ \sum_{i=0}^{q} \theta _i u_{t-i}

        其中 \theta_0=1。L 称为滞后算子，是指将一个以一定时间间隔定期采样的变量的时间指标向后移动一个单位时间。将滞后算子应用到一个泛型变量x_t  上，得到该变量在时刻 t-1 时的值，即Lx_t=x_{t-1}  。滞后算子可以提升为幂次，例如L^2x_t=x_{t-2}  。也可以形成滞后算子的多项式

                                \large a(L)=a_0+a_1L+...a_pL^p

                                \large a(L)x_t=a_0x_t+a_1x_{t-1}+...a_px_{t-p}

        若\left | \rho \right | <1,则根据等比数列求和公式可得到：

                         \large (1-\rho L)^{-1}=\sum_{i=0}^{\infty}\rho^iL^i

        其中定义有如下关系式：

                                \large (1-\rho L)(1-\rho L)^{-1}\equiv 1

2.1.5 ARIMA(Autoregressive Moving Average)

        差分自回归滑动平均模型（ARIMA），综合了三项 AR、I（integration）、MA，是在ARMA基础上改进而来的模型。

        ARMA模型的平稳性要求 x 的均值、方差和自协方差都是与时间无关的、有限的常数，也就说ARMA模型是针对平稳时间序列建立的模型，只能处理平稳序列。

        而ARIMA模型是针对非平稳时间序列建模。换句话说，非平稳时间序列要建立ARMA模型，首先需要经过差分转化为平稳时间序列，然后建立ARMA模型。

        如果非平稳时间序列 x_t 经过 d 次差分后的平稳序列z_t服从ARMA(p, q)模型，那么称原始序列x_t 服从ARIMA(p, d, q)模型。也就是说，原始序列是I(d) 序列，d 次差分后是平稳序列I(0)。平稳序列I(0)服从ARMA模型，而非平稳序列I(d) 服从ARIMA模型。

        基于ARMA添加差分处理，在前述模型上多了一个差分阶数需要进行确定，表达式如下：

                        \large \left ( 1-\sum_{i=1}^{p} \phi _i L^i \right )\left ( 1-L \right )^dx_t=\left ( 1+\sum_{i=1}^{q} \theta_i L^i \right )\epsilon_t

        由以上分析可知，建立一个ARIMA模型需要解决以下3个问题：

        （1）将非平稳序列转化为平稳序列。

        （2）确定模型的形式。即模型属于AR、MA、ARMA中的哪一种，主要通过模型识别确定。

        （3）确定变量的滞后阶数，即求和项。这也是通过模型识别完成的。

2.2 Prophet

        Prophet是由Facebook 开发的一个流行的时间序列预测库，它拟合的是一个广义的加性模型，相应的表达式如下

                                \large y(t)=g(t)+s(t)+h(t)+\omega ^Tx(t)+\varepsilon _t

        其中各项的表示形式如下：

        a) g(t)表示趋势项，模拟时间序列在非周期上面的变化趋势

        b) s(t)是季节项或称周期项(使用正弦基函数拟合的线性回归模型）,一般以周或者年为单位

        c) h(t)是稀疏的“假日效应”可选项，表示在当天是否存在节假日，模拟节假日的特殊影响

        d) x(t) 为可能滞后的协变量，w 是回归系数，实际应用中多数情况下可不考虑这一可选项

        e) \epsilon_t 是残留的噪声项，假定为iid高斯分布

        Prophet 算法通过分别拟合这几项，最后把它们累加起来就得到了时间序列的预测值。

        Prophet是回归模型，而不是自回归模型，因为它是给定时刻 \large t, 预测时间序列\large y_{1:T},并不考虑过去的观测值 \large y 。

         为了对时间依赖性建模，趋势项有两个重要的函数，一个是基于逻辑回归函数（logistic function）的，另一个是基于分段线性函数（piecewise linear function）的。

对于逻辑回归函数

                                                \large g(t)=\frac{C}{1+exp(-k(t-m))}

        这里的 C 称为曲线的最大渐近值，k表示曲线的增长率，m 表示偏移项。当C=1,k=1,m=0时，简化为常见的 sigmoid 函数的形式。

        实际应用中，三个参数 C,k,m不可能都为常数，而很有可能是随着时间的迁移而变化的，因此，在 Prophet 里面，Prophet原文作者考虑将这三个参数全部换成了随着时间而变化的函数，也就是

 C=C(t),k=k(t),m=m(t).

        现实的时间序列中，曲线的走势肯定不会一直保持不变，在某些特定情况或有某种潜在的周期影响下，曲线会发生变化，这个时候，就有所谓的变点检测，也就是所谓 change point detection，变点（change point）就是走势或趋势发生明显变化的点，类似于通常说的“拐点”。

对每一段的趋势和走势根据 change point 的情况而改变，由此得到分段的逻辑回归增长模型：

                                        \large g(t)=\frac{C}{(k+a(t)^T\delta) t+(m+a(t)^T\gamma)}

其中， \large k 是增长率，\large m是偏移量，a_j(t)=\mathbb{I}(t\geq s_j)，其中s_j 是第 j 个变化点对应的时刻，\delta _t \sim Laplace(\tau) 是变化的大小， \gamma_j = -s_j是为了使函数保持连续的添加项。\delta (t) 拉普拉斯先验。

对于分段线性函数

        此时若假定趋势函数g(t)是分段线性的，时间轴上有S个均匀分割的变化点（changepoints），相应的表示如下：

                                        \large g(t)=(k+a(t)^T\delta) t+(m+a(t)^T\gamma)

        为了确保了MAP参数估计是稀疏的，因此变化点（changepoints）边界之间的差异通常为0。

        季节性趋势是几乎所有的时间序列预测模型都会考虑的选项，这是因为时间序列通常会随着天，周，月，年等季节性的变化而呈现季节性的变化，也称为周期性的变化。对于周期函数而言，通常使用较多就是正弦、余弦函数。而在数学分析中，区间内的周期性函数可以通过正弦和余弦的函数的和来表示，那么s(t) 就可以采用如下的傅立叶级数表示：

                                \large s(t)=\sum_{n=1}^{N}((a_n \frac{\cos(2\pi nt)}{P})+(b_n \frac{\sin(2\pi nt)}{P}))

        在实际环境下，除了周末，同样有很多节假日，而且不同的国家有着不同的假期。在 Prophet 里面，通过考虑一个稀疏的假日效应可选项\small h(t)对节假日的影响程度（节假日效应）建模。

        由于每个节假日对时间序列的影响程度不一样，比如春节，国庆节是长假，元旦、劳动节是短假，不同的节假日可看成相互独立的模型，同时可以为不同的节假日设置不同的时间窗口值，表示该节假日会影响前后一段时间的时间序列。

        对于第 \small i个节假日而言，\small D_i 表示该节假日的前后一段时间。为了表示节假日效应，定义一个相应的指示函数（indicator function）\small \mathbb{I}({t\in D_i})，同时分配一个参数 \small \kappa _i  来表示节假日的影响范围。假定有 \small L个节假日，那么

                        ​​​​​​​        ​​​​​​​        \large h(t)=Z(t)\kappa=\sum_{i=1}^{L}\kappa_i \cdot \mathbb{I}({t\in D_i})

其中

                                         \large Z(t)=[{1({t\in D_1}}),{1({t\in D_2}}),...,{1({t\in D_L}})]

        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        \large \kappa=[\kappa_1,\kappa_2,...,\kappa_L]^T

        其中\small \kappa \sim Normal(0,\nu ^2) 并且该正态分布受到 \large \nu 这个指标影响。fbprophet模型中默认值取 10，当值越大时，表示节假日对模型的影响越大；当值越小时，表示节假日对模型的效果越小。可根据自己的情况自行调整。

        prophet 直观的可视化延时效果可详见 prophet 可视化。

2.3 Gaussian processes

        使用高斯过程也可以进行时间序列预测。其基本思想是将未知输出量建模为时间函数f(t)，并将f的先验表示为高斯过程；然后根据观察到的论据evidence，进一步更新之前的内容，并预测未来值。对于某些稳态核，可以将问题重新表述为线性高斯状态空间模型，如使用Kalman平滑滤波器在有限的时间内进行推测。该转换可利用Matren核精确完成，而高斯核（RBF）则可以近似地完成。实际应用中可考虑如下一个典型的高斯过程建模形成的一个复合高斯核模型：

                                        k(r)=k_1(r)+k_2(r)+k_3(r)+k_4(r)

其中 k_i(t,t')=k_i(t-t')对应第 i 个核函数。

为了捕捉长期平滑上升趋势，我们指定 k_1 为平方指数 (SE： squared exponential) 核函数，其中 \theta_0 表示幅度值，\theta_1是尺度因子，得到如下形式

                                                k_1(r)=\theta_0^2exp\left ( -\frac{r^2}{2 \theta_1^2} \right )

为了对周期性进行建模，我们借用了指数正弦平方核函数，周期参数设置为 1 年。 然而，由于不清楚季节性趋势是否刚好就是周期性的，我们将这个周期性核函数与另一个 SE核函数相乘，实现偏离周期性衰减的效果， 得到如下所示函数 k_2，其中 \theta_2是幅度值，\theta_3  是周期性分量的衰减时间，\theta_4 = 1是周期，\theta_5是周期分量的平滑度。

                                        k_2(r)=\theta_2^2exp\left ( -\frac{r^2}{2 \theta_3^2}-\theta_5sin^2\left (\frac{ \pi r}{\theta_4} \right ) \right )

为了模拟（小）中期不规则性，我们使用如下有理二次核函数

                                        k_3(r)=\theta_6^2\left [ 1+\frac{r^2}{2\theta_7^2\theta_8} \right ]^{-\theta_8}

其中\theta_6 是幅度，\theta_7 是典型的尺度因子，\theta_8 是形状参数。

最后一项对应独立噪声的大小，可以并入似然函数的观测噪声中。 对于相关噪声，我们使用另一个 SE 核函数

                                        k_4(r)=\theta_9^2exp\left ( -\frac{r^2}{2 \theta_{10}^2} \right )

我们可以通过优化关于\theta 的边际似然函数来拟合这个模型。

2.4 HMM

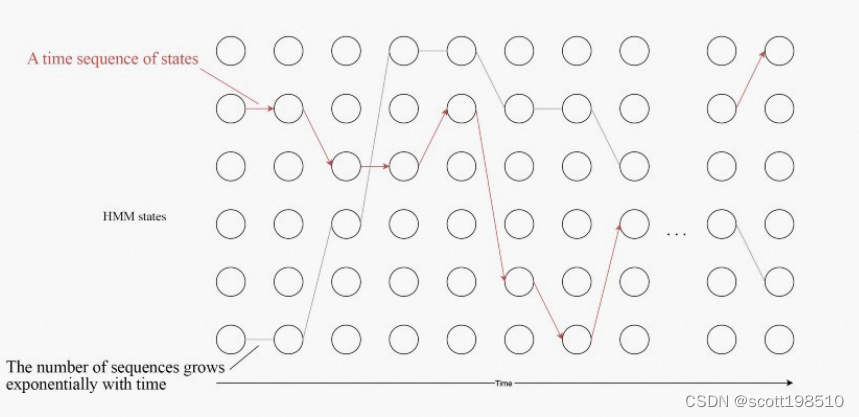
        隐马尔可夫模型（Hidden Markov model,HMM）是关于时序的概率模型，可用于序列标注问题的统计学建模，描述由一个隐马尔可夫链随机生成不可观测的状态随机序列，再由各个状态生成一个观测而产生观测随机序列的过程（因状态是隐式的所以而得名）。

        隐马尔可夫链随机生成的状态的序列称作状态序列。 每个状态生成一个观测，而由此产生的观测的随机序列称作观测序列。 序列的每一个位置又可以看作是一个时刻。

        在 HMM 中，我们通过使用t-1 和 t+1时刻的结果来解决时刻 t 的预测问题。下面的圆圈表示时刻 t 的 HMM 隐状态 j 。因此，即使状态序列的数量随时间呈指数级增长，假定其可以随时间递归地表示计算，那么我们也可以经线性化处理求解它。

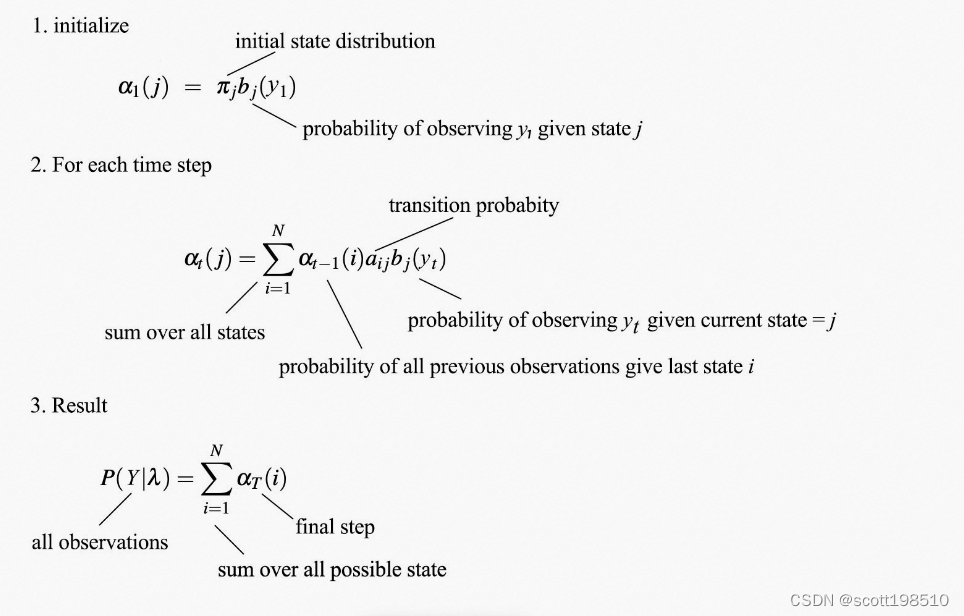
 定义在时间  t 的观测概率为：

        ​​​​​​​定义\alpha_t(j)为 t 时刻隐状态j 的前向概率，a_{ij}描述的是由前一时刻 t-1 的状态 i 转移到当前时刻 t 的状态 j 的概率。由于当前观测仅取决于当前状态，\alpha_t(j) 可表示为：

           

上述前向概率\alpha_t(j)它表示到时刻 t已知的部分观测序列为y_1,y_2,...,y_t,且t 时刻的状态为j 的概率，实际上是一个联合概率，记作如下：

        ​​​​​​​                        \alpha_t(j)=P(Y_1=y_1,Y_2=y_2,...,Y_t=y_t,x_t=j|\lambda)

 观测的似然概率P(Y|\lambda) 可通过以下各个时间步递归计算得到

再定义​​​​​后向概率\beta，它表示在相反方向上的概率（在时间 t 给定状态 j 的情况下看到所有即将到来的观测的概率），实际上是一个条件概率，具体如下

        ​​​​​​​        \beta_t(j)=P(Y_{t+1}=y_1,Y_{t+2}=y_2,...,Y_T=y_T|x_t=j,\lambda)​​​​​​​

可以用类似于\alpha 的递归方式计算，但方向相反（也称为反向算法）。

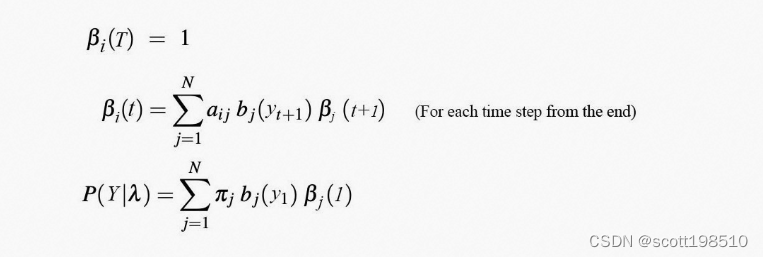
 要学习 HMM 模型，我们需要知道我们处于什么状态才能最好地解释观测结果。这将是状态概率\gamma,也就是给定所有观测值的前提下，在时间 t 状态是 i 的概率。

给定 HMM 模型参数模型参数\lambda=(A,B,\pi)固定，我们可以应用前向和后向算法从观测中计算得到\alpha 和 \beta 。可以通过简单地将\alpha 乘以 \beta来计算 \gamma ，然后对其进行重新归一化。

        ​​​​​​​        ​​​​​​​        ​​​​​​​

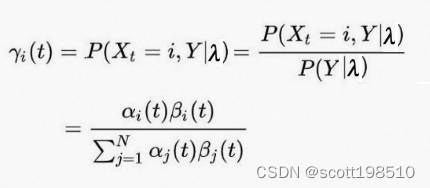
\xi是在给定所有观测值的情况下，在时间  t之后从状态 i 转移到 j的概率称为转移概率。它可以类似地由\alpha 和 \beta计算 得到

        ​​​​​​​        ​​​​​​​        ​​​​​​​

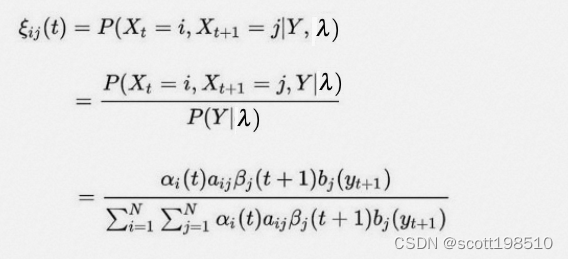
 采用EM算法求解得到是似然概率最大化的参数 a 和 b。

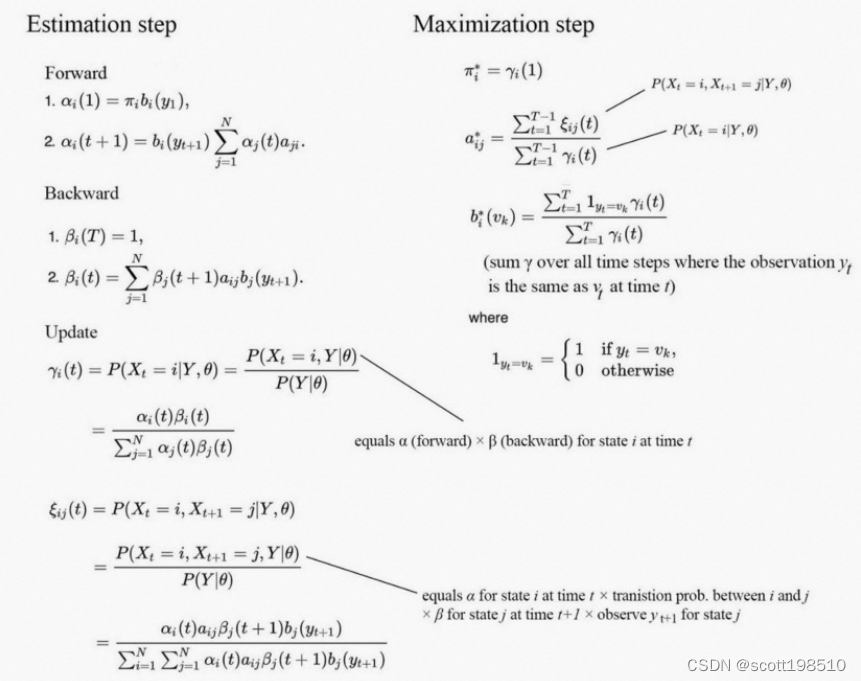
 HMM算法实现的完整迭代流程如下

2.5 KF

        卡尔曼滤波是一种通过给定观测值的情况下，对未知变量提供预测估计的算法。卡尔曼滤波器已经在导航与定位、位置追踪、金融时序数据预测等应用中表现出良好的实用性。卡尔曼滤波器具有表达形式简单，不需要太大的计算能力和存储空间的特点。

        卡尔曼滤波算法分为预测prediction和更新update两个阶段。“预测”和“更新”通常在不同的文献中也称为“传播”和修正。

Prediction:

                                \large \hat{x}_k^{-}=F\hat{x}_{k-1}^{+}+Bu_{k-1}                    （Predicted state estimate）

                                \large {P}_k^{-}=F{P}_{k-1}^{+}F^T+Q                        (Predicted error covariance)

Update:

                        ​​​​​​​        \large \tilde{​{y}}_k^{-}=z_k-H\hat{x}_k^{-}                                   (Measurement residual)

        ​​​​​​​        ​​​​​​​        ​​​​​​​        \large \large {K}_k^{}=P_k^{-}H^T(H{P}_{k}^{-}H^T+R)^{-1}     (Kalman gain)

                                \large \hat{x}_k^{+}=\hat{x}_k^{-}+K_k\tilde{y}                                  (Updated state estimate)

                                \large {P}_k^{+}=(I-K_kH){P}_k^{-}                        (Updated error covariance)

2.6 LSTM

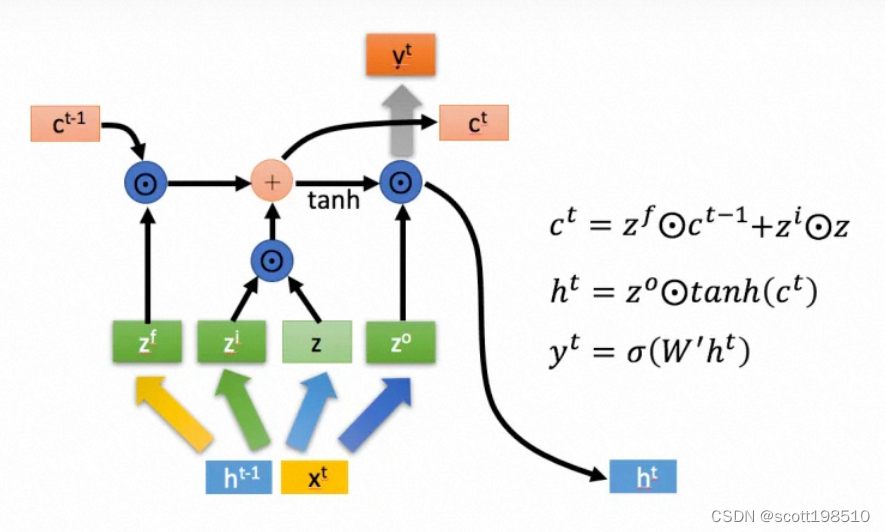
        长短时记忆模型(Long short-term memory, LSTM)是一种特殊的RNN，主要是为了解决长序列训练过程中的梯度消失和梯度爆炸问题。简单来说，就是相比普通的RNN，LSTM能够在更长的序列中有更好的表现。LSTM结构（图右）和普通RNN的主要输入输出区别如下所示。

        下面具体对LSTM的内部结构来进行剖析。

        首先使用LSTM的当前输入 x_t和上一个状态传递下来的 h_{t-1}​​​​​​​ 拼接训练得到四个状态。

         下面开始进一步介绍这四个状态在LSTM内部的使用。

2.7其它

3.应用举例

4.总结

       上述列出了常见不同时间序列学习模型的原理与数学形式。具体应用中，对于偏向自相关的时间序列，常见于经济、金融如股市、期货相关的价格走势等问题使用较多的是AR、MA、ARMA、 ARIMA，KF主要应用于物理模型，常见于航空航天等领域的组合导航、定位算法等，HMM主要应用于语音识别、自然语言处理的早期模型，RNN/LSTM作为深度学习大红大紫后大模型的主要组件，使用范围涵盖了图像、视觉、语音、自然语言处理等模式识别的几乎各个方面。  

相关文章