引言

本节针对精确推断之变量消去法中出现的存在环结构概率图的情况，介绍因子图(Factor Graph)，其主要将带环的无向图结构转化为因子图结构。

回顾：图结构相关思想

针对贝叶斯网络/马尔可夫随机场，可以通过因子分解的形式对结点变量集合$\mathcal{X}$的联合概率分布$\mathcal{P}(\mathcal{X})$进行表示：

• 贝叶斯网络(有向图)
  在这里同样需要注意，这里的$i$是结点变量的下标，它只能说‘有可能是特征下标’，即‘每个结点变量中均仅包含一个特征/变量’。
  $$\mathcal{P}(\mathcal{X})=\prod _{\mathcal{X}}\mathcal{P}(x_i\mid x_{pa(i)})$$
• 马尔可夫随机场(无向图)
  $$\mathcal{P}(\mathcal{X})\prod _{i=1}^{\mathcal{K}}{\psi }_{{\mathcal{C}}_i}(x_{{\mathcal{C}}_i})$$
  其中，$x_{{\mathcal{C}}_i}$表示编号为$i$的最大团，无向图中一共包含$\mathcal{K}$个极大团。而${\psi }_{{\mathcal{C}}_i}(x_{{\mathcal{C}}_i})$表示极大团$x_{{\mathcal{C}}_i}$对应的势函数结果。

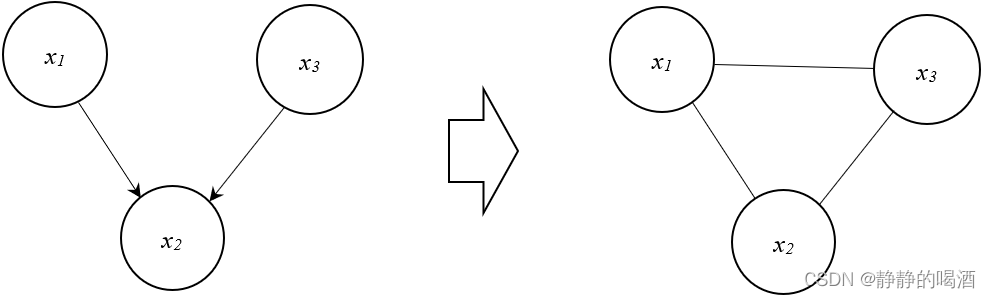
道德图的功能是将有向图转化为无向图，其主要针对贝叶斯网络中的$\mathcal{V}$型结构，将该结构中的双亲结点进行连接，从而 引入环结构：

因子图

因子图引入的朴素思想依然是在推断过程中简化运算，在变量消去法介绍中出现的贝叶斯网络结构，在推断过程中产生阻碍。实际上，如果不对变量消去法进行改进，一般的变量消去法只能处理无环的树形结构。

因此，引入因子图的结构方式，通过将有环结构的图修改成因子图的形式，从而使用精确推断对因子图进行处理。

因子图的特点

因子图的特点在于：将结点之间的因子关系直接表现在图上。
其对应公式表示如下：
$$\mathcal{P}(\mathcal{X})=\prod _{\mathcal{S}}{f}_{\mathcal{S}}({\mathcal{X}}_{\mathcal{S}})$$
其中$\mathcal{S}$表示图中结点变量集合的任意子集，相对应的${\mathcal{X}}_{\mathcal{S}}$表示$\mathcal{S}$子集对应在数据集合中的变量/特征集合。$f_{\mathcal{S}}$表示因子结点。
因子图示例如下：

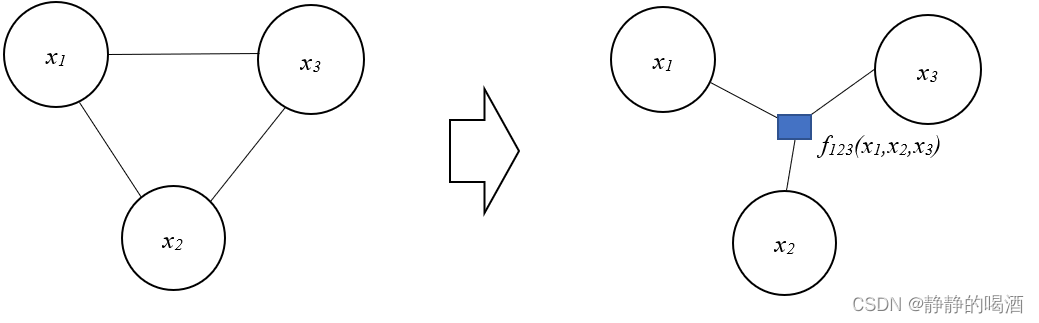
上述无向图中一共包含$3$个结点，并且包含环结构。右侧是它对应其中一种因子图表示。从而联合概率分布$\mathcal{P}(\mathcal{X})$可表示为：
$$\mathcal{P}(\mathcal{X})=f_{123}(x_1,x_2,x_3)$$
可以看出，变量结点之间不存在直接的边相关联，而是通过因子结点进行关联。
上述因子图并非唯一结果，由于$\mathcal{S}$集合的任意性，可以随意修改结点子集$\mathcal{S}$中的结点，从而构成一系列新的子集：
例如上图中的结点集合$\mathcal{X}$可以包含$3$个结点子集${\mathcal{S}}_1,{\mathcal{S}}_2,{\mathcal{S}}_3$，各结点子集中包含的结点信息表示如下：
S 1 = { x 1 , x 2 } S 2 = { x 2 , x 3 } S 3 = { x 1 , x 3 } \mathcal S_1 = \{x_1,x_2\} \\ \mathcal S_2 = \{x_2,x_3\} \\ \mathcal S_3 = \{x_1,x_3\} S1​={x1​,x2​}S2​={x2​,x3​}S3​={x1​,x3​}
那么对应的因子结点$f_1,f_2,f_3$在因子图中表示如下：

对应的联合概率分布$\mathcal{P}(\mathcal{X})$可表示为：
$$\mathcal{P}(\mathcal{X})=f_1(x_1,x_2)\cdot f_2(x_2,x_3)\cdot f_3(x_1,x_3)$$
更特殊的情况，结点子集也可存在仅包含一个结点的情况，这里不再赘述。
综上，因子图$\mathcal{G}(\mathcal{X},\mathcal{F},\mathcal{E})$中对于边$\mathcal{E}$的要求只需满足：
因子结点$f_j\in \mathcal{F}$和变量结点$x_k\in \mathcal{X}$之间存在边的充要条件是$x_k$在结点子集${\mathcal{S}}_j$内。即$x_k\in {\mathcal{S}}_j$。

基于因子分解的因子图本质上是对无向图因子分解的更泛化的表示。

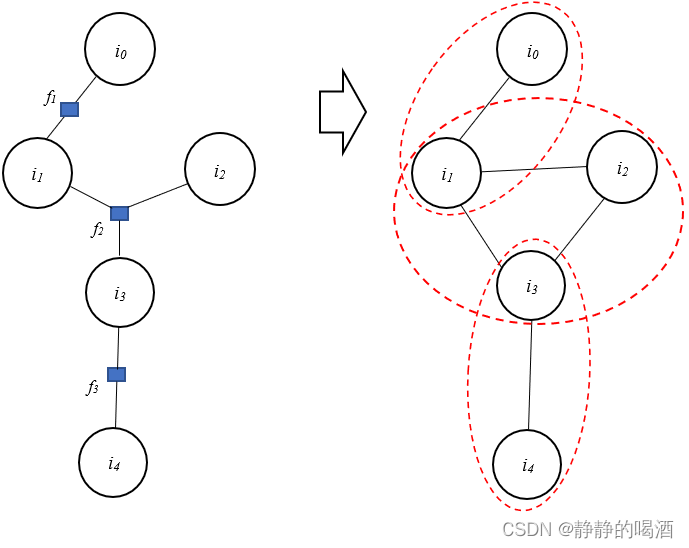
上述因子图与无向图的因子分解分别表示如下：
$$\{\begin{array}{l}\mathcal{P}(\mathcal{X})={\psi }_{01}(i_0,i_1)\cdot {\psi }_{123}(x_1,x_2,x_3)\cdot {\psi }_{34}(i_3,i_4)\\ \mathcal{P}(\mathcal{X})=f_1(i_0,i_1)\cdot f_2(i_1,i_2,i_3)\cdot f_3(i_3,i_4)\end{array}$$
从变量结点归属结点子集的角度，上述两个公式之间没有区别。我们可以将因子图看作是因子分解的进一步分解：
上述无向图同样存在‘特殊情况’。$i_1,i_2,i_3$组成的结点子集，既是‘环状结构’，也是‘极大团’。如果结点数量多起来，可能出现‘存在环结构但不是极大团的情况’。那时无向图可能需要重新寻找极大团；
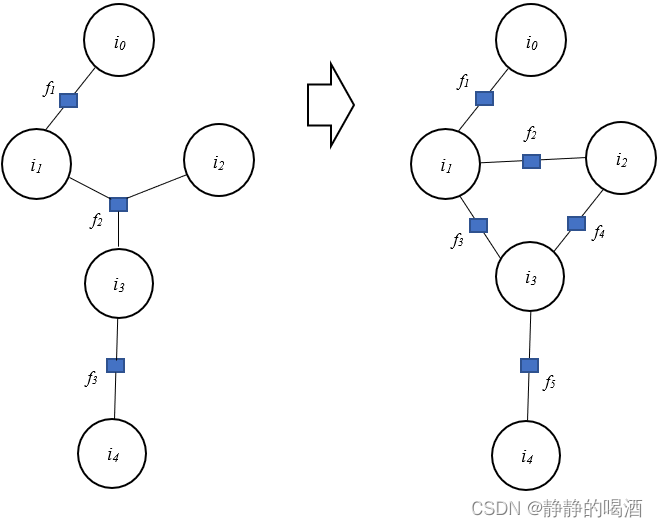
但‘因子图’并不存在这种限制，因为‘结点子集’$\mathcal{S}$可以是‘结点变量’的任意子集。相比于无向图操作，因子图的‘因子结点’可以将图划分的更加细致。

至此，概率图模型部分介绍结束，下一节将介绍线性动态系统(Kalman Filter)。

相关参考：
机器学习-概率图模型-概念补充-因子图（Factor Graph）
因子图-百度百科