算法设计 - 递归
目录
什么是递归?
函数递归
在成熟的编程语言中,函数都支持递归调用,即函数递归,它指的就是函数内部调用自身,举个例子(JavaScript):
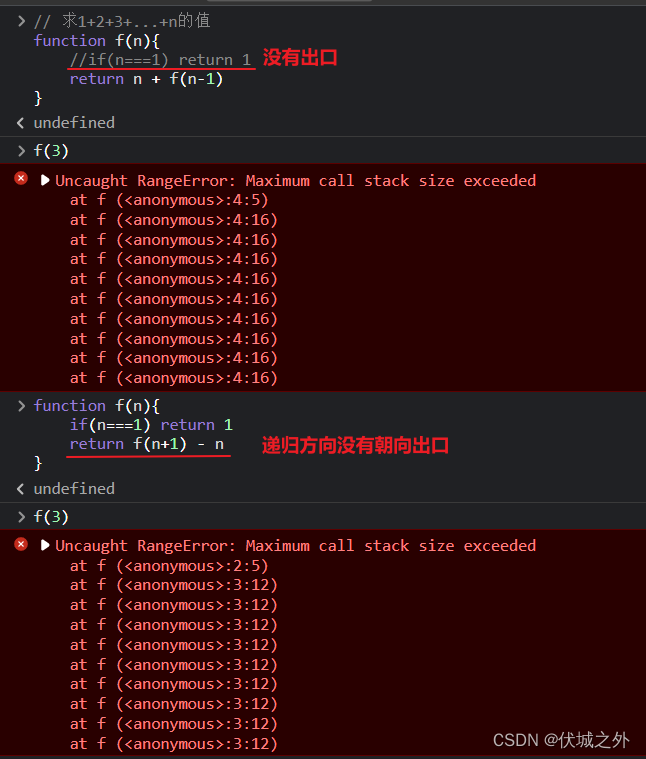
// 求1+2+3+...+n的值
function f(n){
if(n===1) return 1
return n + f(n-1)
}在JavaScript执行引擎中,每次函数调用都会创建一个函数执行上下文(栈帧),并推入执行栈(栈内存)中,当函数调用结束,则对应函数执行上下文从执行栈中出栈。
假设我们执行f(3),则上面程序运行时栈内存最大占用时如下:
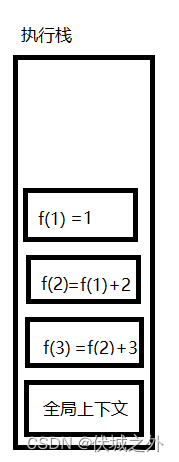
我们发现,若函数发生递归调用,则外层函数必须要等待内层函数递归调用结束,自身的调用才能结束。
所以正确的函数递归需要:
- 具备出口条件(递归结束条件)
- 具备朝向出口的递归方向
上面程序中,if(n===1) return 1就是f(n)的出口条件,f(n) = fn(n-1) + n 就是 f(n) 的递归方向,即不断n-1,最终让n=0。
如果函数递归不具备这两个条件,则会导致:栈内存溢出
递归算法
所谓算法,即规律。所以设计算法,即找规律。
而找规律的方式无外乎两种:
- 基于事物内部要素找规律,即找f(n)和n的关系
- 基于事物与事物之间的关系找规律,即找f(n) 和 f(n-?)的关系
其中第二种方式,最终也能间接产生f(n)和n之间的关系。
如果单从性能上来看,肯定是f(n)和n的之间的直接关系的性能好,但是从算法设计的难易度上来说,肯定是找f(n) 和 f(n-?)的关系更容易。
比如求1~n整数的和sum(n),例如
- sum(1) = 1
- sum(2) = 3
- sun(3) = 6
- sun(4) = 10
这里我直接给出n和sum(n)的直接关系:sum(n) = n(n+1)/2
大家觉得如果没有学过高斯求和公式,大家能够直接想出上面的规律吗?
但是,我们可以非常容易找出sum(n)和sum(n-1)之间的关系:
sum(n) = sum(n-1) + n;n>1
如果我们将上面公式写成函数表示,则
function sum(n) {
if(n>1) return sum(n-1) + n
}这不就是函数递归嘛!
但是这个递归有漏洞,那就是没有递归出口,即n不停-1迟早有n变为1的时候,所以我们应该为其添加n=1的出口条件
function sum(n) {
if(n===1) return 1
ireturn sum(n-1) + n
}因此,我们将找f(n)和f(n-?)之间规律的算法就叫做递归算法。
递归算法可以通过找f(n)和f(n-?)之间地关系,来间接地建立起f(n)和n的关系。
递归思想
递归思想由两部分组成:
- 分解:把一个问题划分为k个规模更小的子问题,然后用同样的方法求解规模更小的子问题。如果子问题不能实现简单求解,则基于一代子问题继续分解出规模更小的二代子问题,如此下去,直到n代子问题的规模小到可以被简单求解为止。
- 合并:将子问题的解按照递归回溯流程进行合并,最终就能得到原始问题的解。
我们之前了解了递归算法,其实就是找事物与事物之间的关系,比如f(n)和f(n-?)的关系。
而这种关系,其实是通过不断缩小问题规模来建立的。
什么意思呢?比如:
我们已经知道了 sum(n) = sum(n-1) + n,现在求sum(6),则:
sum(6) = sum(5) + 6
此时,我们想要求sum(6),则必须求得sum(5),也就是说,我们将求解sum(6)的问题,变成了求解sum(5)的问题,这意味着问题的规模缩小了。
而随着问题规模的不断缩小:
sum(5) = sum(4) + 5
sum(4) = sum(3) + 4
sum(3) = sum(2) + 3
sum(2) = sum(1) + 2
最终必然缩小到了一个base case上,即递归出口,即此时规模的问题可以被简单求解:
sum(1) = 1
而当base case返回解时,前面的大规模的问题,又会像多米诺骨牌到下一样可以被依次求解,这个过程即递归函数的回溯结果过程。
所以递归思想,即将大规模的问题不断缩小,知道变成base case的求解,然后根据递归回溯,将小规模问题的解不断回溯,最终合并为大规模问题的解。
递归算法的基本设计步骤
- 找到问题的最小规模的解(也可以理解为base case、递归出口等),如fibnaci数列的f(1) = 1,f(2) =1
- 将规模大的问题,一步步分解为规模小的子问题,并确保分解方向最终可以通往递归出口,如求1~100以内数的和,f(n) = n + f(n-1),最终会分解到 f(2) = 1 + f(1),而f(1)就是递归出口,它的解可以简单求出为1
- 合并子问题的解得到原始问题的解,需要注意的是,这里的子问题的解的合并一般就是走递归的回溯流程。
这三步中最难的就是第二步,即问题的分解过程,或者说递归公式、分解方程的总结,或者用英语说叫 relate hard case to simple case。即从特殊到一般,从具体到抽象。
目前我们用到的求1~100内整数和,和求fibnaci数的分解方程都是非常简单的,或是一眼看出,或是题目点明。
但是大部分问题的分解方程都是无法直观看出来的,此时我们就需要准备大量的、特殊的、具体的、规模小的、多层级的子问题及它们的解,并且从多层级的具体子问题的解中找到一般的、抽象的、普适的规律。
下面我们会通过几个递归算法实例,来着重练习,如何进行问题分解
递归算法实例
网格移动路径
一个机器人位于一个 m x n 网格的左上角。机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角。问总共有多少条不同的路径?
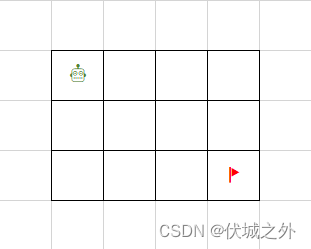
首先我读完这道题目,我脑子里大概已经模拟出来上面示例图中机器人的几种移动路径,但是让我根据脑海中已有的几条路径总结出规律,我是一点思路也没有的,此时我该怎么办?用递归思想啊!
递归思想解题步骤第一步:找到最小规模问题的解。
- 1x1网格:1条路径(向右移动0次,或向下移动0次)

- 1x2网格:1条路径(一直向下移动)
- 1x3网格:1条路径(一直向下移动)
- 1x4网格:1条路径(一直向下移动)
- ....
- 1xn网格:1条路径(一直向下移动)
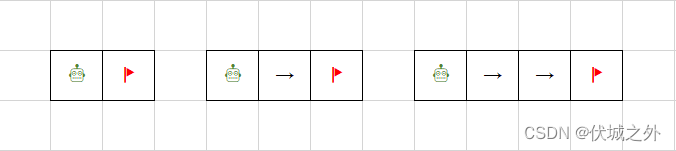
- 2x1网格:1条路径(一直向右移动)
- 3x1网格:1条路径(一直向右移动)
- 4x1网格:1条路径(一直向右移动)
- ......
- nx1网格:1条路径(一直向右移动)
所以可以总结出最小规模解为:
- f(m,1) = 1
- f(1, n) = 1
递归思想解题步骤第二步:分解问题
所谓分解问题,即relate hard case to simple case,那我们就多找几组simple case,观察它们之间的关系

从上面simple case可以发现,
- 2x2网格,可以是2x1网格新增一行,或1x2网格新增一列
- ......
- mxn网格,可以是mx(n-1)网格新增一行,(n-1)xm网格新增一列
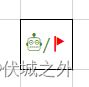
而从mx(n-1)网格,新增一行后,变成mxn网格,网格右下角位置就变了,并且从mx(n-1)网格右下角到mxn网格的右下角只有一种路径(如下图黑旗子到红旗子)
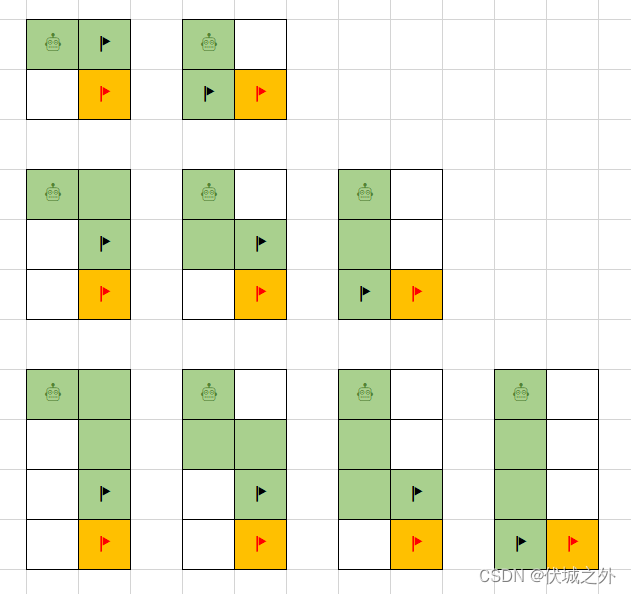
因此 mxn网格的移动路径数 = mx(n-1)网格的移动路径数 + (m-1)xn网格的移动路径数
我们可以总结出分解公式为
f(m,n) = f(m-1, n) + f(m, n-1)
function path(m,n){
if(m===1 || n===1) return 1
return path(m-1, n) + path(m, n-1)
}
当第二步完成后,第三步合并子问题的解,其实就是当递归到出口时,递归回溯的流程。
整数划分
将正整数n表示成一系列正整数之和:n=n1+n2+…+nk,其中n1≥n2≥…≥nk≥1,k≥1。
正整数n的这种表示成为正整数n的划分。求正整数n的不同划分个数。
例如:正整数6有如下11种不同的划分:
- 6
- 5+1
- 4+2
- 4+1+1
- 3+3
- 3+2+1
- 3+1+1+1
- 2+2+2
- 2+2+1+1
- 2+1+1+1+1
- 1+1+1+1+1+1
此题如果采用递归思想来分解问题的话,有两个方向:
- 一是求解 f(n)和f(n-?)之间的关系,比如f(6)=11,f(5) = 7,求f(6)和f(5)之间的关系
- 二是求解 f(n, n1) 和 f(n,nk) 之间的关系(nk表示n分解时最大加数值),比如 f(6,6) = 11, f(6, 5) = 10,求f(6,6) 和 f(6,5) 之间的关系
目前,我们无法判断哪种方向好走,所以我们都走一遍:
推导f(n)和f(n-?)之间的关系
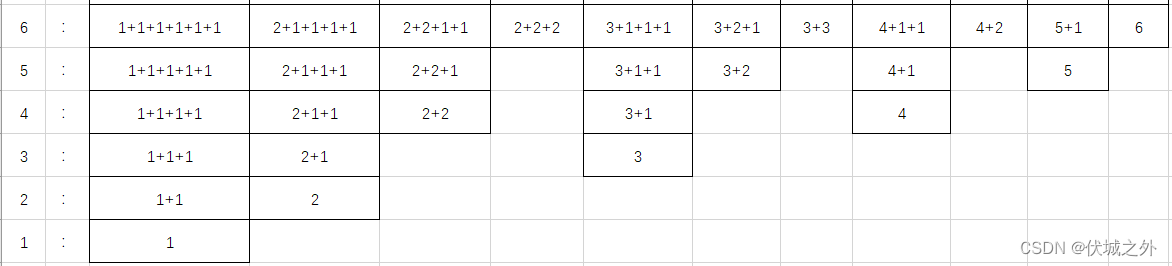
通过查找规律可以得到如下图
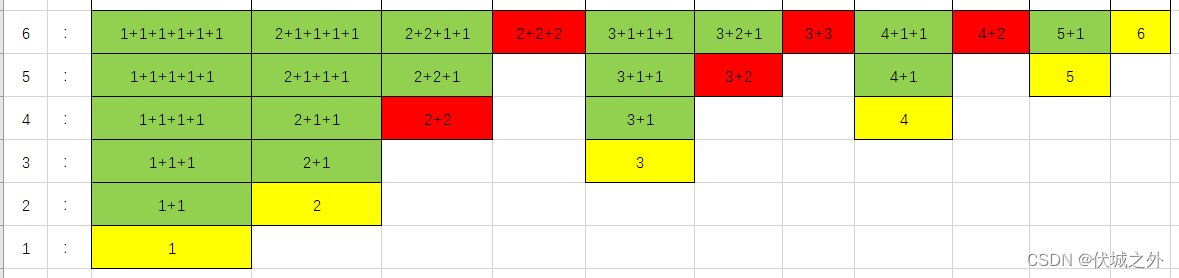
黄色部分划分情况就是n本身,是f(n)必有的一种划分情况。
绿色部分划分情况,其实就是f(n)继承自f(n-1)的划分情况,比如 n=2时,可以划分为 1+1,2,而n=3时,划分的情况就包括了 1+1+1, 2+1 。
如果没有红色部分,则f(n)和f(n-1)具有如下规律:f(n) = f(n-1) + 1
但是,实际划分情况种还是具有红色部分,这些部分也可以看成为继承得来的

比如f(6)种的2开头的划分情况
- 2+1+1+1+1
- 2+2+1+1
- 2+2+2
就是继承自f(4)的1开头和2开头的划分情况
- 1+1+1+1
- 2+1+1
- 2+2
但是上面这种继承规律并不是作用于f(n)的,而是作用于f(n)内部某种划分情况的,所以我们可以推理出,无法直接找到f(n)和f(n-?)之间的关系,或者说要推理出f(n)和f(n-?)之间的关系,则必选推理出f(n)内部各种划分情况的关系。
推导f(n, n1) 和 f(n,nk) 之间的关系
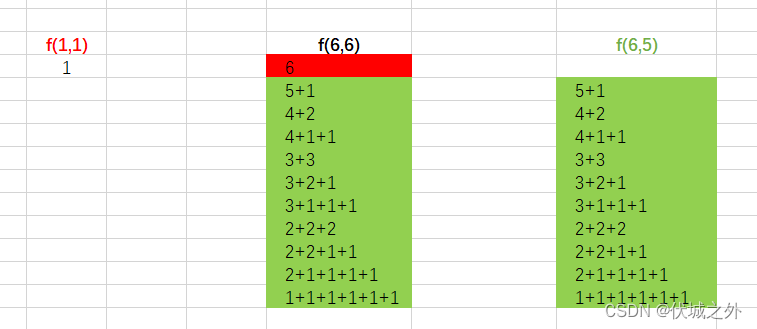
假设正整数n的最大划分加数为m时的划分情况总数为 f(n,m)
则f(n,m)的最小规模解为:
- f(1,m) = 1
- f(n, 1) = 1
接下来求解,f(n,n1)和f(n,nk)之间关系
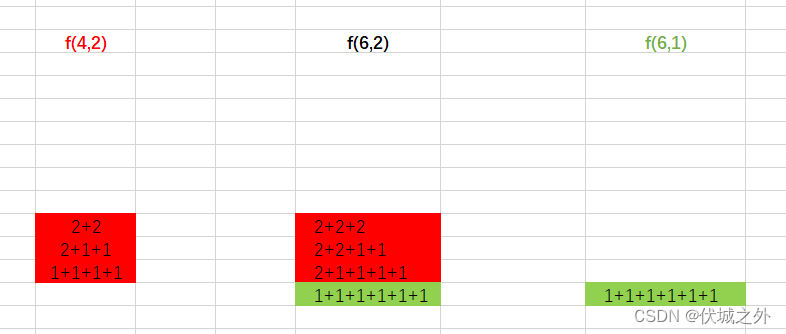

即 f(n,m) = f(n, m-1) + f(n-m, m)
 即 f(n, n) = f(n, n-1) + 1
即 f(n, n) = f(n, n-1) + 1
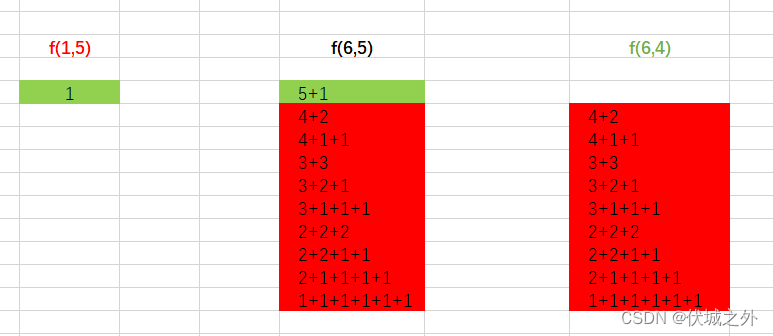
注意,m>n时无意义,此时f(n,m) 等价于 f(n,n),如f(1,5) 等价于 f(1,1)
所以最终递归算法为
- f(1,m) = 1
- f(n, 1) = 1
- f(n, n) = f(n, n-1) + 1
- f(n,m) = f(n, m-1) + f(n-m, n-m)
function divide(n,m) {
if(n===1 || m===1) return 1
if(m>n) return divide(n,n)
if(m===n) return divide(n, n-1) + 1
return divide(n, m-1) + divide(n-m, m)
}通过上面算法,我们就可以得到正整数n,在最大划分加数m时的划分情况总数。
而题目要求,我们总是求解正整数n所有的划分情况,即最大划分加数m=n,因此我们只需要为m设置默认值n即可
function divide(n,m=n) {
if(n===1 || m===1) return 1
if(m>n) return divide(n,n)
if(m===n) return divide(n, n-1) + 1
return divide(n, m-1) + divide(n-m, m)
}
汉诺塔
汉诺塔(Tower of Hanoi),是一个源于印度古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定,在小圆盘上不能放大圆盘,在三根柱子之间一次只能移动一个圆盘。
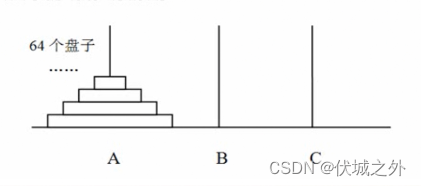
首先,64层黄金圆盘的移动规律我们很难总结出来,但是1层,2层,3层的移动规律却很好总结,所以我们尝试着采用递归思想来将64层大规模的问题,分解为相同的,小规模的问题。
- 当A柱只有1层黄金圆盘时,至少需要移动1次:

- 当A柱有2层黄金圆盘时,至少需要移动3次

- 当A柱有3层黄金圆盘时,至少需要移动7次

好了,我们就模拟最小的三种数据规模的移动情况,因为到了A柱有4层黄金圆盘时,移动起来已经有一定的复杂度了。
首先,
当A柱只有1层黄金圆盘时,可以直接得出移动次数就是1次,没有什么好验证的,我们可以将此情况当成递归的出口条件。
其次,我们需要找到递归公式,即找A柱有2,3层黄金圆盘时的移动规律相似之处:
汉诺塔规则,要求将A柱上的黄金圆盘按照相同的叠放顺序转移到C柱上,并且转移过程中,不能出现“大压小”的现象。因此,我们首先要保证先将A柱上第底层最大的黄金圆盘转移到C柱上,而这样转移前提条件,必须如下图所示:
即要将除了最大黄金圆盘外的其余黄金圆盘全部转移到B柱,然后最大黄金圆盘才能直接从A柱转移到C柱
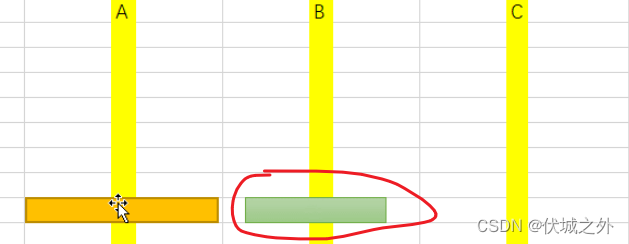

而除了最大黄金圆盘外的其余黄金圆盘转移到B柱的过程也需要满足(大不能压小)规则,所以这个过程可能还需要借助C柱。
当最大的黄金圆盘(第n个黄金圆盘)被移动到C柱后,我们就需要想办法将位于B柱的n-1个黄金圆盘移动到C柱了。
此时,其实我们完全可以忽略处于C柱的最大的黄金圆盘,因为它是最大的,其他任意黄金圆盘移动到它上面,都不会触发“大压小”限制,同时它的移动目的已经达到,不需要再次移动了。
所以,此时完全可以将原始的n层黄金圆盘从A=>C移动,简化为n-1层黄金圆盘从B=>C移动。
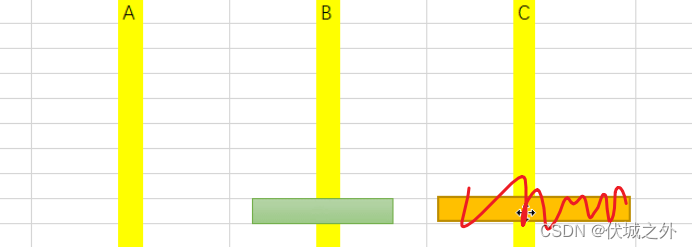
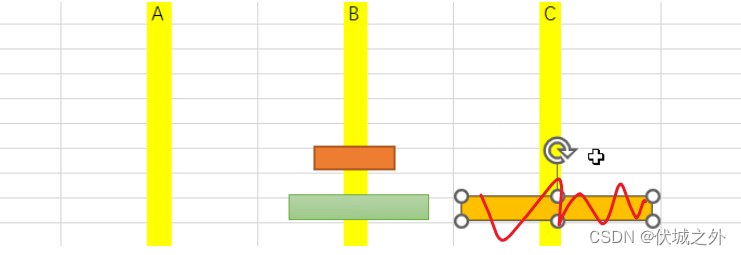
当然,n-1层黄金圆盘从B=>C的移动的过程也可能需要借助A来避免出现“大压小”现象。
根据以上的分析,我们可以写出如下递归算法
/* JavaScript Node ACM模式 控制台输入获取 */
const readline = require("readline");
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout,
});
rl.on("line", (line) => {
console.log(`${line}层汉诺塔,至少需要移动${fn()(parseInt(line))}次`);
});
/* 汉诺塔算法 */
function fn() {
// 移动统计
let steps = [];
// from是黄金圆盘所处的起始柱,to是黄金圆盘需要移向的目标柱,aux是黄金圆盘移动过程中受到“大不压小”限制时被迫临时停放的辅助柱
function hanoi(n, from = "A", aux = "B", to = "C") {
if (n === 0) {
return 0;
}
// 当n=1时,表示起始柱上只有一个黄金圆盘,此时可以直接将黄金圆盘从起始柱移动到目标柱
if (n === 1) {
move(n, from, to);
} else {
// 当n!=1时,表示起始柱上有多个黄金圆盘,此时为了让最大的黄金圆盘n可以移动到目标柱,我们需要将它上面的n-1个黄金圆盘全部移动到辅助柱上临时停放,注意此时对于这n-1个黄金圆盘而言,外层hanoi的辅助柱就是当前hanoi的目标柱,外层hanoi的目标柱就是当前hanoi的辅助柱。
hanoi(n - 1, from, to, aux);
// 由于上一步已经将n-1个黄金圆盘移动到了外层hanoi的辅助柱上,所以黄金圆盘n可以直接移动到外层hanoi的目标柱
move(n, from, to);
// 当黄金圆盘n移动到外层hanoi的目标柱后,我们就可以着手处于外层hanoi的辅助柱上的n-1个黄金圆盘移动到外层hanoi的目标柱了,此时对于这n-1个黄金圆盘而言,外层hanoi的辅助柱就是当前hanoi的的起始柱,外层hanoi的起始柱就是当前hanoi的的辅助柱,目标柱不变。
hanoi(n - 1, aux, from, to);
}
return steps.length;
}
// 移动步骤统计
function move(n, from, to) {
steps.push(`${n}:${from}=>${to}`);
}
return hanoi;
}通过运行上面程序,我们可以发现一个有意思的现象

n层汉诺塔(n>0),至少需要移动2^n - 1次
所以,如果仅需要求解n层汉诺塔最少移动次数,则可以改进算法为:
/* JavaScript Node ACM模式 控制台输入获取 */
const readline = require("readline");
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout,
});
rl.on("line", (line) => {
console.log(`${line}层汉诺塔,至少需要移动${hanoi(parseInt(line))}次`);
});
/* 汉诺塔算法 */
function hanoi(n) {
return (1 << n) - 1;
}
递归算法的弊端
递归深度过大导致的栈内存溢出
fibnaci数列的第一个和第二个数为1,第三个开始的数的值为其前两个fibnaci数的和,请求第100000个fibnaci数。
这道题的算法设计,依然是用递归算法最容易。因为题目要求给出第n个fibnaci数,则说明fibnaci数列中的每一个数都是一个事物,而事物与事物之间的关系,题目已经明确给出:
- f(1) = 1 // 第一个fibnaci数为1
- f(2) = 1 // 第一个fibnaci数为1
- f(n) = f(n-1) + f(n-2); n>2 // 第三个开始的fibnaci数的值为其前两个fibnaci数的和
所以这里我们可以直接给出fibnaci数的求解算法
/* JavaScript Node ACM模式 控制台输入获取 */
const readline = require("readline");
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout,
});
rl.on("line", (line) => {
console.log(fibnaci(parseInt(line)));
});
/* fibnaci数求解 */
function fibnaci(n) {
if (n === 1 || n === 2) return 1;
return fibnaci(n - 1) + fibnaci(n - 2);
}
我们用上面算法求解第十万个fibnaci数看看
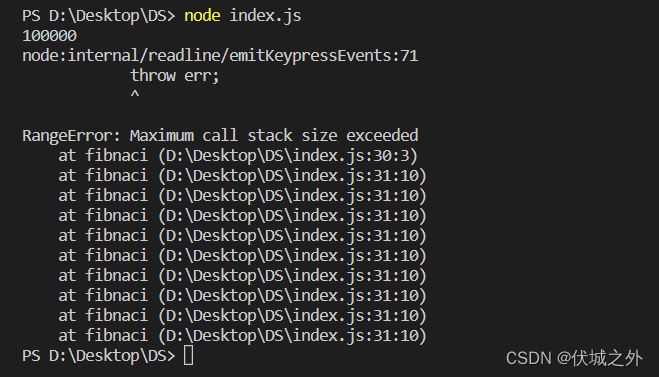
我擦,栈内存溢出!!!
但是我的递归出口和递归方向都没有问题啊!!
这是为什么呢?
原因是,递归深度过大了,超出了栈内存大小了。
我们知道函数调用就会产生函数执行上下文(栈帧),并推入执行栈(栈内存),因此每次函数调用都会占用一点栈内存,而只有函数调用结束,对应函数执行上下文(栈帧)才会出栈,归还占用的栈内存。
而每个递归函数调用,也会占用一点栈内存,但是外层的递归函数必须要等内层的递归函数返回结果,才能结束自身调用,归还占用的栈内存。
如果递归深度过大,则栈内存将一直处于”只借不还“的境地,最终栈内存会被”借完“,导致无内存再分配给新的递归调用。
此时大家可以借鉴我的另一篇博客,来解决递归过深导致的栈溢出问题有趣-如何解决递归过多导致的栈溢出_伏城之外的博客-CSDN博客_递归栈溢出解决方法
子问题交集过多,导致的重复递归
我们还是用fibnaci数求解算法来演示这个问题
fibnaci数求解算法如下
function fibnaci(n) {
if (n === 1 || n === 2) return 1;
return fibnaci(n - 1) + fibnaci(n - 2);
}上面这段代码执行过程可以转为二叉树图示,比如求解fibnaci(6)

其中蓝色箭头是函数调用流程。
可以发现,其中存在大量重复的函数调用,比如
- f(1)被重复调用了3次
- f(2)被重复调用了5次
- f(3)被重复调用了3次
- f(4)被重复调用了2次
当n的值越大,产生的重复函数调用就越多,且这个重复调用的函数增长率是非线性的,每当n++,则增长2^(n-1)+1次重复函数调用。
每次函数调用都会占用时间和内存,所以重复的递归调用不仅是无意义的,也是极其浪费性能的。
为了解决函数重复调用的问题,我们需要建立一张缓存表,来缓存已经求得的fibnaci数。并且每次获取fibnaci数时,必须先去缓存表中查找,如果没有再进行递归。
/* JavaScript Node ACM模式 控制台输入获取 */
const readline = require("readline");
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout,
});
rl.on("line", (line) => {
console.log(fn()(parseInt(line)));
});
/* fibnaci数求解 */
function fn() {
const cache = {};
function fibnaci(n) {
if (cache[n]) return cache[n];
if (n === 1 || n === 2) {
cache[n] = 1;
} else {
cache[n] = fibnaci(n - 1) + fibnaci(n - 2);
}
return cache[n];
}
return fibnaci;
}
此时,fibnaci递归算法的性能将大大提升。
我们再来看此时的函数调用流程图
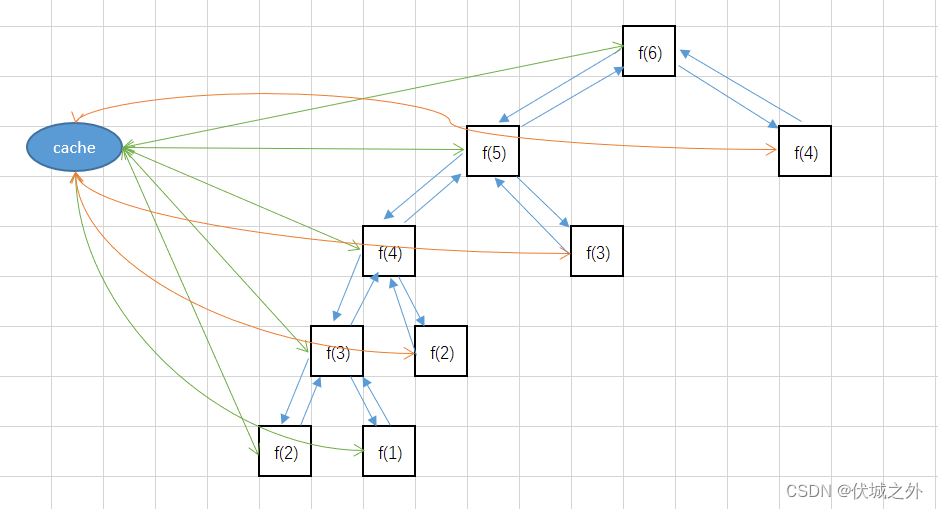
其中绿色和橙色是双向箭头线,代表从cache中获取或向cache存入fibnaci数。
绿色双向箭头线,获取失败,存入成功。
橙色双向箭头线,获取成功,无需存入。
这样一来,就可以减少部分重复的递归调用了。
但是我们发现,依旧存在部分重复的函数调用,虽然此时重复的函数调用的逻辑大大简化,直接从cache中获取结果,但是函数调用的框架任然是冗余的。
所以,对于问题分解出现交叉子问题时,递归算法并不是最佳选择。
自顶向下的递归和自底向上的递推
我们通过上一个例子中图示可以发现,递归算法其实是自顶向下的,即f(6)向下分解为f(5)、f(4)、f(5)向下分解为f(4)、f(3),......,直到底部f(2)、f(1)。
自顶向下的递归流程必然伴随着反向的递归回溯流程,而目前变成语言中,只有函数可以完成递归回溯,因此前面递归算法的优化中,始终无法彻底优化掉所有重复递归函数的调用,只能优化掉部分重复的函数调用,其余重复调用也仅能优化函数内部取值逻辑。
因此,想要彻底解决问题分解产生交叉子问题引起的重复递归调用问题,只能放弃自顶向下的递归算法,改用自底向上的递推。
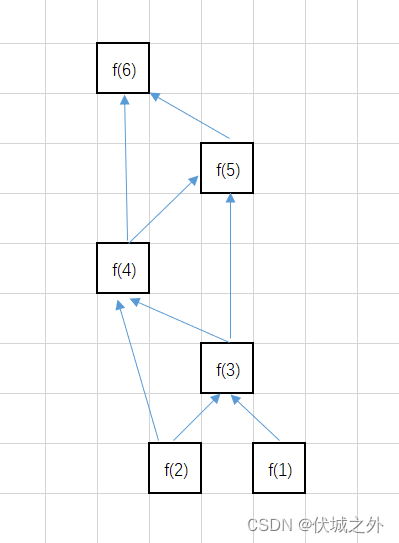
其算法如下
/* JavaScript Node ACM模式 控制台输入获取 */
const readline = require("readline");
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout,
});
rl.on("line", (line) => {
console.log(fn()(parseInt(line)));
});
/* fibnaci数求解 */
function fn() {
const cache = [];
function fibnaci(n) {
cache[1] = 1;
cache[2] = 1;
for (let i = 3; i <= n; i++) {
cache[i] = cache[i - 1] + cache[i - 2];
}
return cache[n];
}
return fibnaci;
}
这种自底向上的递推算法,其实就是动态规划。它的时间复杂度为O(n)。
后面有时间会写一个博客详细总结下动态规划。
相关文章
- 八皇后问题递归算法思想_迷宫在数据结构中的地位
- JS算法探险之数组
- 递归算法时间复杂度分析[通俗易懂]
- 图灵奖第一位获得者:艾伦•佩利——算法的综合
- 【数据结构与算法】深入浅出递归和迭代的通用转换思想[通俗易懂]
- 最长上升子序列 LIS算法实现[通俗易懂]
- java中的递归算法_java递归算法详解
- OpenSSL密码库算法笔记——第5.2章 椭圆曲线算法的函数架构图
- js三目运算符多条表达式_递归算法js
- 二叉树中序遍历(非递归)算法实现–C语言「建议收藏」
- 使用Vue3实现【羊了个羊】的算法方面全面解析!
- 汉罗塔编程_c语言斐波那契数列递归算法
- 经典递归解决汉诺塔_c语言汉诺塔递归算法
- js斐波那契数列递归算法_php斐波那契数列递归算法
- 指派问题匈牙利算法例题_匈牙利算法matlab代码
- 推荐系统[八]算法实践总结V2:排序学习框架(特征提取标签获取方式)以及京东推荐算法精排技术实战
- 七日算法先导(四)—— 快速排序,插入排序
- 【二】MADDPG多智能体算法实现(parl)【追逐游戏复现】
- 关于递归算法的优化Ⅰ(以经典的斐波那契数列为例)
- 通用量子算法:量子相位估计算法
- 【计算机网络】网络层 : OSPF 协议 ( 协议简介 | 链路状态路由算法 | OSPF 区域 | OSPF 特点 )
- 【算法】递归算法 ② ( 使用递归实现二分法 | if else 编码优化 )
- Mysql Innodb存储引擎之索引与算法
- Java实现的二分查找算法详解编程语言
- Java数据结构和算法(八)——递归详解编程语言
- 算法-把二叉树打印成多行详解编程语言
- 书评:《算法之美( Algorithms to Live By )》
- php全排列递归算法代码
- 全排列算法的非递归实现与递归实现的方法(C++)
- 二叉树前序遍历的非递归算法
- javascript随机之洗牌算法深入分析
- C#递归实现回文判断算法

