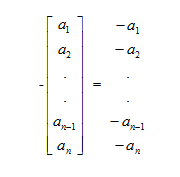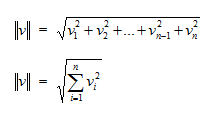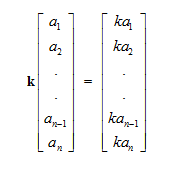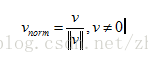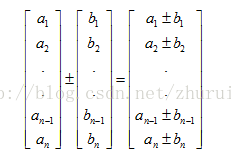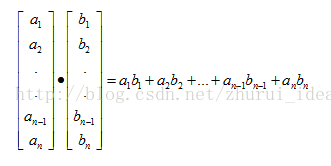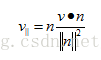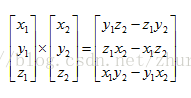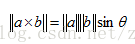3D数学读书笔记——向量运算及在c++上的实现

 本系列文章由birdlove1987编写。转载请注明出处。

 文章链接： http://blog.csdn.net/zhurui_idea/article/details/24782661

開始之前：接上上篇说的，张宇老师说过线性代数研究的就是向量。事实上严谨的说，数学中专门研究向量的分之称作线性代数，线性代数是一个很有趣而且应用广泛的研究

领域，但它与3D数学关注的领域并不同样。3D数学主要关心向量和向量运算的几何意义。

零向量：不论什么集合，都存在 the additive identity element。我们把它表示为 x (变量仅仅是作为代表未知量的占位符存在) ，对集合中随意元素 y ，满足 y + x = y。

n维向量集合的 the additive identity element 就是 n维零向量。

它的每一维都是零。

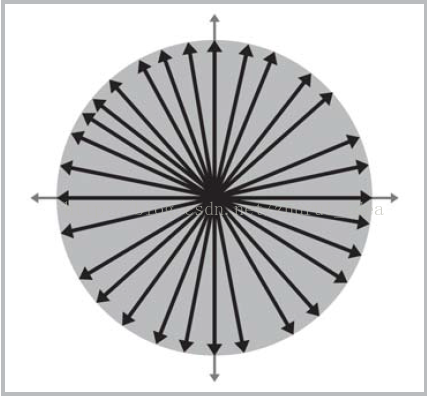
零向量很特殊。由于它是唯一大小为零的向量。对于其它随意数m，存在无数多个大小为m的向量。

它们构成了一个圆。

零向量也是唯一一个没有方向的向量。事实上零向量表示的就是“没有位移”，就像标量零表示“没有数量”一样。

负向量：对于随意集合，元素 x 的加性逆元为 -x，其与x相加等于the additive identity，即 x + (-x) = 0.             

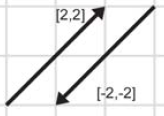
运算法则1：向量变负。要得到随意维向量的负向量，仅仅须要简单的将向量地每个分量都变负就可以。

几何解释：向量变负，将得到一个和原来向量大小相等。方向相反的向量。（向量在图中的位置是无关紧要的。仅仅有大小和方向才是最重要的）。

向量大小：事实上向量的大小和方向都没有在向量的数学表示中明白的表示出来。全部向量的大小是须要计算的，向量的大小也常被称作向量的长度或模。

运算法则2：n维向量大小的计算公式例如以下图

线性代数中，向量的大小用向量两边双竖线表示，这和标量的绝对值在标量两边加单竖线表示类似。（和我们在神经网络课上学的范数也很像）。

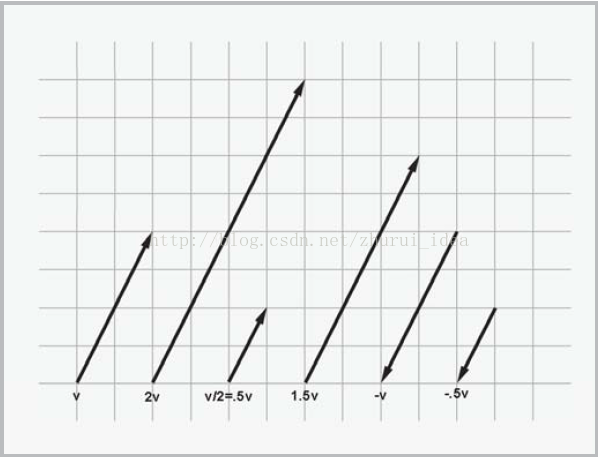
标量与向量的乘法：尽管标量与向量不能相加。但它们能相乘。

结果得到一个向量，与源向量平行。但长度不同或方向相反。

运算法则3：标量和向量的乘法很直接，将向量的每个分量都与标量相乘就可以。

ps：1. 标量与向量的乘法和除法优先级高于加法和减法。

    2. 标量不能除以向量，而且向量不能除以还有一个向量。

    3. 负向量能被觉得是乘法的特殊情况。乘以标量-1.

几何解释：几何意义上，向量乘以标量K的效果是以因子|k| 缩放向量的长度。

标准化向量：对很多向量，我们仅仅关心它的方向而不关心其大小，这种情况下，使用单位向量将很方便。

单位向量就是大小为1的向量，单位向量常常也被称作标准化向量。

运算法则4：对于随意非零向量v，都能计算出一个和v方向同样的单位向量 v‘ 这个过程被称作向量的标准化，要标准化向量，将向量除以它的大小就可以。

ps：零向量不能被标准化。数学上这是不同意的，由于将导致除零。几何上也没有意义，由于零向量没用方向。

向量的加法和减法：假设两个向量的维数同样，那么它们能相加，或相减。

结果向量的维数与原向量同样。

向量加减法的记法和标量加减的记法同样。

运算法则5：两个向量相加或相减，将相应分量相加就可以。

ps：（1）向量不能与标量或维数不同的向量相加减。

    （2）和标量加法一样，向量加法满足交换律，但向量减法不满足交换律。

向量点乘：向量点乘也常称作向量内积。

运算法则6：向量点乘就是相应分量乘积的和。结果是一个标量。

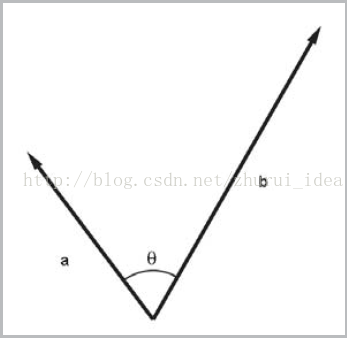
几何解释：点乘结果描写叙述了两个向量的“类似”程度，点乘结果越大，两个向量越相近。

ps：（1）假设a，b中随意一个为零。那么a·b的结果也等于零。可是点乘等于零也可能是两个向量相互垂直。

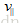
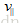
向量投影：给定两个向量 v 和 n，能将v分解成两个分量：和。它们分别平行和垂直于n 。并满足 v = +。一般称平行分量为 v 在 n 上的投影。

运算法则7：我们使用点乘计算投影。

向量叉乘：向量叉乘又叫叉积。仅可应用于3D向量。

运算法则8：                       

几何解释：叉乘得到的向量垂直于原来的两个向量。

========================华丽的切割线===============================

以下用c++代码实现以下上面出现过的计算过程：

class Vector3D {
public:
float x,y,z;
// 构造函数
// 默认构造函数。不运行不论什么操作
Vector3D() {}
// 复制构造函数
Vector3D(const Vector3D &a) : x(a.x), y(a.y), z(a.z) {}
// 带三个參数的构造函数，三个值完毕初始化
Vector3D(float nx, float ny, float nz) : x(nx), y(ny), z(nz) {}
// 重载赋值运算符
Vector3D &operator =(const Vector3D &a) {
  x = a.x; y = a.y; z = a.z;
  return *this;
}
// 重载比較运算符
bool operator ==(const Vector3D &a) const {
  return x==a.x && y==a.y && z==a.z;
}
bool operator !=(const Vector3D &a) const {
  return x!=a.x || y!=a.y || z!=a.z;
}
// 向量运算
// 设置零向量
void zero() { x = y = z = 0.0f; }
// 重载负运算符
Vector3D operator –() const { return Vector3D(–x,–y,–z); }
// 重载加减运算符
Vector3D operator +(const Vector3D &a) const {
  return Vector3D(x + a.x, y + a.y, z + a.z);
}
Vector3D operator –(const Vector3D &a) const {
  return Vector3D(x – a.x, y – a.y, z – a.z);
}
// 重载标量乘、除法运算符
Vector3D operator *(float a) const {
  return Vector3D(x*a, y*a, z*a);
}
Vector3D operator /(float a) const {
  float oneOverA = 1.0f / a; // 没有对除零检查
  return Vector3D(x*oneOverA, y*oneOverA, z*oneOverA);
}
// 重载？=运算符
Vector3D &operator +=(const Vector3D &a) {
  x += a.x; y += a.y; z += a.z;
  return *this;
}
Vector3D &operator –=(const Vector3D &a) {
  x –= a.x; y –= a.y; z –= a.z;
  return *this;
}
Vector3D &operator *=(float a) {
  x *= a; y *= a; z *= a;
  return *this;
}
Vector3D &operator /=(float a) {
  float oneOverA = 1.0f / a;
  x *= oneOverA; y *= oneOverA; z *= oneOverA;
  return *this;
}
// 向量标准化
void normalize() {
  float magSq = x*x + y*y + z*z;
  if (magSq > 0.0f) { // 检查除零
     float oneOverMag = 1.0f / sqrt(magSq);
    x *= oneOverMag;
    y *= oneOverMag;
    z *= oneOverMag;
}
}
// 向量点乘。重载乘法运算符
float operator *(const Vector3D &a) const {
  return x*a.x + y*a.y + z*a.z;
}
};

// 求向量模
inline float vectorMag(const Vector3D &a) {
  return sqrt(a.x*a.x + a.y*a.y + a.z*a.z);
}
// 计算两向量的叉乘
inline Vector3D crossProduct(const Vector3D &a, const Vector3D &b) {
  return Vector3D(a.y*b.z – a.z*b.y,a.z*b.x – a.x*b.z,a.x*b.y – a.y*b.x);
}
// 标量乘法
inline Vector3D operator *(float k, const Vector3D &v) {
  return Vector3D(k*v.x, k*v.y, k*v.z);
}
// 计算两点间距离
inline float distance(const Vector3D &a, const Vector3D &b) {
  float dx = a.x – b.x;
  float dy = a.y – b.y;
  float dz = a.z – b.z;
  return sqrt(dx*dx + dy*dy + dz*dz);
}

// 全局零向量
extern const Vector3D kZeroVector;

                                                             -End-

 參考文献：（1）《3D Math Primer for Graphics and Game Development》

                 （2）百度百科