从主成分分析到发育网络的核心算法CCIPCA-CCILCA

在写《特征学习：学习之海中的遗珠》过程中，发现内容太多，已经超过单篇博客的承载能力，另外里面几个内容都有各自己额外的主题。因此，本人将《特征学习：学习之海中的遗珠》第二节（介绍几个经典的特征学习方法）中能够独立成篇的3个小节单独提出形成三篇对应的博客。本篇对应第1小节：从主成分分析到发育网络的核心算法。

1.写在前面

PCA可以用来解决的问题【Andrew Ng曾在讲PCA时提到过】：

1）减少数据因为存储而造成的内存和硬盘的占用；
2）加速训练过程；
3）高维数据可视化。

值得注意的是： PCA并没有把握一定能提高后续机器学习任务的效果，也没有把握能够防止过拟合问题。

主成分分析（Principal Component Analysis,简称PCA） 提供了一种用低维数据来表示高维复杂数据最主要特征的途径。PCA的思想是将$m$维特征映射到$k$维空间上$k<m$，这$k$维特征是全新的正交特征，最新构造出来的$k$维特征，而不是简单地从$m$维特征中去除其余$m-k$维特征。博客主成分分析|PCA算法大全罗列了大部分现有的PCA类算法，包括：针对 非线性数据的KPCA，针对二维图片数据的2DPCA/2D2DPCA以及BDPCA等。此处只介绍原始PCA算法以及它的一个增量式版本——CCIPCA，然后介绍翁巨扬教授提出的发育网络（Developmental Network,简称DN） 中的核心算法增量式叶成分分析(CCILCA)。各部分都可展开成原理、算法推导、示例代码、结果分析四个部分。

本文并非单纯为了罗列方法，驱动我总结这篇博客的原因是主成分分析与发育网络的关系。CCILCA作为发育网络的核心算法，根据新到来的数据对网络的节点进行更新，其中每个节点的更新算法就是一个CCIPCA。也就是说发育网络的核心原理之一竟然是主成分分析（另外一个是赫布学习理论）。CCIPCA与CCILCA的关系会在第四部分进行时详细介绍。

2. 主成分分析(PCA）算法与应用

2.1 原理

PCA可以被定义为数据在低维线性空间上的正交投影，这个线性空间被称为主子空间（principal subspace），使得投影数据的方差被最大化（Hotelling, 1933），即最大方差理论。等价地，它也可以被定义为使得平均投影代价最小的线性投影，即最小误差理论。平均投影代价是指数据点和它们的投影之间的平均平方距离（Pearson, 1901）。从最大方差理论与最小误差理论来推导PCA，最终的结果是一样的。对于数据集 X = { x 1 , x 2 , . . . x n } \mathbf{X}=\{\mathbf{x}_1, \mathbf{x}_2, ...\mathbf{x}_n\} X={x1​,x2​,...xn​}，我们以最大方差理论为例来推导PCA：

在信号处理中，认为信号具有较大的方差，噪声有较小的方差，信噪比就是信号与噪声的方差比，越大越好。因此我们认为，最好的k维特征是将m维样本点变换为k后，每一维上的样本方差都尽可能的大。

2.2 算法推导

首先，考虑在一维空间$(k=1)$上的投影。我们可以使用$m$维向量$\mathbf{w}$定义这个空间的方向。为了方便并不失一般性，我们假定选择一个单位向量，从而${\mathbf{w}}^T\mathbf{w}=1$。

(假设数据是零均值化后的)

如上图所示，红色点表示原样本点${\mathbf{u}}^{(i)}$，$\mathbf{w}$是蓝色直线的斜率也是直线的方向向量，而且是单位向量，直线上蓝色点表示原样本点${\mathbf{u}}^{(i)}$在$\mathbf{w}$上的投影。容易知道投影点离原点的距离是${\mathbf{u}}^{(i)T}\mathbf{w}$,由于这些原始样本点的每一维特征均值都为0，因此投影到$\mathbf{w}$上的样本点的均值仍然是0。

假设原始数据集为$\mathbf{X}\in {\mathbb{R}}^{m\times n}$，我们的目标是找到最佳的投影空间$\mathbf{W}=[{\mathbf{w}}_1,{\mathbf{w}}_2,...,{\mathbf{w}}_k]\in {\mathbb{R}}^{n\times k}$，其中${\mathbf{w}}_i$是单位向量且${\mathbf{w}}_i$是单位向量且${\mathbf{w}}_i$与${\mathbf{w}}_j(i\ne j)$正交，何为最佳的$\mathbf{W}$？就是原始样本点投影到$W$上之后，使得投影后的样本点方差最大。

我们先将原始数据集$\mathbf{X}$零均值化为 U = { u 1 , u 2 , . . . , u n } \mathbf{U}=\{\mathbf{u_1}, \mathbf{u_2}, ..., \mathbf{u_n}\} U={u1​,u2​,...,un​},其中，${\mathbf{u}}_{\mathbf{i}}={\mathbf{x}}_{\mathbf{i}}-{\sum }_{j=1}^n{\mathbf{x}}_{\mathbf{j}}$。

由于投影后均值为$0$，因此数据集$\mathbf{U}$沿某一单位向量$\mathbf{w}$投影后的总方差为：
$$\frac{1}{n}\sum _{i=1}^n({\mathbf{u}}_i^T\mathbf{w}{)}^2=\frac{1}{n}\sum _{i=1}^n{\mathbf{w}}^T{\mathbf{u}}_i{\mathbf{u}}_i^T\mathbf{w}={\mathbf{w}}^T\left[\frac{1}{n}\sum _{i=1}^n{\mathbf{u}}_i{\mathbf{u}}_i^T\right]\mathbf{w}$$

其中$\frac{1}{n}{\sum }_{i=1}^n{\mathbf{u}}_i{\mathbf{u}}_i^T=\frac{1}{n}{\sum }_{i=1}^n({\mathbf{x}}_i-{\sum }_{j=1}^n{\mathbf{x}}_j)({\mathbf{x}}_i-{\sum }_{j=1}^n{\mathbf{x}}_j{)}^T$就是原始数据集$\mathbf{X}$的协方差矩阵（因为无偏估计的原因，一般协方差矩阵除以$n-1$，这是用$n$）。

$$\lambda ={\mathbf{w}}^T\mathbf{\Sigma }\mathbf{w}$$
其中，$\lambda =\frac{1}{n}{\sum }_{i=1}^n({\mathbf{x}}_i^T\mathbf{w}{)}^2,\mathbf{\Sigma }=\frac{1}{n}{\sum }_{i=1}^n{\mathbf{x}}_i{\mathbf{x}}_i^T$。

上式两边同时左乘$\mathbf{w}$，注意到$\mathbf{w}{\mathbf{w}}^T=1$（单位向量），则有

$$\lambda \mathbf{w}=\mathbf{\Sigma }\mathbf{w}$$
所以$\mathbf{w}$是矩阵$\mathbf{\Sigma }$的特征值所对应的特征向量。

欲使投影后的总方差最大，即$\lambda$最大， 可知最佳的投影向量$w$是特征值$\lambda$最大时对应的特征向量，因此，当我们将$w$设置为与具有最大的特征值向量相等时，方差会达到最大值。这个特征向量被称为第一主成分。

PCA算法如下图所示：

2.3 示例程序

from sklearn.decomposition import PCA
from sklearn.datasets import load_digits #8x8的手写数字数据
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import train_test_split
 
import time
 
X, y = load_digits(return_X_y=True)
print('X shape:', X.shape)  # 此处会看到X是64维的数据
X_train, x_test, y_train, y_test = train_test_split(X, y)
 
 
tic = time.time()
knn_clf = KNeighborsClassifier()
knn_clf.fit(X_train, y_train)
print (knn_clf.score(x_test, y_test))
toc = time.time()
print ('Time of method[exec_without_pca] costs:'+str(toc-tic)) 
 
print ('----' * 10)
tic = time.time()
knn_clf = KNeighborsClassifier()
pca = PCA(n_components=0.95) # 重构阈值为95%
pca.fit(X_train, y_train)
X_train_dunction = pca.transform(X_train)
X_test_dunction = pca.transform(x_test)
knn_clf.fit(X_train_dunction, y_train)
print (knn_clf.score(X_test_dunction, y_test))
toc = time.time()
print ('Time of method[exec_with_pca] costs:'+str(toc-tic)) 

import matplotlib.pyplot as plt
%matplotlib inline
def draw_graph():
    pca = PCA(n_components=2)
    pca.fit(X)
    X_reduction = pca.transform(X)
    for i in range(10):
        plt.scatter(X_reduction[y==i,0], X_reduction[y==i,1], alpha=0.8, label='%s' % i)
    plt.legend()
    plt.show()

输出：

降维数据可视化结果：’

其它数据显示：
经过PCA降维后，发现降到28维（原始维数为64维）后，就能达到95%数据重构精度。

>>print(len(pca.components_))
28
>>print(pca.explained_variance_ratio_)
[0.14797442 0.13659413 0.11802823 0.08412275 0.05932165 0.05048908
 0.04237307 0.0355668  0.0334889  0.03029803 0.02443289 0.02229051
 0.01804256 0.01782603 0.01516046 0.01396237 0.013309   0.01217414
 0.01043489 0.00897301 0.00880779 0.00771099 0.00760128 0.00726781
 0.00689468 0.00609627 0.00579926 0.00505733]

将这前28特征向量打印出来：

A = pca.components_
print(pca.explained_variance_ratio_)
import matplotlib.pyplot as plt
%matplotlib inline
fig = plt.figure(figsize=(12, 8))
for i in range(len(A)):
    fig.add_subplot(4, 7, i+1)
    plt.title(i+1)
    plt.imshow(A[i].reshape((8,8)))
    plt.xticks([])
    plt.yticks([])
    plt.axis("off")
plt.show()

2.4 结果分析

以上示例与结果表明，数据经PCA降维后的准确率没有明显提高。但是经过PCA降维后，用于训练的数据维度变少了，因此计算成本明显降低了。并且，在原始高维空间中揉杂在一起，不可分的数据，利用PCA降维的低维空间中，数据也还是揉杂在一起的。

3 增量式PCA（CCIPCA）算法与应用

candid covariance-free incremental principle component analysis直接协方差无关的增量式主成分分析,简称CCIPCA

考虑到很多实际应用无法一次性收集足够的训练数据，更普遍的情况是：数据是随着时间不断产生的，按序列依次输入到学习系统中。要应对这种情况，算法必需能够具备仅仅依靠已经学到的知识与新接受到的数据进行增量式的学习。明显地，原始PCA算法无法应对这种情况，本节介绍的CCIPCA是对原始PCA的改进，它能够只依赖当前的新数据进行学习降维模型。

3.1 算法推导

上一节根据最大方差理论推导PCA过程中，可得数据集$\mathbf{X}$沿某一单位向量$\mathbf{w}$投影后的总方差$\mathbf{\Sigma }(n)$为：
$${\mathbf{\Sigma }}_n=\frac{1}{n}\sum _{i=1}^n({\mathbf{x}}_i-{\mathbf{m}}_n)({\mathbf{x}}_i-{\mathbf{m}}_n{)}^T=\frac{1}{n}\sum _{i=1}^n{\mathbf{u}}_i{\mathbf{u}}_i^T\text{\hspace{1em}(1)}$$

其中${\mathbf{m}}_n=\frac{1}{n}{\sum }_{i=1}^n{\mathbf{x}}_i$就是原始数据集$\mathbf{X}$的协方差矩阵（因为${\mathbf{x}}_i$的均值为$0$，因为无偏估计的原因，一般协方差矩阵除以$n-1$，这是用n）。

第$i$个特征值和特征向量的计算公式为${\lambda }_{in}{\mathbf{w}}_{in}={\mathbf{\Sigma }}_n{\mathbf{w}}_{in}$,其中${\mathbf{w}}_{in}$为第$n$输入时待求的第$i$个特征向量，${\lambda }_{in}$为对应的特征值 。CCIPCA算法为了加快迭代的速度，整个迭代是对特征值和特征向量的乘积${\lambda }_{in}{\mathbf{w}}_{in}$进行的，设第$n$个输入时有

$${\mathbf{v}}_{in}={\lambda }_{in}{\mathbf{w}}_{in}={\mathbf{\Sigma }}_n{\mathbf{w}}_{in}\text{\hspace{1em}(2)}$$

把（1）式代入（2）式，可得
$${\mathbf{v}}_{in}=\frac{1}{n}\sum _{j=1}^n{\mathbf{u}}_j{\mathbf{u}}_j^T{\mathbf{w}}_{in}\text{\hspace{1em}(3)}$$

若通过迭代获得特征值和特征向量的乘积${\mathbf{v}}_{in}$，因特征向量是归一的，只要对（2）式求模（内积，开根），可求得${\lambda }_{in}=||{\mathbf{v}}_{in}||,{\mathbf{w}}_{in}=\frac{{\mathbf{v}}_{in}}{||{\mathbf{v}}_{in}||}$。

迭代采用（3）式，把$\frac{{\mathbf{v}}_{i,n-1}}{||{\mathbf{v}}_{i,n-1})||}$近似为${\mathbf{w}}_{in}$代入（3）式，经变换可得CCIPCA的基本迭代公式:

$${\mathbf{v}}_{in}=\frac{n-1}{n}{\mathbf{v}}_{i,n-1}+\frac{1}{n}{\mathbf{u}}_n{\mathbf{u}}_n^T\frac{{\mathbf{v}}_{i,n-1}}{||{\mathbf{v}}_{i,n-1}||}\text{\hspace{1em}(4)}$$

其中,$\frac{n-1}{n}$为上一步的迭代值 ${\mathbf{v}}_{i,n-1}$的权值，第2项的$\frac{1}{n}$相当于迭代的调整步长。

${\mathbf{u}}_n={\mathbf{x}}_n-{\mathbf{m}}_n$作为第$n$个新输入数据对迭代向量${\mathbf{v}}_{in}$的调整，在迭代中${\mathbf{v}}_{in}$逐步收敛到所求的第$i$个特征向量。

对不同序号的向量${\mathbf{v}}_i$，都可以用（4）式迭代，只是输入的向量${\mathbf{u}}_n$不同。求最大的特征值对应的特征向量时，${\mathbf{u}}_n$为机器人采到的第$n$个均值化的数据。在求第2，第3乃至更后面的特征向量时，须作以下处理：

已经通过迭代得到第1个特征向量，先设${\mathbf{u}}_{1n}={\mathbf{u}}_n$，并把${\mathbf{u}}_{1n}$投影到上一个已经求到的特征向量上（现为第1个特征向量），求出残差数据${\mathbf{u}}_{2n}$，如下式表示:
$${\mathbf{u}}_{2n}={\mathbf{u}}_{1n}-{\mathbf{u}}_{1n}^T\frac{{\mathbf{v}}_{1n}}{||{\mathbf{v}}_{1n}||}\frac{{\mathbf{v}}_{1n}}{||{\mathbf{v}}_{1n}||}$$

${\mathbf{u}}_{2n}$作为求第2个特征向量的输入，类似的可求出第3，第4，…个特征向量。因残差数据和上1个特征向量所恢复的数据正交，从而可求出所有相互正交的特征向量。另外，每输入1个新的数据时，均值也要更新，对（1）式，输入第$n$个数据时的均值 采用如下迭代式，$${\mathbf{m}}_n=\frac{n-1}{n}{\mathbf{m}}_{n-1}+\frac{1}{n}{\mathbf{u}}_n^T$$

注意：最终的特征向量${\mathbf{w}}_i=\frac{{\mathbf{v}}_i}{||{\mathbf{v}}_i||}$.

CCIPCA算法如下图所示：

3.2 示例程序

# CCIPCA
import numpy as np
import time
from sklearn.datasets import load_digits
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import train_test_split
X, y = load_digits(return_X_y=True)
k = 28
V = np.zeros((k, 64))
n = 1
mt = 0.1*np.random.randn(64)
tic = time.time()

for j in range(len(X)):
    u = X[j]
    if n == 1: mt = mt + u
    else: mt = float(n-1)*mt/n + u/float(n)
    u1 = u-mt   
    for i in range(min(k, n)):
        if (i+1) == n: V[i,:] = u1
        else:
            V[i,:] = (n-1)*V[i,:]/float(n)+(np.linalg.norm(u1)**2)*V[i,:]/(n*np.linalg.norm(V[i,:]))
            u1 = u1 - np.sum(u1*V[i,:].reshape(-1))*V[i,:]/(np.linalg.norm(V[i,:])**2)
    n = n+1
toc = time.time() 
W = V/np.linalg.norm(V, axis=1, keepdims=True)
X = X-mt 
X_train, X_test, y_train, y_test = train_test_split(X, y)
knn_clf = KNeighborsClassifier()
X_train_dunction = np.dot(V, X_train.T).T
X_test_dunction = np.dot(V, X_test.T).T
knn_clf.fit(X_train_dunction, y_train)
print (knn_clf.score(X_test_dunction, y_test))
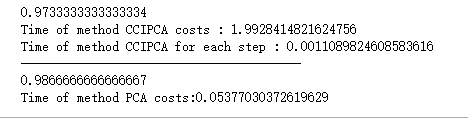
print("Time of method CCIPCA costs : "+str(toc-tic)) 
print ('----' * 10)

tic = time.time()
knn_clf = KNeighborsClassifier()
pca = PCA(n_components=0.95)
pca.fit(X_train, y_train)
X_train_dunction = pca.transform(X_train)
X_test_dunction = pca.transform(X_test)
knn_clf.fit(X_train_dunction, y_train)
print (knn_clf.score(X_test_dunction, y_test))
toc = time.time()
print ('Time of method PCA costs:'+str(toc-tic)) 

特征向量可视化：
经过CCIPCA降维后，28个特征向量如下所示。

3.3 结果分析

以上示例与结果表明，增量式PCA（CCIPCA）算法的恢复精度略低于原始的PCA算法。对于同样数量的样本，CCIPCA的总计算时间成本明显高于原始PCA。但是，PCA的时间成本约为CCIPCA的每一步更新时间成本的50倍。另一方面，CCIPCA解决的一个最重要的问题，就是使学习系统能够仅依赖依次到来的新数据，学习特征向量。CCIPCA随着数据的不断加入，降维模型也不断更新。CCIPCA还有一个好处【也是增量式学习的好处】就是：它的降维模型的训练与利用是可以并存的，这使得CCIPCA可以作为学习系统的终身学习算法。（原始PCA需要在训练结束后，才能使用学习到的降维模型。）

4. 发育网络的核心算法——CCILCA

Candid Covariance-Free Incremental Principal Component Analysis 直接协方差无关的增量式，简称CCILCA

4.1 叶成分

在给定神经元个数$c$，叶成分分析（LCA）将样本空间$\mathcal{X}$划分成$c$个不重叠的区域，我们称其为叶子区域:
$$\mathcal{X}=\mathcal{R}\cup \mathcal{R}\cup ...\cup {\mathcal{R}}_c$$
其中，如果$i\ne j$,则有${\mathcal{R}}_i\cup {\mathcal{R}}_j=\varnothing$，具体叶成分可参照下图。

每一个叶区域可以由一个单独的特征向量${\mathbf{v}}_i$表示，被称为叶成分。这些叶成分不需要正交，也不需要线性独立。它们撑起一个叶特征子空间$S$
S = s p a n { v 1 , v 2 , . . . , v c } S=span\{\mathbf{v}_1, \mathbf{v}_2, ..., \mathbf{v}_c\} S=span{v1​,v2​,...,vc​}

通常情况下，子空间$S$的维数可以比原始输入空间$\mathcal{X}$的维数要低。

4.2 算法推导

给定状态空间$\mathcal{X}$的数据集$\mathbf{X}$,我们可以通过
R j = { x ∣ j = a r g max ⁡ 1 ≤ i ≤ c x T v i } \mathcal{R}_j=\{\mathbf{x}|j=arg \max_{1 \leq i \leq c} \mathbf{x}^T \mathbf{v}_i\} Rj​={x∣j=arg1≤i≤cmax​xTvi​}
将$\mathbf{X}$划分到各叶区域${\mathcal{R}}_i,i=1,2,...,c$中，得到与各叶区域相关的子数据集${\mathbf{X}}_i,i=1,2,...,c$。

那么在已知${\mathbf{X}}_i$，我们怎么求${\mathcal{R}}_i$的最优特征向量${\mathbf{v}}_i$呢?

该问题可转变成最大化期望
$$E[||{\mathbf{x}}_{ij}^T{\mathbf{v}}_i|{|}^2]=\sum _{j=1}^{N_i}({\mathbf{x}}_{ij}^T{\mathbf{v}}_i{)}^T({\mathbf{x}}_{ij}^T{\mathbf{v}}_i)={\mathbf{v}}_i^T{\mathbf{\Sigma }}_i{\mathbf{v}}_i={\lambda }_i$$

其中，${\mathbf{\Sigma }}_i={\sum }_{j=1}^{N_i}{\mathbf{x}}_{ij}{\mathbf{x}}_{ij}^T$为子数据集${\mathbf{X}}_i$的总协方差,${\sum }_{i=1}^c{N}_i=N$为$\mathbf{X}$中元素总个数。

根据PCA的的基本理论，可知上式中取与最大特征值${\lambda }_{imax}$对应的特征相向量${\mathbf{v}}_i$为最优特征向量。

因此，针对每个叶区域，特征向量的核心迭代更式与CCIPCA相同，如下图所示。

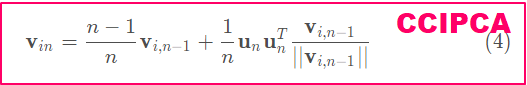
由于每个叶区域${\mathcal{R}}_i$只需要维护一个最优的${\mathbf{v}}_i$，可以看作是CCIPCA(维护$k$个特征向量)的特殊形式。【此处结论：CCILCA算法的基础元件是CCIPCA算法。】

$${\mathbf{v}}_{i{n}_i}=\frac{n_i-1}{n_i}{\mathbf{v}}_{i,n_i-1}+\frac{1}{n_i}{y}_{i{n}_i}{\mathbf{x}}_n$$

其中，$y_{i{n}_i}=\frac{{\mathbf{x}}_n^T{\mathbf{v}}_{i,n_i-1}}{||{\mathbf{v}}_{i,n_i-1}||}$为第$n$个输入${\mathbf{x}}_n$对第$i$个叶区域的响应值，该值度量当前状态与该叶区域的相似性，相似性越高表明${\mathbf{x}}_n$属于${\mathcal{R}}_i$的可能性越大。

其于以上分析可总结CCILCA的算法如下：
CCILCA算法

4.3 例子程序

# CCILCA
import numpy as np
from sklearn.datasets import load_digits
 
X, _ = load_digits(return_X_y=True)

c = 10  #feature nodes numbers
k = 1  # topk

V = np.zeros((c, 64))
n = np.ones(c)
for i in range(c):
    index = np.random.randint(len(X))
    V[i] = X[index]

def topk(array, k):
    k_index = np.argpartition(-array, k-1)[0:k+1]
    k_array = array[k_index]
    ynorm = [(k_array[i]-k_array[-1])/(k_array[0]-k_array[-1]) for i in range(k)]
    return k_array, k_index, ynorm

for j in range(1, len(X)):
    index = np.random.randint(len(X))
    xt = X[index]
    Vnorm = np.linalg.norm(V, axis=1)
    Y = np.array([np.sum(xt*V[a])/Vnorm[a] for a in range(c)])
    k_array, k_index, ynorm = topk(Y, k)
    for i in range(k):
        n[k_index[i]] += ynorm[i]
        V[k_index[i],:] = (n[k_index[i]]-1)*V[k_index[i],:]/float(n[k_index[i]])+k_array[i]*xt/float(n[k_index[i]])

特征向量可视化：
经过CCILCA学习后，10个特征向量如下所示（题图标号只是特征向量的序号而已，并不是类标）。

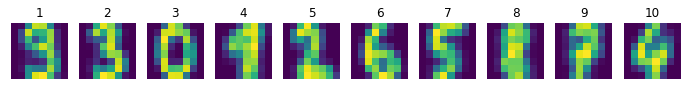
将学习到的特征向量应用于分类问题

from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import train_test_split
knn_clf = KNeighborsClassifier()
emdX = np.dot(X, V.T) # 利用特征向量组成的转换矩阵将数据转换到特征空间
X_train, X_test, y_train, y_test = train_test_split(emdX, y)    

knn_clf.fit(X_train, y_train)
print (knn_clf.score(X_test, y_test))

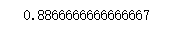
4.4 结果分析

以上示例与结果表明，增量式叶成分分析（CCILCA）算法可以学习得到一个聚类模型，每个聚类中心可用相应的特征向量表示。CCILCA也可以作为降维算法使用，上面我们利用学习到的特征向量将数据转换到特征空间后，再学习分类任务。在测试数据集上的准确率为88.6%，不是很高（毕竟从64维降到了10维）。
另外，CCILCA作为发育网络的核心算法是用于整个网络中的节点更新的全局算法，而CCIPCA则是单个节点的更新算法。这一节主要是介绍了发育网络的核心算法CCILCA，本节可以作为【博客】发育网络(DN): 一个涌现的图灵机的补充内容。

总结

主成分分析作为最经典的特征学习算法之一，已经被广泛应用于机器学习的数据预处理中。但是，主成分分析仅利用了输入状态空间的信息对特征进行学习，它只能保证利用剩余的k维特征还原原始状态数据的准确率。 由于PCA完全忽略标签、有监督信号的信息，因此：PCA并没有把握一定能提高后续机器学习任务的效果，也没有把握能够防止过拟合问题。

实际数据中，各维度可能具有物理意义，也可能没有物理意义，这些维度上的数据尺度有可能相差非常大，加上每个维度对最终的学习结论（分类结果、回归值）的重要性也不是相等的。有些维度的数值比其他维度的数值小太多，但是该维度可能与结论有很大的关联。这种数值幅值比其他维度数值小太多的维度往往会被PCA当作噪声舍弃。因此，PCA可能一不小心就帮我们败掉了数据90%的信息。

对于聚类任务，或者只有状态数据，而无标签信息可用的任务时，预处理（只能）上各种PCA就行了。对于分类或回归任务，如果输入状态空间的各维度是经过专业设计考量的，那么（懒的话）PCA也能用。不过，我们放弃的那些信息，肯定会影响最终的学习效果。

对于输入状态空间各维度的设计不是那么讲究（又或者说，很难通过主观经验设计好）的分类与回归任务，我们怎么办呢？我们怎么将标签信息加入到特征学习中？特征学习可以学出状态各维度的重要性吗？答案是肯定的。后续我将继续总结特征学习相关的研究。

参考文献

[1] Weng J , Zhang Y , Hwang W S . Candid covariance-free incremental principal component analysis[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2003, 25(8):0-1040.
[2] Weng J , Luciw M . Dually Optimal Neuronal Layers: Lobe Component Analysis[J]. IEEE Transactions on Autonomous Mental Development, 2009, 1(1):68-85.