【凸优化学习笔记3】几种重要的凸集
参考资料:
1.凌青老师的凸优化课(b站)
2.Stephen Boyd的《凸优化》中译本(清华大学出版社)
全部使用LaTex公式书写
仿射集、凸集、凸锥总结
上一篇文章讲到9个概念:
仿射集、凸集、凸锥(集)
仿射组合、凸组合、凸锥组合
仿射包、凸包、凸锥包
要从组合的概念切入去理解。
因为集是从组合定义的,包是从组合构造的。
设一个集合
C
C
C中取任意
k
k
k个点
x
1
,
.
.
.
,
x
k
x_1,...,x_k
x1,...,xk,且选取
θ
1
,
.
.
.
,
θ
k
∈
R
{\theta}_1,...,{\theta}_k\in\mathbf{R}
θ1,...,θk∈R,
我们构造新点:
θ
1
x
1
+
⋯
+
θ
k
x
k
\theta_{1} x_{1}+\cdots+\theta_{k} x_{k}
θ1x1+⋯+θkxk
对于这个新点,根据系数条件不同有:
| 新点的组合类型 | 条件 |
|---|---|
| 仿射组合 | θ 1 + . . . + θ k = 1 {\theta}_1+...+{\theta}_k=1 θ1+...+θk=1 |
| 凸组合 | θ 1 + . . . + θ k = 1 {\theta}_1+...+{\theta}_k=1 θ1+...+θk=1, θ 1 + . . . + θ k ⩾ 0 {\theta}_1+...+{\theta}_k\geqslant0 θ1+...+θk⩾0 |
| 凸锥组合 | θ 1 + . . . + θ k ⩾ 0 {\theta}_1+...+{\theta}_k\geqslant0 θ1+...+θk⩾0 |
有了组合的概念,就能定义集。比如一个集合中任意点的仿射组合还在这个集合中,这个集合就是一个仿射集。
有了组合的概念,我们还能定义包。比如一个集合中任意点的凸组合,可构造出这个集合的凸包。
几种重要的凸集
空集、单点集、n维空间和子空间、直线和线段、射线
①空集
空集是仿射集、凸集、凸锥。
②单点集
一个点的集合(单点集)是仿射集、凸集,但不是凸锥。除非这个点是原点。
③
R
n
\mathbf{R}^{n}
Rn空间和子空间
一个
R
n
\mathbf{R}^{n}
Rn空间是仿射集、凸集、凸锥。
对于一个
R
n
\mathbf{R}^{n}
Rn空间的子空间,它满足加法和数乘封闭。也就是过原点。
所以一个
R
n
\mathbf{R}^{n}
Rn空间的子空间是仿射集、凸集、凸锥。
④直线和线段
直线是仿射集。
如果直线过原点,它才是凸集、凸锥。
(直线如果过原点,那么它是一个高维空间的低维子空间,它一定是个凸锥)
线段一定是凸集,但不是仿射集、凸锥。
只有当线段退化成一个点,才会变成一个仿射集;当这个点是原点,才会变成一个凸锥。
⑤射线
即
{
x
0
+
θ
v
∣
θ
⩾
0
}
,
v
≠
0
\left\{x_{0}+\theta v \mid \theta \geqslant 0\right\}, v \neq 0
{x0+θv∣θ⩾0},v=0
它是凸集,但不是仿射集。
且只有当
x
0
x_{0}
x0是原点才是凸锥。
超平面与半空间
超平面(hyperplane)
即与给定向量
a
a
a内积为常数的点的集合:
{
x
∣
a
T
x
=
b
}
,
a
∈
R
n
,
a
≠
0
且
b
∈
R
\left\{x \mid a^{T} x=b\right\},a \in \mathbf{R}^{n}, a \neq 0 且 b \in \mathbf{R}
{x∣aTx=b},a∈Rn,a=0且b∈R
以二维空间为例:
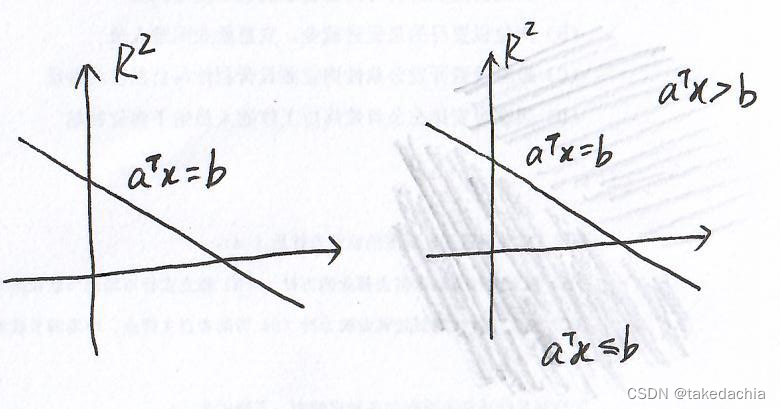
图左有一个超平面
a
T
x
=
b
a^{T} x=b
aTx=b,是一条直线。
这条直线(超平面)将这个二维空间分成了两部分:
{
x
∣
a
T
x
⩾
b
}
\left\{x \mid a^{T} x\geqslant b\right\}
{x∣aTx⩾b}、
{
x
∣
a
T
x
<
b
}
\left\{x \mid a^{T} x< b\right\}
{x∣aTx<b}
每个部分就是一个半空间(half space)。
一个超平面是一个仿射集、凸集,但不是一个凸锥。
如果这个超平面过原点,它才是一个凸锥(变成子空间了)。
半空间是一个凸集,但不是仿射集,也不是凸锥。
球和椭球
这里的球和椭球是定义在欧几里得空间中的。
球的定义:
B
(
x
c
,
r
)
=
{
x
∣
∥
x
−
x
c
∥
2
⩽
r
}
=
{
x
∣
(
x
−
x
c
)
T
(
x
−
x
c
)
⩽
r
2
}
B\left(x_{c}, r\right)=\left\{x \mid\left\|x-x_{c}\right\|_{2} \leqslant r\right\}=\left\{x \mid\left(x-x_{c}\right)^{T}\left(x-x_{c}\right) \leqslant r^{2}\right\}
B(xc,r)={x∣∥x−xc∥2⩽r}={x∣(x−xc)T(x−xc)⩽r2}
其中
x
c
x_{c}
xc是球心,
r
r
r是半径。即到球心距离小于半径的所有点集,这个距离是用二范数定义的。
球是一个凸集。
可用凸集的定义来证明,证明集合中任意两点的凸组合在集合内。
证明(证明过程中使用了三角不等式的性质):
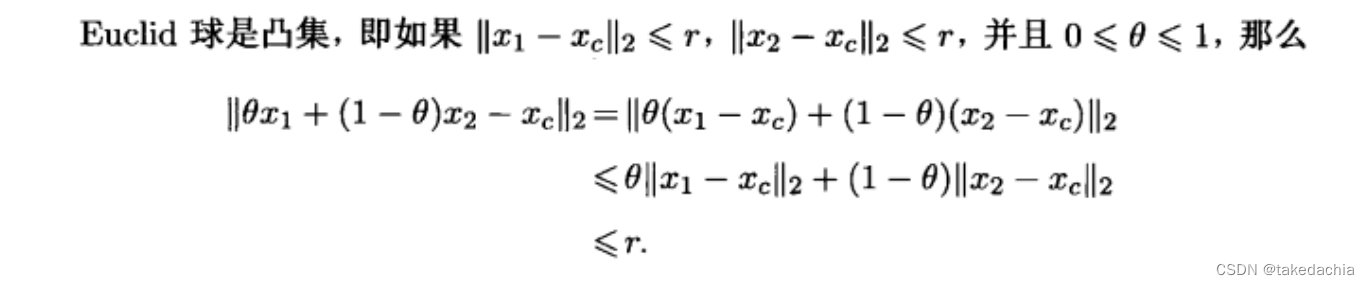
椭球的定义:
E
=
{
x
∣
(
x
−
x
c
)
T
P
−
1
(
x
−
x
c
)
⩽
1
}
\mathcal{E}=\left\{x \mid\left(x-x_{c}\right)^{T} P^{-1}\left(x-x_{c}\right) \leqslant 1\right\}
E={x∣(x−xc)TP−1(x−xc)⩽1}
这是椭球的一个加权二范数形式的表达,中间有一个矩阵P。
x
c
x_{c}
xc是椭球的中心。
P是一个对称正定矩阵,即
P
=
P
T
≻
0
P=P^{T} \succ 0
P=PT≻0。
(注:正定矩阵:奇异值都为正的矩阵。奇异值:
e
i
g
(
A
T
A
)
\sqrt{eig(A^TA)}
eig(ATA) )
P决定了椭球从
x
c
x_{c}
xc向各个方向扩展的幅度。
假设二维空间的情况下,P的两个奇异值即为椭球的半轴长。
举个简单的例子,P为对角二阶方阵(可直接得出奇异值):
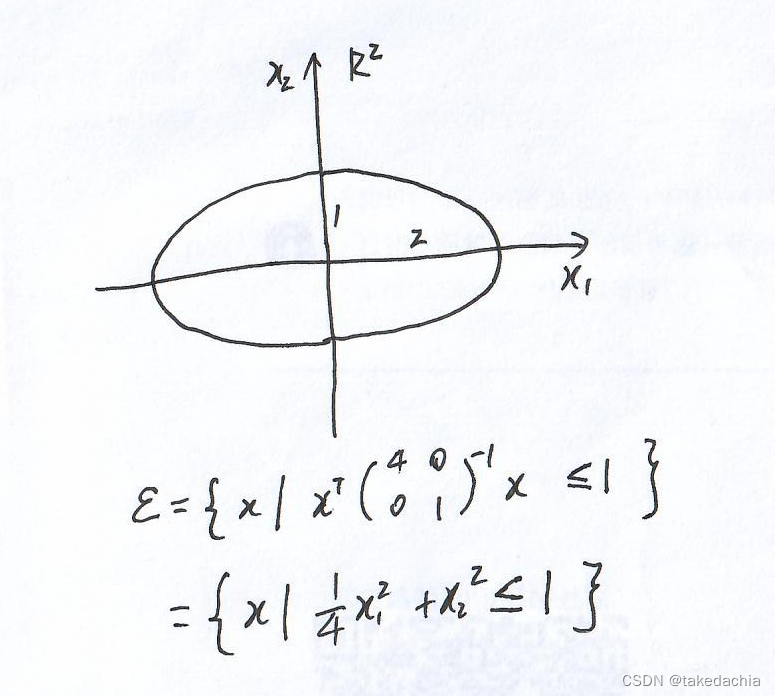
此外,如果设 P = r 2 I n P=r^2I_n P=r2In( I n I_n In为n阶单位矩阵),椭球就退化成一个球。
椭球也是一个凸集。
多面体(polyhedron)
多面体常用于线性规划。
多面体被定义为有限个线性等式和不等式的解集。
P
=
{
x
∣
a
j
T
x
⩽
b
j
,
j
=
1
,
⋯
,
m
,
c
j
T
x
=
d
j
,
j
=
1
,
⋯
,
p
}
\mathcal{P}=\left\{x \mid a_{j}^{T} x \leqslant b_{j}, j=1, \cdots, m, c_{j}^{T} x=d_{j}, j=1, \cdots, p\right\}
P={x∣ajTx⩽bj,j=1,⋯,m,cjTx=dj,j=1,⋯,p}
看上面的式子,可理解为多个半空间和超平面的交集。
比如下图是由5个半空间的交集构成的多面体:
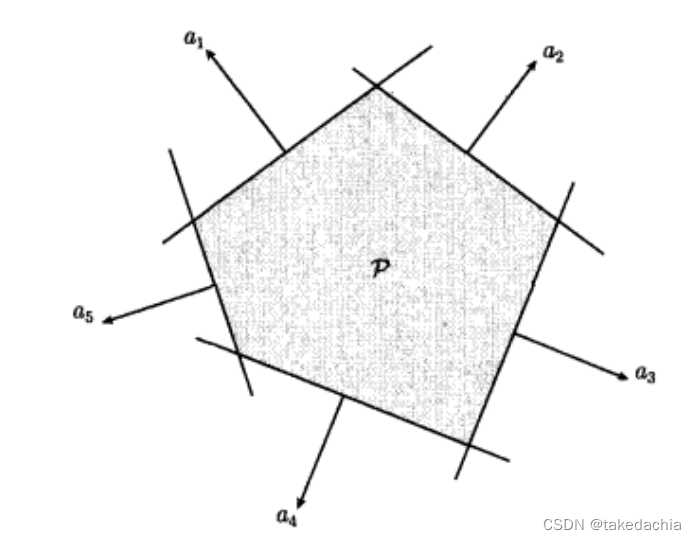
多面体是凸集。
单纯形(Simplex)
在
R
n
\mathbf{R}^{n}
Rn空间中选择
v
0
,
.
.
.
,
v
k
v_0,...,v_k
v0,...,vk 共
k
+
1
k+1
k+1 个点,
若
v
1
−
v
0
,
.
.
.
,
v
k
−
v
0
v_1-v_0,...,v_k-v_0
v1−v0,...,vk−v0 线性无关,
则与上述点相关的单纯形为:
C
=
conv
{
v
0
,
⋯
,
v
k
}
=
{
θ
0
v
0
+
⋯
+
θ
k
v
k
∣
θ
⪰
0
,
1
T
θ
=
1
}
C=\operatorname{conv}\left\{v_{0}, \cdots, v_{k}\right\}=\left\{\theta_{0} v_{0}+\cdots+\theta_{k} v_{k} \mid \theta \succeq 0, \mathbf{1}^{T} \theta=1\right\}
C=conv{v0,⋯,vk}={θ0v0+⋯+θkvk∣θ⪰0,1Tθ=1}
(式中
θ
\theta
θ 代表了所有
θ
\theta
θ组成的向量,用于表示都是非负的;
1
\mathbf{1}
1代表了k个1组成的向量,用于表示加和为1)
可见单纯形是一个基于空间中选取点集构造的凸包。
可以推出,k一般≤n维数。单纯型也称为
R
n
\mathbf{R}^{n}
Rn空间的k维单纯形。
1维单纯形是一条线段;2维单纯型是一个三角形(包含内部);3维单纯形是一个四面体。
举个2维空间中的2维单纯形例子:
(右图,k不能取到3,因为2维空间中三个向量必定线性相关)

重要结论:
单纯形是多面体的一种。即单纯形可用多面体的形式表达。
这个结论在直观上比较容易想象,比如2维空间的三角形,3维空间的四面体。
下面证明一下。
证明:Simplex是Polyhedron的一种。即Simplex可以用Polyhedron的形式表达出来。
对于 C = conv { v 0 , ⋯ , v k } = { θ 0 v 0 + ⋯ + θ k v k ∣ θ ⪰ 0 , 1 T θ = 1 } C=\operatorname{conv}\left\{v_{0}, \cdots, v_{k}\right\}=\left\{\theta_{0} v_{0}+\cdots+\theta_{k} v_{k} \mid \theta \succeq 0, \mathbf{1}^{T} \theta=1\right\} C=conv{v0,⋯,vk}={θ0v0+⋯+θkvk∣θ⪰0,1Tθ=1},
我们知道 C C C是 R n \mathbf{R}^{n} Rn空间中的k维单纯形。
即证:对于任意 x ∈ C x\in C x∈C,都可以用一组线性不等式和等式来表示。
↓
根据单纯形定义, x ∈ C x\in C x∈C可知: x = θ 0 v 0 + θ 1 v 1 + ⋯ + θ k v k x=\theta_{0} v_{0}+\theta_{1} v_{1}+\cdots+\theta_{k} v_{k} x=θ0v0+θ1v1+⋯+θkvk, θ ⪰ 0 , 1 T θ = 1 \theta \succeq 0, \mathbf{1}^{T} \theta=1 θ⪰0,1Tθ=1
∵ 1 T θ = 1 \mathbf{1}^{T} \theta=1 1Tθ=1
∴ x x x右边构造成:
x = ( 1 − θ 1 − . . . − θ k ) v 0 + θ 1 v 1 + ⋯ + θ k v k x=(1-\theta_{1}-...-\theta_{k}) v_{0}+\theta_{1} v_{1}+\cdots+\theta_{k} v_{k} x=(1−θ1−...−θk)v0+θ1v1+⋯+θkvk
= v 0 + θ 1 ( v 1 − v 0 ) + . . . + θ k ( v k − v 0 ) =v_{0}+\theta_{1}(v_{1}-v_{0})+...+\theta_{k}(v_{k}-v_{0}) =v0+θ1(v1−v0)+...+θk(vk−v0)
我们定义 y = ( θ 1 , ⋯ , θ k ) y=\left(\theta_{1}, \cdots, \theta_{k}\right) y=(θ1,⋯,θk), B = [ v 1 − v 0 ⋯ v k − v 0 ] ∈ R n × k B=\left[\begin{array}{lll}v_{1}-v_{0} & \cdots & v_{k}-v_{0}\end{array}\right] \in \mathbf{R}^{n \times k} B=[v1−v0⋯vk−v0]∈Rn×k
∴ 可得式子: x = v 0 + B y x=v_{0}+B y x=v0+By
∵ v 1 − v 0 , . . . , v k − v 0 v_1-v_0,...,v_k-v_0 v1−v0,...,vk−v0 线性无关
∴ r a n k ( B ) = k rank(B)=k rank(B)=k(即矩阵B的秩为k,为一个n行k列的列满秩矩阵)
对于一个列满秩矩阵,我们可以通过初等行变换,变换成这样一个矩阵:
[ I k × k 0 ( n − k ) × k ] \left[\begin{array}{l}I^{k \times k} \\ 0^{(n-k) \times k}\end{array}\right] [Ik×k0(n−k)×k]
∴ 一定存在这样一个变换矩阵,我们设变换矩阵为 A n × n A^{n \times n} An×n(一个可逆的方阵),A可以分成上下两个分块 A 1 , A 2 A_1,A_2 A1,A2,即:
A B = [ A 1 k × n A 2 ( n − k ) × n ] B = [ I 0 ] A B=\left[\begin{array}{l}A_{1}^{k \times n} \\ A_{2}^{(n-k) \times n}\end{array}\right] B=\left[\begin{array}{l}I \\ 0\end{array}\right] AB=[A1k×nA2(n−k)×n]B=[I0]
那么我们把式子 x = v 0 + B y x=v_{0}+B y x=v0+By左乘 A A A:
A x = A v 0 + A B y A x=A v_{0}+ABy Ax=Av0+ABy
把 A A A拆分为上下分块 A 1 , A 2 A_1,A_2 A1,A2后,分开来写,得到:
A 1 x = A 1 v 0 + y , A 2 x = A 2 v 0 A_{1} x=A_{1} v_{0}+y, \quad A_{2} x=A_{2} v_{0} A1x=A1v0+y,A2x=A2v0 这两个式子
∵ y y y是我们设的一个变量 ( θ 1 , ⋯ , θ k ) \left(\theta_{1}, \cdots, \theta_{k}\right) (θ1,⋯,θk),由于里面没有 θ 0 {\theta}_0 θ0
∴ 可得到 y ⪰ 0 y \succeq 0 y⪰0, 1 T y ⩽ 1 \mathbf{1}^{T} y \leqslant 1 1Ty⩽1 这两个不等式条件
因此,代入上面两个式子中第一个式子;再加上第二个式子,可得:
① A 1 x ⪰ A 1 v 0 A_{1} x \succeq A_{1} v_{0} A1x⪰A1v0
② 1 T A 1 x ⩽ 1 + 1 T A 1 v 0 \mathbf{1}^{T} A_{1} x \leqslant 1+\mathbf{1}^{T} A_{1} v_{0} 1TA1x⩽1+1TA1v0
③ A 2 x = A 2 v 0 A_{2} x=A_{2} v_{0} A2x=A2v0
这三个式子是 x x x的线性等式和不等式,故其描述了一个多面体,得证。
对称矩阵集合
来看下面三个对称 n × n {n \times n} n×n矩阵的集合:
对称矩阵集合:
S
n
=
{
X
∈
R
n
×
n
∣
X
=
X
T
}
\mathbf{S}^{n}=\left\{X \in \mathbf{R}^{n \times n} \mid X=X^{T}\right\}
Sn={X∈Rn×n∣X=XT}
对称半正定矩阵的集合:
S
+
n
=
{
X
∈
S
n
∣
X
⪰
0
}
\mathbf{S}_{+}^{n}=\left\{X \in \mathbf{S}^{n} \mid X \succeq 0\right\}
S+n={X∈Sn∣X⪰0}
(符号
⪰
\succeq
⪰ 的意思是矩阵所有特征值都大于等于0)
对称正定矩阵的集合:
S
+
+
n
=
{
X
∈
S
n
∣
X
≻
0
}
\mathbf{S}_{++}^{n}=\left\{X \in \mathbf{S}^{n} \mid X \succ 0\right\}
S++n={X∈Sn∣X≻0}
这三个矩阵是否是凸集呢?矩阵是难以进行空间想象的。
我们先研究对称半正定矩阵集合
S
+
n
\mathbf{S}_{+}^{n}
S+n。
结论:对称半正定矩阵集合
S
+
n
\mathbf{S}_{+}^{n}
S+n是一个凸锥。
证明:
取任意系数 θ 1 , θ 2 ⩾ 0 \theta_{1},\theta_{2}\geqslant0 θ1,θ2⩾0,并取任意矩阵 A , B ∈ S + n A, B \in \mathbf{S}_{+}^{n} A,B∈S+n,即证:
θ 1 A + θ 2 B ∈ S + n \theta_{1} A+\theta_{2} B \in \mathbf{S}_{+}^{n} θ1A+θ2B∈S+n
根据半正定矩阵的定义,我们有:
x T A x ⩾ 0 x^{T} A x\geqslant0 xTAx⩾0, x T B x ⩾ 0 x^{T} B x\geqslant0 xTBx⩾0
那么 x T ( θ 1 A + θ 2 B ) x = θ 1 x T A x + θ 2 x T B x ⩾ 0 x^{T}\left(\theta_{1} A+\theta_{2} B\right) x=\theta_{1} x^{T} A x+\theta_{2} x^{T} B x \geqslant 0 xT(θ1A+θ2B)x=θ1xTAx+θ2xTBx⩾0
证得 θ 1 A + θ 2 B \theta_{1} A+\theta_{2} B θ1A+θ2B 是半正定矩阵。
又因为同形对称矩阵的数乘和加和不改变对称性,
所以矩阵 θ 1 A + θ 2 B \theta_{1} A+\theta_{2} B θ1A+θ2B 是一个对称半正定矩阵,得证。
所以,
对称半正定矩阵集合
S
+
n
\mathbf{S}_{+}^{n}
S+n是一个凸锥。
对称矩阵集合
S
n
\mathbf{S}^{n}
Sn也是一个凸锥。(同形对称矩阵的数乘和加和不改变对称性)
然而,
对称正定矩阵集合
S
+
+
n
\mathbf{S}_{++}^{n}
S++n 只是一个凸集,不是凸锥。
(可回到上面的证明,由于
θ
1
,
θ
2
\theta_{1},\theta_{2}
θ1,θ2可取到0,因此根据正定矩阵定义,
θ
1
A
+
θ
2
B
\theta_{1} A+\theta_{2} B
θ1A+θ2B没办法证明大于0)
教材中举了2维空间中的半正定矩阵集合:
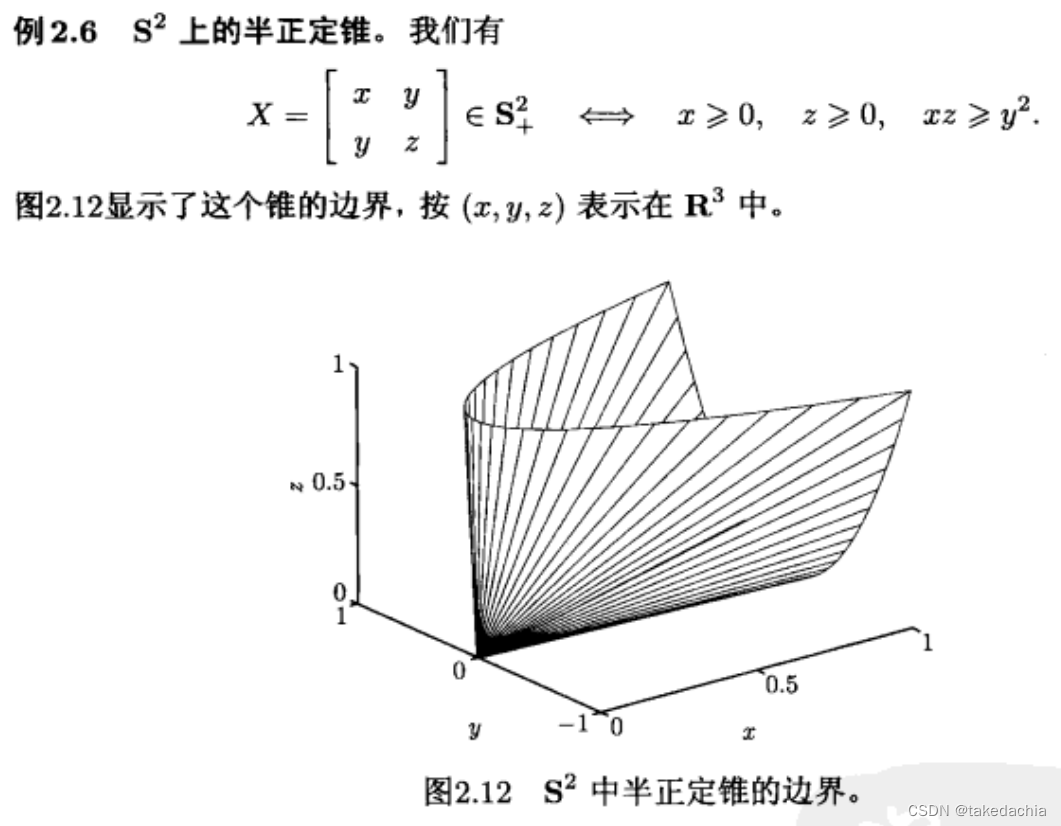
相关文章
- MicroPython内核开发笔记书内软件用例 :浮点数相关实验
- 机器学习笔记之核方法(一)核方法思想与核函数介绍
- 机器学习笔记之马尔可夫链蒙特卡洛方法(一)蒙特卡洛方法介绍
- 机器学习笔记之线性回归——从概率密度函数角度认识最小二乘法
- 机器学习笔记之指数族分布——最大熵角度观察指数族分布(二)最大熵定理与指数族分布的关系
- CSDN日报191014:计算机大数乘法引发的思考;TensorFlow2.0 笔记
- 阿里亿级并发册 + 机器学习算法 + 面试册 + 优化册 + 代码册 笔记!!!
- 数据库常用命令笔记
- [转]ListView学习笔记(一)——缓存机制
- PHP全栈学习笔记9
- 公众号开发笔记二
- BI产品学习笔记
- tensorflow学习笔记五:mnist实例--卷积神经网络(CNN)
- Dynamic CRM 2013学习笔记(七)追踪、监控及性能优化
- Java_jdbc 基础笔记之十 数据库连接 (ResultSetMetaData 类)
- Tensorflow2.0 入门与实战学习笔记(一、二)-优化函数、学习率、反向传播
- C++基础学习笔记----第十三课(操作符重载-下)
- javascript学习笔记
- 零基础学前端之SEO 基础知识学习--SEO优化学习教程【学习笔记】
- Linux学习笔记(19)linux定时任务(crontab)
- MongoDB学习笔记—Linux下搭建MongoDB环境
- nginx 学习笔记(1) nginx安装
- 学习笔记(31):Python网络编程&并发编程-定时器
- 【学习笔记】笔记本电脑快速查看WiFi密码(Win11版本)
- sql注入学习笔记,什么是sql注入,如何预防sql注入,如何寻找sql注入漏洞,如何注入sql攻击 (原)
- json学习笔记

