数据挖掘十大算法之分类算法(决策树模型)

接上篇文章分类介绍及评价指标我们讨论了分类算法中，分类模型的选择是非常关键的一步，接下来我们分析常用的分类模型——决策树模型

在本文中没有举例，全部为概念，所有举例都在ID3算法的学习中

1. 决策树的概念

决策树是一种树形结构，决策树包含一系列规则，一般我们使用决策树将大型记录集分割为小记录集，通过每一次连续分割，结果集中的成员彼此变得越来越相似。

例如我们想用决策树来分类下面表中的数据，来分析什么样的人群会购买电脑：

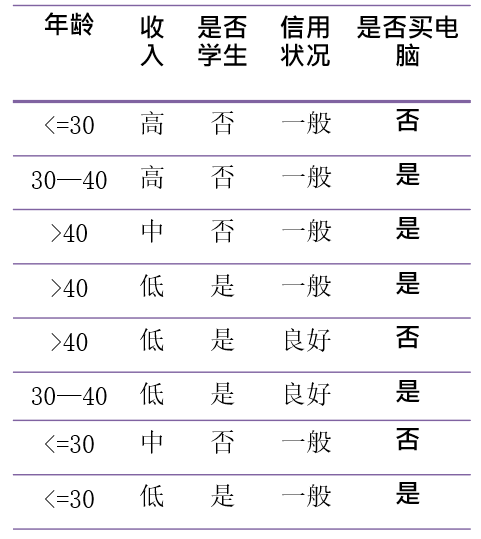
那我们可以生成下图所示的决策树，可以看到，通过决策树我们可以更加清晰的对数据集进行分类，快速找到我们想要的数据并得出结论，例如下面的决策树中，我们可以快速知道，年龄小于30岁的学生一定会买电脑、年龄大于40岁且信用良好的人一般也会购买电脑

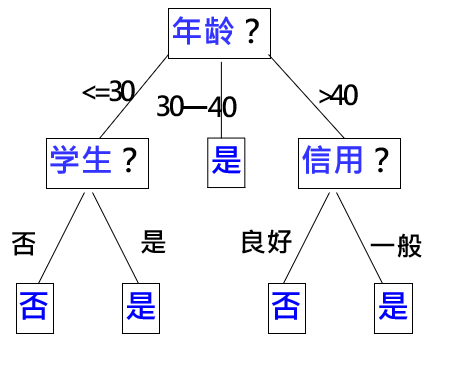
决策树里面的结点分为：

• 根节点（root node）
• 内部节点（internal node）
• 叶节点（leaf node）

在决策树中，每个叶子结点都有一个叶标号，非叶子结点（包括根结点和内部结点）包含属性测试条件，用于分开具有不同特性的记录

决策树算法的优点从上面的图也能明显感受到：

• 是一种非参数方法，不要求任何先验假设，不假定类和其他属性服从一定的概率分布。
• 决策树的训练时间相对较少，即使训练集很大，也可以快速地构建分类模型。
• 决策树的分类模型是树状结构，简单直观，符合人类的理解方式。
• 可以将决策树中到达每个叶节点的路径转换为IF—THEN 形式的分类规则，这种形式更有利于理解。
• 对于噪声的干扰具有较好的鲁棒性。

决策树算法的缺点：

• 决策树的缺点在于决策树属于贪心算法，只能局部最优，其次对于何时停止剪枝需要有较难的把握
• 决策树的应用是通过未分类实例的属性与决策树比较，实现对未分类实例的类别判定

2. 构建决策树

决策树通常有两个步骤：决策树构造（Tree Building）、决策树剪枝（Tree Pruning）

• 决策树构建：树构造阶段决策树采用自顶向下的递归方式从根节点开始在每个节点上按照给定标准选择测试属性，然后按照相应属性的所有可能取值向下建立分枝、划分训练样本，直到一个节点上的所有样本都被划分到同一个类，或者某一节点中的样本数量低于给定值时为止。
• 树剪枝阶段：构造过程得到的并不是最简单、紧凑的决策树，因为许多分枝反映的可能是训练数据中的噪声或孤立点。树剪枝过程主要检测和去掉这种分枝，以提高对未知数据集进行分类时的准确性

当然这里只是介绍了一下决策树构建的步骤，如果没有案例的话可能会比较难以理解，在下一篇文章中会通过对ID3算法来进行决策树构建

3. 决策树中的信息论原理

决策树是利用信息论原理对大量样本的属性进行分析和归纳而产生的，这里主要介绍决策树中用到的信息论基础知识

我们需要针对一下几个概念进行学习，这些概念将贯穿所有基于决策树的算法，例如ID3、C4.5算法：

• 信息量
• 熵
• 分类集合信息量
• 信息增益度

首先我们要知道在信息论（大学里学的概率论也有）中的一些基础知识：

• 样本空间：随机试验的所有可能结果组成的集合称为样本空间。对于抛掷硬币试验，样本空间 = { 正面，反面} 。

• 样本点：样本空间中的元素称为样本点， “正面”就是上述样本空间的一个样本点。

• 随机事件：样本空间的子集。在每次试验中，当且仅当该子集中的任意一个元素发生时，称该随机事件发生。

• 随机变量：是定义在样本空间上的映射。通常是将样本空间映射到数字空间，这样做的目的是方便引入高等数学的方法来研究随机现象。需要指出的是，对于随机事件A，P（A）表示随机事件发生的概率；对于随机变量X，我们一般这么写，P（X = x）表示随机变量取值为x的概率。其中x是一个确定的值。

  举个栗子：

  例如在掷一次骰子的随机试验中，设随机事件A = 偶数点朝上。那么当我们在掷出{2,4,6}这个集合中的任意一个点的时候，我们都可以说：随机事件A发生了。集合{2,4,6}就是样本空间

  如果将正面与1对应，反面与0对应，那么样本空间= { 正面，反面 } 与 随机变量X = { 1，0 } 之间建立起了一一对应的关系

3.1 信息量

信息论的提出者克劳德·艾尔伍德·香农是最早开始信息论研究的科学家之一，在他的研究下我们才有了以下信息论概念：

信息量: 是概率空间中的单一事件或离散随机变量的值相关的信息的量度

比如吃瓜群众经常说某某明星的某条微博信息量很大，这里“信息量” 指的就是这个定义

那么到底如何计算信息量呢？由定义，当信息被拥有它的实体传递给接收它的实体时，仅当接收实体不知道信息的先验知识时信息才得到传递。如果接收实体事先知道了消息的内容，这条消息所传递的信息量就是0。只有当接收实体对消息对先验知识少于100%时，消息才真正传递信息。

因此，一个随机产生的事件𝜔𝑛所包含的自信息数量，只与事件发生的几率相关。事件发生的几率越低，在事件真的发生时，接收到的信息中，包含的自信息越大。

既然信息量和随机事件发生的概率有关，不妨将𝜔𝑛的信息量写作
$$
𝐼 (𝜔𝑛)= 𝑓[𝑝( 𝜔𝑛) ]

$$
由之前的分析，如果𝑝( 𝜔𝑛) = 1， 𝐼( 𝜔𝑛)= 0，且当𝑝( 𝜔𝑛) <1， 𝐼( 𝜔𝑛)>0

此外，根据定义，自信息的量度是非负的而且是可加的。如果事件C是两个独立事件A和B的交 集，那么宣告C发生的信息量就等于分别宣告A和事件 B的信息量的和：
$$I(C)=I(A\cap B)=I(A)+I(B)$$
因为A和B是独立事件，所以
$$
𝑃(𝐶) = 𝑃 ( 𝐴 ∩ 𝐵)= 𝑃(𝐴)⋅ 𝑃( 𝐵)

Font metrics not found for font: .
I(\omega_n) = -log[P(\omega_n)] = log(\frac{1}{P(\omega_n)})
$$
上面这个公式非常重要，可以先将其记住，后面再实践中再慢慢进行理解

在上面的定义中，没有指定的对数的基底：如果以2为底，单位是bit。当使用以 e 为底的对数时，单位将是 nat。对于基底为 10 的对数，单位是 hart。决策树算法使用以2为底，后续不再提及。显然的，该式符合人们的直观概念，某事件发生的概率越小，那么当该事件发生时所带来的信息量就越大。

3.2 熵

我们在高中的课程里面学习过，熵是用来衡量混乱程度的物理量。例如一盒整齐的火柴掉在地上被打乱了，这就是一个熵增的过程

这里我们给出信息论中熵的概念：

设S是S 个数据样本的集合。假定类标号属性具有m 个不同 值，定义m 个不同类Ci (i = 1,…,m)。设Si 是类Ci 中的样本数。 对一个给定的样本分类所需的期望信息由下式给出：
$$I(S_1,S_2,...,S_m)=-\sum _{i=1}^m{P}_{i}lo{g}_2(P_i)$$
其中，Pi 是任意样本属于Ci 的概率，并用 si / s 估计。注意，对数函数以2为底，因为信息用二进位编码。

熵可以描述随机变量的不确定程度

信息量取决于概率，随机事件发生的概率越小，那么当该事件发生时，所蕴含的信息量越大。同时，随机事件发生的概率小⟺这件事不易控制，不易预测，即这件事的不确定度高，熵越大。

当然这里还有划分子集的熵和条件熵的概念

划分子集的熵：

设属性A 具有v 个不同值{a1 ,…, av}。可以用属性A 将S 划 分为v 个子集{S1 ,…, Sv}；其中，Sj 包含S 中这样一些样本，它们在A 上具有值aj。

设sij 是子集Sj 中类Ci 的样本数。根据A划分子集的熵或期望信息由下式给出：
$$E(A)=\sum _{j=1}^v\frac{S_{1j}+...+S_{mj}}{S}I(S_{1j,...,S_{mj}})$$
条件熵:

条件熵：条件熵描述了在已知第二个随机变量X 的值的前提下，随机变量 Y 的信息熵还有多少。基于随机变量X条件下的Y的熵，表示为H(Y|X)。

如果用H(Y|X) = x 表示为变量Y在变量X取特定值x条件下的熵，那么H(Y|X) 就是X在取遍所有的x后取平均的结果。即
H ( Y ∣ X ) = ∑ x ∈ X [ P ( x ) ∗ H ( Y ∣ X = x ) ] = ∑ x ∈ X { P ( x ) ∗ ∑ i n [ P ( y ∣ x ) ∗ l o g ( 1 P ( y ∣ x ) ) ] } H(Y|X) = \sum_{x \in X}[P(x)*H(Y|X =x)] = \sum_{x \in X}\{P(x)*\sum_i^n[P(y|x)*log(\frac{1}{P(y|x)})] \} H(Y∣X)=x∈X∑​[P(x)∗H(Y∣X=x)]=x∈X∑​{P(x)∗i∑n​[P(y∣x)∗log(P(y∣x)1​)]}
条件熵可以描述在某个随机变量确定的情况下，另一个随机变量的不确定程度。

3.3 分类集合信息量

若一个记录集合T根据类别属性的值被分为互相独立的类C1，C2，…，Ck，则识别T的一个元素属于哪个类所需要的信息量Info(T) = I(P)，其中P为C1，C2，…，Ck的概率分布，即
$$P=(\frac{|C_1|}{T},\frac{C_2}{T},\frac{C_k}{T})$$

3.4 信息增益

信息增益是两个信息量之间的差异，其中之一是确定T中元素类别的信息量，另一个信息量是在已得到的属性X的值后需确定的T中元素类别的信息量
$$Gain(X,T)=Info(T)-Info(X,T)$$
在决策树构造的过程中，最重要的步骤就是决策树节点属性的选择，我们只需要一步步的，依次找出哪个属性确定后，我们的研究目标的熵会相对下降的最多，即该属性对目标属性的信息增益最大，我们就先把这个属性确定下来，这样我们的目标就会逐渐清晰了，这就是ID3算法的核心

本文中概念比较多，并且没有相应的例子，所有关于本文概念的例子都在ID3算法的学习中