python之PCA主成分分析实现对人脸数据降维

一：总结：

（1）PCA用途：PCA是一种非常实用的数据压缩方法，在使用线性回归和神经网络算法之前都可以先使用PCA对特征进行降维

（2）PCA代码实现还原维度的方法：降维后的矩阵*他的转置+还原去均值化（进行数据还原时因为之前左过数字归一化操作，因此还需要加回去）

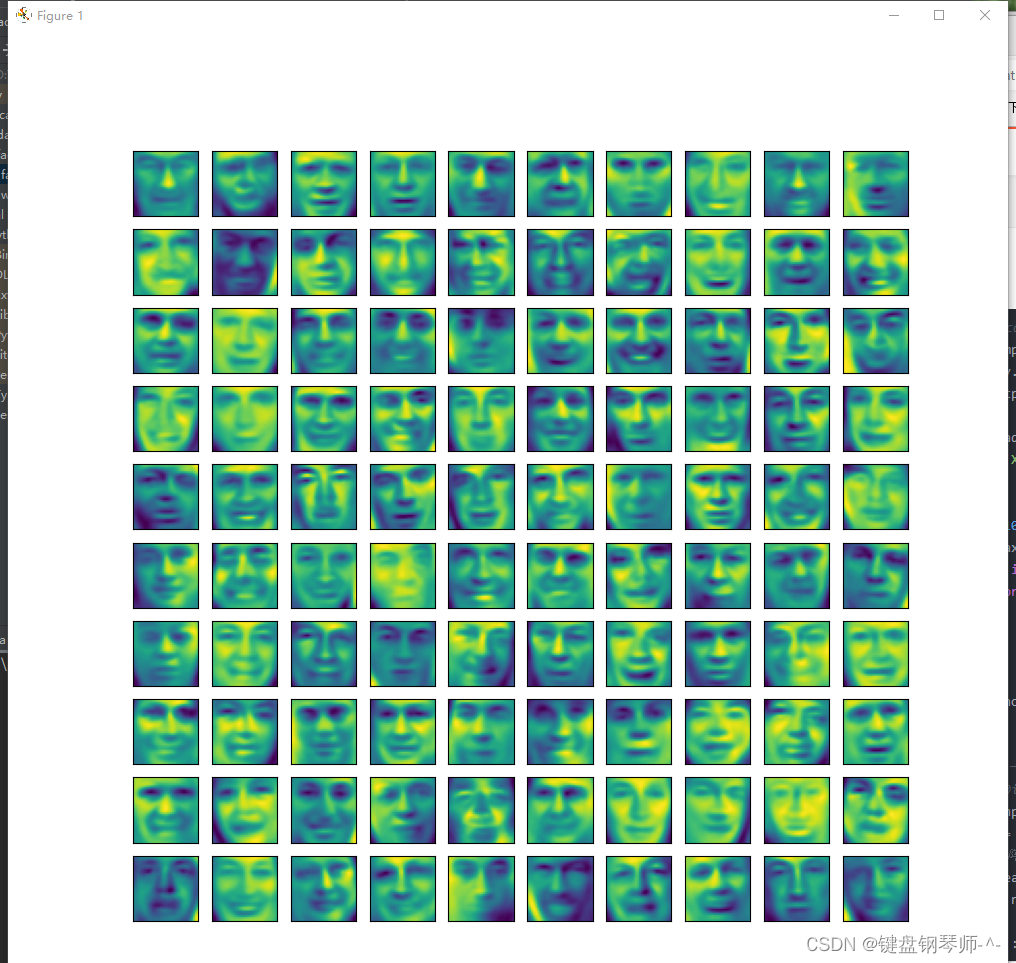
（3）原始图像为5000*1024维，对降维到36维后显示前100张图片，每张图大小为32*32；

（4将图像降到n维实际就是保留n个主要特征，其余未保留的信息对图像的呈现有一定影响但是人脸的主要信息没有丢失，丢失的是图像中一些很细节的东西，因此会有图像变模糊的感觉。

-----------------------------------------------算法开始------------------------------------------------------

算法步骤：（引用）

PCA算法代码实现

#------------导入数据-----------

import numpy as np
from scipy.io import loadmat
import matplotlib.pyplot as plt

data = loadmat('ex7data1.mat')
X = data['X']


#mean表示求平均，axis=0，那么输出矩阵是1行，求每一列的平均（按照每一行去求平均；axis=1，输出矩阵#是1列，求每一行的平均（按照每一列去求平均）

#------------ ------------去均值化-----------------
X_demean = X - np.mean(X, axis=0)


# -------------协方差矩阵----------
C = X_demean.T@X_demean / len(X_demean)

# U为特征向量， 这里U和V相等
#对协方差矩阵做SVD
U, S, V = np.linalg.svd(C)#求逆矩阵

#因为前面得到的Σ是n × n 的，行数为n，所以U是n 阶方阵，其列空间由左奇异向量组成，选取前k个列向量，组成主成分特征矩阵

U1 = U[:, 0]


#--------------------------- 实现降维---------------
#降维得到的矩阵X_reduction即为去均值化后的矩阵与
X_reduction = X_demean@U1

# --------------------------矩阵还原---------------
X_restore = X_reduction.reshape(50, 1)@U1.reshape(1,2) + np.mean(X,axis=0)

#进行数据还原时因为之前左过数字归一化操作，因此还需要加回去
#降维后的矩阵*他的转置+还原去均值化
plt.scatter(X[:, 0], X[:, 1])
plt.scatter(X_restore[:, 0], X_restore[:, 1])
plt.show()

# PCA的效果评估，可以直接通过S特征值矩阵
# print(S[0] / (S[0] + S[1]))

---------------------------------------------文件pca faces 解析--------------------------------

(1)fig, axis = plt.subplots(ncols=10, nrows=10, figsize=(10, 10))中：

figsize=(10, 10)指定绘图时图片大小，figsize 参数小了会导致图窗抖动；

（2）imshow()函数用于将数据显示为图像

（3）a.reshape(m,n)表示将原有数组a转化为一个m行n列的新数组，a自身不变。m与n的乘积等于数组中的元素总数；

（4）#axis[c, r].imshow(X[10*c + r].reshape(16,64).T)  将每个小图形化为16*64（乘积必须等于1024）：

#文件名：pca faces.py
import numpy as np
from scipy.io import loadmat
import matplotlib.pyplot as plt

data = loadmat('ex7faces.mat')
X = data['X']

#调用numpy库得到
def plot_100images(X):
    fig, axis = plt.subplots(ncols=10, nrows=10, figsize=(10, 10))#前100张图片
    for c in range(10):
        for r in range(10):
            # 这里注意要转置
            axis[c, r].imshow(X[10*c + r].reshape(32, 32).T)#每张小图32*32
            axis[c, r].set_xticks([])
            axis[c, r].set_yticks([])
    plt.show()


# 画出来瞅一眼
# plot_100images(X)
#------------------去均值化--------------------
X_mean = np.mean(X, axis=0)
X_demean = X - X_mean

# --------计算协方差矩阵-------------
C = X_demean.T @ X_demean / len(X_demean)


#--------------计算特征向量-----------------------
U, S, V = np.linalg.svd(C) #S为特征值，U为特征向量

U1 = U[:, :36]  #降到36维，那么取特征向量的前36列

X_reduction = X_demean@U1

printf("降维后的数据形状"，X_reduction.shape)
#----------------数据还原--------------------------------
X_restore = X_reduction@U1.T + X_mean           #加上各个维度的均值

plot_100images(X_restore)

"""
sklearn pca实战
"""
import numpy as np
from scipy.io import loadmat
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA

data = loadmat('ex7data1.mat')
X = data['X']
X_mean = np.mean(X, axis=0)
X_demean = X - X_mean

# n_components可以为整数，表示需要降的维数K；可以为小数，表示对方差占比的要求
pca = PCA(n_components=0.80)
pca.fit(X_demean)
# 方差占比array
print(pca.explained_variance_ratio_)
# 特征值
print(pca.explained_variance_)
# 特征向量
print(pca.components_)
# 降维后的样本
X_reduction = pca.fit_transform(X_demean)
# print(pca.fit_transform(X))
# 降维后
X_restore = pca.inverse_transform(X_reduction) + X_mean
print(X_restore)
# 测试集的均值归一和特征向量都要用训练集的
plt.scatter(X[:, 0], X[:, 1])
plt.scatter(X_restore[:, 0], X_restore[:, 1])
plt.show()

PCA降维结果：

三：预备知识【熟悉的可直接跳过，直接看代码】

（1）基于numpy,matplotlib,scipy,sklearn四个库

（2）@有两个用法：1：表示修饰符可以在模块或者类的定义层内对函数进行修饰。出现在函数定义的前一行，不允许和函数定义在同一行。2表示矩阵乘法

（3）对于矩阵a有：a.T---------表示矩阵a的转置

例如：

a
array([[1, 2, 3],
       [4, 5, 6],
       [7, 8, 9]])
a.T
array([[1, 4, 7],
       [2, 5, 8],
       [3, 6, 9]])

（4）降维作用
（1）使得数据集更容易使用
（2）降低很多算法的计算开销
（3）去除噪声
（4）多维数据不容易画图，降低维度容易画图，使结果容易理解。

优点：降低数据的复杂性，识别出最重要的多个特征。
缺点：不一定需要，有可能损失掉有用信息，仅适用于数值数据。

（5）:U[:,n]表示在全部数组（维）中取第n个数据，直观来说，U[:,n]就是取所有集合的第n个数据,

eg： U={1,2;

               2,4;

               5,0}

U[:,0]表示[1,2,5],即每一行的第0个数据;