0：串联各章

等价条件

1. ①|A|≠0，A可逆
⇦⇨②r(A)=n，A满秩
⇦⇨③α₁,α₂,…α_n线性无关
⇦⇨④Ax=0仅有零解

2. ①|A|=0，A不可逆
⇦⇨②r(A)<n，A不满秩
⇦⇨③α₁,α₂,…α_n线性相关
⇦⇨④Ax=0有非零解

第1章 行列式

求行列式

求二阶行列式：交叉相减

求三阶行列式：行/列展开定理
①若三阶行列式是上/下三角矩阵，则行列式的值直接为主对角线乘积

---

例题1：15年13.   求n阶行列式

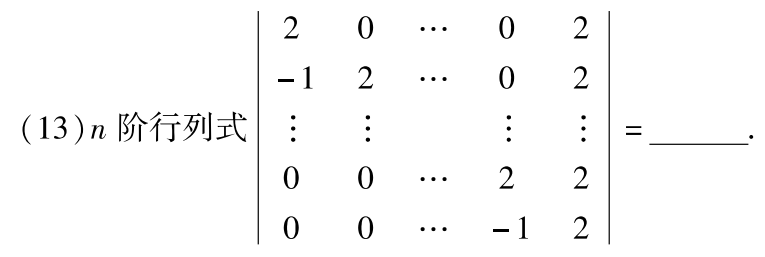
分析：

答案：$2^{n+1}-2$

---

行列式的性质

1.若A为n阶方阵，则$|kA|=k^n|A|$
2.$|A^{\ast }|=|A{|}^{n-1}$

3.分块矩阵的行列式：
(1)副对角线
若A为n阶矩阵，B为m阶矩阵，则$\left|\begin{array}{cc}O& B\\ A& C\end{array}\right|=\left|\begin{array}{cc}C& B\\ A& O\end{array}\right|=(-1{)}^{mn}|A||B|$

4.$|AB|=|A|\cdot |B|$
5.$|A|=\sum _{k=1}^n{a}_{ik}{A}_{ik}$ (i=1,2,3…n)       行列展开定理
6.不满秩、不可逆、向量组线性相关，则行列式 = 0       满秩、可逆、行列式非零、线性无关的关系

---

例题1：23李林四(一)15.

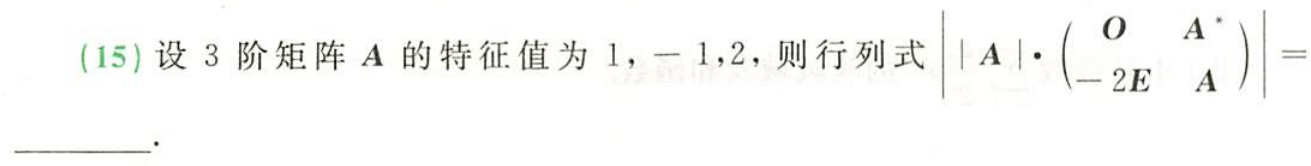
分析：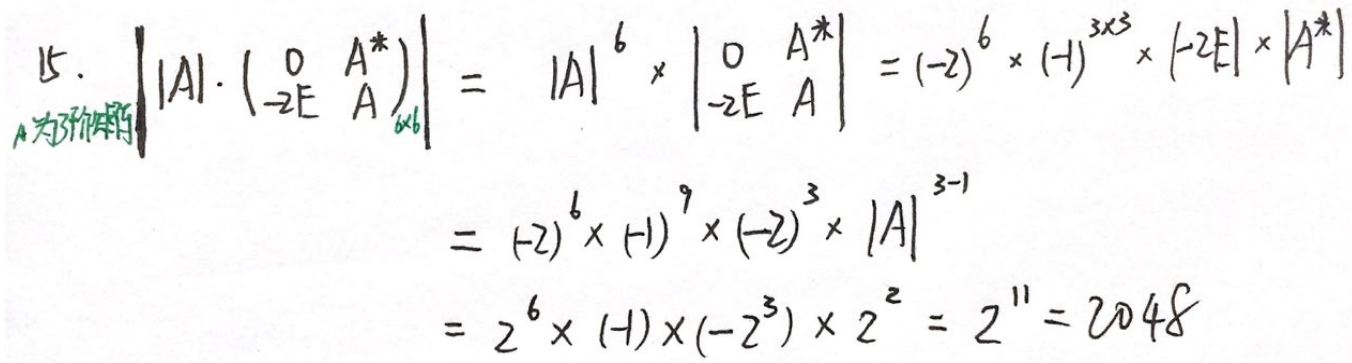
答案：2048

---

第2章 矩阵

矩阵运算

---

例题1：23李林四(一)23.

答案：

---

初等变换

以下三种变换，称为矩阵的初等变换：对行进行初等变换，称为初等行变换；对列进行初等变换，称为初等列变换
1.交换：交换矩阵任意两行或两列
2.倍乘：用非零常数k乘矩阵的任一行或任一列
3.倍加：用数k乘矩阵的任一行(列)再加到另一行(列)上

如果矩阵A经初等变换得矩阵B，则称矩阵A与矩阵B等价

初等变换性质

1.初等变换只有秩不变，其他：迹、特征值、行列式均可能改变。
理论上不改变特征值的初等变换，只有相似变换和正交变换。

---

例题1：23李林四(四)5.

分析：

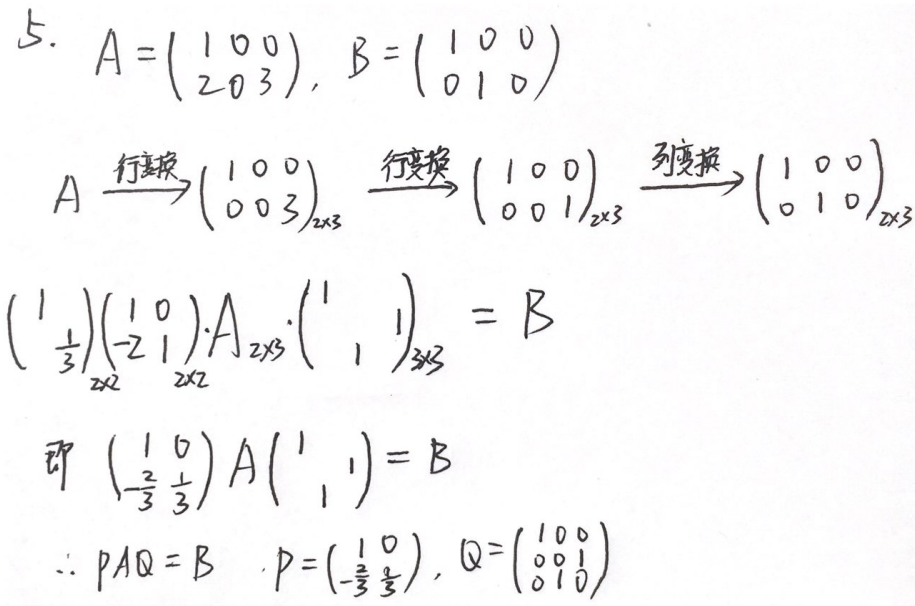
答案：D

例题2：14年13.

---

矩阵的秩

1.$r(A)=r(A^T)=r(A{A}^T)=r(A^{T}A)$

2.$r(A,B)=r(A,B{)}^T=r(\genfrac{}{}{0ex}{}{A^T}{B^T})$

3. m a x { r ( A ) , r ( B ) } ≤ r ( A , B ) ≤ r ( A + B ) max\{r(A),r(B)\}≤r(A,B)≤r(A+B) max{r(A),r(B)}≤r(A,B)≤r(A+B)

m a x { r ( A ) , r ( B ) } ≤ r ( A , B ) max\{r(A),r(B)\}≤r(A,B) max{r(A),r(B)}≤r(A,B) $\le r(A)+r(B)$

4. r ( A B ) ≤ m i n { r ( A ) , r ( B ) } r(AB)≤min\{r(A),r(B)\} r(AB)≤min{r(A),r(B)}

5.若A为m×n矩阵，矩阵的秩≤行秩，≤列秩。即 r ( A ) ≤ m i n { m , n } r(A)≤min\{m,n\} r(A)≤min{m,n}

---

例题1：18年6.

分析：矩阵是列分块的，可以作列变换而不改变矩阵的秩

A、B：(A,AB)=A(E,B)
∵r(A,b)≥r(A)，∴①r(A,AB)≥r(A)
∵r(AB)≤r(A)且r(AB)≤r(B)，∴②r(A,AB)=r[A(E,B)]≤r(A)
综上①②，r(A,AB)=r(A)
A✔B❌

C： m a x { r ( A ) , r ( ) B } ≤ r ( A , B ) ≤ r ( A ) + r ( B ) max\{r(A),r()B\}≤r(A,B)≤r(A)+r(B) max{r(A),r()B}≤r(A,B)≤r(A)+r(B) 。C❌

D：$r(A,B)=r(A,B{)}^T=r(\genfrac{}{}{0ex}{}{A^T}{B^T})$，D❌

答案：A

---

上(下)三角矩阵、对角阵

1.上(下)三角矩阵和对角阵的特征值，均为主对角线元素

可逆矩阵

可逆矩阵的定义

1.对于n阶方阵A，若存在一个n阶方阵B，使得$AB=E或BA=E$，则A、B互逆：
①$A=B^{-1}，B=A^{-1}$
②$AB=E=BA$

2.特殊情况：若$A(kB)=E$，则$kB$为A的逆矩阵

---

例题1：22年15.   乘逆矩阵，消元

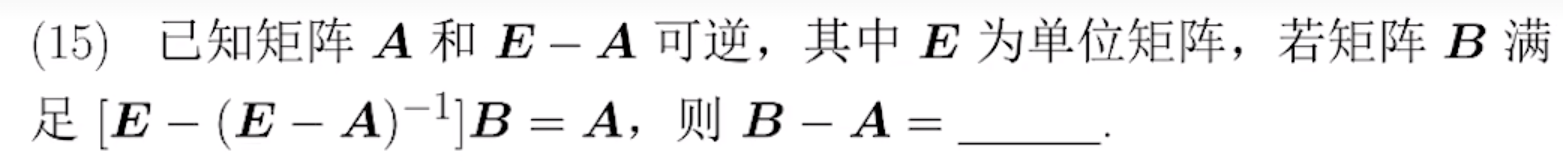
分析：
(法一)可逆矩阵的定义

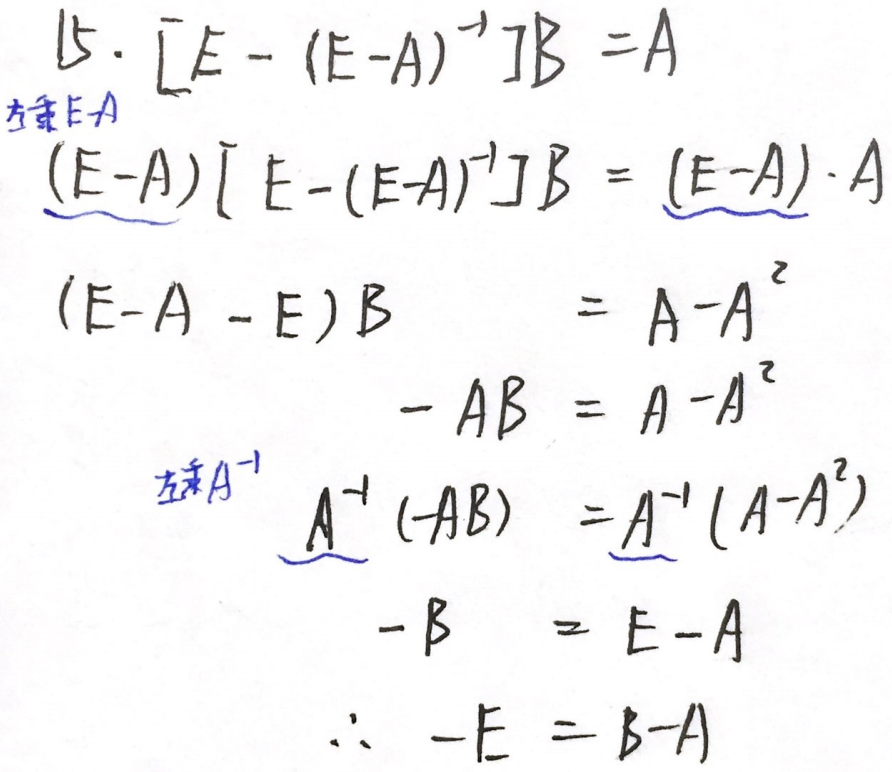
(法二)特殊值：①$令A=-E$ ②$令A=2E$ ③$令A=3E$
A取值不同，B取值也不同，但最终B-A均为-E

答案：-E

例题2：23李林四(三)15.   $AB=E=BA$

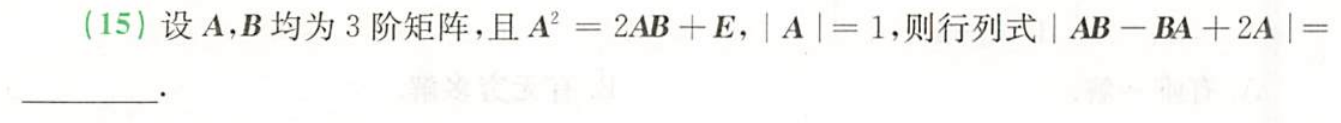
分析：
凑可逆阵：由 $A^2=2AB+E$，移项得 $A^2-2AB=E$，即$A(A-2B)=E$。
∴$A$与$A-2B$互为可逆阵，∴$A(A-2B)=(A-2B)A$，即$A^2-2AB=A^2-2BA$。即$AB=BA$。
∴$|AB-BA+2A|=|2A|=2^3|A|=8\times 1=8$

答案：8

例题3：01年4.   将等式右边变成$kE$，等式左边变成可因式分解的形式

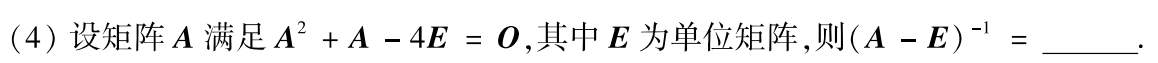
分析：由逆矩阵定义 $AB=E$ 或 $AkB=E$，找 $A-E$ 的逆矩阵。
关键在于：将等式右边变成$kE$，等式左边变成可因式分解的形式

解：由 $A^2+A-4E=O$，移项得 $A^2+A-2E=2E$
得 $(A+2E)(A-E)=2E$ $\therefore (A-E{)}^{-1}=\frac{1}{2}(A+2E)$   注意，系数要放在括号外，不要把矩阵写成分式

答案：$\frac{1}{2}(A+2E)$

例题4：08年5.   幂零阵、可逆矩阵定义、立方和公式、立方差公式

分析：由$A^3=O$得$E\pm A^3=E$
①即$E=E+A^3=(E+A)(E^2-AE+A^2)=(E+A)(E-A+A^2)$，则$E+A$可逆且$(E+A{)}^{-1}=E-A+A^2$
②即$E=E-A^3=(E-A)(E^2+AE+A^2)=(E-A)(E+A+A^2)$，则$E-A$可逆且$(E-A{)}^{-1}=E+A+A^2$

答案：C

---

可逆矩阵性质

1.若n阶方阵A可逆，则A的逆矩阵必唯一

2.若n阶方阵A可逆，则 $|A|\ne 0$

3.若n阶方阵P为可逆矩阵，则$(P^{-1}{)}^T=(P^T{)}^{-1}$

4.乘可逆矩阵，不改变原矩阵的秩

---

例题1：17年13.   乘可逆矩阵，不改变原矩阵的秩

分析：
$A=\left(\begin{array}{ccc}1& 0& 1\\ 1& 1& 2\\ 0& 1& 1\end{array}\right)\to \left(\begin{array}{ccc}1& 0& 1\\ 0& 1& 1\\ 0& 0& 0\end{array}\right)$   $\therefore r(A)=2$

矩阵$(A{\alpha }_1,A{\alpha }_2,A{\alpha }_3)=A({\alpha }_1,{\alpha }_2,{\alpha }_3)$
∵${\alpha }_1,{\alpha }_2,{\alpha }_3$线性无关   ∴$({\alpha }_1,{\alpha }_2,{\alpha }_3)$为可逆矩阵
∴$r(A{\alpha }_1,A{\alpha }_2,A{\alpha }_3)=r(A)=2$

答案：2

例题2：17年5.

---

伴随矩阵 A*

伴随矩阵的定义

若$A=\left(\begin{array}{ccc}{a}_{11}& a_{12}& a_{13}\\ a_{21}& a_{22}& a_{23}\\ a_{31}& a_{32}& a_{33}\end{array}\right)$，则$A^{\ast }=\left(\begin{array}{ccc}{A}_{11}& A_{21}& A_{31}\\ A_{12}& A_{22}& A_{32}\\ A_{13}& A_{23}& A_{33}\end{array}\right)$

伴随矩阵性质 (伴随矩阵公式)

1. $A\cdot A^{\ast }=A^{\ast }\cdot A=|A|E⇨\{\begin{array}{r}{A}^{\ast }=|A|A^{-1}\\ A^{-1}=\frac{A^{\ast }}{|A|}\end{array}$

推导：$A\cdot A^{\ast }=\left(\begin{array}{cccc}{a}_{11}& a_{12}& ...& a_{1n}\\ a_{21}& a_{22}& ...& a_{2n}\\ ...& ...& & ...\\ a_{n1}& a_{n2}& ...& a_{nn}\end{array}\right)\left(\begin{array}{cccc}{A}_{11}& A_{21}& ...& A_{n1}\\ A_{12}& A_{22}& ...& A_{n2}\\ ...& ...& & ...\\ A_{1n}& A_{2n}& ...& A_{nn}\end{array}\right)=\left(\begin{array}{cccc}|A|& & & \\ & |A|& & \\ & & ...& \\ & & & |A|\end{array}\right)$

2.$|A^{\ast }|=|A{|}^{n-1}$

推导：$A{A}^{\ast }=|A|E$   $\therefore |A{A}^{\ast }|=|A{|}^n$   $|A^{\ast }|=A^{n-1}$

3.$r(A^{\ast })=\{\begin{array}{r}n,r(A)=n\\ 1,r(A)=n-1\\ 0,r(A)<n-1\end{array}$

---

例题1：05年12.

分析：

答案：C

例题2：09年6.

分析：

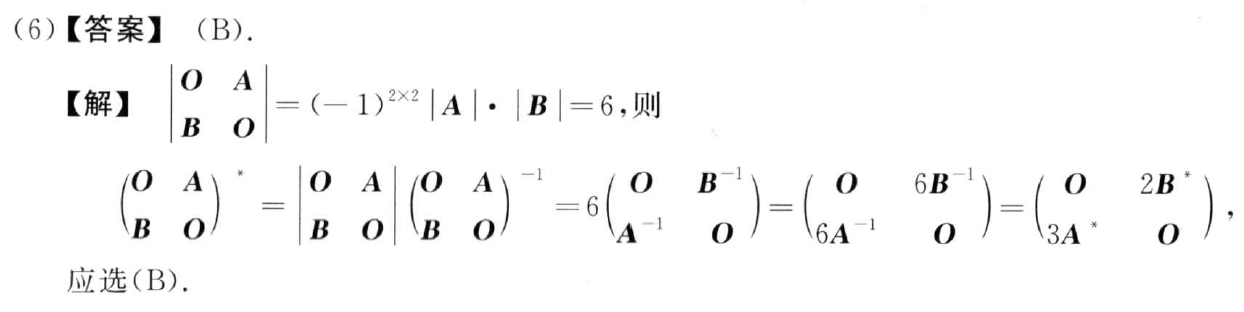
答案：B

例题3：11年6.   r(A*)的性质

分析：

答案：D

例题4：13年13.

分析：

答案：-1

---

转置矩阵

转置的性质

$(AB{)}^T=B^T{A}^T$

分块矩阵

分块矩阵的性质

1.分块矩阵的逆矩阵：
${\left(\begin{array}{cc}O& A\\ B& O\end{array}\right)}^{-1}=\left(\begin{array}{cc}O& B^{-1}\\ A^{-1}& O\end{array}\right)$

---

例题1：18年6.

---

对分块矩阵进行初等行变换

第3章 n维向量

①部分相关，整体相关
②整体无关，部分无关
③低维无关，高维无关
④高维相关，低维相关

n维单位列向量

$\alpha =\left(\begin{array}{c}{a}_1\\ a_2\\ a_3\\ ...\\ a_n\end{array}\right),{\alpha }^T=(a_1,a_2,a_3,...,a_n)$

性质：
1.$\alpha \cdot {\alpha }^T$是n×n阶方阵，${\alpha }^T\cdot \alpha$是一个数
2.$\mathrm{tr}(\alpha \cdot {\alpha }^{\mathrm{T}})={\alpha }^{\mathrm{T}}\cdot \alpha$
3.$\mathrm{r}(\alpha \cdot {\alpha }^{\mathrm{T}})=1$
4.$(\alpha \cdot {\alpha }^T{)}^T=\alpha \cdot {\alpha }^T，\therefore \alpha \cdot {\alpha }^T$是n阶实对称方阵，可以相似对角化，$\alpha \cdot {\alpha }^T\sim \left(\begin{array}{cccc}1& & & \\ & 0& & \\ & & ...& \\ & & & 0\end{array}\right)$

---

例题1：17年5.

分析：不可逆，即|A|=λ₁λ₂λ₃…=0，即有0特征值

$\alpha \cdot {\alpha }^T\sim \left(\begin{array}{cccc}1& & & \\ & 0& & \\ & & ...& \\ & & & 0\end{array}\right)$，显然 $E-\alpha \cdot {\alpha }^T$有零特征值，不可逆

答案：A

---

向量的线性关系

线性组合、线性表示

若存在常数$k_1,k_2,...,k_s,$使得$\alpha =k_1{\beta }_1+k_2{\beta }_2+...+k_s{\beta }_s，$则称向量$\alpha$是向量组${\beta }_1,{\beta }_2,...,{\beta }_s$的线性组合，或称向量$\alpha$可被向量组${\beta }_1,{\beta }_2,...,{\beta }_s$线性表示(线性表出)

---

例题1：03年10.

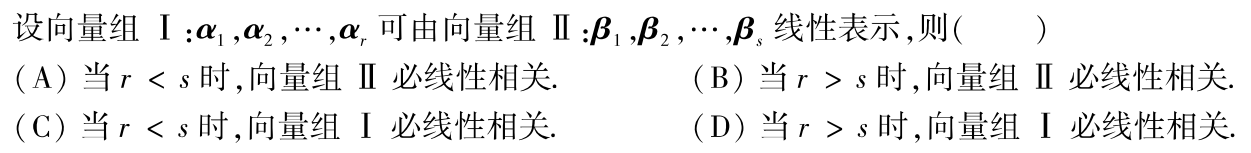
答案：D

例题2：数二 21年9.   线性表示

分析：

答案：D

例题3：20年6.   直线的点向式方程→直线的参数方程→直线参数方程的向量形式 + 线性表示

分析：

答案：C

---

线性相关

1.定义：设向量组α₁,α₂,…,α_s，若存在不全为0的数k₁,k₂,…,k_s，使k₁α₁+k₂α₂+…+k_sα_s=0，则称向量组α₁,α₂,…,α_s线性相关

2.线性相关的充要条件：α₁,α₂,…,α_s中至少有一个向量可以被其他向量线性表示

3.线性相关的等价条件：

4.线性无关可以到线性相关，若已经线性相关不可再回到线性无关

---

例题：12年05.

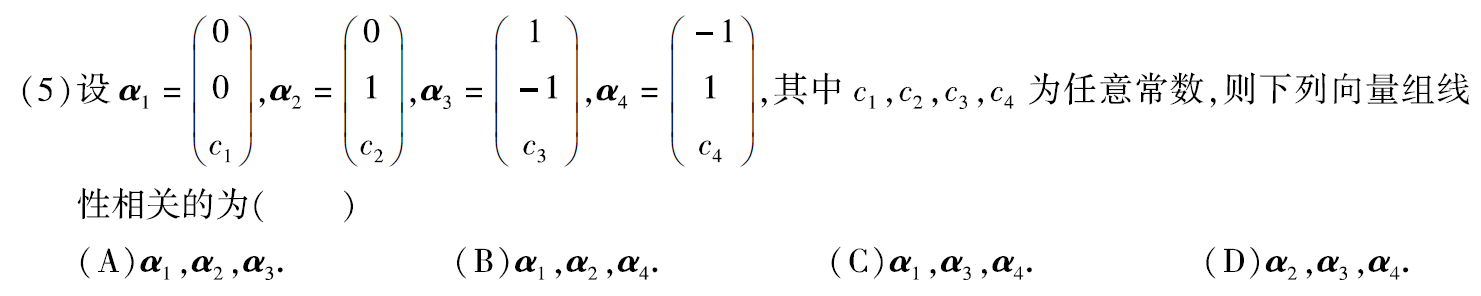
分析：
法一：线性相关的充要条件：线性相关⇦⇨行列式=0
∵|α₁,α₃,α₄|=0，∴α₁、α₃、α₄线性相关

法二：线性相关的充分条件：线性相关⇨成比例
∵α₃+α₄=(0,0,c₃+c₄)^T，与α₁成比例，∴α₁、α₃、α₄线性相关

答案：C

例题2：06年11.

分析：
若已经相关了，则初等变换后依然相关，不能再变回无关了。（若变换后是无关，则变换前肯定也得是无关）
若本来无关，通过变换可能相关。

答案：A

例题3：06年11.真题的变式

答案：C

---

线性无关

1.定义：设向量组α₁,α₂,…,α_s，若不存在不全为0(仅存在全为0)的数k₁,k₂,…,k_s，使k₁α₁+k₂α₂+…+k_sα_s=0，则称向量组α₁,α₂,…,α_s线性无关

显然，若向量组中有零向量，则向量组线性相关。(可取零向量α₀的系数k₀为任意非零常数，破坏了线性无关的定义。)
即含有零向量的向量组线性相关。
本来线性无关的向量组，加入一个零向量，它们就线性相关了。可见零向量就是一个润滑剂

2.推论：设向量组α₁,α₂,…,α_s线性无关，但向量组α₁,α₂,…,α_s,β线性相关。则向量β可由向量组α₁,α₂,…,α_s线性表示，且表示法唯一。

3.线性无关的等价条件：可逆、满秩、行列式≠0、向量组不成比例

---

例题1：14年6.   线性无关、必要性与充分性

分析：
①必要性成立，是必要条件

②充分性不成立，是非充分条件（若向量组中有一个零向量，则该向量组线性相关）

答案：A

---

矩阵等价、向量组等价

1.矩阵等价：①型同 ②秩等:R(A)=R(B)
向量组等价：①型同 ②秩等:R(A)=R(B) ③两个向量组可以相互线性表出

2.初等行变换：行向量组等价
 初等列变换：列向量组等价

---

例题1：23李林四(一)5.   向量组等价：型同、秩等、相互表出

分析：

答案：B

例题2：13年5.

答案：B

例题3：00年9.

分析：

答案：D

---

第4章 线性方程组

齐次线性方程组 Ax=0

齐次线性方程组 A_m×nx=0

---

例题：18年20.(1)

---

基础解系

1.概念：齐次方程组AX=0的解向量集合的极大线性无关组

2.表示：方程组的基础解系为${\xi }_1,{\xi }_2,...,{\xi }_{n-r}$

3.求法：
①把A化为行阶梯/行最简矩阵
②不在直角边上的 n-r(A) 个$x_i$为自由变量，设置好自由变量的值
③根据行阶梯/行最简矩阵，由最后一行倒着开始求其余变量的值，直至第一行，求出一个解向量${\xi }_1$；再从最后一行开始求，得到第二个解向量${\xi }_2$；直至求完所有解向量${\xi }_{n-r}$

自由变量

(1)谁是自由变量：化行阶梯/行最简矩阵时，不在直角边上的$x_i$为自由变量

(2)自由变量/线性无关的解向量的个数：n-r(A)

(3)自由变量的设置：
1个自由变量：1
2个自由变量：$\left(\genfrac{}{}{0ex}{}{1}{0}\right),\left(\genfrac{}{}{0ex}{}{0}{1}\right)$

3个自由变量：$\left(\begin{array}{c}1\\ 0\\ 0\end{array}\right)$，$\left(\begin{array}{c}0\\ 1\\ 0\end{array}\right)$，$\left(\begin{array}{c}0\\ 0\\ 1\end{array}\right)$

---

例题1：14年20

分析：
(2)A_3×4B_4×3=E_3×3
由于A和B都不是方阵，故AB都不可逆，更没有行列式。
考虑拆分，B=(b₁,b₂,b₃)，E=(e₁,e₂,e₃)。则AB=E被拆成Ab₁=e₁,Ab₂=e₂,Ab₃=e₃

b_i=k_iξ+特解，k为任意常数

---

方程组的通解

先求出n-r(A)个线性无关的基础解系，每一个基础解系前面加一个$k_i$，齐次方程组的通解为：$X=k_1{\xi }_1+k_2{\xi }_2+k_3{\xi }_3+...$

若非齐次方程组$AX=\beta$的特解为$\beta$，则非齐次方程组的通解为：$X=k_1{\xi }_1+k_2{\xi }_2+k_3{\xi }_3+...+\beta$

---

例题1：19年13.

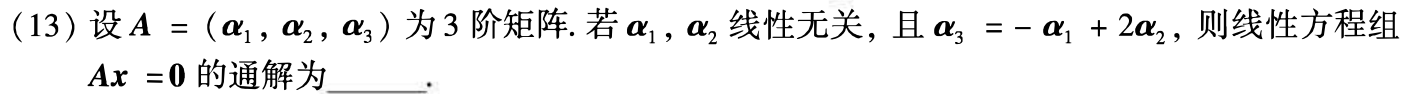
分析：

答案：$X=k\left(\begin{array}{c}1\\ -2\\ 1\end{array}\right)$，k为任意常数

---

齐次线性方程组解的判别

(1) 设A是m×n矩阵，则齐次线性方程组 AX=0 有非零解 的充要条件是 r(A)<n. 即 r(α₁,α₂,…,α_n,)<n，即 向量组α₁,α₂,…,α_n线性相关

(2) 设A是n阶方阵，则齐次线性方程组 AX=0 有非零解 的充要条件是 |A|=0

(3)设A是m×n矩阵，且m<n（行数<列数、方程组个数<未知数个数），则齐次线性方程组 AX=0 必有非零解。

非齐次线性方程组 Ax=β

非齐次线性方程组 A_m×nx=β，可组合成AX=B

非齐次线性方程组解的判别

$r(A)<r(A,\beta )$，非齐次线性方程组无解，β不能由α₁,α₂,α₃线性表示
$r(A)=r(A,\beta )$，非齐次线性方程组 AX=β有解，β可由α₁,α₂,α₃线性表示
$r(A)=r(A,\beta )=n$，方程组有唯一解，β可由α₁,α₂,α₃线性表示且表示法唯一
$r(A)=r(A,\beta )<n$，方程组有无穷多解，β可由α₁,α₂,α₃线性表示且表示法不唯一

---

例题1：23李林六套卷(二)15.

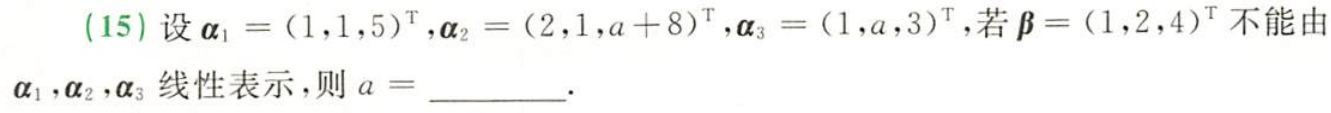
分析：β不能由α₁,α₂,α₃线性表示，即非齐次线性方程组无解，$r(A)<r(A,\beta )$

答案：0

例题2：12年20(2)

分析：
(2)Ax=β有无穷多解，则$r(A)=r(\bar{A})<n$，即r(A)<n，即 |A|=0

化为行最简后，先求齐次解Ax=0得基础解系ξ=(1,1,1,1)^T。特解即为此时的β’=(0,-1,0,0)^T。通解X=kξ+β’=k(1,1,1,1)^T+(0,-1,0,0)^T，k为任意常数

例题3：13年20.

分析：设$C=\left(\begin{array}{cc}{x}_1& x_2\\ x_3& x_4\end{array}\right)$，由AC-CA=B得出含x的方程组，写为系数矩阵D的增广矩阵$\bar{D}$，化为行最简矩阵。这时就可以通过非齐次线性方程组解的判别条件$r(D)=r(\bar{D})$来求a，b的值了。求出后把a,b代入$\bar{D}$，求出齐次方程组的基础解析${\xi }_1=\left(\begin{array}{c}1\\ -1\\ 1\\ 0\end{array}\right)$，${\xi }_2=\left(\begin{array}{c}1\\ 0\\ 0\\ 1\end{array}\right)$,非齐次通解X=$\left(\begin{array}{c}{x}_1\\ x_2\\ x_3\\ x_4\end{array}\right)=k_1{\xi }_1+k_2{\xi }_2+\left(\begin{array}{c}1\\ 0\\ 0\\ 0\end{array}\right)$

∴$C=\left(\begin{array}{cc}{x}_1& x_2\\ x_3& x_4\end{array}\right)$=…

---

同解方程组

1.定义/概念：两个方程组 $A_{m\times n}x=0$ 和 $B_{m\times n}x=0$ 有完全相同的解，则称为同解方程组

2.性质：
  $Ax=0$ 与 $Bx=0$ 为同解方程组
⇦⇨A与B的行向量组为等价向量组
⇦⇨$r(A)=r(B)=r\left(\genfrac{}{}{0ex}{}{A}{B}\right)$

---

例题1：22年6.

分析：
①仅有零解 ⇦⇨ 系数矩阵满秩
②齐次方程组的同解变形 ⇦⇨ 矩阵的初等行变换

答案：C

---

方程组的几何意义：3个方程代表3个平面，交点代表解的个数

方程组有3个方程，每个方程代表一个平面。3个平面的交点个数代表方程组的解的个数。
若三个平面相交于同一条直线，则$r(A)=r(\bar{A})=2$

---

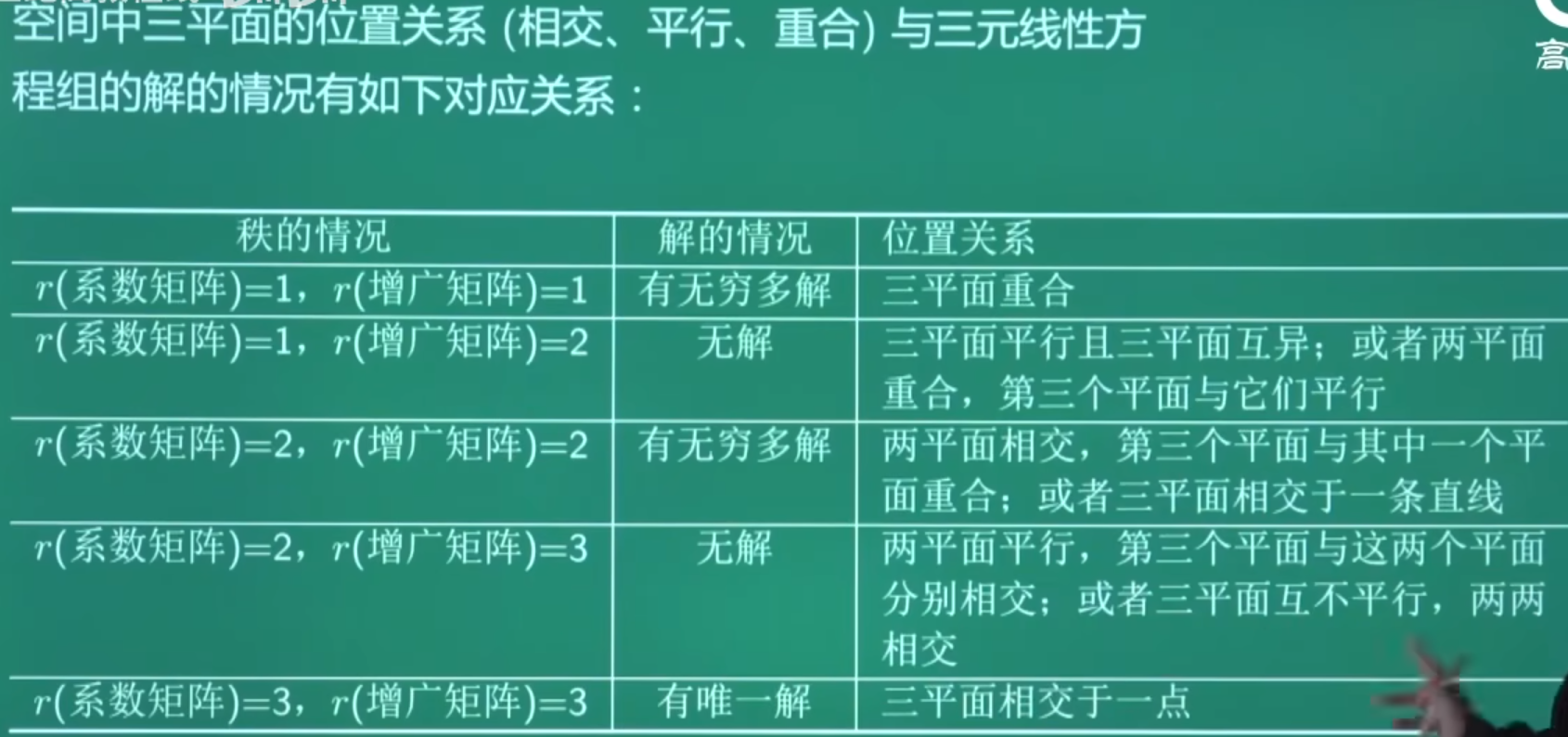
例题1：23李林六套卷(三)7.

分析：3个平面相较于一条直线，则有无穷多个交点，则$r(A)=r(\bar{A})<3$
$\bar{A}=\left(\begin{array}{cccc}1& 1& b& |3\\ 2& a+1& b+1& |7\\ 0& 1-a& 2b-1& |0\end{array}\right)$
显然，第三行要为全0，则a=1,b=1/2

答案：B

例题2：02年10.   系数矩阵秩、增广矩阵秩 用空间中的平面表示

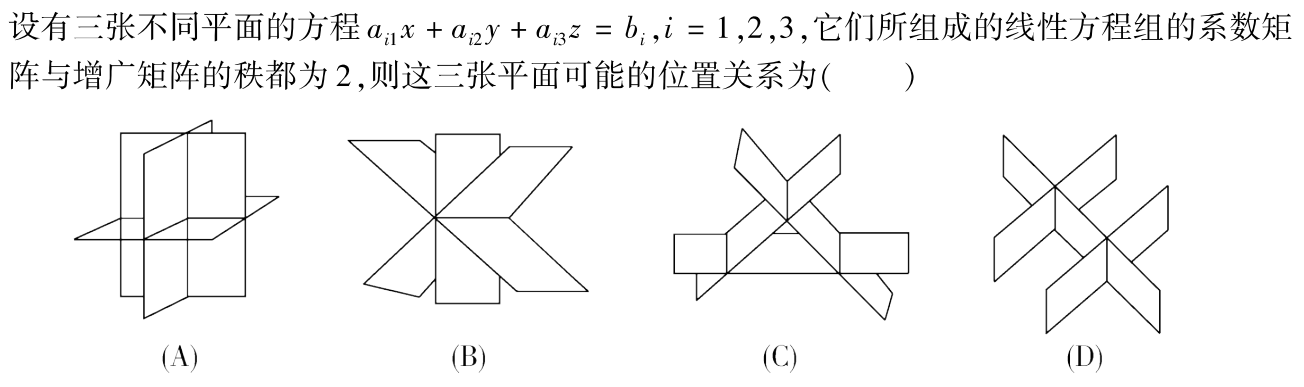
分析：
A.三个平面只有一个交点，方程组有唯一解，$r(A)=r(\bar{A})=3$。A❌
B.三个平面相较于同一条直线，即方程组有无穷多个解，$r(A)=r(\bar{A})=2<3$。B✔
C.两两相交，互不平行：$r(A)=2，r(\bar{A})=3$。 C❌
D.两平面平行，第三个平面与这两个平行平面分别相交：$r(A)=2，r(\bar{A})=3$。D❌

答案：B

例题3：19年6.

答案：A

---

第5章 相似矩阵

矩阵论

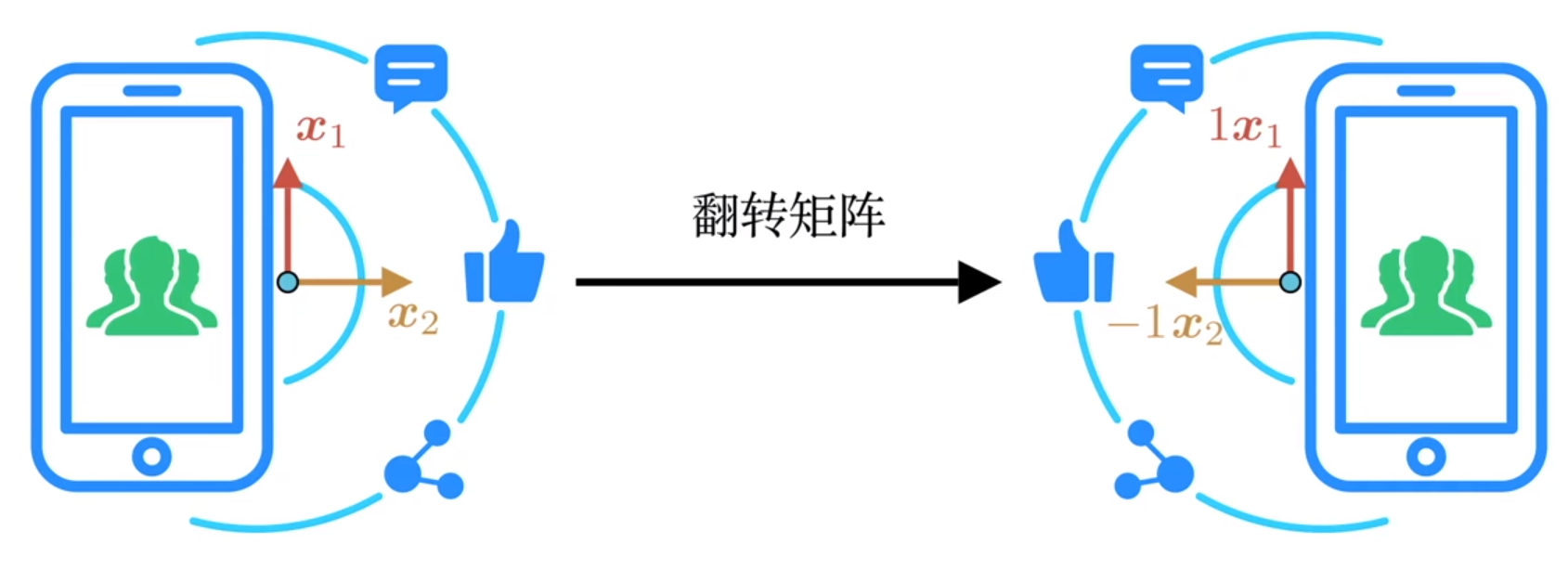
①矩阵完成的是一个向量空间到另一个向量空间的映射。
如，某向量x₁，经过矩阵A映射后，变成了Ax₁；某向量x₂，经过矩阵A映射后，变成了Ax₂。
②有些向量映射前后不在一条直线上，有些向量映射前后在一条直线上。这种映射前后在同一条直线上的向量，就称为特征向量。
③对于这种向量，矩阵只起到了伸缩作用，则Ax₂就可以表示为λx₂，这里的λ就称为矩阵A的特征值，x₂就称为此特征值对应的特征向量。
④也就是说，若非零向量x 满足 Ax=λx，那么λ被称为A的特征值，x称为A的对应于特征值λ的特征向量。Ax=λx就是特征值、特征向量的定义式。特征值λ就是非零向量
x经矩阵A映射后伸缩系数k，映射后的向量x与映射前共线，λ>0同向，λ<0反向。

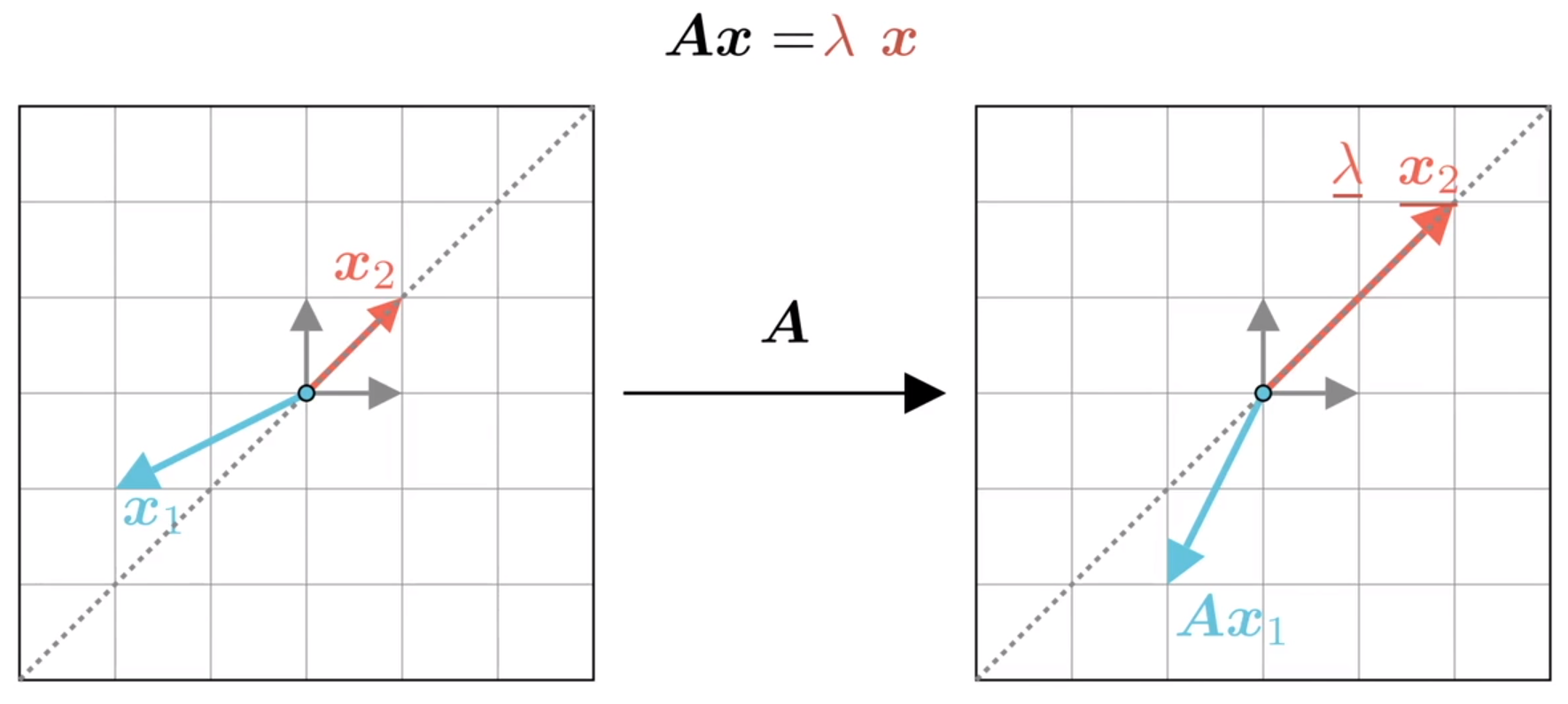
5.1 方阵的 特征值、特征向量

特征值

1.特征值定义：Ax=λx（x≠0)，则λ被称为A的特征值

若非零向量x 满足 Ax=λx，那么λ被称为A的特征值，x称为A的对应于特征值λ的特征向量

2.特征值性质：
①上/下三角矩阵的主对角线元素即为特征值
②特征值之和 = 矩阵的迹 = 主对角线元素之和，即 λ₁+λ₂+…+λ_n = tr(A) = a₁₁+a₂₂+a₃₃ + …
③特征值之积 = 矩阵的行列式，即λ₁λ₂…λ_n = |A|

矩阵主对角线元素之和称为矩阵的迹(trace)

3.特征值、特征向量对应表

矩阵	特征值	特征向量
A	λ	α
${\mathrm{A}}^{-1}$	$\frac{1}{\lambda }$	α
${\mathrm{A}}^{\ast }$	$\frac{|\mathrm{A}|}{\lambda }$	α

$A\cdot A^{\ast }=|A|E\therefore A^{\ast }=\frac{|A|}{A}\therefore$ $A^{\ast }$的特征值为$\frac{|A|}{\lambda }$

4.概念
①特征矩阵：λE-A
②特征多项式： $f(\lambda )=|\lambda E-A|$
③特征方程：f(λ)=|λE-A|=0

5.求矩阵A的特征值：
(1)|λE-A|=0
如：|λE-A|=(λ-a)(λ-b)(λ-c)=0 ∴矩阵A的特这个值为：λ₁=a，λ₂=b，λ₃=c

(2)秩为1的实对称矩阵的特征值：λ₁=tr(A)，λ₂=λ₃=0

---

例题1：18年13.

分析：A²=1，A²-1=0，(A+1)(A-1)=0，则矩阵A的特征值为1,-1。
|A|=λ₁λ₂=1×(-1)=-1

答案：-1

例题2：23李林六套卷(六)15.   特征值的性质：主对角线元素之和 = 迹 = 特征值之和

分析：A*的主对角元素为A₁₁、A₂₂、A₃₃

答案：1

---

特征向量

1.特征向量的定义： Ax=λx（x≠0)，则非零向量x被称为A的对应于特征值的特征向量

若非零向量x 满足 Ax=λx，那么λ被称为A的特征值，x称为A的对应于特征值λ的特征向量

2.特征向量的性质：
基础解系中的解向量(自由向量)的个数为 n-r(A)

3.求每个特征值对应的特征向量

5.2 矩阵的相似、相似对角化

矩阵相似

1. 相似定义

设A,B为n阶方阵，若存在可逆方阵P，使得 P^-1AP = B，则称 矩阵A与B相似，或称A,B是相似矩阵，记为A~B 。称P为A到B的相似变换矩阵或过渡矩阵。

2. 相似的必要条件 (矩阵相似的性质)：

若A、B相似，则 迹、行列式、特征值、秩相同。若可相似对角化，则相似于同一个对角阵。

若A~B，则
① tr(A)=tr(B)
② |A|=|B|
③ 特征值相同 λ₁ λ₂ λ₃ (特征值相同+实对称矩阵 → 相似)
④ 秩相等：r(A)=r(B)
⑤若A~B, 则A^-1~B^-1, A^T~B^T。证明在下面例题16年05.
⑥相似的两矩阵若均可相似对角化，则可以相似于同一个对角矩阵。该对角矩阵的主对角线元素即为特征值 λ₁、λ₂、λ₃
⑦A~B，则A等价于B，即A可通过初等变换化为B

---

例题1：15年21.(1)、20年20.(1)

$\because A\sim B\therefore \{\begin{array}{c}tr(A)=tr(B)\\ |A|=|B|\end{array}$

例题2：16年05.

分析：需要掌握相似性质的证明
已知A~B，则若存在可逆矩阵P使得P^-1AP = B。此题额外附加了A、B均为可逆矩阵的条件
①证明：A^-1~B^-1
∵P^-1AP = B
对两边取逆
得 P^-1A^-1P = B^-1，即A^-1~B^-1

②证明：A^T~B^T
∵P^-1AP=B
对两边取转置
得 P^TA^T(P^-1)^T = B^T
即 [(P^T)^-1]^-1A^T(P^T)^-1 = B^T
令Q = (P^T)^-1 = (P^-1)^T，则 Q^-1A^TQ = B^T，则 A^T~B^T

③在此题A、B均为可逆矩阵的前提下，D正确
P^-1AP = B
P^-1A^-1P = B^-1
∴P^-1(A+A^-1)P = B+B^-1

④C，需要A、B均为实对称矩阵

答案：C

---

3. 两个 实对称/可相似对角化 的矩阵相似的充要条件：

两实对称矩阵/两可相似对角化的矩阵 相似 ⇦⇨ 特征多项式相同 ⇦⇨ 特征值全部相同

对于普通矩阵来说，特征多项式相同、特征值相同，只是相似的必要条件。
但对于两个 实对称/可对角化 的矩阵 来说，特征多项式相同、特征值相同等相似的必要条件，就变成了相似的充分必要条件。

证明：
1.若A、B均可相似对角化，且A、B特征值相同，则A、B相似于同一个对角阵。则$P^{-1}AP=\Lambda ，A\sim \Lambda P^{-1}BP=\Lambda ，B\sim \Lambda$
由相似的传递性，可知$A\sim \Lambda \sim B，\therefore A\sim B$

2.若A、B均为实对称矩阵。实对称矩阵一定可以相似对角化，再接1的证明

条件由强到弱依次是：
①实对称
②不对称但可相似对角化
③不对称，也不可相似对角化

4. 非实对称矩阵相似

(1)充要条件：若两矩阵相似，则特征矩阵也相似，则特征矩阵的秩相等。即 $A\sim B⇦⇨kE-A\sim kE-B$
(2)必要条件：A~B → r(A)=r(B)
λE-A ~ λE-B → r(λE-A) = r(λE-B)

证明：

---

例题1：18年5.

分析：
显然，M、A、B、C、D的特征值均为1，1，1。$M\sim A⇦⇨kE-M\sim kE-A\to r(kE-M)=r(kE-A)$
r(E-M)=2，r(E-A)=2，r(E-B)=r(E-C)=r(E-D)=1，∴E-M~E-A

答案：A

例题2：13年06.   实对称矩阵相似的充要条件：特征值相同

分析：

答案：B

---

相似对角化

对角化的定义

$P^{-1}AP=\Lambda =\left(\begin{array}{ccc}{\lambda }_1& & \\ & {\lambda }_2& \\ & & {\lambda }_3\end{array}\right)，A\sim \Lambda$

n阶矩阵A可相似对角化的条件

n阶矩阵A可相似对角化的条件
充分条件	①A为实对称矩阵
	②A有n个互异的特征值
充要条件	①A有n个线性无关的特征向量
	②A的每一个k重特征值，都有k个线性无关的特征向量 【2重根,要有2个线性无关的特征向量，n-r(λE-A)=3-1=2 ∴r(λE-A)=1】

---

例题1：17年6.   相似对角化的条件

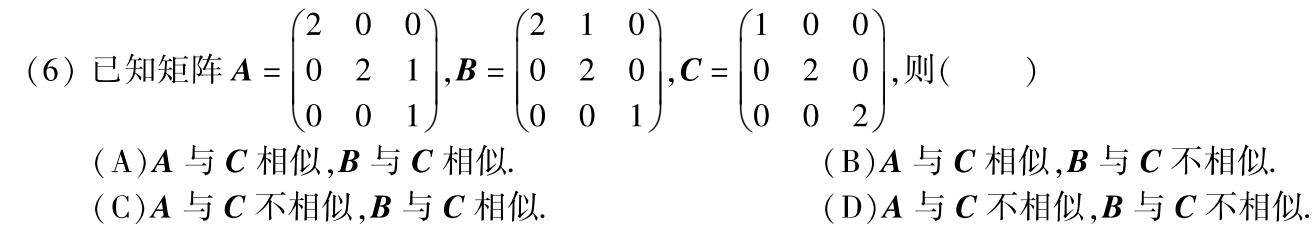
分析：
A、B为上三角矩阵，C为对角矩阵。显然，A、B、C的特征值均为 2，2，1。
判断A、B是否与C相似， 即A、B能否相似对角化。
由相似对角化的充要条件：2重根,要有2个线性无关的特征向量，n-r(λE-A)=3-1=2 ∴r(λE-A)=1

显然，r(2E-A)=1，而r(2E-B)=2，∴A可以相似对角化，B不可以

答案：B

例题2：15年21.(2)

求可逆矩阵P，使P^-1AP为对角矩阵：
只需求出其特征值，以及对应的n个线性无关的特征向量即可

分析：
①求特征值：A~B，∴A和B特征值相同。因为B的0更多，特征值更好求，所以用矩阵B来求特征值。
②求特征向量：分别将3个特征值λ代入λE-A，化简矩阵，得线性无关的特征向量

解题步骤：
①|λE-B|= |三阶行列式| =(λ-1)²(λ-5) ∴B的特征值为1，1，5
∵A~B ∴A的特征值也为1，1，5

②将λ=1代入(λE-A)x=0，即(E-A)x=0
E-A =()→()，得A的属于特征值λ=1的线性无关的特征向量为α₁=( )，α₂=( )

将λ=5代入(λE-A)x=0，即(5E-A)x=0
5E-A=()→()，得A的属于特征值λ=5的线性无关的特征向量为α₃=( )

令P=(α₁,α₂,α₃)，则P^-1AP = ʌ =()

例题3：19年21.(2)

例题4：20年20.(2)

---

5.3实对称矩阵的对角化

实对称矩阵的性质

1.实对称矩阵必能相似对角化
2.实对称矩阵必有n个线性无关的特征向量
3.实对称矩阵 不同特征值对应的特征向量一定正交

---

例题1：23李林四(一)6.

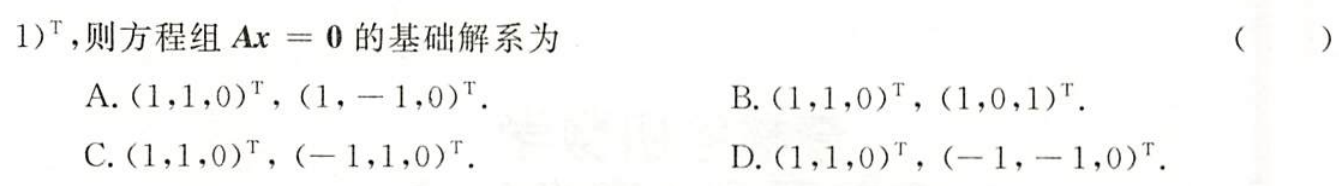
分析：

答案：B

---

正交矩阵、正交变换

正交矩阵Q

1.正交矩阵定义：$Q{Q}^T=Q^{T}Q=E$

2.正交矩阵性质：：(A,B均为n阶正交矩阵)
(1) $Q^{-1}=Q^T$
(2) Q的各行向量两两正交，各列向量两两正交
(3)$|Q|=\pm 1$
(4)$A^{-1}、A^T、AB$也是正交阵
(5)方阵A是正交矩阵的充要条件：Q的列向量组或行向量组为标准正交向量组

3.求正交矩阵Q，使得${\mathrm{Q}}^{\mathrm{T}}\mathrm{AQ}$为对角矩阵：
①求A的特征值：即求A的特征方程|λE-A|=0的全部解
②求A的特征向量：对求得的每一个特征值，将其代入$(\lambda E-A)x=0$，求出每个特征值对应的特征向量
③特征向量正交化
④特征向量单位化。然后组成正交矩阵Q

施密特正交化

取
${\beta }_1={\alpha }_1$

${\beta }_2={\alpha }_2-\frac{({\alpha }_2,{\beta }_1)}{({\beta }_1,{\beta }_1)}{\beta }_1$

${\beta }_3={\alpha }_3-\frac{({\alpha }_3,{\beta }_1)}{({\beta }_1,{\beta }_1)}{\beta }_1-\frac{({\alpha }_3,{\beta }_2)}{({\beta }_2,{\beta }_2)}{\beta }_2$
…
${\beta }_n={\alpha }_n-\frac{({\alpha }_n,{\beta }_1)}{({\beta }_1,{\beta }_1)}{\beta }_1-\frac{({\alpha }_n,{\beta }_2)}{({\beta }_2,{\beta }_2)}{\beta }_2-...-\frac{({\alpha }_n,{\beta }_{n-1})}{({\beta }_{n-1},{\beta }_{n-1})}{\beta }_{n-1}$

向量积(叉乘)得与两向量都垂直的向量

$c=a\times b=\left|\begin{array}{ccc}\vec{i}& \vec{j}& \vec{k}\\ a_x& a_y& a_z\\ b_x& b_y& b_z\end{array}\right|$

---

例题1：22年21.(2)   ①二次型的定义 ②求正交矩阵、正交变换法化二次型为标准型 ③配方法

答案：

例题2：20年20(2)

---

正交变换

1.定义：若Q为正交矩阵，则线性变换x=Qy称为正交变换。正交变换属于相似变换，不改变矩阵的特征值。

2.性质：
(1)正交变换保持向量的内积不变
(2)正交变换保持向量的长度不变
(3)正交变换保持向量的夹角不变

正交变换，既相似又合同

---

例题1：11年13.   正交变换不改变矩阵的特征值、行列式=特征值之积

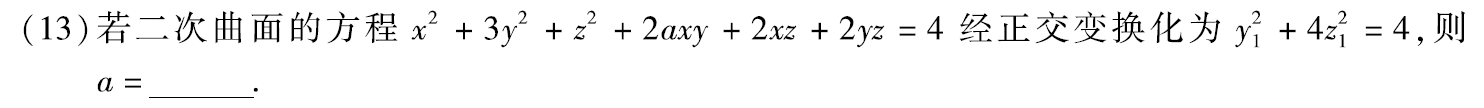
分析：

答案：1

---

实对称矩阵的对角化

1.实对称矩阵的相似对角化：
(1)实对称矩阵的特征值都是实数
(2)实对称矩阵A的不同特征值对应的特征向量一定正交
(3)实对称矩阵必有n个线性无关的特征向量
(4)实对称矩阵必能相似对角化
(5)非零的幂零矩阵一定不能相似对角化

2.对于任一n阶实对称矩阵A，必存在正交矩阵Q，使得$$Q^{-1}AQ=Q^{T}AQ=\Lambda =\left(\begin{array}{cccc}{\lambda }_1& & & \\ & {\lambda }_2& & \\ & & ...& \\ & & & {\lambda }_n\end{array}\right)$$
其中${\lambda }_1,{\lambda }_2,...,{\lambda }_n$为A的n个实特征值，矩阵Q的列向量为A的依次对应于${\lambda }_1,{\lambda }_2,...,{\lambda }_n$的两两正交的单位特征向量

3.根据上述结论，总结出正交变换矩阵Q将实对称矩阵A对角化的步骤为：
(1)求出A的全部特征值${\lambda }_1,{\lambda }_2,...,{\lambda }_n$
(2)对每个特征值${\lambda }_i$，求出其特征向量
(3)将特征向量正交化，再单位化
(4)将这些单位向量作为列向量构成正交矩阵Q，从而有$Q^{-1}AQ=Q^{T}AQ=\Lambda =\left(\begin{array}{cccc}{\lambda }_1& & & \\ & {\lambda }_2& & \\ & & ...& \\ & & & {\lambda }_n\end{array}\right)$

第6章 二次型

二次型定义

二次型的矩阵表达式：$f(x)=x^{T}Ax$
A为实对称矩阵，称为二次型的系数矩阵。

---

例题1：23李林六套卷(五)15.   二次型定义、合同的定义及性质

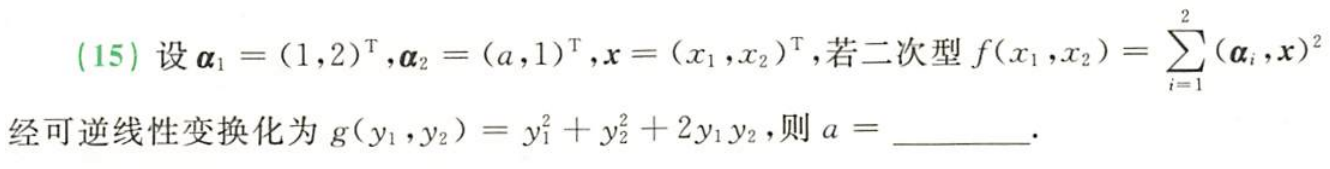
答案：

---

二次型与矩阵的对应关系

1.看到二次型能写出矩阵，看到矩阵能写出它的二次型。
2.二次型f的矩阵，就是A，不能带x。二次型的定义是$f(x)=x^{T}Ax$

---

例题1：02年4.

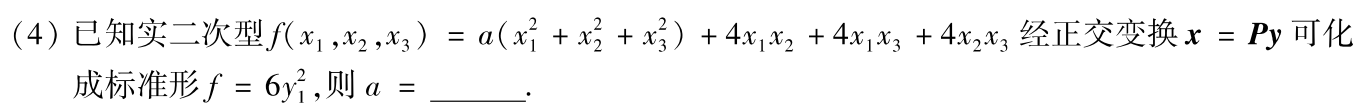
分析：对二次型进行正交变换得标准形，实际上就是对矩阵进行相似对角化。正交变换得到的标准形对应矩阵都是对角矩阵，标准形系数都是特征值。

答案：2

---

二次型与二次曲面

---

例题1：16年06.  二次型与二次曲面

分析：

答案：B

---

合同

1.合同的定义：设A,B为n阶方阵，若存在可逆矩阵C，使得$B=C^{T}AC$，则称 矩阵A与B合同

2.合同的性质：两合同矩阵的正负特征值个数相同
$A、B合同⇦⇨A、B有相同的正、负惯性指数⇦⇨A、B有相同的正惯性指数和相同的秩$

相似与合同

(实对称矩阵)相似→合同：(实对称矩阵)相似 ⇨ 特征值相同 ⇨ 正负特征值个数一定相同 ⇨ 合同

---

例题1：07年8.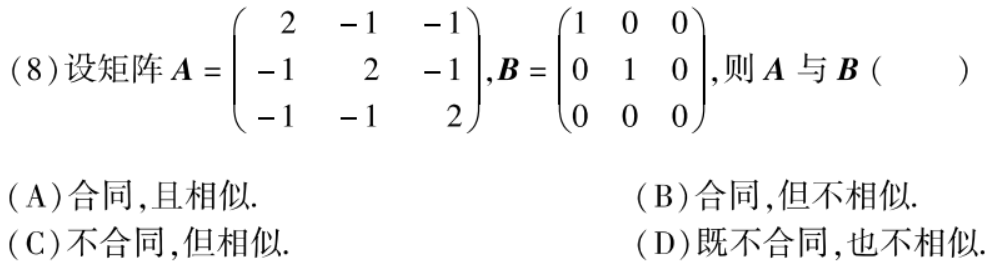

分析：相似还是合同，只需要看特征值

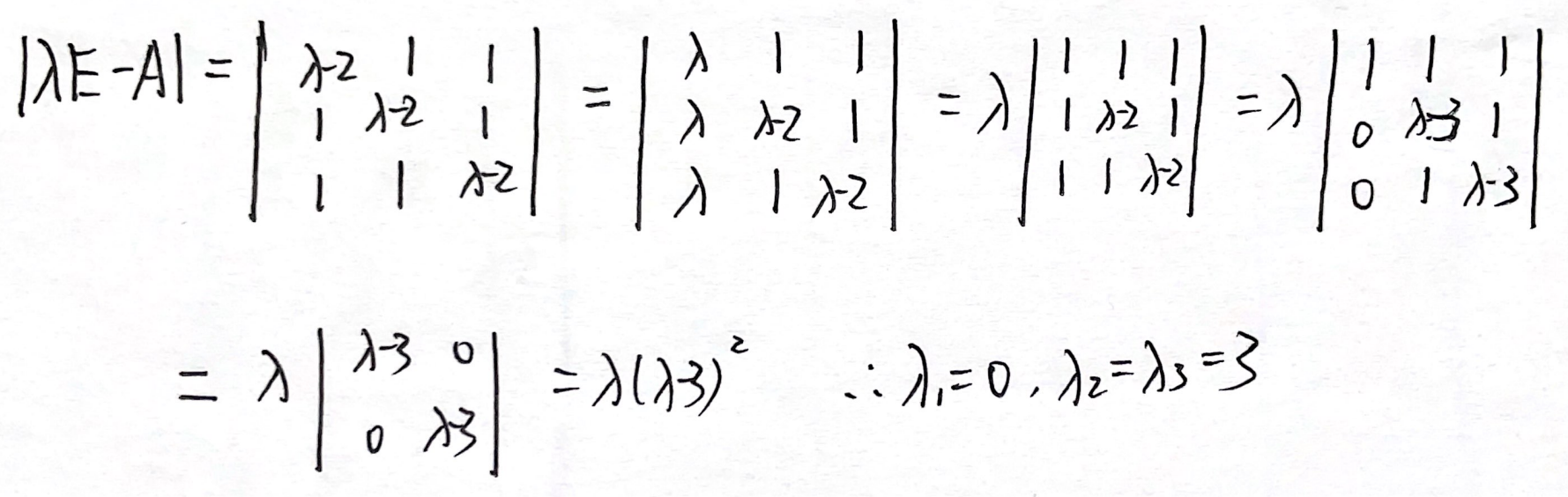
由|λE-A|=0求得A的特征值为3,3,0。对角阵B的特征值为1,1,0。可见AB特征值不相同，不相似。但是 正惯性指数和秩相同，因此AB合同。

答案：B

例题2：01年9.

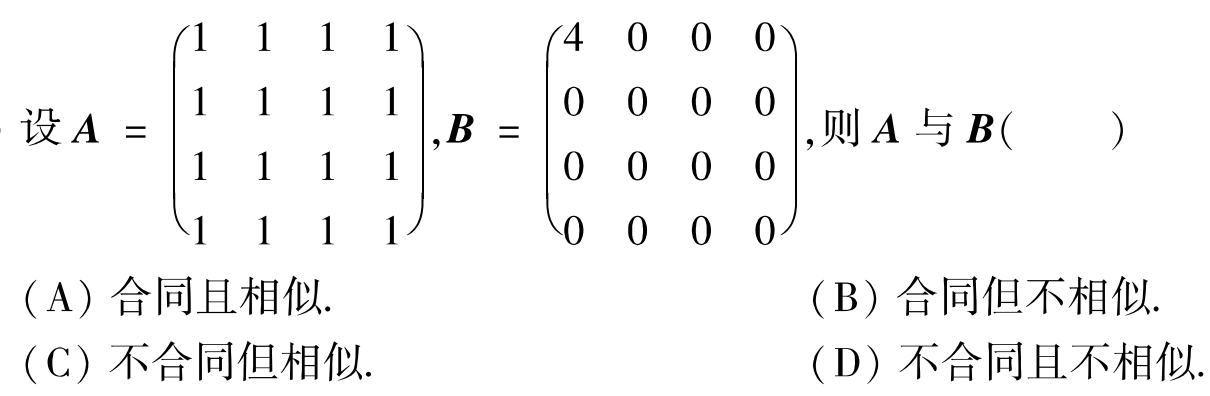
分析：A、B均为实对称矩阵
由|λE-A|=0求得A的特征值为 λ₁=4,λ₂=λ₃=λ₄=0
对角阵B的特征值也为λ₁=4,λ₂=λ₃=λ₄=0
特征值相同，∴A、B相似。
特征值相同，则正负惯性指数也必然相同，∴A、B合同

答案：A

---

标准形

1.与对角矩阵对应的二次型f( 只含有平方项)，即为标准型。

可逆线性变换 x=cy

正交变换法 化二次型为标准形：得对角阵，系数为特征值

1.定理：任意给定实二次型 $f=x^{T}Ax(A^T=A)$，一定存在正交变换 x=Qy，使f 化为标准形 $f={\lambda }_1{y}_1^2+{\lambda }_2{y}_2^2+...+{\lambda }_n{y}_n^2$ 。其中λ_i(i=1,2,…,n)为二次型矩阵A的特征值。

2.性质：正交变换也是相似变换。正交变换前后的两个矩阵一定相似

3.用正交变换化二次型为标准形的步骤：
(1)写出二次型对应的实对称矩阵A
(2)求出A的所有特征值和特征向量
(3)将特征向量正交化、单位化，得η₁,η₂,…,η_n,
(4)取Q=(η₁,η₂,…,η_n)，作正交变换 x=Qy，得f的标准形

---

例题1：15年6.

分析：

答案：A

例题2：20年20.

分析：
(1)①二次型与矩阵的对应关系 ②正交变换也是相似变换
(2) ∵二阶矩阵A、B均有2个互异的特征值，∴A、B均可相似对角化
且∵A~B，∴A、B相似于同一个对角矩阵

设A ~ Λ，则存在可逆矩阵P₁使得 $P_1^{-1}A{P}_1=\Lambda$
设B ~ Λ，则存在可逆矩阵P₂使得 $P_2^{-1}B{P}_2=\Lambda$
$\therefore B=P_2\Lambda P_2^{-1}=P_2{P}_1^{-1}A{P}_1{P}_2^{-1}$
令$P=P_1{P}_2^{-1}$，$\therefore B=P^{-1}AP$

所以，求出P₁、P₂，得$P=P_1{P}_2^{-1}$。对P进行正交化单位化，得正交矩阵Q

例题3：12年21.

分析：秩的性质、正交变换的步骤

答案：(1)a = -1

---

配方法 化二次型为标准形

---

例题1：14年13.   配方法求二次型的标准形

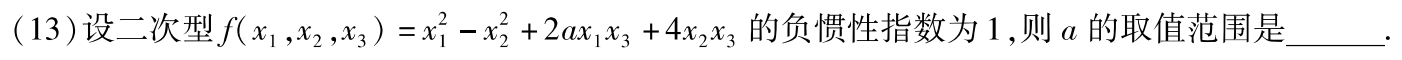
分析：初等变换改变特征值，相似变换不改变特征值

答案：[-2,2]

---

正定二次型

规范形

标准形：平方项的系数为特征值？？？（好像不一定，配方法不一定，只有正交变换法得到的才是特征值。因为正交变换法是得到了对角阵）
规范形：平方项的系数为+1或-1

---

例题：18年20(2)   线性方程组、规范形

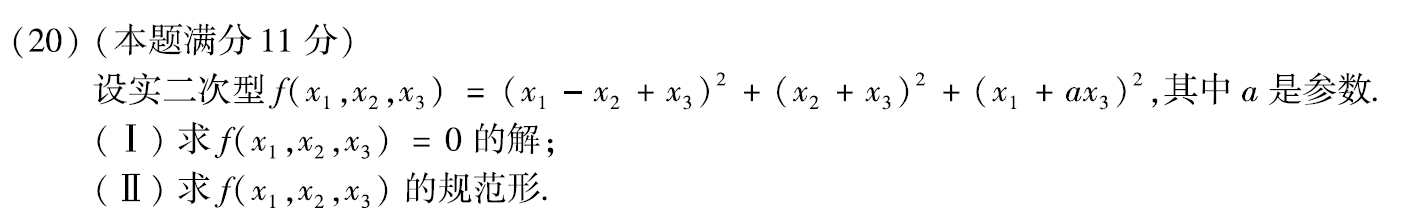
分析：
(1)平方和为0，则每个括号内都为0
(2)

---

惯性定理

正负惯性指数

1.正惯性指数：正特征值的个数
2.负惯性指数：负特征值的个数。满秩时，负惯性指数为奇数，行列式<0

---

例题：14年13.

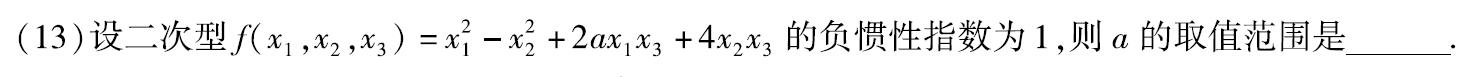
分析：
求特征值时，不可进行初等变换(初等变换会改变特征值)，不要化为行最简。此题直接求特征值困难。
满秩时，负惯性指数为奇数，行列式<0

答案：[-2,2]

---

正定矩阵

概念 (二次型正定性的判别)

设 f=x^TAx (A^T=A)为实二次型，若对于任意非零向量x，
(1)恒有 x^TAx >0，则称 f=x^TAx 为正定二次型，称矩阵A为正定矩阵；
恒有 x^TAx <0，则称f=x^TAx 为负定二次型，称矩阵A为负定矩阵；
(2)恒有 x^TAx ≥ 0，则称 f=x^TAx为 半正定二次型，称矩阵A为半正定矩阵；
恒有 x^TAx ≤ 0，则称 f=x^TAx为 半负定二次型，称矩阵A为半负定矩阵；
(3)若f=x^TAx的值时而为正，时而为负，则称 f=x^TAx 为不定二次型

性质

矩阵A正定
⇦⇨对任意非零n位列向量 $x$，总有 $f=x^{T}Ax>0$ (正定的定义)
⇦⇨A的特征值均为正值
⇦⇨A的正惯性指数 $p=r=n$
⇦⇨A的各阶顺序主子式全大于零 (从左上角或右下角开始都可)
⇦⇨A与单位阵E合同，即 $P^{T}AP=E$
⇦⇨存在可逆矩阵Q，使得 $A=Q^{T}Q$

第7章 向量空间 （数一）

向量空间的概念

基

向量空间的基的2个必要条件：设V为向量空间，若r个向量α₁,α₂,…,α_r∈V，且满足
(1)α₁,α₂,…,α_r线性无关
(2)V中任意向量都可由α₁,α₂,…,α_r线性表示
则向量组α₁,α₂,…,α_r称为向量空间V的一个基，r称为向量空间V的维数，并称V为r维向量空间

基的概念类似极大线性无关组、基础解系
若把向量空间V看作向量组，则由极大线性无关组的等价定义可知，V的基就是向量组的极大无关组，V的维数就是向量组的秩。

证明向量组为R³的基，只需要证明向量组中各向量线性无关

---

例题：15年20(1)

---

过渡矩阵（基变换）

求A基到B基的过渡矩阵：（右乘列变换）
AP=B，则过渡矩阵 P=A^-1B

---

例题1：03年4.

分析：$AP=B\therefore P=A^{-1}B$

答案：$\left(\begin{array}{cc}2& 3\\ -1& -2\end{array}\right)$

例题2：19年20.

分析：
(1)

(2)
①证明3个向量是R³的基，只需证明它们线性无关 [向量的基线性无关]
②求A基到B基的过渡矩阵：
AP=B，则过渡矩阵 P=A^-1B

答案：

---

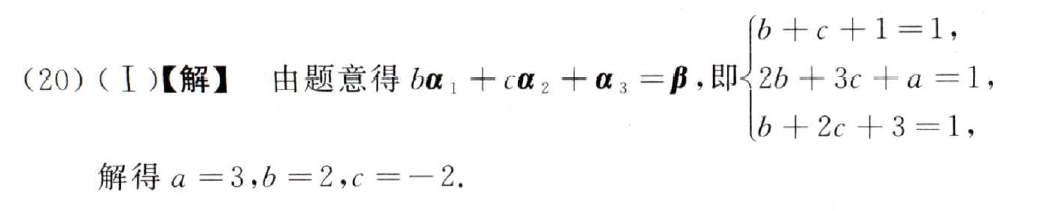
向量在基下的坐标

向量 = 基·坐标_列向量 ⇨ 坐标_列向量=(基)^-1·向量
$\alpha =({\alpha }_1,{\alpha }_2,{\alpha }_3)\left(\begin{array}{c}{x}_1\\ x_2\\ x_3\end{array}\right)={\alpha }_1{x}_1+{\alpha }_2{x}_2+{\alpha }_3{x}_3$

∴坐标_列向量=$\left(\begin{array}{c}{x}_1\\ x_2\\ x_3\end{array}\right)=({\alpha }_1,{\alpha }_2,{\alpha }_3{)}^{-1}\cdot \alpha$

∴$坐标=(x_1,x_2,x_3)$

---

例题1：23李林四(二)15.

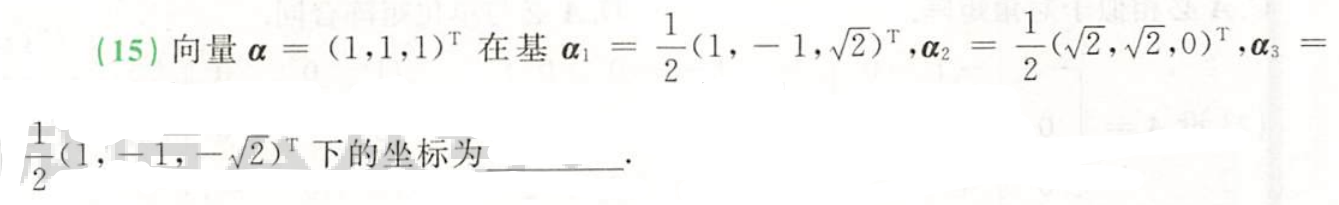
分析：

答案：$(\frac{\sqrt{2}}{2},\sqrt{2},-\frac{\sqrt{2}}{2})$

例题2：15年20.

分析：
(1)证明向量组是R³的一个基，只需要证明向量组线性无关
(2)坐标

---