您现在的位置是：首页 > 其他

当前栏目

LeetCode动态规划基础题-子字符串问题(13题)

LeetCode 规划基础字符串动态 13 问题

2023-09-11 14:20:00 时间

前言

觉得有帮助的，要不三连一下~
在这里插入图片描述
既然不能出去玩，那还是来学习吧。

一、子字符串问题

1 最长递增子序列

300.最长递增子序列

力扣题目链接(opens new window)

给你一个整数数组 nums ，找到其中最长严格递增子序列的长度。

子序列是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序。例如，[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。

示例 1：输入：nums = [10,9,2,5,3,7,101,18] 输出：4 解释：最长递增子序列是 [2,3,7,101]，因此长度为 4 。

示例 2：输入：nums = [0,1,0,3,2,3] 输出：4

示例 3：输入：nums = [7,7,7,7,7,7,7] 输出：1

提示：

1 <= nums.length <= 2500
-10^4 <= nums[i] <= 104

dp数组的定义

dp[i]表示i之前包括i的以nums[i]结尾最长上升子序列的长度

状态转移方程

位置i的最长升序子序列等于j从0到i-1各个位置的最长升序子序列 + 1 的最大值。

if (nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1);

初始化
遍历顺序
距离说明

300.最长上升子序列

class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        if (nums.size() <= 1) return nums.size();
        vector<int> dp(nums.size(), 1);
        int result = 0;
        for (int i = 1; i < nums.size(); i++) {
            for (int j = 0; j < i; j++) {
                if (nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1);
            }
            if (dp[i] > result) result = dp[i]; // 取长的子序列
        }
        return result;
    }
};

2 最长连续递增序列

最长连续递增序列

给定一个未经排序的整数数组，找到最长且连续递增的子序列，并返回该序列的长度。

连续递增的子序列可以由两个下标 l 和 r（l < r）确定，如果对于每个 l <= i < r，都有 nums[i] < nums[i + 1] ，那么子序列 [nums[l], nums[l + 1], …, nums[r - 1], nums[r]] 就是连续递增子序列。

示例 1：输入：nums = [1,3,5,4,7] 输出：3 解释：最长连续递增序列是 [1,3,5], 长度为3。尽管 [1,3,5,7] 也是升序的子序列, 但它不是连续的，因为 5 和 7 在原数组里被 4 隔开。

示例 2：输入：nums = [2,2,2,2,2] 输出：1 解释：最长连续递增序列是 [2], 长度为1。

提示：

0 <= nums.length <= 10^4
-10^9 <= nums[i] <= 10^9

与上一题最大的区别就是连续二字

确定dp数组（dp table）以及下标的含义

dp[i]：以下标i为结尾的数组的连续递增的子序列长度为dp[i]。

确定递推公式

如果 nums[i + 1] > nums[i]，那么以 i+1 为结尾的数组的连续递增的子序列长度一定等于以i为结尾的数组的连续递增的子序列长度 + 1 。

for (int i = 0; i < nums.size() - 1; i++) {
    if (nums[i + 1] > nums[i]) { // 连续记录
        dp[i + 1] = dp[i] + 1; // 递推公式
    }
}

初始化
遍历舒徐
举例分析

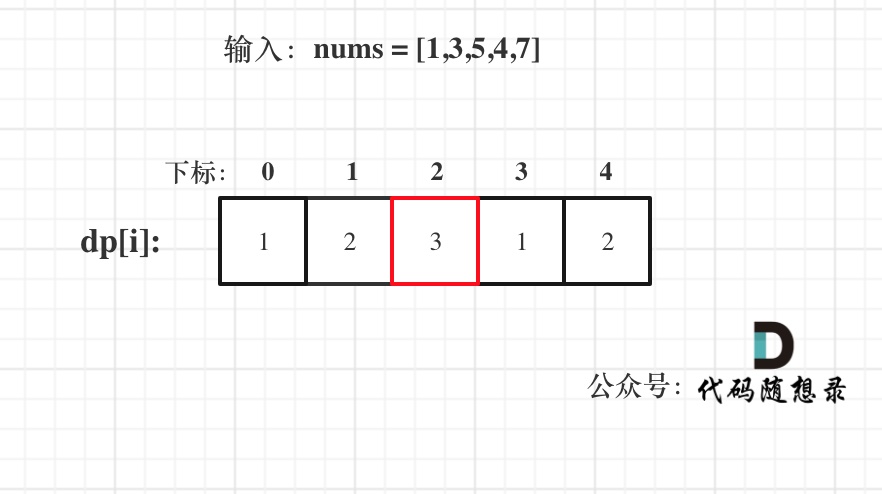
674.最长连续递增序列

class Solution {
public:
    int findLengthOfLCIS(vector<int>& nums) {
        int n = nums.size();
        if(n<=1) return n;
        vector<int> dp(n,1);
        int res = 0;
        for(int i = 1; i < n; ++i){
            if(nums[i] > nums[i-1]){
                dp[i] = dp[i-1] + 1;
            }
            //cout<<dp[i]<<" ";
            res = max(res, dp[i]);
        }
        return res;
    }
};

3 最长重复子数组

最长重复子数组

给两个整数数组 A 和 B ，返回两个数组中公共的、长度最长的子数组的长度。

示例：

输入： A: [1,2,3,2,1] B: [3,2,1,4,7] 输出：3 解释：长度最长的公共子数组是 [3, 2, 1] 。

提示：

1 <= len(A), len(B) <= 1000
0 <= A[i], B[i] < 100

这道题基本上就是上课讲动态规划的经典例题了。

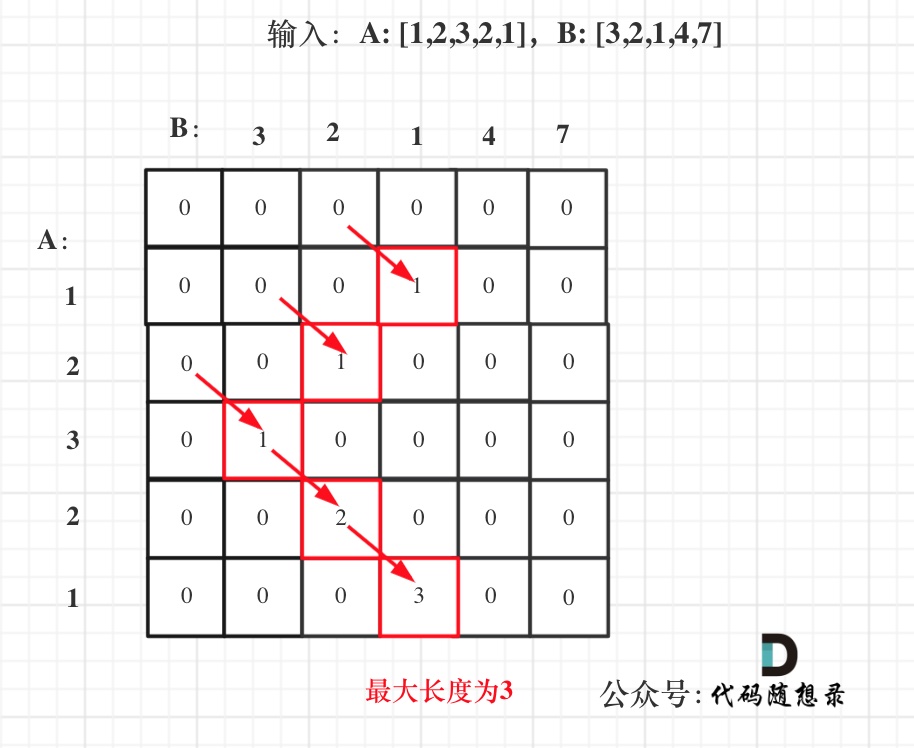
718.最长重复子数组

确定dp

以下标i - 1为结尾的A，和以下标j - 1为结尾的B，最长重复子数组长度为dp[i][j]。

确定递推公式

dp[i][j] = dp[i - 1][j - 1] + 1;

for (int i = 1; i <= A.size(); i++) {
    for (int j = 1; j <= B.size(); j++) {
        if (A[i - 1] == B[j - 1]) {
            dp[i][j] = dp[i - 1][j - 1] + 1;
        }
        if (dp[i][j] > result) result = dp[i][j];
    }
}

dp数组如何初始化

dp[1][1] = dp[0][0] + 1，只有dp[0][0]初始为0

遍历顺序
举例推导

class Solution {
public:
    int findLength(vector<int>& A, vector<int>& B) {
        vector<vector<int>> dp (A.size() + 1, vector<int>(B.size() + 1, 0));
        int result = 0;
        for (int i = 1; i <= A.size(); i++) {
            for (int j = 1; j <= B.size(); j++) {
                if (A[i - 1] == B[j - 1]) {
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                }
                if (dp[i][j] > result) result = dp[i][j];
            }
        }
        return result;
    }
};

滚动数组

718.最长重复子数组

我们可以看出dp[i][j]都是由dp[i - 1][j - 1]推出。那么压缩为一维数组，也就是dp[j]都是由dp[j - 1]推出。

也就是相当于可以把上一层dp[i - 1][j]拷贝到下一层dp[i][j]来继续用。

此时遍历B数组的时候，就要从后向前遍历，这样避免重复覆盖。

class Solution {
public:
    int findLength(vector<int>& A, vector<int>& B) {
        vector<int> dp(vector<int>(B.size() + 1, 0));
        int result = 0;
        for (int i = 1; i <= A.size(); i++) {
            for (int j = B.size(); j > 0; j--) {
                if (A[i - 1] == B[j - 1]) {
                    dp[j] = dp[j - 1] + 1;
                } else dp[j] = 0; // 注意这里不相等的时候要有赋0的操作
                if (dp[j] > result) result = dp[j];
            }
        }
        return result;
    }
};

时间复杂度： $O (n \times m)$ ，n 为A长度，m为B长度
空间复杂度： $O (m)$

4 最长公共子序列

1143.最长公共子序列

给定两个字符串 text1 和 text2，返回这两个字符串的最长公共子序列的长度。

一个字符串的子序列是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。

例如，“ace” 是 “abcde” 的子序列，但 “aec” 不是 “abcde” 的子序列。两个字符串的「公共子序列」是这两个字符串所共同拥有的子序列。

若这两个字符串没有公共子序列，则返回 0。

示例 1:

输入：text1 = “abcde”, text2 = “ace”
输出：3
解释：最长公共子序列是 “ace”，它的长度为 3。

示例 2:
输入：text1 = “abc”, text2 = “abc”
输出：3
解释：最长公共子序列是 “abc”，它的长度为 3。

示例 3:
输入：text1 = “abc”, text2 = “def”
输出：0
解释：两个字符串没有公共子序列，返回 0。

提示:

1 <= text1.length <= 1000
1 <= text2.length <= 1000 输入的字符串只含有小写英文字符。

举个栗子分析就能发现dp状态转移方程

class Solution {
public:
    int longestCommonSubsequence(string text1, string text2) {
        int n = text1.size();
        int m = text2.size();
        vector<vector<int>> dp(n+1, vector<int>(m+1,0));
        int res = 0;
        for(int i = 1;  i <= n; ++i){
            for(int j = 1; j <= m; ++j){
                if(text1[i-1] == text2[j-1]){
                    dp[i][j] = dp[i-1][j-1] + 1;
                }else{
                    dp[i][j] = max(dp[i-1][j], dp[i][j-1]);
                }
                res = max(dp[i][j], res);
            }
        }
        return res;
    }
};

5 不相交的线

1035.不相交的线

我们在两条独立的水平线上按给定的顺序写下 A 和 B 中的整数。

现在，我们可以绘制一些连接两个数字 A[i] 和 B[j] 的直线，只要 A[i] == B[j]，且我们绘制的直线不与任何其他连线（非水平线）相交。

以这种方法绘制线条，并返回我们可以绘制的最大连线数。

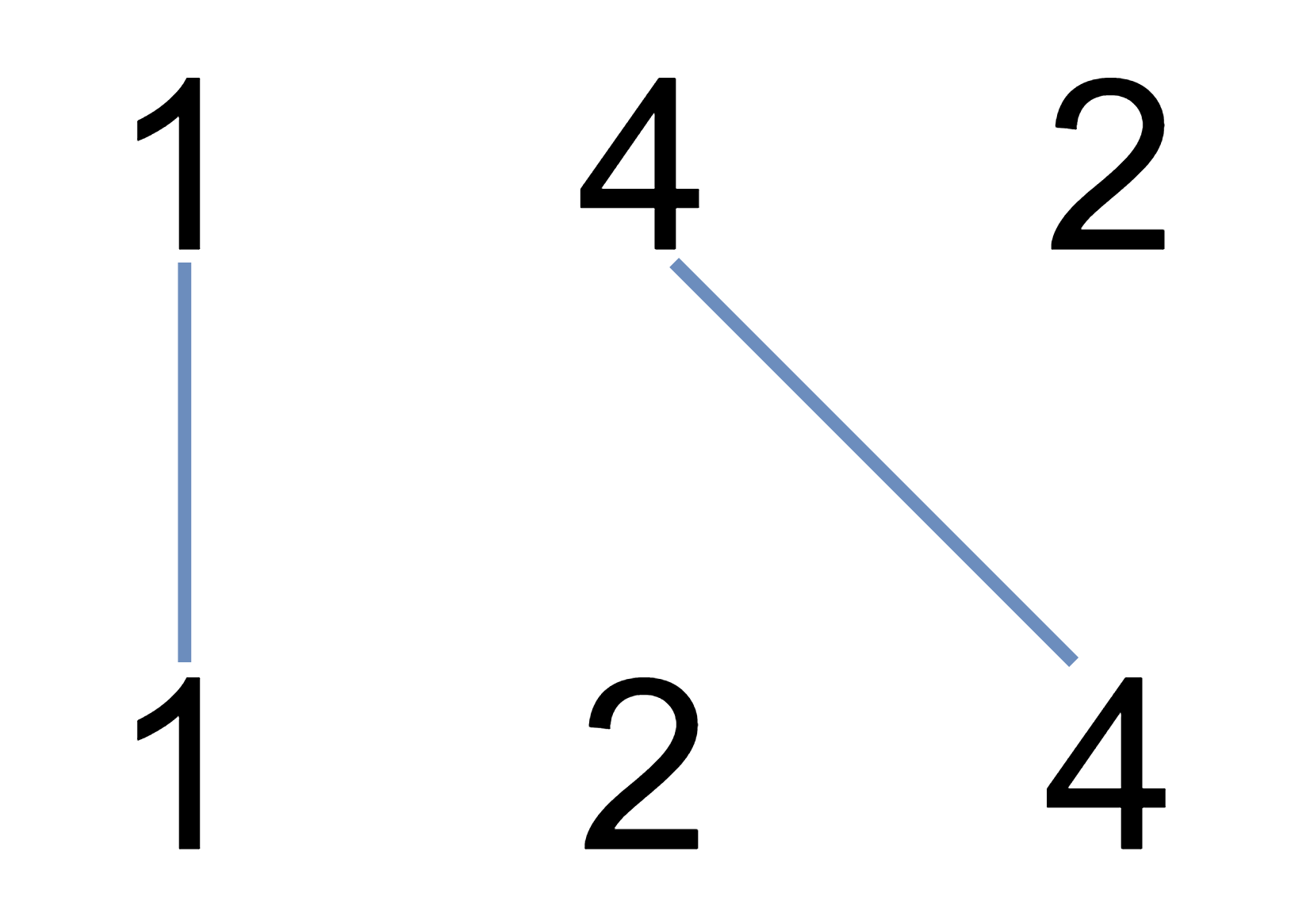
输入：nums1 = [1,4,2], nums2 = [1,2,4]
输出：2
解释：可以画出两条不交叉的线，如上图所示。
但无法画出第三条不相交的直线，因为从 nums1[1]=4 到 nums2[2]=4 的直线将与从 nums1[2]=2 到 nums2[1]=2 的直线相交。

这道题有两个关键的地方

不能改变顺序

不可相交

class Solution {
public:
    int maxUncrossedLines(vector<int>& nums1, vector<int>& nums2) {
        // 这道题其实就是最长公共子序列的变形
        //dp[i][j] 表示以i-1为结尾的nums1与j-1为结尾的nums2的最长公共字符串
        int n = nums1.size();
        int m = nums2.size();
        if(n==0 || m == 0) return 0;
        vector<vector<int>> dp(n+1, vector<int>(m+1,0));
        int res = 0;
        for(int i = 1; i <= n; ++i){
            for(int j = 1; j<=m; ++j){
                if(nums1[i-1] == nums2[j-1]){
                    dp[i][j] = dp[i-1][j-1] + 1;
                }else{
                    dp[i][j] = max(dp[i-1][j], dp[i][j-1]);
                }
                res = max(dp[i][j], res);
            }
        }
        return res;
    }
};

6 最大子数组和

最大子数组和

关键点在于定义dp

dp[i] 表示加入nums[i]后连续数组的最大和

            dp[i] = max(dp[i-1] + nums[i], nums[i]);
            maxSum = max(dp[i],maxSum);

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        // 动态规划
        int maxSum = INT_MIN;
        int n = nums.size();
        vector<int>dp(n);
        dp[0] = nums[0];
        maxSum = nums[0];      
        for(int i  = 1; i < nums.size(); i++){
            dp[i] = max(dp[i-1] + nums[i], nums[i]);
            maxSum = max(dp[i],maxSum);
        }
        return maxSum;
    }
};

7 判断子序列

392. 判断子序列

class Solution {
public:
    bool isSubsequence(string s, string t) {
        int n = s.size();
        int m = t.size();
        vector<vector<int>>dp(n+1, vector<int>(m+1,0));
        for(int i = 1; i <=n; ++i){
            for(int j = 1; j<=m; ++j){
                if(s[i-1] == t[j-1]){
                    // 相等的长度+1
                    // dp[i-1][j-1]
                    dp[i][j] = dp[i-1][j-1] + 1;
                }else{
                    // 如果不相等,需要删除
                    // 则看的是s[i-1]与t[j-2]的结果
                    // dp[j-1]
                    dp[i][j] = dp[i][j-1];
                }
            }
        }
        if(dp[n][m] == n) return true;
        else return false;
    }
};

8 编辑距离

72. 编辑距离

class Solution {
public:
    int minDistance(string word1, string word2) {
        // 动态规划
        // dp[i][j]表示i-1为结尾的word1字符串与j-1结尾的字符串的最小编辑距离
        int n = word1.size();
        int m = word2.size();
        vector<vector<int>> dp(n+1,vector<int>(m+1,0));
        // 初始化
        // dp[i][0]相当于i结尾的字符串与空字符串的编辑距离
        for(int i = 0; i <=n; ++i) dp[i][0] = i;
        for(int j = 0; j <=m; ++j) dp[0][j] = j;
        for(int i = 1; i <= n; ++i){
            for(int j = 1; j <= m; ++j){
                if(word1[i-1] == word2[j-1]){
                    dp[i][j] = dp[i-1][j-1];
                }else{
                    // 增 删 改
                    dp[i][j] = min({dp[i][j-1], dp[i-1][j], dp[i-1][j-1]}) + 1;
                }
            }
        }
        return dp[n][m];
    }
};

9 两个字符串的删除操作

583. 两个字符串的删除操作

class Solution {
public:
    int minDistance(string word1, string word2) {
        // dp[i][j] 以i-1的word1字符串与以j-1的word2字符串的相同的最小步数
        int n = word1.size();
        int m = word2.size();
        vector<vector<int>> dp(n+1, vector<int>(m+1));
        // 初始化
        for(int i = 0; i <= n; ++i) dp[i][0] = i;
        for(int j = 1; j<= m; ++j) dp[0][j] = j;
        // 分为相等和不相等两大类
        for(int i = 1; i<=n; ++i){
            for(int j = 1; j<=m; ++j){
                if(word1[i-1] == word2[j-1]){
                    dp[i][j] = dp[i-1][j-1];
                }else{
                    // 有三种情况
                    // word1 删除一个，word2删除一个  word1,word2删除
                    dp[i][j] = min({dp[i-1][j] + 1, dp[i][j-1] + 1, dp[i-1][j-1] + 2});
                }
            }
        }
        return dp[n][m];
    }
};

10 编辑距离问题小结：

判断子序列

动态规划：392.判断子序列 (opens new window)给定字符串 s 和 t ，判断 s 是否为 t 的子序列。

dp[i][j]表示以下标i-1为结尾的字符串s，和以下标j-1为结尾的字符串t，相同子序列的长度为dp[i][j]。

这道题目其实是可以用双指针或者贪心的的，但是我在开篇的时候就说了这是编辑距离的入门题目，因为从题意中我们也可以发现，只需要计算删除的情况，不用考虑增加和替换的情况。

if (s[i - 1] == t[j - 1])
- t中找到了一个字符在s中也出现了
if (s[i - 1] != t[j - 1])
- 相当于t要删除元素，继续匹配

状态转移方程：

if (s[i - 1] == t[j - 1]) dp[i][j] = dp[i - 1][j - 1] + 1;
else dp[i][j] = dp[i][j - 1];

不同的子序列

动态规划：115.不同的子序列 (opens new window)给定一个字符串 s 和一个字符串 t ，计算在 s 的子序列中 t 出现的个数。

本题虽然也只有删除操作，不用考虑替换增加之类的，但相对于动态规划：392.判断子序列 (opens new window)就有难度了，这道题目双指针法可就做不了。

当s[i - 1] 与 t[j - 1]相等时，dp[i][j]可以有两部分组成。

一部分是用s[i - 1]来匹配，那么个数为dp[i - 1][j - 1]。
一部分是不用s[i - 1]来匹配，个数为dp[i - 1][j]。

这里可能有同学不明白了，为什么还要考虑不用s[i - 1]来匹配，都相同了指定要匹配啊。

例如： s：bagg 和 t：bag ，s[3] 和 t[2]是相同的，但是字符串s也可以不用s[3]来匹配，即用s[0]s[1]s[2]组成的bag。

当然也可以用s[3]来匹配，即：s[0]s[1]s[3]组成的bag。

所以当s[i - 1] 与 t[j - 1]相等时，dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];

当s[i - 1] 与 t[j - 1]不相等时，dp[i][j]只有一部分组成，不用s[i - 1]来匹配，即：dp[i - 1][j]

所以递推公式为：dp[i][j] = dp[i - 1][j];

状态转移方程：

if (s[i - 1] == t[j - 1]) {
    dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
} else {
    dp[i][j] = dp[i - 1][j];
}

两个字符串的删除操作

动态规划：583.两个字符串的删除操作 (opens new window)给定两个单词 word1 和 word2，找到使得 word1 和 word2 相同所需的最小步数，每步可以删除任意一个字符串中的一个字符。

当word1[i - 1] 与 word2[j - 1]相同的时候
当word1[i - 1] 与 word2[j - 1]不相同的时候

当word1[i - 1] 与 word2[j - 1]相同的时候，dp[i][j] = dp[i - 1][j - 1];

当word1[i - 1] 与 word2[j - 1]不相同的时候，有三种情况：

情况一：删word1[i - 1]，最少操作次数为dp[i - 1][j] + 1

情况二：删word2[j - 1]，最少操作次数为dp[i][j - 1] + 1

情况三：同时删word1[i - 1]和word2[j - 1]，操作的最少次数为dp[i - 1][j - 1] + 2

那最后当然是取最小值，所以当word1[i - 1] 与 word2[j - 1]不相同的时候，递推公式：dp[i][j] = min({dp[i - 1][j - 1] + 2, dp[i - 1][j] + 1, dp[i][j - 1] + 1});

状态转移方程：

if (word1[i - 1] == word2[j - 1]) {
    dp[i][j] = dp[i - 1][j - 1];
} else {
    dp[i][j] = min({dp[i - 1][j - 1] + 2, dp[i - 1][j] + 1, dp[i][j - 1] + 1});
}

编辑距离

动态规划：72.编辑距离 (opens new window)给你两个单词 word1 和 word2，请你计算出将 word1 转换成 word2 所使用的最少操作数。

编辑距离终于来了，有了前面三道题目的铺垫，应该有思路了，本题是两个字符串可以增删改，比动态规划：判断子序列 (opens new window)，动态规划：不同的子序列 (opens new window)，动态规划：两个字符串的删除操作 (opens new window)都要复杂的多。

在确定递推公式的时候，首先要考虑清楚编辑的几种操作，整理如下：

if (word1[i - 1] == word2[j - 1])
- 不操作
if (word1[i - 1] != word2[j - 1])
- 增
- 删
- 换

也就是如上四种情况。

if (word1[i - 1] == word2[j - 1]) 那么说明不用任何编辑，dp[i][j] 就应该是 dp[i - 1][j - 1]，即dp[i][j] = dp[i - 1][j - 1];

此时可能有同学有点不明白，为啥要即dp[i][j] = dp[i - 1][j - 1]呢？

那么就在回顾上面讲过的dp[i][j]的定义，word1[i - 1] 与 word2[j - 1]相等了，那么就不用编辑了，以下标i-2为结尾的字符串word1和以下标j-2为结尾的字符串word2的最近编辑距离dp[i - 1][j - 1] 就是 dp[i][j]了。

在下面的讲解中，如果哪里看不懂，就回想一下dp[i][j]的定义，就明白了。

在整个动规的过程中，最为关键就是正确理解dp[i][j]的定义！

if (word1[i - 1] != word2[j - 1])，此时就需要编辑了，如何编辑呢？

操作一：word1增加一个元素，使其word1[i - 1]与word2[j - 1]相同，那么就是以下标i-2为结尾的word1 与 i-1为结尾的word2的最近编辑距离加上一个增加元素的操作。

即 dp[i][j] = dp[i - 1][j] + 1;

操作二：word2添加一个元素，使其word1[i - 1]与word2[j - 1]相同，那么就是以下标i-1为结尾的word1 与 j-2为结尾的word2的最近编辑距离加上一个增加元素的操作。

即 dp[i][j] = dp[i][j - 1] + 1;

这里有同学发现了，怎么都是添加元素，删除元素去哪了。

word2添加一个元素，相当于word1删除一个元素，例如 word1 = “ad” ，word2 = “a”，word2添加一个元素d，也就是相当于word1删除一个元素d，操作数是一样！

操作三：替换元素，word1替换word1[i - 1]，使其与word2[j - 1]相同，此时不用增加元素，那么以下标i-2为结尾的word1 与 j-2为结尾的word2的最近编辑距离加上一个替换元素的操作。

即 dp[i][j] = dp[i - 1][j - 1] + 1;

综上，当 if (word1[i - 1] != word2[j - 1]) 时取最小的，即：dp[i][j] = min({dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]}) + 1;

递归公式代码如下：

if (word1[i - 1] == word2[j - 1]) {
    dp[i][j] = dp[i - 1][j - 1];
}
else {
    dp[i][j] = min({dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]}) + 1;
}

11 回文子串

回文子串

给定一个字符串，你的任务是计算这个字符串中有多少个回文子串。

具有不同开始位置或结束位置的子串，即使是由相同的字符组成，也会被视作不同的子串。

示例 1：

输入：“abc” 输出：3 解释：三个回文子串: “a”, “b”, “c”

示例 2：

输入：“aaa” 输出：6 解释：6个回文子串: “a”, “a”, “a”, “aa”, “aa”, “aaa”

提示：

输入的字符串长度不会超过 1000

确定dp数组

布尔类型的dp[i][j]：表示区间范围[i,j] （注意是左闭右闭）的子串是否是回文子串，如果是dp[i][j]为true，否则为false。

确定地推公式

在确定地推公式时，就要分析如下几种情况。

当s[i]与s[j]不相等，那没啥好说的了，dp[i][j]一定是false。
当s[i]与s[j]相等时，这就复杂一些了，有如下三种情况

情况一：下标i 与 j相同，同一个字符例如a，当然是回文子串
情况二：下标i 与 j相差为1，例如aa，也是回文子串
情况三：下标：i 与 j相差大于1的时候，例如cabac
- 此时s[i]与s[j]已经相同了，我们看i到j区间是不是回文子串就看aba是不是回文就可以了，那么aba的区间就是 i+1 与 j-1区间
- 这个区间是不是回文就看dp[i + 1][j - 1]是否为true。

if (s[i] == s[j]) {
    if (j - i <= 1) { // 情况一 和 情况二
        result++;
        dp[i][j] = true;
    } else if (dp[i + 1][j - 1]) { // 情况三
        result++;
        dp[i][j] = true;
    }
}

数组初始化

初始化的时候全部为false

遍历顺序

从递推方程可以看出，由于dp[i+1][j-1]在dp[i][j]下方，未初始化就使用了

因此需要从下到上从左到右遍历

	`dp[i][j]`
`dp[i-1][j+1]`

举例推导

输入：“aaa”

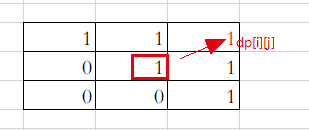
图中有6个true，所以就是有6个回文子串。

注意因为dp[i][j]的定义，所以j一定是大于等于i的，那么在填充dp[i][j]的时候一定是只填充右上半部分。

class Solution {
public:
    int countSubstrings(string s) {
        vector<vector<bool>> dp(s.size(), vector<bool>(s.size(), false));
        int result = 0;
        for (int i = s.size() - 1; i >= 0; i--) {  // 注意遍历顺序
            for (int j = i; j < s.size(); j++) {
                if (s[i] == s[j]) {
                    if (j - i <= 1) { // 情况一 和 情况二
                        result++;
                        dp[i][j] = true;
                    } else if (dp[i + 1][j - 1]) { // 情况三
                        result++;
                        dp[i][j] = true;
                    }
                }
            }
        }
        return result;
    }
};

12 最长回文子串

给你一个字符串 s，找到 s 中最长的回文子串。

最长回文子串

示例 1：

输入：s = “babad”
输出：“bab”
解释：“aba” 同样是符合题意的答案。
示例 2：

输入：s = “cbbd”
输出：“bb”

最大的区别在于：

这里只需要统计最长的回文串，而不是统计回文串

所以只需修改的：

添加最大的连续长度的判断

                if(dp[i][j] && j - i + 1 >= maxLen){
                        maxLen = j - i + 1;
                        start = i;
                        end = j;
                }

class Solution {
public:
    string longestPalindrome(string s) {
        vector<vector<bool>> dp(s.size(), vector<bool>(s.size(), false));
        if(s.size() <= 1 ) return s;
        int result = 0;
        int maxLen = 0;
        int start = 0;
        int end = 0;
        for (int i = s.size() - 1; i >= 0; i--) {  // 注意遍历顺序
            for (int j = i; j < s.size(); j++) {
                if (s[i] == s[j]) {
                    if (j - i <= 1) { // 情况一 和 情况二
                        dp[i][j] = true;
                    } else if (dp[i + 1][j - 1]) { // 情况三
                        result++;
                        dp[i][j] = true;
                    }
                }
                if(dp[i][j] && j - i + 1 >= maxLen){
                        maxLen = j - i + 1;
                        start = i;
                        end = j;
                }
            }
        }
        return s.substr(start,end - start + 1);
    }
};

13 最长回文子序列

确定dp数组（dp table）以及下标的含义

dp[i][j]：字符串s在[i, j]范围内最长的回文子序列的长度为dp[i][j]。

确定递推公式

如果s[i]与s[j]相同，那么dp[i][j] = dp[i + 1][j - 1] + 2;

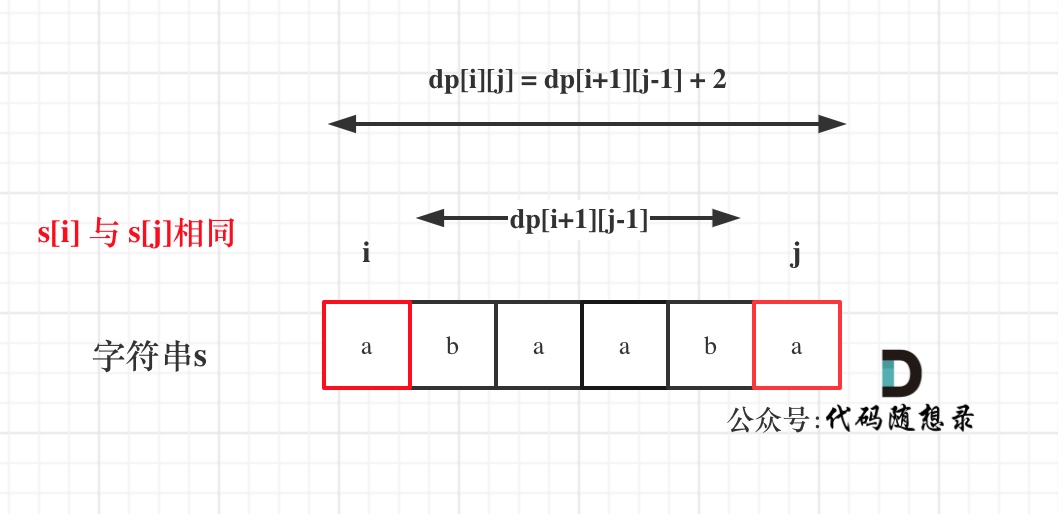
516.最长回文子序列

如果不相等则取两端部分的最大值分别加入s[i]、s[j]看看哪一个可以组成最长的回文子序列。

dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);

初始化

根据定义 i -> i为1， 初始化为0

遍历顺序

和之前一样，防止dp[i+1][j-1]被覆盖，同时要考虑dp[i+1][j]

需要注意的是由于dp[i+1][j] 所以j+1开始遍历

class Solution {
public:
    int longestPalindromeSubseq(string s) {
        int n = s.size();
        if(n <= 1){
            return n;
        }
        // dp[i][j] 表示[i][j]的最长回文子序列的长度
        vector<vector<int>> dp(n+1, vector<int>(n+1,0));
        for(int i = 0; i <=n; i++){
            dp[i][i] = 1;
        }
        for(int i = n-1; i >= 0; --i){
            for(int j = i + 1; j <n; ++j){
                if(s[i] == s[j]){
                    dp[i][j] = dp[i+1][j-1] + 2;
                }else{
                    dp[i][j] = max(dp[i+1][j], dp[i][j-1]);
                }
            }
        }
        return dp[0][n-1];
    }
};

二、小结

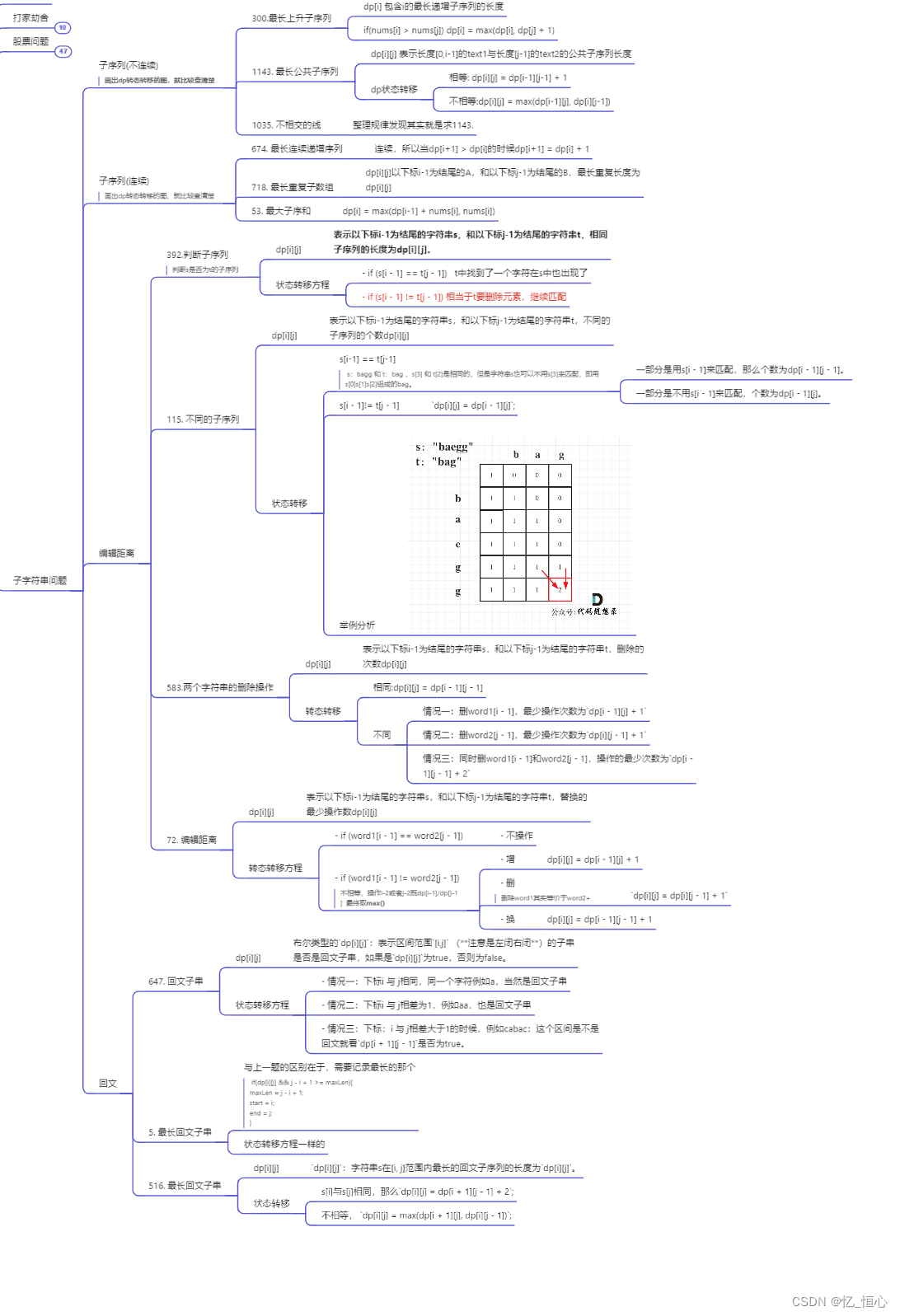
在这里插入图片描述

猜你喜欢

基于GPS 飞机导航的时间序列模型（Matlab代码实现）
MySQL · TokuDB · Savepoint漫谈
Centos7安装kvm服务器
【Android Gradle 插件】自定义 Gradle 插件优化图片 ② ( 压缩 png、jpg 图片 | 使用 pngcrush 压缩工具压缩 png 图片 )
platform device和platform driver简述
手把手玩转win8开发系列课程（9）
基于Hadoop开发网络云盘系统架构设计方案第一稿
InfluxDB基本概念和操作
卡巴斯基和微软的恶意软件分类——卡巴的更优雅些
IOS之UITableView——怎样刷新父页面的Cell
Demo of Python "Map Reduce Filter"
轻松自动化---selenium-webdriver(python) (六)
中职网络安全攻防之SSH服务加固方法
[翻译] JFMinimalNotifications
js实现搜索数组中元素插入的位置

相关主题

LeetCode--N-Queens
leetcode 654 最大二叉树
leetcode动态规划
LeetCode题解
Leetcode 78. 子集
[LeetCode]N-Queens
[LeetCode]Anagrams

zl程序教程

当前栏目

LeetCode动态规划基础题-子字符串问题(13题)

前言

一、子字符串问题

1 最长递增子序列

2 最长连续递增序列

3 最长重复子数组

4 最长公共子序列

5 不相交的线

6 最大子数组和

7 判断子序列

8 编辑距离

9 两个字符串的删除操作

10 编辑距离问题小结：

判断子序列

不同的子序列

两个字符串的删除操作

编辑距离

11 回文子串

12 最长回文子串

13 最长回文子序列

二、小结

相关文章