提供了编程的基础技术教程

zl程序教程

您现在的位置是：首页 >  后端

当前栏目

从baselines库的common/vec_env/vec_normalize.py模块看方差的近似计算方法

方法模块 py Common ENV 方差
2023-09-11 14:19:19 时间

在baselines库的common/vec_env/vec_normalize.py中计算方差的调用方法为：

RunningMeanStd

同时该计算函数的解释也一并给出了：

 

https://en.wikipedia.org/wiki/Algorithms_for_calculating_variance#Parallel_algorithm

 

 

 

也就是说这个函数是在对方差进行近似计算，找了下中文的这方面的资料：

上图来自：https://baijiahao.baidu.com/s?id=1715371851391883847&wfr=spider&for=pc

 

 

可以看到在wiki上给出了python的计算代码：

def shifted_data_variance(data):
    if len(data) < 2:
        return 0.0
    K = data[0]
    n = Ex = Ex2 = 0.0
    for x in data:
        n = n + 1
        Ex += x - K
        Ex2 += (x - K) * (x - K)
    variance = (Ex2 - (Ex * Ex) / n) / (n - 1)
    # use n instead of (n-1) if want to compute the exact variance of the given data
    # use (n-1) if data are samples of a larger population
    return variance
View Code

该代码的计算公式为：

 

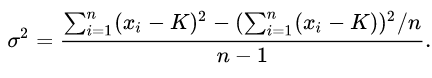
也就是说在样本数据较大的情况下可以使用该计算方法来近似计算样本方差。

 

给出自己的测试代码：

import numpy as np

data = np.random.normal(10, 5, 100000000)


print(data)
print(data.shape)
print(np.mean(data), np.var(data))

print('......')
def shifted_data_variance(data, K):
    if len(data) < 2:
        return 0.0
    # K = data[0]
    n = Ex = Ex2 = 0.0
    for x in data:
        n = n + 1
        Ex += x - K
        Ex2 += (x - K) * (x - K)
    variance = (Ex2 - (Ex * Ex) / n) / (n - 1)
    # use n instead of (n-1) if want to compute the exact variance of the given data
    # use (n-1) if data are samples of a larger population
    return variance

print(shifted_data_variance(data, data[0]))
print(shifted_data_variance(data, 0))
print(shifted_data_variance(data, -10000))

运行结果：

 

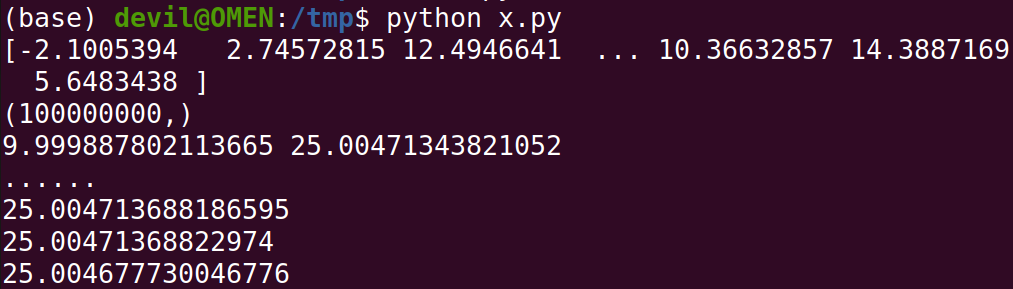
可以知道如果K值越接近真实的均值那么所得到的近似方差会更加逼近真实的样本方差。

 

那么如果样本数据较少的情况呢，上面的测试使用的是100000000个数据样本，如果是100个呢，给出测试：

代码：

import numpy as np

data = np.random.normal(10, 5, 100)


print(data)
print(data.shape)
print(np.mean(data), np.var(data))

print('......')
def shifted_data_variance(data, K):
    if len(data) < 2:
        return 0.0
    # K = data[0]
    n = Ex = Ex2 = 0.0
    for x in data:
        n = n + 1
        Ex += x - K
        Ex2 += (x - K) * (x - K)
    variance = (Ex2 - (Ex * Ex) / n) / (n - 1)
    # use n instead of (n-1) if want to compute the exact variance of the given data
    # use (n-1) if data are samples of a larger population
    return variance

print(shifted_data_variance(data, data[0]))
print(shifted_data_variance(data, 0))
print(shifted_data_variance(data, -10000))
View Code

运行结果：

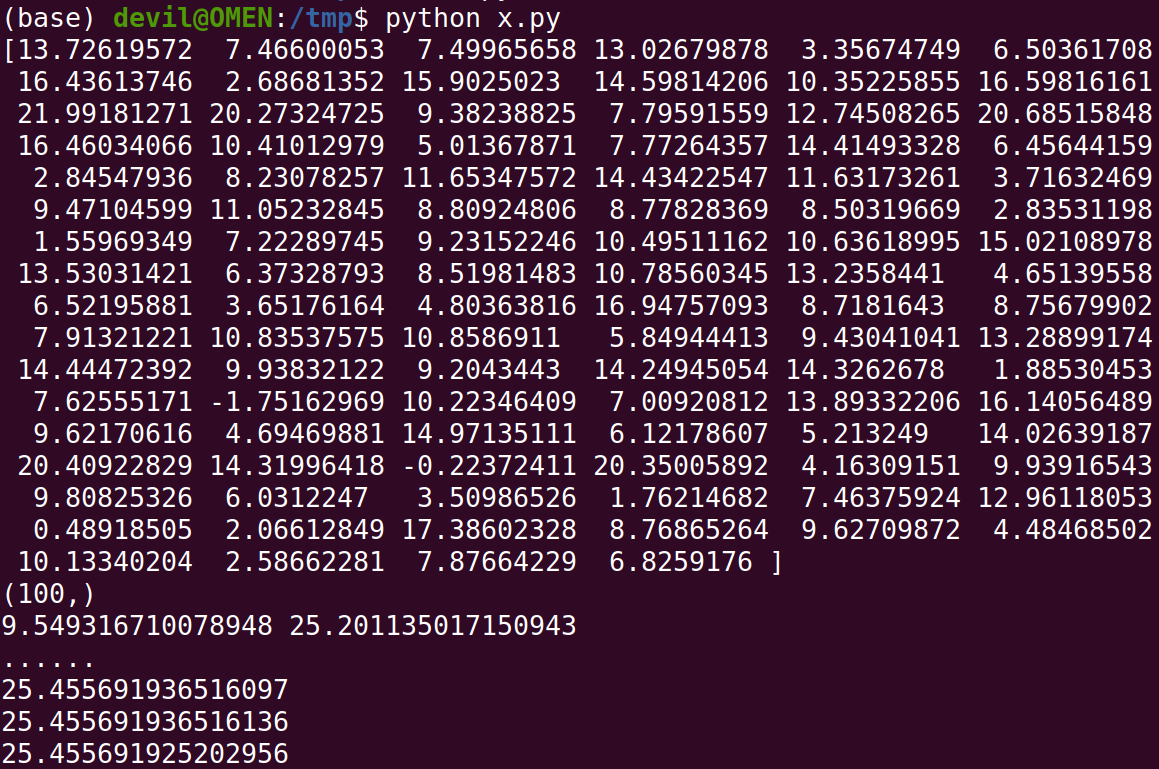
可以看到和数据样本较大规模的情况一样，该方法依然可以得到非常好的近似方差，同时K值越接近真实均值近似方差就越接近真实方差，不过这里可以看到这里的差别也是在小数点后九位，因此这个差距可以看做没有。

 

 

总结：

这个计算方差的最大好处就是可以在不计算样本均值的情况下就直接计算样本方差，该种计算方法非常适合样本数据量在不断增加的情况，不过这里的样本数据量增加也是在服从同一分布的条件下的。

比如我们需要不断的从一个数据分布中获得样本并获得分布的方差，如果不适用这种近似计算方差的方法每当我们得到一个新的样本都需要重新计算样本的方差，这样就会成几何倍数的增加计算量，毕竟标准的方差计算是需要遍历所有样本数据的。

给出标准的方差计算公式：

 

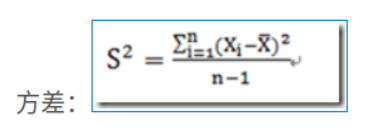
图片源自：https://www.cnblogs.com/devilmaycry812839668/p/16072130.html

 

不得不说算法设计可以有效提升计算性能。

 

 

================================================

 

不过根据wiki的说明可以知道，上述的方法在计算过程中设计到大量的求和sum计算，而求和计算由于会由于浮点数计算时的精度取舍从而影响最终的结果精度：

This algorithm is numerically stable if n is small.[1][4] However, the results of both of these simple algorithms ("naïve" and "two-pass") can depend inordinately on the ordering of the data and can give poor results for very large data sets due to repeated roundoff error in the accumulation of the sums. Techniques such as compensated summation can be used to combat this error to a degree.

 

================================================

 

 

 

 

在baselines库中使用的求方差的方法为：

也就是baselines中的函数：

class RunningMeanStd(object):
    # https://en.wikipedia.org/wiki/Algorithms_for_calculating_variance#Parallel_algorithm
    def __init__(self, epsilon=1e-4, shape=()):
        self.mean = np.zeros(shape, 'float64')
        self.var = np.ones(shape, 'float64')
        self.count = epsilon

    def update(self, x):
        batch_mean = np.mean(x, axis=0)
        batch_var = np.var(x, axis=0)
        batch_count = x.shape[0]
        self.update_from_moments(batch_mean, batch_var, batch_count)

    def update_from_moments(self, batch_mean, batch_var, batch_count):
        self.mean, self.var, self.count = update_mean_var_count_from_moments(
            self.mean, self.var, self.count, batch_mean, batch_var, batch_count)

def update_mean_var_count_from_moments(mean, var, count, batch_mean, batch_var, batch_count):
    delta = batch_mean - mean
    tot_count = count + batch_count

    new_mean = mean + delta * batch_count / tot_count
    m_a = var * count
    m_b = batch_var * batch_count
    M2 = m_a + m_b + np.square(delta) * count * batch_count / tot_count
    new_var = M2 / tot_count
    new_count = tot_count

    return new_mean, new_var, new_count

使用自己的测试代码：

import numpy as np

data = np.random.normal(10, 5, 1000000)


print(data)
print(data.shape)
print(np.mean(data), np.var(data))

print('......')
def shifted_data_variance(data, K):
    if len(data) < 2:
        return 0.0
    # K = data[0]
    n = Ex = Ex2 = 0.0
    for x in data:
        n = n + 1
        Ex += x - K
        Ex2 += (x - K) * (x - K)
    variance = (Ex2 - (Ex * Ex) / n) / (n - 1)
    # use n instead of (n-1) if want to compute the exact variance of the given data
    # use (n-1) if data are samples of a larger population
    return variance

print(shifted_data_variance(data, data[0]))
print(shifted_data_variance(data, 0))
print(shifted_data_variance(data, -10000))

print('......')

class RunningMeanStd(object):
    # https://en.wikipedia.org/wiki/Algorithms_for_calculating_variance#Parallel_algorithm
    def __init__(self, epsilon=1e-4, shape=()):
        self.mean = np.zeros(shape, 'float64')
        self.var = np.ones(shape, 'float64')
        self.count = epsilon

    def update(self, x):
        batch_mean = np.mean(x, axis=0)
        batch_var = np.var(x, axis=0)
        batch_count = x.shape[0]
        self.update_from_moments(batch_mean, batch_var, batch_count)

    def update_from_moments(self, batch_mean, batch_var, batch_count):
        self.mean, self.var, self.count = update_mean_var_count_from_moments(
            self.mean, self.var, self.count, batch_mean, batch_var, batch_count)

def update_mean_var_count_from_moments(mean, var, count, batch_mean, batch_var, batch_count):
    delta = batch_mean - mean
    tot_count = count + batch_count

    new_mean = mean + delta * batch_count / tot_count
    m_a = var * count
    m_b = batch_var * batch_count
    M2 = m_a + m_b + np.square(delta) * count * batch_count / tot_count
    new_var = M2 / tot_count
    new_count = tot_count

    return new_mean, new_var, new_count

rsd = RunningMeanStd(0)
for d in range(10000):
    rsd.update(data[d*100:(d+1)*100])
print(rsd.mean, rsd.var, rsd.count)

运行结果：

 

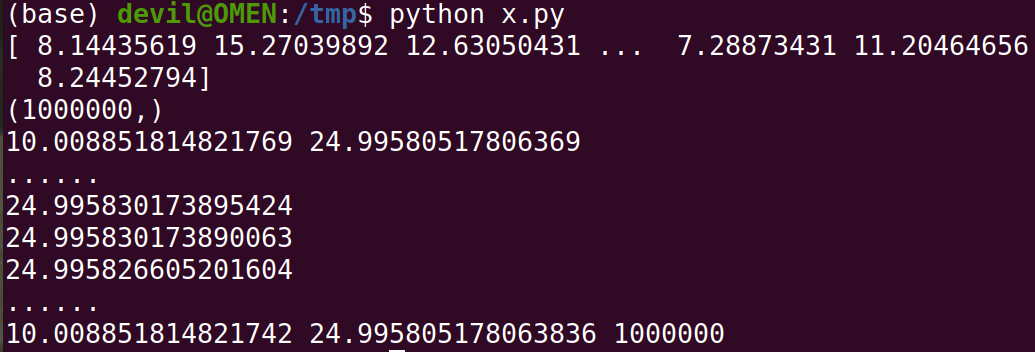
从运行结果中可以看到这种的求方差方法也可以得到很好的效果。

 

 

上面的这个baselines库中的求解方差的方法主要是适用于增量数据以集合的形式出现，在机器学习中可以看做是不断有的额batch的数据来到。

比如说我们收到的数据是一个集合增量，通过融合已有集合数据的方差、均值以及新到集合的方差、均值就可以得到合集的方差。

 

 

=======================================================

 

 

本文中的求解增量数据的方差的的方法来源：

https://en.wikipedia.org/wiki/Algorithms_for_calculating_variance#Parallel_algorithm

 

由于这里的增强数据方差求解方法比较难以证明，因此这里也是直接拿过来进行使用。

 

 

 

========================

 

相关文章