机器学习笔记之条件随机场(五)推断任务介绍
机器学习笔记之条件随机场——推断任务介绍
引言
上一节介绍了条件随机场的建模对象——条件概率 P ( I ∣ O ) \mathcal P(\mathcal I \mid \mathcal O) P(I∣O)参数形式和向量形式的表示。本节将介绍条件随机场面对的任务,并针对推断任务进行介绍。
回顾:条件随机场
条件随机场(Condition Random Field,CRF)是一种结合了最大熵模型(Maximum Entropy Model)和隐马尔可夫模型(Hidden Markov Model,HMM)特点的无向图模型。其概率图结构表示如下:
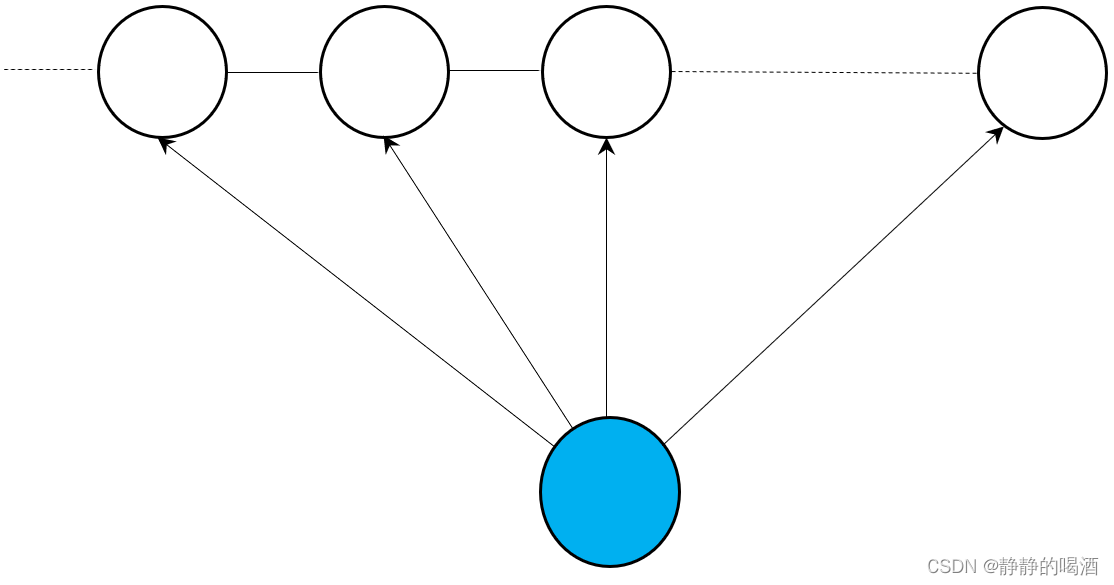
并且,它是一个概率判别模型,它的建模对象是关于隐变量的条件概率
P
(
I
∣
O
)
\mathcal P(\mathcal I \mid \mathcal O)
P(I∣O):
P
(
I
∣
O
)
=
1
Z
exp
[
∑
t
=
1
T
−
1
∑
m
=
1
M
λ
m
⋅
s
m
(
i
t
+
1
,
i
t
,
O
)
+
∑
t
=
1
T
∑
l
=
1
L
η
l
⋅
g
l
(
i
t
,
O
)
]
=
1
Z
(
O
,
θ
)
exp
⟨
θ
,
H
(
i
t
+
1
,
i
t
,
O
)
⟩
{
θ
=
(
λ
1
,
⋯
,
λ
M
,
η
1
,
⋯
,
η
L
)
T
H
(
i
t
+
1
,
i
t
,
O
)
=
(
∑
t
=
1
T
−
1
s
(
i
t
+
1
,
i
t
,
O
)
∑
t
−
1
T
g
(
i
t
,
O
)
)
\begin{aligned} \mathcal P(\mathcal I \mid \mathcal O) & = \frac{1}{\mathcal Z} \exp \left[\sum_{t=1}^{T-1} \sum_{m=1}^{\mathcal M} \lambda_m \cdot s_m(i_{t+1},i_t,\mathcal O) + \sum_{t=1}^{T} \sum_{l=1}^{\mathcal L} \eta_l \cdot g_l(i_t,\mathcal O)\right] \\ & = \frac{1}{\mathcal Z(\mathcal O,\theta)} \exp \left\langle \theta,\mathcal H(i_{t+1},i_t,\mathcal O)\right\rangle \quad \begin{cases} \theta = (\lambda_1,\cdots,\lambda_{\mathcal M},\eta_1,\cdots,\eta_{\mathcal L})^{T} \\ \mathcal H(i_{t+1},i_t,\mathcal O) = \begin{pmatrix} \sum_{t=1}^{T-1}s(i_{t+1},i_t,\mathcal O) \\ \quad \\ \sum_{t-1}^{T}g(i_t,\mathcal O) \end{pmatrix} \end{cases} \end{aligned}
P(I∣O)=Z1exp[t=1∑T−1m=1∑Mλm⋅sm(it+1,it,O)+t=1∑Tl=1∑Lηl⋅gl(it,O)]=Z(O,θ)1exp⟨θ,H(it+1,it,O)⟩⎩⎪⎪⎪⎨⎪⎪⎪⎧θ=(λ1,⋯,λM,η1,⋯,ηL)TH(it+1,it,O)=⎝⎛∑t=1T−1s(it+1,it,O)∑t−1Tg(it,O)⎠⎞
并且,条件随机场打破了齐次马尔可夫假设和观测独立性假设,虽然没有脱离动态模型的范畴,但针对的目标是时间/序列状态转移过程有限的情况。例如:一条文本句子,一条蛋白质序列。
其中 s m ( i t + 1 , i t , O ) s_m(i_{t+1},i_t,\mathcal O) sm(it+1,it,O)被称作转移特征函数(Transition Feature Function), g l ( i t , O ) g_l(i_t,\mathcal O) gl(it,O)被称作状态特征函数(State Feature Function)。以词性标注的角度为例,描述这两个特征函数。
-
一个句子由词语组成,这些词语的词性在句子中存在关联关系。例如: The boy knocked at the watermelon \text{The boy knocked at the watermelon} The boy knocked at the watermelon(男孩敲了敲西瓜)。
-
我们需要定义合适的特征函数,来刻画数据的一些可能成立或者期望成立的经验特性。
当 t = 3 t=3 t=3时,此时的观测变量 o 3 o_3 o3为 knocked \text{knocked} knocked,而下一时刻的词语是介词 at \text{at} at。在条件随机场——背景介绍中提到特征函数通常是实值函数,因此当前时刻的状态特征函数 g l ( i 3 , O ) g_l(i_3,\mathcal O) gl(i3,O)表示如下:
这里忽略‘时态’的影响,并且[ V \mathcal V V]表示动词;[ P \mathcal P P]表示介词。
g l ( i 3 , O ) = { 1 if i 3 = [ V ] and o 3 = ′ knock ′ 0 otherwise g_l(i_3,\mathcal O) = \begin{cases} 1 \quad \text{if } i_3 = [\mathcal V] \text{ and } o_3 = '\text{knock}' \\ 0 \quad \text{otherwise} \end{cases} gl(i3,O)={1if i3=[V] and o3=′knock′0otherwise
很明显, i 3 = [ V ] and o 3 = ′ knock ′ i_3 = [\mathcal V] \text{ and } o_3 = '\text{knock}' i3=[V] and o3=′knock′描述了一种既定事实,只要满足该事实条件, g l ( i 3 , O ) g_l(i_3,\mathcal O) gl(i3,O)才有它的存在价值。同理,关于两个隐变量共同作用的转移特征函数 s m ( i 4 , i 3 , O ) s_m(i_4,i_3,\mathcal O) sm(i4,i3,O)表示如下:
和状态特征函数类似,当“当前词语的词性是动词”且“下一个词语的词性是介词”,并且当前单词是knock \text{knock} knock时,该特征函数被启用。对应产生价值的大小由对应特征函数的参数λ m , η l \lambda_m,\eta_l λm,ηl决定。
s m ( i 4 , i 3 , O ) = { 1 if i 4 = [ P ] , i 3 = [ V ] and o 3 = ′ knock ′ 0 otherwise s_m(i_4,i_3,\mathcal O)= \begin{cases} 1 \quad \text{if } i_4 = [\mathcal P],i_3 = [\mathcal V] \text{ and } o_3 = '\text{knock}'\\ 0 \quad \text{otherwise}\end{cases} sm(i4,i3,O)={1if i4=[P],i3=[V] and o3=′knock′0otherwise
条件随机场要解决的任务
条件随机场作为一个概率图模型,其主要任务主要分为两个部分:
-
学习任务(Learning),主要针对模型参数进行求解。(Parameter Estimation)
对于条件随机场的学习任务,可以将其理解为:给定训练数据集 D \mathcal D D:样本/标签维度均是T T T,即样本维度和条件随机场建模的‘序列/时间长度相同’。不要和‘转置符号’弄混;从真实样本的角度观察,样本x ( i ) x^{(i)} x(i)可能是某一个句子,一个序列,而不是一个单词,一个氨基酸;对应的标签y ( i ) y^{(i)} y(i)可能是‘每个单词的词性标注组成的序列’。各样本之间属于‘独立同分布’,各样本之间不存在关联关系。
D = { ( x ( i ) , y ( i ) ) } i = 1 N x ( i ) , y ( i ) ∈ R T x ( i ) = ( x 1 ( i ) , x 2 ( i ) , ⋯ , x T ( i ) ) T → x 1 : T ( i ) y ( i ) = ( y 1 ( i ) , y 2 ( i ) , ⋯ , y T ( i ) ) T \begin{aligned} \mathcal D & = \{(x^{(i)},y^{(i)})\}_{i=1}^{N} \quad x^{(i)},y^{(i)} \in \mathbb R^T \\ x^{(i)} & = \left(x_1^{(i)},x_2^{(i)},\cdots,x_T^{(i)}\right)^T \to x_{1:T}^{(i)}\\ y^{(i)} & = \left(y_1^{(i)},y_2^{(i)},\cdots,y_T^{(i)}\right)^T \end{aligned} Dx(i)y(i)={(x(i),y(i))}i=1Nx(i),y(i)∈RT=(x1(i),x2(i),⋯,xT(i))T→x1:T(i)=(y1(i),y2(i),⋯,yT(i))T
对应图像示例如下:
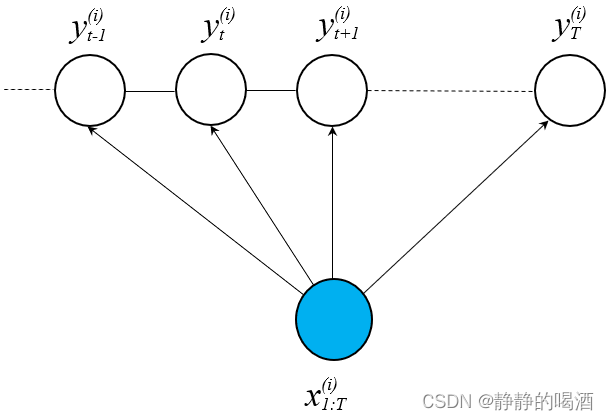
对于最优参数 θ ^ \hat {\theta} θ^的估计表示如下:
其朴素思想在于:希望预测的标签序列y y y能够与对应的样本x x x最大程度的匹配,即P ( y ∣ x ) \mathcal P(y \mid x) P(y∣x)越大越好。并且各样本之间独立同分布,因此在学习过程中,模型参数的评价标准就是对‘数据集合内’的所有样本的P ( y ∣ x ) \mathcal P(y \mid x) P(y∣x)都达到最大。
θ ^ = arg max θ ∏ i = 1 N P ( y ( i ) ∣ x ( i ) ) \begin{aligned} \hat {\theta} = \mathop{\arg\max}\limits_{\theta} \prod_{i=1}^N \mathcal P \left(y^{(i)} \mid x^{(i)}\right) \end{aligned} θ^=θargmaxi=1∏NP(y(i)∣x(i)) -
对于未知变量的推断任务(Inference):
在概率图模型——推断基本介绍中提到过关于推断的描述。- 通过联合概率分布,对边缘概率分布进行求解 (Marginal Probability):
P ( i t ∣ O ) = ∑ i 1 , ⋯ , i t − 1 , i t + 1 , ⋯ , i T P ( I ∣ O ) \mathcal P(i_t \mid \mathcal O) = \sum_{i_1,\cdots,i_{t-1},i_{t+1},\cdots,i_T}\mathcal P(\mathcal I \mid \mathcal O) P(it∣O)=i1,⋯,it−1,it+1,⋯,iT∑P(I∣O)
从样本角度观察,可以看作:给定一条完整句子序列的条件下,对句中某一单词词性的条件概率进行求解:
P ( y t ( i ) ∣ x 1 : T ( i ) ) \mathcal P(y_t^{(i)} \mid x_{1:T}^{(i)}) P(yt(i)∣x1:T(i)) - 求解条件概率分布(Conditional Probability):
I = I A ∪ I B → P ( I A ∣ I B ) \mathcal I = \mathcal I_{\mathcal A} \cup \mathcal I_{\mathcal B} \to \mathcal P(\mathcal I_{\mathcal A} \mid \mathcal I_{\mathcal B}) I=IA∪IB→P(IA∣IB)
由于条件随机场是概率判别模型,求解条件概率主要针对概率生成模型,对于概率判别模型基本没有意义。例如隐马尔可夫模型中的预测任务(Prediction):
齐次马尔可夫假设~
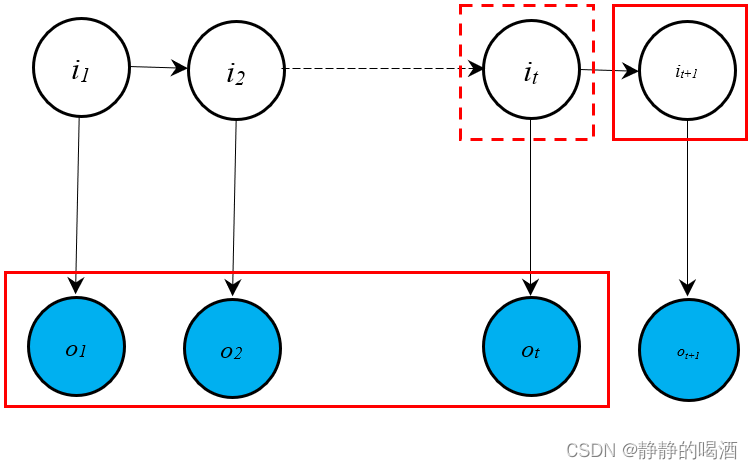
P ( i t + 1 ∣ o 1 , ⋯ , o t ) = ∑ i t P ( i t + 1 , i t ∣ o 1 , ⋯ , o t ) = ∑ i t P ( i t + 1 ∣ i t , o 1 , ⋯ , o t ) ⋅ P ( i t ∣ o 1 , ⋯ , o t ) = ∑ i t P ( i t + 1 ∣ i t ) ⋅ P ( i t ∣ o 1 , ⋯ , o t ) \begin{aligned} \mathcal P(i_{t+1} \mid o_1,\cdots,o_t) & = \sum_{i_t} \mathcal P(i_{t+1},i_t \mid o_1,\cdots,o_t) \\ & = \sum_{i_t} \mathcal P(i_{t+1} \mid i_t,o_1,\cdots,o_t) \cdot \mathcal P(i_{t} \mid o_1,\cdots,o_t) \\ & = \sum_{i_t} \mathcal P(i_{t+1} \mid i_t) \cdot \mathcal P(i_t \mid o_1,\cdots,o_t) \end{aligned} P(it+1∣o1,⋯,ot)=it∑P(it+1,it∣o1,⋯,ot)=it∑P(it+1∣it,o1,⋯,ot)⋅P(it∣o1,⋯,ot)=it∑P(it+1∣it)⋅P(it∣o1,⋯,ot)
此时,将预测任务转化为滤波任务(Filtering)。对应概率图描述表示如下:
- 最大后验概率推断(MAP Inference):主要针对解码任务(Decoding),依然以隐马尔可夫模型的解码任务为例,在求解
P
(
I
∣
O
)
=
P
(
i
1
,
⋯
,
i
T
∣
o
1
,
⋯
,
o
T
)
\mathcal P(\mathcal I\mid \mathcal O) = \mathcal P(i_1,\cdots,i_T \mid o_1,\cdots,o_T)
P(I∣O)=P(i1,⋯,iT∣o1,⋯,oT)过程中,需要求解一组适合的状态序列
I
^
\hat {\mathcal I}
I^,使得后验概率
P
(
I
^
∣
O
,
λ
)
\mathcal P(\hat {\mathcal I} \mid \mathcal O,\lambda)
P(I^∣O,λ)最大:
I ^ = arg max I P ( I ^ ∣ O , λ ) \hat {\mathcal I} = \mathop{\arg\max}\limits_{\mathcal I} \mathcal P(\hat{\mathcal I} \mid \mathcal O,\lambda) I^=IargmaxP(I^∣O,λ)
但实际求解过程并没有直接对 P ( I ∣ O ) \mathcal P(\mathcal I \mid \mathcal O) P(I∣O)进行求解,而是通过 维特比算法 求解 相邻时刻下,状态变量取值的联合概率分布之间的关系:
δ t ( k ) = max I t − 1 P ( O , I t − 1 , i t = q k ∣ λ ) δ t + 1 ( j ) = max I t P ( O , I t , i t + 1 = q j ∣ λ ) δ t ( k ) ⇔ ? δ t + 1 ( j ) \begin{aligned} \delta_t(k) & = \mathop{\max}\limits_{\mathcal I_{t-1}} \mathcal P(\mathcal O,\mathcal I_{t-1},i_t = q_k \mid \lambda) \\ \delta_{t+1}(j) & = \mathop{\max}\limits_{\mathcal I_t}\mathcal P(\mathcal O,\mathcal I_t,i_{t+1} = q_j \mid \lambda) \\ \delta_t(k) & \overset{\text{?}}{\Leftrightarrow}\delta_{t+1}(j) \end{aligned} δt(k)δt+1(j)δt(k)=It−1maxP(O,It−1,it=qk∣λ)=ItmaxP(O,It,it+1=qj∣λ)⇔?δt+1(j)
这种将 P ( I ∣ O , λ ) \mathcal P(\mathcal I \mid \mathcal O,\lambda) P(I∣O,λ)的问题转化为 P ( I , O ∣ λ ) \mathcal P(\mathcal I,\mathcal O \mid \lambda) P(I,O∣λ)的问题,用到了最大后验概率(Maximum a posteriori Probability,MAP)的思想:
I ^ = arg max I P ( I ∣ O , λ ) = arg max I P ( I , O ∣ λ ) P ( O , λ ) ∝ arg max I P ( I , O ∣ λ ) \begin{aligned} \hat {\mathcal I} & = \mathop{\arg\max}\limits_{\mathcal I} \mathcal P(\mathcal I \mid \mathcal O,\lambda) \\ & = \mathop{\arg\max}\limits_{\mathcal I} \frac{\mathcal P(\mathcal I,\mathcal O \mid \lambda)}{\mathcal P(\mathcal O,\lambda)} \\ & \propto \mathop{\arg\max}\limits_{\mathcal I} \mathcal P(\mathcal I,\mathcal O\mid \lambda) \end{aligned} I^=IargmaxP(I∣O,λ)=IargmaxP(O,λ)P(I,O∣λ)∝IargmaxP(I,O∣λ)
对于条件随机场,它的解码任务即:找到一条合适的词性标注序列 y ^ ( i ) \hat {y}^{(i)} y^(i),使得 P ( y ^ ( i ) ∣ x 1 : T ( i ) ) \mathcal P(\hat {y}^{(i)} \mid \mathcal x_{1:T}^{(i)}) P(y^(i)∣x1:T(i))达到最大。数学符号表达如下:
y ^ ( i ) = arg max y ( i ) = ( y 1 ( i ) , ⋯ , y T ( i ) ) T P ( y ( i ) ∣ x ( i ) ) \hat {y}^{(i)} = \mathop{\arg\max}\limits_{y^{(i)} = (y_1^{(i)},\cdots,y_T^{(i)})^T} \mathcal P(y^{(i)} \mid x^{(i)}) y^(i)=y(i)=(y1(i),⋯,yT(i))TargmaxP(y(i)∣x(i))
- 通过联合概率分布,对边缘概率分布进行求解 (Marginal Probability):
关于条件随机场的推断任务(2022/11/16)
边缘概率分布
条件随机场的边缘概率分布求解可以总结为:
这里假定每一时刻的隐状态
y
t
(
i
)
(
t
=
1
,
2
,
⋯
,
T
)
y_t^{(i)}(t=1,2,\cdots,T)
yt(i)(t=1,2,⋯,T)的取值均为‘离散型随机变量’,其中每一种取值均有对应的概率结果,从而构成概率分布。
Given Model
(
θ
)
,
P
(
Y
=
y
(
i
)
∣
X
=
x
(
i
)
)
→
P
(
y
t
(
i
)
=
j
∣
x
(
i
)
)
\text{Given Model}(\theta) ,\mathcal P(\mathcal Y = y^{(i)} \mid \mathcal X = x^{(i)}) \to \mathcal P(y_t^{(i)} = j \mid x^{(i)})
Given Model(θ),P(Y=y(i)∣X=x(i))→P(yt(i)=j∣x(i))
回顾条件随机场的概率图表示,它是一个包含
T
T
T个极大团的马尔可夫随机场:
由于模型已知,因而各极大团的势函数也是已知项。
P
(
y
(
i
)
∣
x
(
i
)
)
=
P
(
y
1
(
i
)
,
y
2
(
i
)
,
⋯
,
y
T
(
i
)
∣
x
1
:
T
(
i
)
)
=
1
Z
∏
t
=
1
T
−
1
ψ
t
(
y
t
(
i
)
,
y
t
+
1
(
i
)
,
x
1
:
T
(
i
)
)
\begin{aligned} \mathcal P(y^{(i)} \mid x^{(i)}) & = \mathcal P(y_1^{(i)},y_2^{(i)},\cdots,y_T^{(i)} \mid x_{1:T}^{(i)})\\ & = \frac{1}{\mathcal Z} \prod_{t=1}^{T-1} \psi_t(y_{t}^{(i)},y_{t+1}^{(i)},x_{1:T}^{(i)}) \end{aligned}
P(y(i)∣x(i))=P(y1(i),y2(i),⋯,yT(i)∣x1:T(i))=Z1t=1∏T−1ψt(yt(i),yt+1(i),x1:T(i))
在求解某一项
y
t
(
i
)
(
t
=
1
,
2
,
⋯
,
T
)
y_t^{(i)}(t=1,2,\cdots,T)
yt(i)(t=1,2,⋯,T)时,需要将其他无关项积分掉:
P
(
y
t
(
i
)
∣
x
1
:
T
(
i
)
)
=
∑
y
1
(
i
)
,
⋯
,
y
t
−
1
(
i
)
,
y
t
+
1
(
i
)
,
⋯
,
y
T
(
i
)
P
(
y
(
i
)
∣
x
(
i
)
)
=
∑
y
1
(
i
)
,
⋯
,
y
t
−
1
(
i
)
∑
y
t
+
1
(
i
)
,
⋯
,
y
T
(
i
)
1
Z
∏
t
=
1
T
−
1
ψ
t
(
y
t
(
i
)
,
y
t
+
1
(
i
)
,
x
1
:
T
(
i
)
)
\begin{aligned} \mathcal P(y_t^{(i)} \mid x_{1:T}^{(i)}) & = \sum_{y_1^{(i)},\cdots,y_{t-1}^{(i)},y_{t+1}^{(i)},\cdots,y_{T}^{(i)}} \mathcal P(y^{(i)} \mid x^{(i)}) \\ & = \sum_{y_1^{(i)},\cdots,y_{t-1}^{(i)}} \sum_{y_{t+1}^{(i)},\cdots,y_T^{(i)}} \frac{1}{\mathcal Z} \prod_{t=1}^{T-1} \psi_t(y_{t}^{(i)},y_{t+1}^{(i)},x_{1:T}^{(i)}) \end{aligned}
P(yt(i)∣x1:T(i))=y1(i),⋯,yt−1(i),yt+1(i),⋯,yT(i)∑P(y(i)∣x(i))=y1(i),⋯,yt−1(i)∑yt+1(i),⋯,yT(i)∑Z1t=1∏T−1ψt(yt(i),yt+1(i),x1:T(i))
观察上式,这里假设隐状态
y
t
(
i
)
y_t^{(i)}
yt(i)的取值方式集合为
K
\mathcal K
K,集合中的每一种取值方式均需要执行
T
−
1
T-1
T−1次连乘操作,并且上式中一共包含
T
−
1
T-1
T−1个连加项,它的时间复杂度表示为:
∣
K
∣
|\mathcal K|
∣K∣表示为‘取值集合中的元素数量’。
O
(
∣
K
∣
T
−
1
)
⋅
O
(
T
−
1
)
=
O
[
(
T
−
1
)
∣
K
∣
T
−
1
]
O(|\mathcal K|^{T-1}) \cdot O(T-1) = O\left[(T-1) |\mathcal K|^{T-1}\right]
O(∣K∣T−1)⋅O(T−1)=O[(T−1)∣K∣T−1]
这种包含指数的复杂度是极难求解的。
边缘概率分布的简化过程
回顾上式,观察连乘部分:
∏
t
=
1
T
−
1
ψ
t
(
y
t
(
i
)
,
y
t
+
1
(
i
)
,
x
1
:
T
(
i
)
)
=
ψ
1
(
y
1
(
i
)
,
y
2
(
i
)
,
x
1
:
T
(
i
)
)
⋯
ψ
T
−
1
(
y
T
−
1
(
i
)
,
y
T
(
i
)
,
x
1
:
T
(
i
)
)
\prod_{t=1}^{T-1} \psi_t(y_t^{(i)},y_{t+1}^{(i)},x_{1:T}^{(i)}) = \psi_1(y_1^{(i)},y_2^{(i)},x_{1:T}^{(i)}) \cdots \psi_{T-1}(y_{T-1}^{(i)},y_T^{(i)},x_{1:T}^{(i)})
t=1∏T−1ψt(yt(i),yt+1(i),x1:T(i))=ψ1(y1(i),y2(i),x1:T(i))⋯ψT−1(yT−1(i),yT(i),x1:T(i))
发现:连乘中的每一项均只和两个相邻的隐状态相关,和其他隐状态无关。因此,可以将原式中的连加项带入到连乘部分的各项中。
其中
k
k
k是隐状态取值集合
K
\mathcal K
K的一种取值。
P
(
y
t
(
i
)
∣
x
1
:
T
(
i
)
)
=
1
Z
[
∑
y
1
(
i
)
,
⋯
,
y
t
−
1
(
i
)
∏
t
=
1
t
−
1
ψ
t
(
y
t
(
i
)
,
y
t
+
1
(
i
)
,
x
1
:
T
(
i
)
)
]
⋅
[
∑
y
t
+
1
(
i
)
,
⋯
,
y
T
(
i
)
∏
t
=
t
T
−
1
ψ
t
(
y
t
(
i
)
,
y
t
+
1
(
i
)
,
x
1
:
T
(
i
)
)
]
=
1
Z
[
∑
y
1
(
i
)
,
⋯
,
y
t
−
1
(
i
)
ψ
1
(
y
1
(
i
)
,
y
2
(
i
)
,
x
1
:
T
(
i
)
)
⋯
ψ
t
−
1
(
y
t
−
1
(
i
)
,
y
t
(
i
)
=
k
,
x
1
:
T
(
i
)
)
]
⋅
[
∑
y
t
+
1
(
i
)
,
⋯
,
y
T
(
i
)
ψ
t
(
y
t
(
i
)
=
k
,
y
t
+
1
(
i
)
,
x
1
:
T
(
i
)
)
⋯
ψ
T
−
1
(
y
T
−
1
(
i
)
,
y
T
(
i
)
,
x
1
:
T
(
i
)
)
]
\begin{aligned} \mathcal P(y_t^{(i)} \mid x_{1:T}^{(i)}) & = \frac{1}{\mathcal Z} \left[\sum_{y_1^{(i)},\cdots,y_{t-1}^{(i)}} \prod_{t=1}^{t-1} \psi_t(y_{t}^{(i)},y_{t+1}^{(i)},x_{1:T}^{(i)})\right] \cdot \left[\sum_{y_{t+1}^{(i)},\cdots,y_{T}^{(i)}} \prod_{t=t}^{T-1}\psi_t(y_{t}^{(i)},y_{t+1}^{(i)},x_{1:T}^{(i)})\right] \\ & = \frac{1}{\mathcal Z} \left[\sum_{y_1^{(i)},\cdots,y_{t-1}^{(i)}} \psi_1(y_1^{(i)},y_2^{(i)},x_{1:T}^{(i)}) \cdots \psi_{t-1}(y_{t-1}^{(i)},y_t^{(i)} = k,x_{1:T}^{(i)})\right] \cdot \left[\sum_{y_{t+1}^{(i)},\cdots,y_{T}^{(i)}}\psi_{t}(y_t^{(i)} = k,y_{t+1}^{(i)},x_{1:T}^{(i)}) \cdots \psi_{T-1}(y_{T-1}^{(i)},y_T^{(i)},x_{1:T}^{(i)})\right] \end{aligned}
P(yt(i)∣x1:T(i))=Z1⎣⎢⎡y1(i),⋯,yt−1(i)∑t=1∏t−1ψt(yt(i),yt+1(i),x1:T(i))⎦⎥⎤⋅⎣⎢⎡yt+1(i),⋯,yT(i)∑t=t∏T−1ψt(yt(i),yt+1(i),x1:T(i))⎦⎥⎤=Z1⎣⎢⎡y1(i),⋯,yt−1(i)∑ψ1(y1(i),y2(i),x1:T(i))⋯ψt−1(yt−1(i),yt(i)=k,x1:T(i))⎦⎥⎤⋅⎣⎢⎡yt+1(i),⋯,yT(i)∑ψt(yt(i)=k,yt+1(i),x1:T(i))⋯ψT−1(yT−1(i),yT(i),x1:T(i))⎦⎥⎤
-
首先观察第一个中括号项 Δ l e f t \Delta_{left} Δleft,针对这种 积分项与函数匹配的情况,使用变量消去法的方式进行化简:
变量消去法是精确推断的一种化简方式,欢迎回去考古。
Δ l e f t = ∑ y 1 ( i ) , ⋯ , y t − 1 ( i ) ψ 1 ( y 1 ( i ) , y 2 ( i ) , x 1 : T ( i ) ) ⋯ ψ t − 1 ( y t − 1 ( i ) , y t ( i ) = k , x 1 : T ( i ) ) = ∑ y 2 ( i ) , ⋯ , y t − 1 ( i ) ψ 2 ( y 2 ( i ) , y 3 ( i ) , x 1 : T ( i ) ) ⋯ ψ t − 1 ( y t − 1 ( i ) , y t ( i ) = k , x 1 : T ( i ) ) ∑ y 1 ( i ) ψ 1 ( y 1 ( i ) , y 2 ( i ) , x 1 : T ( i ) ) \begin{aligned} \Delta_{left} & = \sum_{y_1^{(i)},\cdots,y_{t-1}^{(i)}} \psi_1(y_1^{(i)},y_2^{(i)},x_{1:T}^{(i)}) \cdots \psi_{t-1}(y_{t-1}^{(i)},y_t^{(i)} = k,x_{1:T}^{(i)}) \\ & = \sum_{y_2^{(i)},\cdots,y_{t-1}^{(i)}} \psi_2(y_2^{(i)},y_3^{(i)},x_{1:T}^{(i)}) \cdots \psi_{t-1}(y_{t-1}^{(i)},y_t^{(i)} = k,x_{1:T}^{(i)}) \sum_{y_1^{(i)}} \psi_1(y_1^{(i)},y_2^{(i)},x_{1:T}^{(i)}) \end{aligned} Δleft=y1(i),⋯,yt−1(i)∑ψ1(y1(i),y2(i),x1:T(i))⋯ψt−1(yt−1(i),yt(i)=k,x1:T(i))=y2(i),⋯,yt−1(i)∑ψ2(y2(i),y3(i),x1:T(i))⋯ψt−1(yt−1(i),yt(i)=k,x1:T(i))y1(i)∑ψ1(y1(i),y2(i),x1:T(i)) -
此时, ∑ y 1 ( i ) ψ 1 ( y 1 ( i ) , y 2 ( i ) , x 1 : T ( i ) ) \sum_{y_1^{(i)}} \psi_1(y_1^{(i)},y_2^{(i)},x_{1:T}^{(i)}) ∑y1(i)ψ1(y1(i),y2(i),x1:T(i))会将 y 1 ( i ) y_1^{(i)} y1(i)积分掉,最终返回一个仅关于 y 2 ( i ) y_2^{(i)} y2(i)的函数:
m 1 ( y 2 ( i ) , x 1 : T ( i ) ) m_{1}(y_2^{(i)},x_{1:T}^{(i)}) m1(y2(i),x1:T(i))表示链式条件随机场中‘第1 1 1个极大团将’y 1 ( i ) y_1^{(i)} y1(i)积分掉后的函数结果。
∑ y 1 ( i ) ψ 1 ( y 1 ( i ) , y 2 ( i ) , x 1 : T ( i ) ) = m 1 ( y 2 ( i ) , x 1 : T ( i ) ) \sum_{y_1^{(i)}} \psi_1(y_1^{(i)},y_2^{(i)},x_{1:T}^{(i)}) = m_{1}(y_2^{(i)},x_{1:T}^{(i)}) y1(i)∑ψ1(y1(i),y2(i),x1:T(i))=m1(y2(i),x1:T(i)) -
最终, Δ l e f t \Delta_{left} Δleft继续表示为如下形式:
将第m 1 ( y 2 ( i ) , x 1 : T ( i ) ) m_{1}(y_2^{(i)},x_{1:T}^{(i)}) m1(y2(i),x1:T(i))与第2 2 2个极大团结合,继续进行积分。
∑ y 2 ( i ) ψ 2 ( y 2 ( i ) , y 3 ( i ) , x 1 : T ( i ) ) ⋅ m 1 ( y 2 ( i ) , x 1 : T ( i ) ) = m 1 → 2 ( y 3 ( i ) , x 1 : T ( i ) ) \sum_{y_2^{(i)}} \psi_2(y_2^{(i)},y_3^{(i)},x_{1:T}^{(i)}) \cdot m_1(y_2^{(i)},x_{1:T}^{(i)}) = m_{1 \to 2}(y_3^{(i)},x_{1:T}^{(i)}) y2(i)∑ψ2(y2(i),y3(i),x1:T(i))⋅m1(y2(i),x1:T(i))=m1→2(y3(i),x1:T(i))-
m
1
→
2
(
y
3
(
i
)
,
x
1
:
T
(
i
)
)
m_{1 \to 2}(y_3^{(i)},x_{1:T}^{(i)})
m1→2(y3(i),x1:T(i))
表示y 2 ( i ) y_2^{(i)} y2(i)被积分掉,消耗第1 1 1个极大团产生的关于第2 2 2个极大团的函数结果。
Δ l e f t = ∑ y 3 ( i ) , ⋯ , y t − 1 ( i ) ψ 3 ( y 3 ( i ) , y 4 ( i ) , x 1 : T ( i ) ) ⋯ ψ t − 1 ( y t − 1 ( i ) , y t ( i ) = k , x 1 : T ( i ) ) ⋅ ∑ y 2 ( i ) ψ 2 ( y 2 ( i ) , y 3 ( i ) , x 1 : T ( i ) ) ⋅ m 1 ( y 2 ( i ) , x 1 : T ( i ) ) = ∑ y 3 ( i ) , ⋯ , y t − 1 ( i ) ψ 3 ( y 3 ( i ) , y 4 ( i ) , x 1 : T ( i ) ) ⋯ ψ t − 1 ( y t − 1 ( i ) , y t ( i ) = k , x 1 : T ( i ) ) ⋅ m 1 → 2 ( y 3 ( i ) , x 1 : T ( i ) ) = ⋯ = ∑ y t − 1 ( i ) ψ t − 1 ( y t − 1 ( i ) , y t ( i ) = k , x 1 : T ( i ) ) ⋅ m ( t − 3 ) → ( t − 2 ) ( y t − 1 ( i ) , x 1 : T ( i ) ) = m ( t − 2 ) → ( t − 1 ) ( y t ( i ) = k , x 1 : T ( i ) ) \begin{aligned} \Delta_{left} & = \sum_{y_3^{(i)},\cdots,y_{t-1}^{(i)}} \psi_3(y_3^{(i)},y_4^{(i)},x_{1:T}^{(i)}) \cdots \psi_{t-1}(y_{t-1}^{(i)},y_t^{(i)} = k,x_{1:T}^{(i)}) \cdot \sum_{y_2^{(i)}} \psi_2(y_2^{(i)},y_3^{(i)},x_{1:T}^{(i)}) \cdot m_1(y_2^{(i)},x_{1:T}^{(i)}) \\ & = \sum_{y_3^{(i)},\cdots,y_{t-1}^{(i)}} \psi_3(y_3^{(i)},y_4^{(i)},x_{1:T}^{(i)}) \cdots \psi_{t-1}(y_{t-1}^{(i)},y_t^{(i)} = k,x_{1:T}^{(i)}) \cdot m_{1\to 2}(y_3^{(i)},x_{1:T}^{(i)}) \\ & = \cdots \\ & = \sum_{y_{t-1}^{(i)}} \psi_{t-1}(y_{t-1}^{(i)},y_{t}^{(i)} = k,x_{1:T}^{(i)}) \cdot m_{(t-3) \to (t-2)}(y_{t-1}^{(i)},x_{1:T}^{(i)}) \\ & = m_{(t-2) \to (t-1)}(y_t^{(i)} = k,x_{1:T}^{(i)}) \end{aligned} Δleft=y3(i),⋯,yt−1(i)∑ψ3(y3(i),y4(i),x1:T(i))⋯ψt−1(yt−1(i),yt(i)=k,x1:T(i))⋅y2(i)∑ψ2(y2(i),y3(i),x1:T(i))⋅m1(y2(i),x1:T(i))=y3(i),⋯,yt−1(i)∑ψ3(y3(i),y4(i),x1:T(i))⋯ψt−1(yt−1(i),yt(i)=k,x1:T(i))⋅m1→2(y3(i),x1:T(i))=⋯=yt−1(i)∑ψt−1(yt−1(i),yt(i)=k,x1:T(i))⋅m(t−3)→(t−2)(yt−1(i),x1:T(i))=m(t−2)→(t−1)(yt(i)=k,x1:T(i))
-
如果简化过程中保留积分的简化过程, Δ l e f t \Delta_{left} Δleft表示为如下形式:
给Δ l e f t \Delta_{left} Δleft定义一个符号:α t ( k ) \alpha_t(k) αt(k)。
α t ( k ) = ∑ y t − 1 ( i ) ψ t − 1 ( y t − 1 ( i ) , y t ( i ) = k , x 1 : T ( i ) ) ⋯ ∑ y 2 ( i ) ψ 2 ( y 2 ( i ) , y 3 ( i ) , x 1 : T ( i ) ) ∑ y 1 ( i ) ψ 1 ( y 1 ( i ) , y 2 ( i ) , x 1 : T ( i ) ) \alpha_t(k) =\sum_{y_{t-1}^{(i)}} \psi_{t-1}(y_{t-1}^{(i)},y_{t}^{(i)} = k,x_{1:T}^{(i)}) \cdots \sum_{y_2^{(i)}} \psi_2(y_2^{(i)},y_3^{(i)},x_{1:T}^{(i)})\sum_{y_1^{(i)}} \psi_1(y_1^{(i)},y_2^{(i)},x_{1:T}^{(i)}) αt(k)=yt−1(i)∑ψt−1(yt−1(i),yt(i)=k,x1:T(i))⋯y2(i)∑ψ2(y2(i),y3(i),x1:T(i))y1(i)∑ψ1(y1(i),y2(i),x1:T(i))
其他时刻的表示方法同理。如 α t − 1 ( j ) \alpha_{t-1}(j) αt−1(j):
α t − 1 ( j ) = ∑ y t − 2 ( i ) ψ t − 2 ( y t − 2 ( i ) , y t − 1 ( i ) = j , x 1 : T ( i ) ) ⋯ ∑ y 2 ( i ) ψ 2 ( y 2 ( i ) , y 3 ( i ) , x 1 : T ( i ) ) ∑ y 1 ( i ) ψ 1 ( y 1 ( i ) , y 2 ( i ) , x 1 : T ( i ) ) \alpha_{t-1}(j) = \sum_{y_{t-2}^{(i)}} \psi_{t-2}(y_{t-2}^{(i)},y_{t-1}^{(i)} = j,x_{1:T}^{(i)}) \cdots \sum_{y_2^{(i)}} \psi_2(y_2^{(i)},y_3^{(i)},x_{1:T}^{(i)})\sum_{y_1^{(i)}} \psi_1(y_1^{(i)},y_2^{(i)},x_{1:T}^{(i)}) αt−1(j)=yt−2(i)∑ψt−2(yt−2(i),yt−1(i)=j,x1:T(i))⋯y2(i)∑ψ2(y2(i),y3(i),x1:T(i))y1(i)∑ψ1(y1(i),y2(i),x1:T(i))
那么 α t ( k ) \alpha_t(k) αt(k)与 α t − 1 ( j ) \alpha_{t-1}(j) αt−1(j)之间的关联关系表示如下:
再强调一下,K \mathcal K K是隐状态离散的取值集合,j , k ∈ K j,k \in \mathcal K j,k∈K,完全可以通过迭代方式求解α t ( k ) \alpha_t(k) αt(k)。
α t ( k ) = ∑ y t − 1 ( i ) ψ t − 1 ( y t − 1 ( i ) = j , y t ( i ) = k , x 1 : T ( i ) ) ⋅ α t − 1 ( j ) = ∑ j ∈ K ψ t − 1 ( y t − 1 ( i ) = j , y t ( i ) = k , x 1 : T ( i ) ) ⋅ α t − 1 ( j ) \begin{aligned} \alpha_t(k) & = \sum_{y_{t-1}^{(i)}} \psi_{t-1}(y_{t-1}^{(i)}=j,y_t^{(i)}=k,x_{1:T}^{(i)}) \cdot \alpha_{t-1}(j) \\ & = \sum_{j \in \mathcal K} \psi_{t-1}(y_{t-1}^{(i)}=j,y_t^{(i)}=k,x_{1:T}^{(i)}) \cdot \alpha_{t-1}(j) \end{aligned} αt(k)=yt−1(i)∑ψt−1(yt−1(i)=j,yt(i)=k,x1:T(i))⋅αt−1(j)=j∈K∑ψt−1(yt−1(i)=j,yt(i)=k,x1:T(i))⋅αt−1(j)
第二个中括号项
Δ
r
i
g
h
t
\Delta_{right}
Δright同理,定义为
β
t
(
m
)
\beta_t(m)
βt(m),表示如下:
β
t
(
m
)
=
∑
y
t
+
1
(
i
)
ψ
t
(
y
t
(
i
)
=
m
,
y
t
+
1
(
i
)
,
x
1
:
T
(
i
)
)
∑
y
t
+
2
(
i
)
ψ
t
+
1
(
y
t
+
1
(
i
)
,
y
t
+
2
(
i
)
,
x
1
:
T
(
i
)
)
⋯
∑
y
T
(
i
)
ψ
T
−
1
(
y
T
−
1
(
i
)
,
y
T
(
i
)
,
x
1
:
T
(
i
)
)
\beta_t(m) = \sum_{y_{t+1}^{(i)}} \psi_{t}(y_{t}^{(i)} = m,y_{t+1}^{(i)},x_{1:T}^{(i)})\sum_{y_{t+2}^{(i)}} \psi_{t+1}(y_{t+1}^{(i)},y_{t+2}^{(i)},x_{1:T}^{(i)}) \cdots \sum_{y_T^{(i)}} \psi_{T-1}(y_{T-1}^{(i)},y_{T}^{(i)},x_{1:T}^{(i)})
βt(m)=yt+1(i)∑ψt(yt(i)=m,yt+1(i),x1:T(i))yt+2(i)∑ψt+1(yt+1(i),yt+2(i),x1:T(i))⋯yT(i)∑ψT−1(yT−1(i),yT(i),x1:T(i))
最终,求解边缘概率分布结果
P
(
y
t
(
i
)
∣
x
1
:
T
(
i
)
)
\mathcal P(y_t^{(i)} \mid x_{1:T}^{(i)})
P(yt(i)∣x1:T(i)):
P
(
y
t
(
i
)
∣
x
1
:
T
(
i
)
)
=
1
Z
⋅
α
t
(
k
)
⋅
β
t
(
m
)
\mathcal P(y_t^{(i)} \mid x_{1:T}^{(i)}) = \frac{1}{\mathcal Z} \cdot \alpha_t(k) \cdot \beta_t(m)
P(yt(i)∣x1:T(i))=Z1⋅αt(k)⋅βt(m)
简单总结
- 关于链式条件随机场的前向后向算法本质上就是不同方向的变量消去法,通过前后向的特征不断积分、融合,最终得到求解时刻的边缘概率结果;
- 上述边缘概率求解方法是基于结构最简单的链式条件随机场,如果条件随机场的格式复杂,对变量消除法进行延伸。如信念传播(Belief Propagation)。
相关参考:
机器学习-周志华著
机器学习-条件随机场(6)-CRF模型-要解决的问题
机器学习-条件随机场(7)-CRF模型-Inference-边缘概率计算
相关文章
- 神经网络与机器学习 笔记—Rosenblatt感知器收敛算法C++实现
- 机器学习框架ML.NET学习笔记【1】基本概念与系列文章目录
- [吴恩达机器学习笔记]15非监督学习异常检测4-6构建与评价异常检测系统
- [吴恩达机器学习笔记]11机器学习系统设计5数据量对机器学习的影响
- 机器学习数学笔记|微积分梯度jensen不等式
- 机器学习笔记之谱聚类(三)模型的矩阵形式转化
- 机器学习笔记之谱聚类(一)k-Means聚类算法介绍
- 机器学习笔记之条件随机场(一)背景介绍
- 机器学习笔记之卡尔曼滤波(一)动态模型基本介绍
- 机器学习笔记之概率图模型(十)因子图
- 机器学习笔记之概率图模型(四)基于贝叶斯网络的模型概述
- 机器学习笔记之降维(三)从最大投影方差角度观察主成分分析
- 机器学习笔记之降维(一)维数灾难
- 机器学习笔记之高斯混合模型(三)EM算法求解高斯混合模型(E步操作)
- 机器学习笔记之EM算法(三)隐变量与EM算法的本质
- Andrew Ng机器学习公开课笔记 -- 学习理论
- 机器学习笔记——皮尔逊相关系数
- [Amazon]人工智能入门学习笔记---AI-机器学习-深度学习

