【算法设计与分析】再探大O渐近表示法 | 增长顺序 | Big O | Big Omega | Big Order

目录

Ⅰ. 前置知识：算法复杂度

0x00 衡量算法的好坏

0x01 算法的复杂度

0x02 时间复杂度的概念

0x03 大O渐进表示法

0x04 时间复杂度计算的实例

Ⅱ. Order of Algorithms 

0x00 再探大O渐进表示法

0x01 常见复杂度函数增长率表

0x02 比较增长顺序（Comparing Orders of Growth）

0x03 Omega ​

0x04 Order ​

0x05 大O、Omega、Order

0x06 最坏情况和平均情况时间复杂度对比

0x07 Sums of powers & Groth rates

0x08 运行时间分析

0x09 算法设计例子

0x0A  Maximum Sum Subrectangle in 2D Array（二维数组中的最大和子矩阵）

---

Ⅰ. 前置知识：算法复杂度

0x00 衡量算法的好坏

❓ 如何衡量一个算法的好坏？看代码是否简洁？

💬 比如对于以下斐波那契数列：

long long Fib(int n) {
    if (n < 3) {
        return 1;
    }
    return Fib(n - 1) + Fib(n - 2);
}

🤔 不难发现，斐波那契数列使用递归方式实现时代码非常简洁，但代码简洁就一定好吗？我们该如何去衡量他的好坏呢？让我们带着问题我们继续往下看。

0x01 算法的复杂度

📚 介绍：算法在编写成可执行程序后，运行时需要耗费 时间资源 和 空间资源（即内存资源）。因此，衡量一个算法的好坏一般是从 "时间" 和 "空间" 两个维度来衡量的，即 时间复杂度 和 空间复杂度 ：

     ① 时间复杂度：主要衡量一个算法的运行快慢。

     ② 空间复杂度：主要衡量一个算法运行所需要的额外空间。

0x02 时间复杂度的概念

📚 时间复杂度的定义：在计算机科学中，算法的时间复杂度是一个函数（这里的函数时数学里的函数，数学里面带有未知数的函数表达式），它定量描述了该算法的运行时间。一个算法执行所耗费的时间，从理论上来说其实是不能算出来的，只有你把你的程序放在机器上跑起来才能知道耗费了多少时间。但是把每个算法都跑一遍是非常不现实的事，所以就产生了时间复杂度这样的分析方式。一个算法所花费的时间与其中语句的执行次数成正比例，算法中的基本操作的执行次数，为算法的时间复杂度。

❓ 该如何计算时间复杂度呢？

🔑 简单来说就是：找到某条基本语句与问题规模 N 之间的数学表达式，就是算出了该算法的时间复杂度。

💬 例子：计算一下 Func1 中 ++count 语句总共执行了多少次？

void Func1(int N) {
    int count = 0;
    for (int i = 0; i < N; ++i) {
        for (int j = 0; j < N; j++) {
            ++count;
        }
    }

    for (int k = 0; k < 2 * N; ++k) {
        ++count;
    }

    int M = 10;
    while (M--) {
        ++count;
    }

    printf("%d\n", count);
}

🔑 Func1 执行的基本操作次数如下：

     N = 10            F(N) = 130

     N = 100          F(N) = 10210

     N = 1000        F(N) = 1002010

💡  N 越大，后两项对结果的影响就越小，所以我们也不需要精确的计算出结果，算个大概就可以了。所以这里我们将使用 大O渐进表示法 进行表示。

0x03 大O渐进表示法

【百度百科】大O符号（Big O notation）是用于描述函数渐进行为的数学符号。更确切地说，它是用另一个（通常更简单的）函数来描述一个函数数量级的渐近上界。在数学中，它一般用来刻画被截断的无穷级数尤其是渐近级数的剩余项。在计算机科学中，它在分析算法复杂性的方面非常有用。

📚 定义：大O符号是用于描述函数渐进性为的数学符号。

📚 推导大O阶方法：

① 用 常数1 取代运行时间中的所有加法常数。

② 在修改后的运行次数函数中，只保留最高阶项。

③ 如果最高阶 存在且不是1 ，则去除与这个项目相乘的常数。最后得到的结果就是大O阶。

🔑 使用大O渐进表示法后，Func1 的时间复杂度为 O(N^2) ：

↓

     N = 10            F(N) = 100

     N = 100          F(N) = 10000

     N = 1000        F(N) = 1000000

   （看到大O就知道这里面的值不是准确的值，而是大概值）

📌 注意事项：

① 一般情况下，时间复杂度计算式未知数都是用的 N，但是也可以是 M、K、X 等等其他的，如果出现其他字母（非N）的情况情况我们可以这么表示：

     如果 M 远大于 N  → O(M)

     如果 N 远大于 M  → O(N)

     M 和 N 差不多大  → O(M + N)

② O(1) 不是代表算法运行一次，而是 "常数次" 。

💡 通过上面的例子，我们发现大O渐进表示法去掉了那些对结果影响不大的项，简洁明了的表示出了执行次数。

📚 另外有些算法的时间复杂度存在最好情况、平均情况、最坏情况：

     ① 最好情况：任意输入规模的最小运行次数（下界）
     ② 平均情况：任意输入规模的期望运行次数
     ③ 最坏情况：任意输入规模最大的运行次数（上界）

时间复杂度是一个悲观的预期，当一个算法随着输入不同、时间复杂度不同，做一个悲观的预期，看最坏的情况！

💬 例子：在一个长度为N的数组（下面例题中会出现，先提前讲个大概）

      ① 最好情况：1 次找到

      ② 最坏情况：N 次找到

      ③ 平均情况：N/2 次找到

📚 在实际中，一般情况下我们主要关注的是算法的最坏运行情况，所以数组中搜索数据时间复杂度为O(N) 。当然，这不是绝对的！比如希尔排序很少出现最坏的情况，所以有时候我们也会看平均情况。

0x04 时间复杂度计算的实例

💬 实例1：计算 Func2 的时间复杂度

void Func2(int N) {
    int count = 0;
    for (int k = 0; k < 2 * N ; ++ k) {
        ++count;
    }

    int M = 10;
    while (M--) {
        ++count;
    }
    
    printf("%d\n", count);
}

💡 答案：O(N) 

🔑 解析：基本操作执行了 2N+10 次，通过推导大O阶方法知道，时间复杂度为 O(N) 。因为当N越大，对10的影响就越小，所以+10省略。并且2N根据第三条规则（前面讲了），相乘时不是1时系数忽略，所以使用大O渐进法表示结果如下：

↓

我们带到题里再看一遍规则：

① 用常数1取代运行时间中的所有加法常数。

② 在修改后的运行次数函数中，只保留最高阶项。

③ 如果最高阶存在且不是1 ，则去除与这个项目相乘的常数。 

❓ 为什么不算 ++k ？

🔑 我们不需要算的那么精确，我们只需要算循环的次数，指的是算法逻辑走了多少次，而不是程序走了多少条指令。所以我们不需要考虑 ++k 。

💬 实例2：计算 Func3 的时间复杂度

void Func3(int N, int M) {
    int count = 0;
    for (int k = 0; k < M; ++ k) {
        ++count;
    }
    
    for (int k = 0; k < N ; ++ k) {
        ++count;
    }

    printf("%d\n", count);
}

💡 答案：O(M + N)

🔑 解析：基本操作执行了M+N次，有两个未知数M和N，时间复杂度为 O(M+N）。一般情况下时间复杂度计算时未知数用的是N，但是也可以用其他未知数表示（前面讲过），所以使用大O渐进法表示结果如下：

为了加深印象，我们再看一遍：

一般情况下，时间复杂度计算式未知数都是用的 N，但是也可以是 M、K、X 等等其他的，如果出现其他字母（非N）的情况情况我们可以这么表示：

若   → 

若   → 

若     → 

💬 实例3：计算 Func4 的时间复杂度

void Func4(int N) {
    int count = 0;
    for (int k = 0; k < 100; ++ k) {
        ++count;
    }

    printf("%d\n", count);
}

💡 答案：O(1)

🔑 解析：基本操作执行了10次，通过推到大N阶的方法，时间复杂度为O(1) 。值得注意的是，这里的 "1" 是常数次而不是代表算法运行1次。所以使用大O渐进法表示结果如下：

↓

💬 实例4：计算 strchr 的时间复杂度

// 计算strchr的时间复杂度？
const char * strchr ( const char * str, int character );

💡 答案：O(N)

🔑 解析：基本操作执行最好1次，最坏N次。因为时间复杂度一般取最坏，所以时间复杂度为O(N) 。使用大O渐进法表示结果如下：

↓

 

💬 实例5：计算 BubbleSort 的时间复杂度

void BubbleSort(int* a, int n) {
    assert(a);
    for (size_t end = n; end > 0; --end) {
    int exchange = 0;
        for (size_t i = 1; i < end; ++i) {
            if (a[i-1] > a[i]) {
                Swap(&a[i-1], &a[i]);
                exchange = 1;
            }
        }

        if (exchange == 0) {
            break;
        }
    }
}

💡 答案：O(N^2)

🔑 解析：基本操作执行最好N次，最坏执行了(N*(N+1)/2次，通过推导大O阶方法+时间复杂度一般看最坏，时间复杂度为 O(N^2) 。冒泡排序，前一个比后一个大就交换。这两个循环虽然嵌套在一起，但是里面的循环不是n，外面的循环也不是n，而是end，它是在变化的。{ N-1 N-2 N-3 ... 1 }  ，所以他是个等差数列，使用大O渐进法表示结果如下：

↓

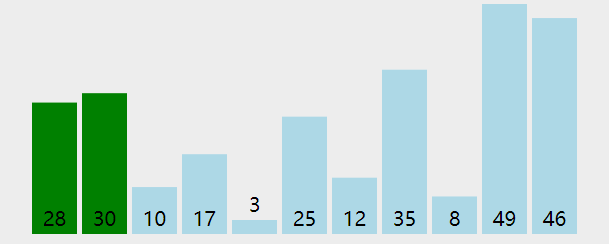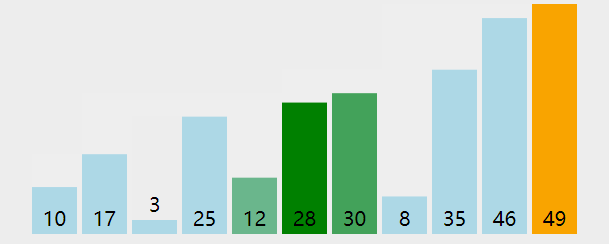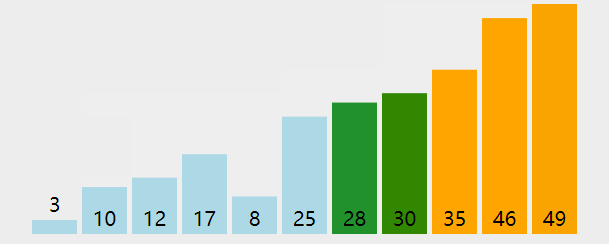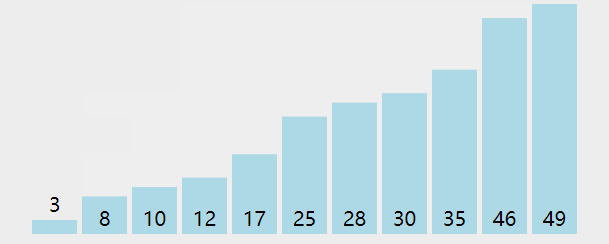
💬 实例6：计算 BinarySearch 的时间复杂度

int BinarySearch(int* a, int n, int x) {
    assert(a);
    int begin = 0;
    int end = n - 1;
    while (begin < end) {
        int mid = begin + ((end-begin) >> 1);
        if (a[mid] < x)
            begin = mid + 1;
        else if (a[mid] > x)
            end = mid;
        else
            return mid;
    }

    return -1;
}

💡 答案：O(logN)

🔑 解析：基本操作执行最好1次，最坏O(logN)次，时间复杂度为O(logN）。使用大O渐进法表示结果如下：

在这里，我不得不吹一下二分查找了，真的是个非常牛掰的算法！

N个数中查找          大概查找次数

1000                       10

100W                      20

1亿                          30

......

在中国14亿人口中查找一个人，最多只要31次就可以了！当然，二分查找查找对象前提是有序的。

💬 实例7：计算递归版阶乘 Fac 的时间复杂度

long long Fac(size_t N)
{
    if (0 == N)
        return 1;
    return Fac(N - 1) * N;
}

💡 答案：O(N)

🔑 解析：通过计算分析发现基本操作递归了N次，时间复杂度为O(N) 。使用大O渐进法表示结果如下：

📚 递归算法：递归次数 * 每次递归调用次数

💬 实例8：计算递归版斐波那契数 Fib 的时间复杂度

long long Fib(size_t N) {
    if(N < 3)
        return 1;
    return Fib(N-1) + Fib(N-2);
}

💡 答案：O(2^N)

🔑 解析：通过计算分析发现基本操作递归了2^N次，时间复杂度为O(2^N) 。使用大O渐进法表示结果如下：

Ⅱ. Order of Algorithms

0x00 渐近上界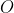 

当函数的大小只有上界，没有明确下界的时，则可使用大  表示法，该渐进描述符一般用于描述算法的 最坏复杂度。

给定两函数 ，， 存在一些正的实数常数  和一些非负的整数 

譬如， for all ，我们称  是  的大 ，举个例子：

x = x = 1
for (i = 1; i <= n; i++)
    y = y + 2;
for (i = 0; i >= 1; i--)
    for (j = n; j >= 1; j--)
        z = z + 1

时间复杂度为：

具体计算过程如下：

注1：大  为一个函数设定了一个渐近（Asymptotic）的上界。

严格的上限：

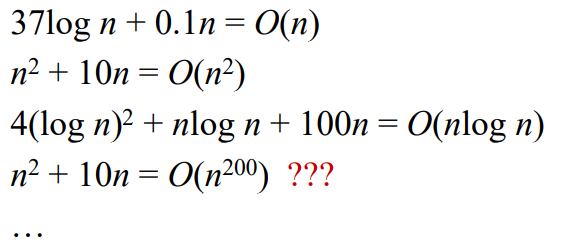
0x01 常见复杂度函数增长率表

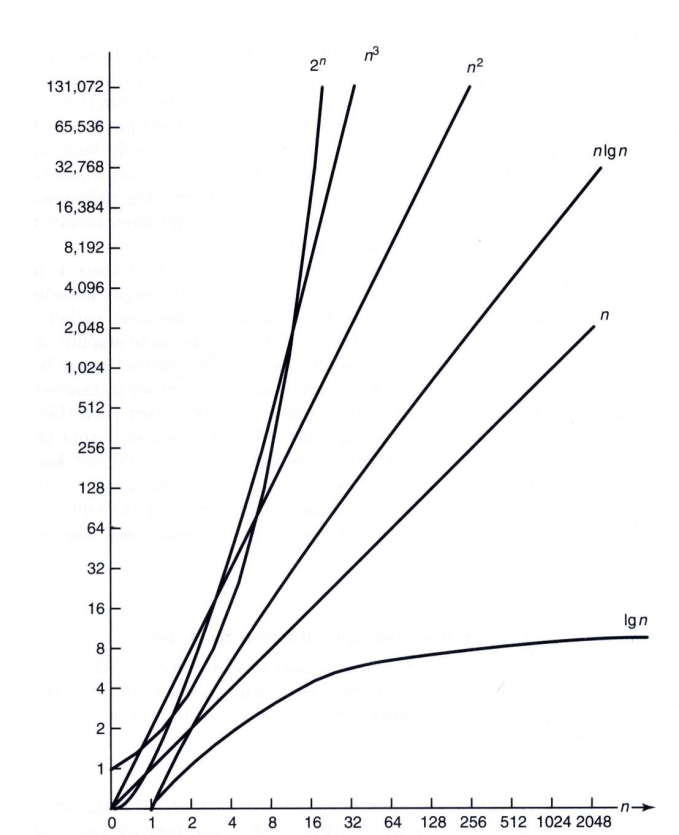
注2：给定一个消耗函数 ，如何找到适当的复杂度函数 ，使  （默认抑制低阶项和常数因子）？

0x02 比较增长顺序（Comparing Orders of Growth）

计算两个函数的极限比，是比较两个函数的增长顺序的一种可行的方法：

0x03 渐近下界 Omega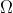 

当函数的大小只有下界，没有明确的上界的时，可使用大  表示法，该渐进描述符一般用于描述算法的 最优复杂度 。

给定两个函数，，当且仅当存在一些正实数常数  和一些非负的整数 ，例如 。

我们称  是  的 Omega

 给函数设置了一个渐近的下界，大于等于。

例如：

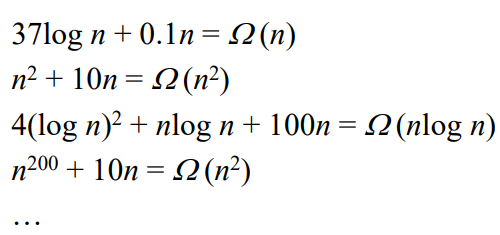
0x04 确界 Order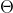 

  需同时满足大  和 ，故称为确界。当一个算法有明确上界和明确下界时，则可以使用大  表示法。

给定两个函数  当且仅当  和 

那么， 当且仅当如果存在正实数常数 ， 和  是一些非负整数 n，例如 for all

。

我们称   是   的 

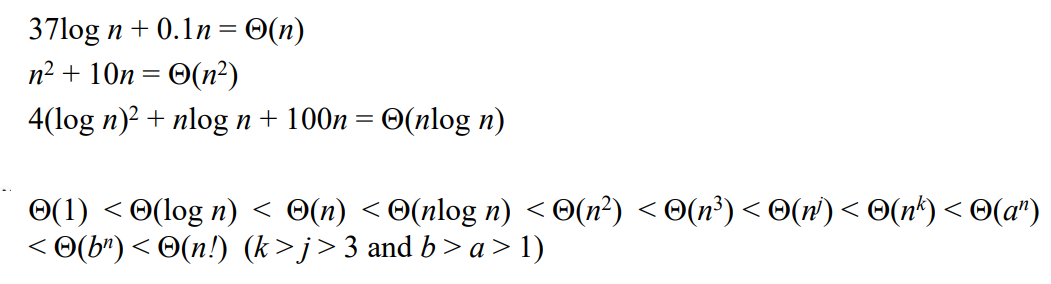
0x05 总结：大O、大Ω、大Θ

 表示渐进上界， 表示渐进下界， 则需同时满足大  和 ，故称为确界。

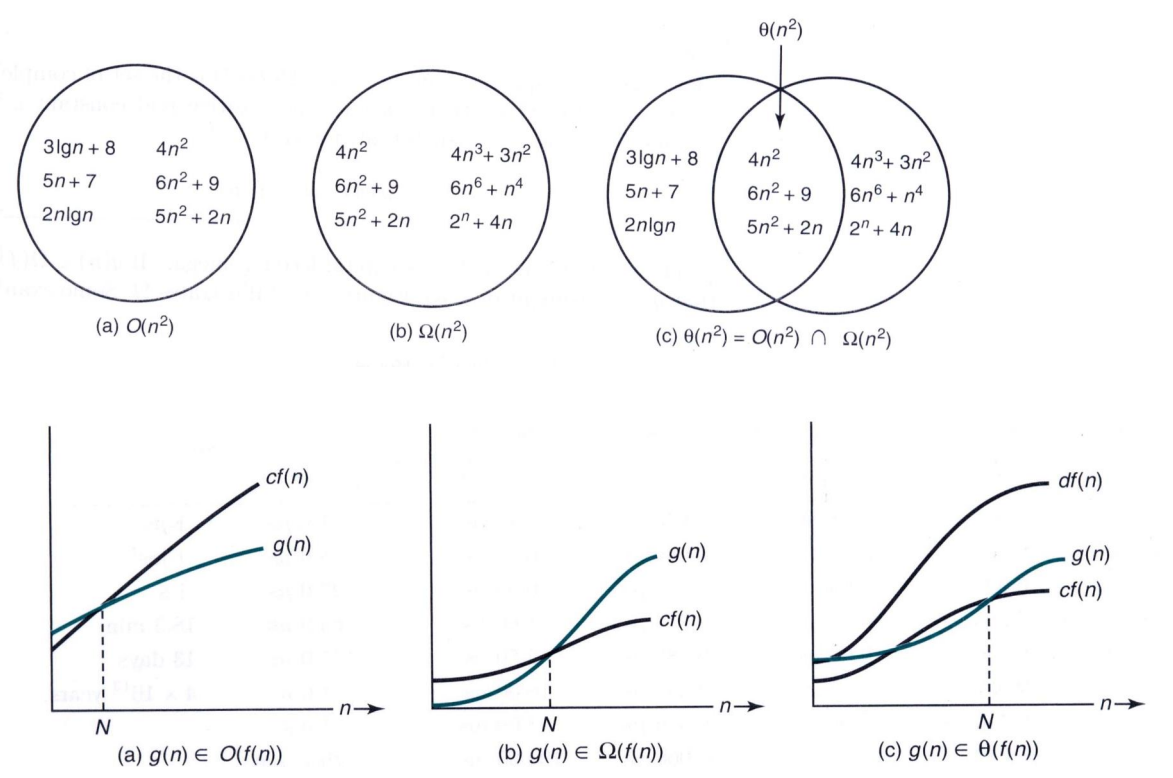
 给定时间复杂度的算法执行时间：

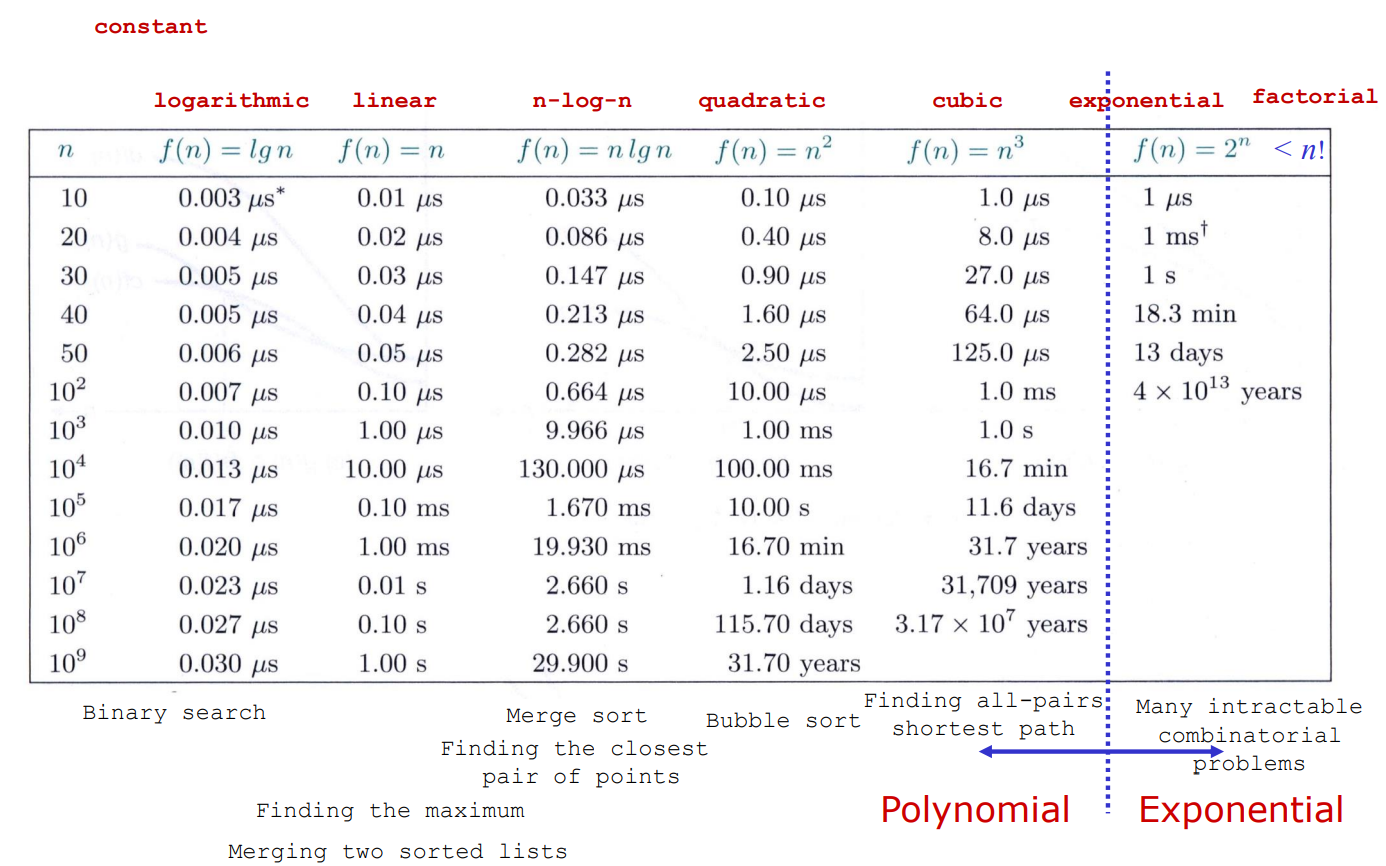
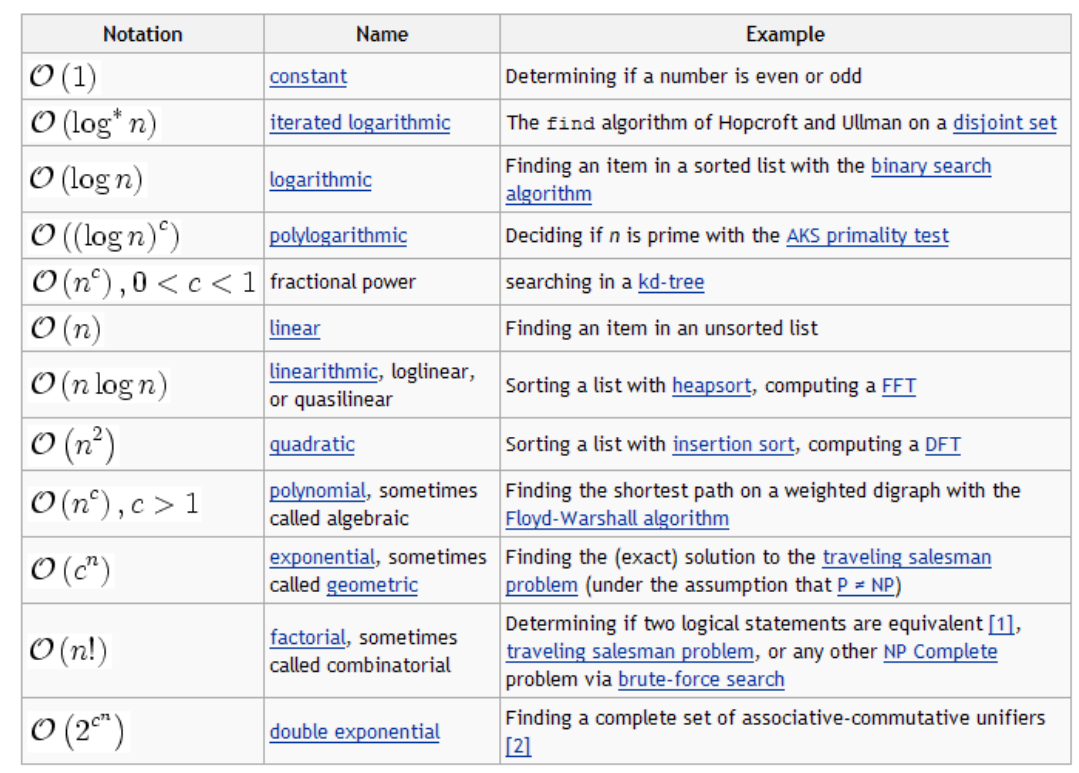
0x06 最坏情况和平均情况时间复杂度对比

期望值：

 ：大小 为  的所有输入的集合

 ：输入   的算法成本

 ：输入  发生的概率

最坏情况复杂度：

平均情况复杂度：

快速排序算法最坏情况为  ，平均情况为 

0x07 Sums of powers & Groth rates

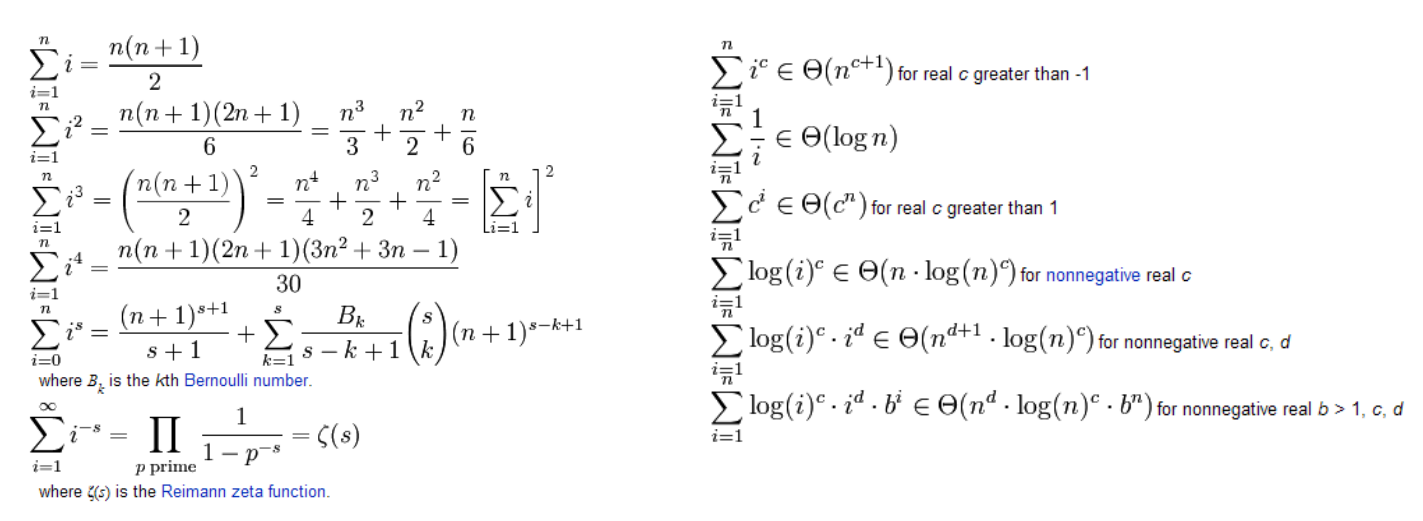
0x08 运行时间分析

x = x + 1;
for (i = 1; i <= n; i++)
    y = y + 2;
for (i = n; i >=1; i--)
    for (j = n; j >= 1; j--)
        z = z + 1; 

 时间复杂度：

c = 0; // n > 0
for (i = 1; i <= n; i++)
    for (j = 1; j <= n; j++)
        for (k = 1; k <= n; k = k*2)
            c += 2;

时间复杂度： 

i = 1; j = 1; m = 0; // n > 0
while (j <= n) {
    i++;
    j = j + i;
    m = m + 2;
}

时间复杂度：

0x09 算法设计例子

Maximum Subsequence Sum (MSS) Problem

最大后缀和问题

给定 （可能是复数）整数 ，找到  的最大值

例子：

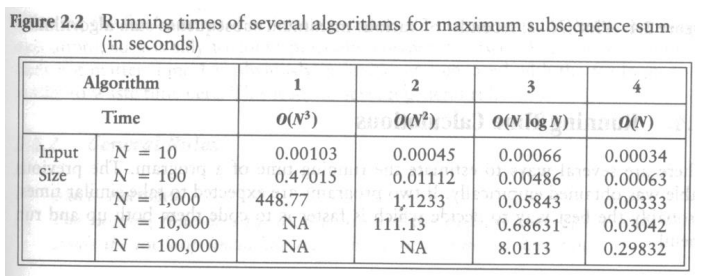
子序列的最大和与最大子序列和

Three Approaches for Max. Subsequence Sum Problem

Approach I: Simple Counting

0x0A  Maximum Sum Subrectangle in 2D Array（二维数组中的最大和子矩阵）

Problem：Given an mxn array of integers, find a subrectangle with the largest sum. (In this problem, we assume that a subrectangle is any contiguous sub-array of size 1x1 or greater located within the whole array.)

Note：

What is the input size of this problem？ → (m, n)

• If m = n → n

How many subrectangles are there in an mxn array？

How many subrectangles are there in an mxn array？

 

 

📌 [ 笔者 ]   王亦优
📃 [ 更新 ]   2022.9.14
❌ [ 勘误 ]   /* 暂无 */
📜 [ 声明 ]   由于作者水平有限，本文有错误和不准确之处在所难免，
              本人也很想知道这些错误，恳望读者批评指正！

📜 参考资料  - R. Neapolitan, Foundations of Algorithms (5th ed.), Jones & Bartlett, 2015. - T. Cormen《算法导论》（第三版），麻省理工学院出版社，2009年。 - T. Roughgarden, Algorithms Illuminated, Part 1~3, Soundlikeyourself Publishing, 2018. - A. Aho, J. Hopcroft, and J. Ullman, Design and Analysis of Algorithms, Addison-Wesley, 1974. - M. Weiss, Data Structure and Algorithm Analysis in C (2nd ed.), Pearson, 1997. - A. Levitin, Introduction to the Design and Analysis of Algorithms, Addison Wesley, 2003. - A. Aho, J. Hopcroft, and J. Ullman, Data Structures and Algorithms, Addison-Wesley, 1983. - E. Horowitz, S. Sahni and S. Rajasekaran, Computer Algorithms/C++, Computer Science Press, 1997. - R. Sedgewick, Algorithms in C: 第1-4部分（第三版），Addison-Wesley，1998 - R. Sedgewick，《C语言中的算法》。第5部分（第3版），Addison-Wesley，2002​​​​​​​ - J. Kleinberg&E. Tardos, Algorithm Design, Addison Wesley, 2005. - R. Sedgewick&K. Wayne，《算法》（第四版），Addison-Wesley，2011 - S. Dasgupta，《算法》，McGraw-Hill教育出版社，2006。 - S. Baase&A. Van Gelder, Computer Algorithms: 设计与分析简介》，Addison Wesley，2000。 - E. Horowitz，《C语言中的数据结构基础》，计算机科学出版社，1993 - S. Skiena, The Algorithm Design Manual (2nd ed.), Springer, 2008.