C++算法之巧解数学问题

巧解数学问题

利用C++求解经典数学问题

1.公倍数与公因数

利用辗转相除法，我们可以很方便地求得两个数的最大公因数（greatest common divisor，gcd）；将两个数相乘再除以最大公因数即可得到最小公倍数（least common multiple, lcm）。
首先介绍一下辗转相除法：

#include<iostream>
#include<cstdio>
using namesapce std;

int fun(int m,int n)
{
    int rem;//余数，当余数为零的时候，最后的m即为最大公约数
    //先用较小的数对较大的数取余，再用余数对较小的数取余，直到余数为零
    while(n>0)
    {
        rem=m%n;
        m=n;
        n=rem;
     }
     return m;//将结果返回
 }

int main(){
	int n,m;
	cin>>m>>n;
	cout<<"m和n的最大公约数为："<<fun(m,n)<<endl;
	return 0; 
}    

//简化一下，用递归来求
int fun(int m,int n)
{
    if(n==0) return m;
    return (fun(n,m%n);
}

//再简化一下
int gcd(int m,int n){
    return n ? gcd(n,m%n):m;
}

题解：

int gcd(int a,int b)
{
    return b==0 ? a:gcd(b,a%b);
}
int lcm(int a,int b)
{
    return a*b/gcd(a,b);
}

进一步地，我们也可以通过扩展欧几里得算法（extended gcd）在求得 a 和 b 最大公因数的同时，也得到它们的系数 x 和 y，从而使 ax + by = gcd(a, b)。

int xGCD(int a,int b,int &x,int &y)
{
    if(!b){
        x=1,y=0;
        return 0;
    }
    int x1,y1,gcd=xGCD(b,a%b,x1,y1);
    x=y1,y=x1-(a/b)*y1;
    return gcd;
}

2.质数

质数又称素数，指的是在大于1的自然数中，除了1和他本身以外不再有其他因数的自然数，值得注意的是，每一个数都可以分解成质数的乘积。

埃拉托斯特尼筛法（Sieve of Eratosthenes，简称埃氏筛法）是非常常用的，判断一个整数是否是质数的方法。并且它可以在判断一个整数 n 时，同时判断所小于 n 的整数，因此非常适合这道题。其原理也十分易懂：从 1 到 n 遍历，假设当前遍历到 m，则把所有小于 n 的、且是 m 的倍数的整数标为和数；遍历完成后，没有被标为和数的数字即为质数。

int countPrimes(int n)
{
    if(n<=2) return 0;
    vector<bool>prime(n,true);
    int count=n-2;//去掉不是质数的1
    for(int i=2;i<=n;++i)
    {
        if(prime[i]){
            for(int j=2*i;j<n;j+=i)
            {
                if(prime[i]){
                    prime[j]=false;
                    --count;
                }
            }
        }
    }
    return count;
}

利用质数的一些性质，我们可以进一步优化该算法

int countPrimes(int n)
{
    if(n<=2) return 0;
    vector<bool>prime(n,true);
    int i=3,sqrtn=sqrt(n),count=n/2;//偶数一定不是质数
    while(i<=sqrtn)//最小质因子一定小于等于开方数
    {
        for(int j=i*i;j<n;j+=2*i)//避免偶数和重复遍历
        {
            if(prime[j])
            {
                --count;
                prime[j]=false;
            }
        }
        do{
            i+=2;
        }while(i<=sqrtn&&!prime[i]);//避免偶数和重复遍历
    }
    return count;
}           

3.数字处理

进制转换类型的题，通常是利用除法和取模（mod）来进行计算，同时也要注意一些细节，如负数和零。如果输出是数字类型而非字符串，则也需要考虑是否会超出整数上下界。

string convertToBase7(int num)
{
    if(num==0) return "0";
    bool is_negative=num<0;
    if(is_negative) num= -num;
    string ans;
    while(num)
    {
        int a=num/7,b=num%7;
        ans=to_string(b)+ans;
        num=a;
    }
    return is_negative ? "-" + ans: ans;
}

题目一：
给定一个非负整数，判断它的阶乘结果的结尾有几个零。

每个尾部的 0 由 2 × 5 = 10 而来，因此我们可以把阶乘的每一个元素拆成质数相乘，统计有多少个 2
和 5。明显的，质因子 2 的数量远多于质因子 5 的数量，因此我们可以只统计阶乘结果里有多少个质
因子5。

int trailingZeros(int n)
{
    return n==0 ? 0:n/5+trailingZeros(n/5);
}

题目二：给定两个由数字组成的字符串，求他们相加的结果

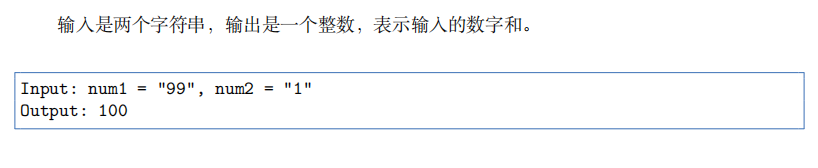
因为相加运算是从后往前进行的，所以可以先翻转字符串，再逐位计算。这种类型的题考察的是细节，如进位、位数差等等。

string addStrings(string num1,string num2)
{
    string output("");
    reverse(num1.begin(),num1.end());
    reverse(num2.begin(),num2.end());
    int onelen=num1.length(),twolen=num2.length();
    if(onelen<=twolen)
    {
         swap(num1,num2);
         swap(onelen,twolen);
     }
     int addbit;
     for(int i=0;i<twolen;++i)
     {
         int cur_sum=(num1[i]-'0')+(num2[i]-'0')+addbit;
         output+=tot_string((cur_sum)%10);
         addbit=cur_sum<10?0:1;
     }
     for(int i=twolen;i<onelen;++i)
     {
         int cur_sum=(num1[i]-'0')+addbit;
         output+=to_string((cur_sum)%10);
         addbit=cur_sum<10?0:1;
     }
     if(addbit)
     {
         output+="1";
     }
     reverse(output.begin(),output.end());
     return output;
 }

题目三：判断一个数字是否是3的次方

有两种方法，一种是利用对数。设 log3n = m，如果 n 是 3 的整数次方，那么 m 一定是整数。

bool isPowerOfThree(int n){
    return fmod(log10(n)/log10(3),1)==0;
}

另一种方法是，因为在 int 范围内 3 的最大次方是 319 = 1162261467，如果 n 是 3 的整数次方，那么 1162261467 除以 n 的余数一定是零；反之亦然。

bool isPowerOfThree(int n)
{
    return n>0&&1162261467%n==0;
}

4.随机与取样

给定一个数组，要求实现两个指令函数。第一个函数“shuffle”可以随机打乱这个数组，第二个函数“reset”可以恢复原来的顺序。

我们采用经典的 Fisher-Yates 洗牌算法，原理是通过随机交换位置来实现随机打乱，有正向和反向两种写法，且实现非常方便。注意这里“reset”函数以及类的构造函数的实现细节。

class Solution{
    vector<int>origin;
public:
    Solution(vector<int>nums):origin(std::move(nums)){}

    vector<int>reset(){
        return origin;
    }
    
    vector<int>shuffled(){
        if(origin.empty()) return {};
        vector<int>shuffled(origin);
        int n=origin.size();
        //可以使用反向或者正向洗牌，效果相同
        //反向洗牌：
        for(int i=n-1;i>=0;--i)
        {
            swap(shuffles[i],shuffled[rand()%(i+1)]);
        }
        //正向洗牌
        //for(int i=0;i<n;++i){
        //    int pos=rand()%(n-i);
        //    swap(shuffled[i],shuffled[i+pos]);
        //}
        return shuffled;
    }
};  

题目一：
给定一个数组，数组每个位置表示该位置的权重，要求按照权重的概率去随机采样

输入是一维正整数数组，表示权重；和一个包含指令字符串的一维数组，表示运行几次随机采样。输出是一维整数数组，表示随机采样的整数在数组中的位置。

我们可以先使用 partial_sum 求前缀和（即到每个位置为止之前所有数字的和），这个结果对于正整数数组是单调递增的。每当需要采样时，我们可以先随机产生一个数字，然后使用二分法查找其在前缀和中的位置，以模拟加权采样的过程。这里的二分法可以用 lower_bound 实现。以样例为例，权重数组[1,3]的前缀和为[1,4]。如果我们随机生成的数字为1，那么 lower_bound返回的位置为 0；如果我们随机生成的数字是 2、3、4，那么 lower_bound 返回的位置为 1。

class Solution{
    vector<int>sums;
public:
    Solution(vector<int>weights):sums(std::move(weights)){
        partial_sum(sums.begin(),sums.end(),sums.begin());
    }
    int pickIndex(){
        int pos=(rand()%sums.back())+1;
        return lower_bound(sums.begin(),sums.end(),pos)-sums.begin();
    }
};

题目二：
给定一个单向链表，要求设计一个算法，可以随机取得其中的一个数字。

不同于数组，在未遍历完链表前，我们无法知道链表的总长度。这里我们就可以使用水库采样：遍历一次链表，在遍历到第 m 个节点时，有 1m 的概率选择这个节点覆盖掉之前的节点选择。

class Solution{
    ListNode*head;
public:
    Solution(ListNode*n):head(n){}
    int getRandom(){
        int ans=head->val;
        ListNode*node=head-<next;
        int i=2;
        while(node){
            if((rand()%i)==0){
                ans=node->val;
            }
            ++i;
            node=node->next;
        }
        return ans;
    }
}