提供了编程的基础技术教程

zl程序教程

您现在的位置是：首页 >  工具

当前栏目

二项分布与泊松分布学习[转载]

学习 转载 分布
2023-09-14 09:11:23 时间

转自：https://blog.csdn.net/ccnt_2012/article/details/81114920

https://wenku.baidu.com/view/570c4d387375a417866f8f55.html

https://wenku.baidu.com/view/eb143a046c85ec3a87c2c52a.html

 1.泊松分布的概念

//对于Π很小，n趋近于无穷大时，为什么可以看成是二项分布的极限形式呢？在接下来，推导其公式时，会有一个将p=μ/n，的公式。

2.公式

3.从二项推导泊松

 

从图中看，每个时间段，有卖出3个的，有卖出2个的，有卖出1个的，就不再是单纯的“卖出、没卖出”了。不能套用二项分布了。

解决这个问题也很简单，把 T 分为20个时间段，那么每个时间段就又变为了抛硬币：

这样，T 内卖出7个馒头的概率就是（相当于抛了20次硬币，出现7次正面）：

\binom{20}{7}p^7(1-p)^{13}\\

为了保证在一个时间段内只会发生“卖出、没卖出”，干脆把时间切成 n 份：

\binom{n}{7}p^7(1-p)^{n-7}\\

越细越好，用极限来表示：

\lim_{n\to\infty}\binom{n}{7}p^7(1-p)^{n-7}\\

更抽象一点，T 时刻内卖出 k 个馒头的概率为：

\lim_{n\to\infty}\binom{n}{k}p^k(1-p)^{n-k}\\

“那么”，老板用笔敲了敲桌子，“只剩下一个问题，概率 p 怎么求？”

在上面的假设下，问题已经被转为了二项分布。二项分布的期望为：

E(X)=np=\mu\\

那么：

p=\frac{\mu}{n}\\

有了 p=\frac{\mu}{n}了之后，就有：

\lim_{n\to\infty}\binom{n}{k}p^k(1-p)^{n-k}=\lim_{n\to\infty}\binom{n}{k}\left(\frac{\mu}{n}\right)^k(1-\frac{\mu}{n})^{n-k}\\

我们来算一下这个极限：

\begin{align}\lim_{n\to\infty}\binom{n}{k}\left(\frac{\mu}{n}\right)^k(1-\frac{\mu}{n})^{n-k}&= \lim_{n\to\infty}\frac{n(n-1)(n-2)\cdots(n-k+1)}{k!}\frac{\mu^k}{n^k}\left(1-\frac{\mu}{n}\right)^{n-k}\\ &=\lim_{n\to\infty}\frac{\mu^k}{k!}\frac{n}{n}\cdot\frac{n-1}{n}\cdots\frac{n-k+1}{n}\left(1-\frac{\mu}{n}\right)^{-k}\left(1-\frac{\mu}{n}\right)^n\end{align}\\

其中：

\lim_{n\to\infty}\frac{n}{n}\cdot\frac{n-1}{n}\cdots\frac{n-k+1}{n}\left(1-\frac{\mu}{n}\right)^{-k}=1\\

 //这里的化简确实是思路比较那啥，我是想不出来的。

\lim_{n \to \infty}\left(1-\frac{\mu}{n}\right)^n = e^{-\mu}\\

所以：

\lim_{n\to\infty}\binom{n}{k}\left(\frac{\mu}{n}\right)^k(1-\frac{\mu}{n})^{n-k}=\frac{\mu^k}{k!}e^{-\mu}\\

上面就是泊松分布的概率密度函数，也就是说，在 T 时间内卖出 k 个馒头的概率为：

P(X=k)=\frac{\mu^k}{k!}e^{-\mu}\\

一般来说，令 \mu=\lambda ，所以：

P(X=k)=\frac{\lambda^k}{k!}e^{-\lambda}\\

//这里lamda也就是μ，也就是均值了！

对于这里的馒头的问题，一周卖出馒头的均值为：

计算样本均值：

\overline{X}=5\\

可以用它来近似：

\overline{X}\approx\mu\\

即可得到针对本题的泊松分布：

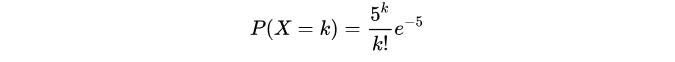
如果每天准备8个馒头的话，那么足够卖的概率就是把前8个的概率加起来，即K=8：

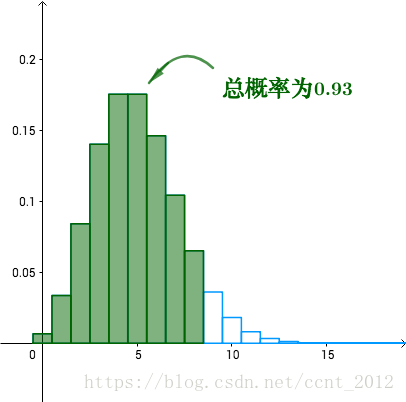
对于93%的情况是不缺货的。

4.二项与泊松

鉴于二项分布与泊松分布的关系，可以很自然的得到一个推论，当二项分布的 p 很小的时候（n很大时，那么就是使用泊松分布了），两者比较接近：

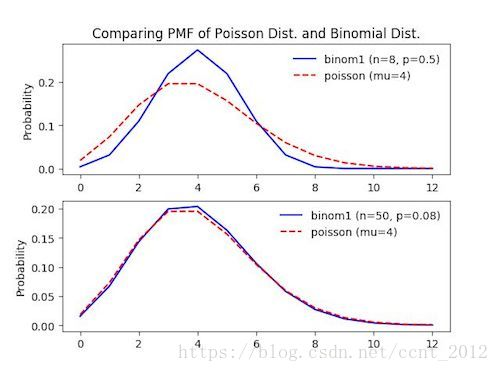
//图1中，当p较大时0.5，与泊松分布差异较大；对于图2，当p为0.08时，n也较大时，和泊松分布差异较小。

5.泊松分布的性值 

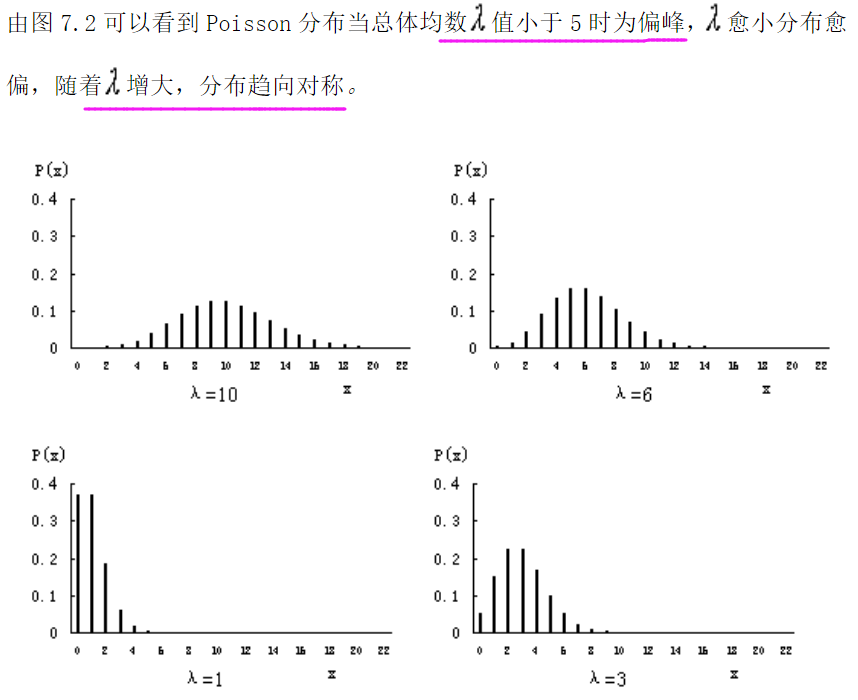
6.泊松分布的期望与方差

6.1期望

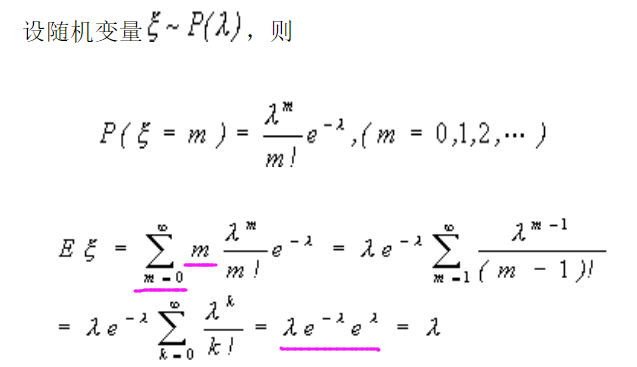
6.2方差

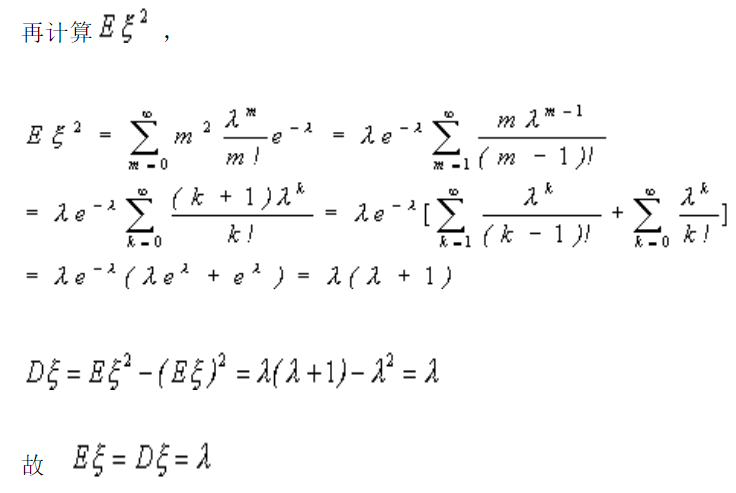
7.二项分布期望及方差证明

7.1常规证明期望

//感觉这个推导还是挺难的，让我手写我写不出来。目的就是把k给化掉。其中倒数第三个等号到倒数第二个等号之间的转换没有看懂。

7.2常规证明方差

就不放了，反正也看懂，就是D(X)=E(X^2)-(E(X))^2

7.3和的期望=期望的和

7.4独立变量的和的方差=方差的和

//这里不太明白为什么单个的方差=θ(θ-1).

相关文章