图匹配学习
图匹配
对于一个给定的图
G
=
(
V
,
E
)
G = \left(V, E\right)
G=(V,E),
V
V
V是点集,
E
E
E是边集
一组两两不相邻(没有公共顶点)的边集
M
⊆
E
M\subseteq E
M⊆E称为这张图的匹配(matching)
如果一个顶点是匹配中的边的顶点,则称这个顶点是被匹配的/匹配点(饱和的, matched, saturated)
匹配中的边称为匹配边,反之称为未匹配边
定义匹配的大小为边的数量
∣
M
∣
\left|M\right|
∣M∣
极大匹配(maximal matching):匹配
M
M
M不是
G
G
G任何其他匹配的真子集,换句话说不能再往匹配中加匹配边,如下图
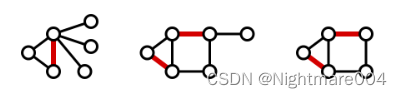
最大匹配(maximum matching):边数最多的匹配,如下图

最大匹配中匹配点的数量称为图的配对数(matching number),记作
ν
(
G
)
\nu\left(G\right)
ν(G)
当图中的边带权的时候,边权和最大的为最大权匹配
完美匹配(Perfect Match):一个包括图中所有顶点的匹配,是最大匹配的一种
近似完美匹配/准完美匹配(near-perfect matching):只有一个点不是匹配点,扣掉此点以后的图称为 factor-critical graph
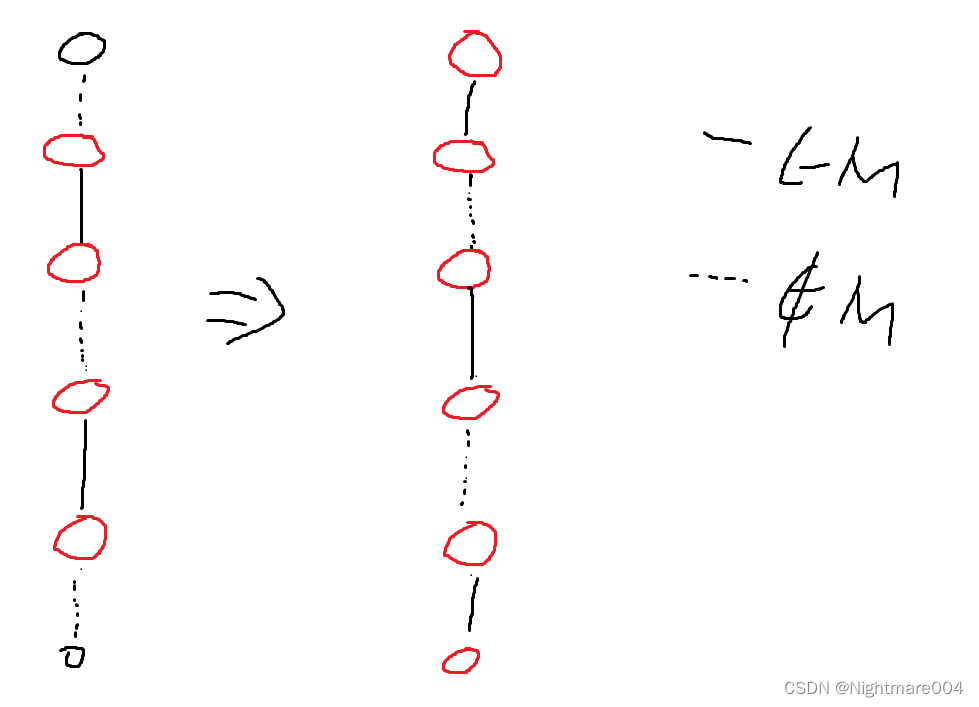
交错路(alternating path) :始于非匹配点且由匹配边与非匹配边交错而成
增广路(augmenting path):始于非匹配点且终于非匹配点的交错路
增广路定理
增广路定理(Berge’s lemma):图
G
G
G的匹配
M
M
M是最大匹配,当且仅当不存在增广路
交错路(alternating path) :始于非匹配点且由匹配边与非匹配边交错而成
增广路(augmenting path):始于非匹配点且终于非匹配点的交错路
证明:
必要性:假设
M
M
M是最大匹配
假设存在增广路
因为增广路中,未匹配边比匹配边多1(可以自己画个图感受一下)
将增广路中,匹配边改为未匹配边,未匹配边改为匹配边,则匹配数增加1,与最大匹配矛盾
充分性:假设不存在增广路
假设存在更大的匹配
M
′
M^{\prime}
M′
令
D
D
D为
(
M
−
M
′
)
∪
(
M
′
−
M
)
\left(M - M^{\prime}\right)\cup\left(M' - M\right)
(M−M′)∪(M′−M)
则
D
D
D中的顶点有3中情况:
1.孤立点
2.由
M
M
M和
M
′
M^{\prime}
M′中的边交替组成的长度为偶数的环
3.由
M
M
M和
M
′
M^{\prime}
M′中的边交替组成的两个端点不同的路径
(因为
D
D
D不会出现度为大于等于3的顶点,所以只能出现孤立点、环和路径;
由图匹配,路径中不会出现连续两条边属于同一个匹配,所以必然是交替的;
不会出现长度为奇数的环(画个图就知道为啥了))
由于
M
′
M^{\prime}
M′是更大的匹配,所以
D
D
D中一定是存在边的,并且一定存在属于
M
′
M^{\prime}
M′的边
于是存在增广路(比如偶数环/长度为奇数的路径/偶数的路径砍一条边的奇数路径)
于是矛盾
增广路算法
根据增广路定理,我们只需要
枚举未匹配点,找增广路径,将增广路上的非匹配边变为匹配边,匹配边变为非匹配边,就能找到最大匹配
这里注意,每个顶点只需要枚举一次
因为我们每一次是找增广路,将非匹配边变为匹配边,匹配边变为非匹配边,结果是,只有两个端点由非匹配点变为匹配点,其他点是不会受到影响
二分图
二分图(bipartite graph)又称为二部图、偶图、双分图。
二分图的顶点可以分成两个互斥的独立集
U
U
U和
V
V
V的图,使得所有边都是连接一个
U
U
U中的点和
V
V
V中的点
等价的,二分图可以被定义称图中的环都有偶数个顶点
二分图一种描述方式为
G
=
(
U
,
V
,
E
)
G = \left(U,V,E\right)
G=(U,V,E)
二分图匹配
一张二分图上的匹配称为二分匹配
完美匹配:设
G
=
(
V
1
,
V
2
,
E
)
,
∣
V
1
∣
≤
∣
V
2
∣
G = \left(V_1, V_2, E\right),\left|V_1\right| \le \left|V_2\right|
G=(V1,V2,E),∣V1∣≤∣V2∣
M
M
M为
G
G
G中一个最大匹配,且
∣
M
∣
=
∣
V
1
∣
\left|M\right| = \left|V_1\right|
∣M∣=∣V1∣,则称
M
M
M为
V
1
V_1
V1到
V
2
V_2
V2的完美匹配
Hall’s Marriage Theorem
霍尔定理/霍尔婚配定理(Hall’s Marriage Theorem):设二分图 G = ( V 1 , V 2 , E ) , ∣ V 1 ∣ ≤ ∣ V 2 ∣ G = \left(V_1, V_2, E\right),\left|V_1\right| \le \left|V_2\right| G=(V1,V2,E),∣V1∣≤∣V2∣,则 G G G中存在 V 1 V_1 V1到 V 2 V_2 V2的完美匹配当且仅当对于任意的 S ⊂ V 1 S\subset V_1 S⊂V1,均有 ∣ S ∣ ≤ ∣ N ( S ) ∣ \left|S\right|\le\left|N\left(S\right)\right| ∣S∣≤∣N(S)∣
其中 N ( v ) N\left(v\right) N(v)表示 v v v相邻的顶点, N ( S ) = ∪ v i ∈ S N ( V i ) N\left(S\right) = \cup_{v_i\in S}N\left(V_i\right) N(S)=∪vi∈SN(Vi)
证明:
必要性:显然
充分性:假设对于任意的
S
⊂
V
1
S\subset V_1
S⊂V1,均有
∣
S
∣
≤
∣
N
(
S
)
∣
\left|S\right|\le\left|N\left(S\right)\right|
∣S∣≤∣N(S)∣
当
∣
V
1
∣
=
1
\left|V_1\right| =1
∣V1∣=1时,显然成立
假设
∣
V
1
∣
<
n
\left|V_1\right| < n
∣V1∣<n时都成立
当 ∣ V 1 ∣ = n \left|V_1\right| = n ∣V1∣=n时
如果对于任意的满足
∣
S
∣
=
k
\left|S\right| = k
∣S∣=k的集合
S
S
S,都有
∣
N
(
S
)
∣
≤
k
+
1
\left|N\left(S\right)\right| \le k +1
∣N(S)∣≤k+1
不妨假设
u
∈
V
1
,
w
∈
V
2
u \in V_1,\ w \in V_2
u∈V1, w∈V2,
G
′
=
(
V
1
−
{
u
}
,
V
2
−
{
w
}
,
E
−
{
(
u
,
w
)
}
)
G^{\prime}=\left(V_1 - \left\{u\right\},V_2 - \left\{w\right\},E-\left\{(u,w)\right\}\right)
G′=(V1−{u},V2−{w},E−{(u,w)})
则根据归纳,
G
′
G^{\prime}
G′是一个二分图,进而
G
G
G也是二分图
如果存在
S
S
S,满足
∣
S
∣
=
∣
N
(
S
)
∣
=
k
\left|S\right| = \left|N\left(S\right)\right| = k
∣S∣=∣N(S)∣=k
则
G
′
=
(
S
,
N
(
S
)
)
G^{\prime} = \left(S,N\left(S\right)\right)
G′=(S,N(S))是一个二分图,
G
′
′
=
(
V
1
−
S
,
V
2
−
N
(
S
)
)
G^{\prime\prime} = \left(V_1 - S,V_2 - N\left(S\right)\right)
G′′=(V1−S,V2−N(S))也是,拼一起,
G
G
G也是二分图
Kőnig’s theorem
在任意二分图中,最大匹配的边数等于最小顶点覆盖的顶点数
图的顶点覆盖是指它的一个顶点集,该图的每一条边都至少有一个端点在这个顶点集中。如果该图没有一个点数更少的顶点覆盖,则称其为最小顶点覆盖
证明:
设最小定点覆盖为
C
C
C,最大匹配为
M
M
M
显然
∣
C
∣
≥
∣
M
∣
\left|C\right| \ge \left|M\right|
∣C∣≥∣M∣
设二分图为
G
=
(
V
1
,
V
2
,
E
)
G = \left(V_1, V_2, E\right)
G=(V1,V2,E)
取顶点集
C
C
C如下:对于
M
M
M的每条边,如果存在交错路终止于该边在
V
2
V_2
V2中的端点,那么该端点属于
C
C
C,否则该边在
V
1
V_1
V1中的端点属于
C
C
C
显然
∣
C
∣
=
∣
M
∣
\left|C\right| = \left|M\right|
∣C∣=∣M∣
对于任意
v
1
∈
V
1
,
v
2
∈
V
2
,
(
v
1
,
v
2
)
∈
E
v_1 \in V_1,v_2 \in V_2,\left(v_1,v_2\right) \in E
v1∈V1,v2∈V2,(v1,v2)∈E
如果
(
v
1
,
v
2
)
∈
M
\left(v_1,v_2\right) \in M
(v1,v2)∈M,则必然被覆盖
如果
(
v
1
,
v
2
)
∉
M
\left(v_1,v_2\right) \not\in M
(v1,v2)∈M
如果
v
1
v_1
v1不是匹配点,则
v
1
v
2
v_1v_2
v1v2是交错路,则
v
2
∈
C
v_2 \in C
v2∈C,
(
v
1
,
v
2
)
\left(v_1,v_2\right)
(v1,v2)被覆盖
如果
v
1
v_1
v1是匹配点,则
v
2
v_2
v2不是匹配点(不然与
(
v
1
,
v
2
)
∉
M
\left(v_1,v_2\right) \not\in M
(v1,v2)∈M矛盾)
那么必然存在
v
1
′
v
2
′
v
1
v
2
v_1^{\prime}v_2^{\prime}v_1 v_2
v1′v2′v1v2,其中
v
2
′
v_2^{\prime}
v2′是匹配点,
v
1
′
v_1^{\prime}
v1′不是匹配点(因为不可能两个匹配点连着),进而
v
1
∈
C
v_1 \in C
v1∈C,
(
v
1
,
v
2
)
\left(v_1,v_2\right)
(v1,v2)被覆盖
综上所述,每条边都被覆盖了
增广路算法
增广路算法(Augmenting Path Algorithm)
枚举未匹配点(每个点只要枚举一次),找增广路,未匹配边和匹配边互换,匹配数+1
时间复杂度
O
(
∣
V
∣
∣
E
∣
)
O\left(\left|V\right| \left|E\right|\right)
O(∣V∣∣E∣)
洛谷P3386
#include<cstdio>
#include<cstring>
#include<vector>
using namespace std;
const int N = 505;
const int M = 505;
int n;//V1的顶点数
int m;//V2的顶点数
vector<int> edge[N];//二分图(V1,V2,E)中V1的边
bool visit[M];//V2中的点是否访问过
int pb[M];//V2->V1的匹配
int res;//匹配数
bool dfs(int u) {
for (int i = 0; i < edge[u].size(); ++i) {
int v = edge[u][i];
if (visit[v])continue;
visit[v] = true;
//u(未匹配)->v(未匹配)
//u(未匹配)->v---(匹配)--->pb[v]->(从pb[v]找增广路
if (pb[v] == -1 || dfs(pb[v])) {
pb[v] = u;
return true;
}
}
return false;
}
void solve() {
res = 0;
memset(pb, -1, sizeof(pb));
for (int i = 1; i <= n; ++i) {
memset(visit, false, sizeof(visit));
if (dfs(i)) {//找到增广路
++res;
}
}
}
int main() {
int e, u, v;
scanf("%d%d%d", &n, &m, &e);
while (e--) {
scanf("%d%d", &u, &v);
edge[u].push_back(v);
}
solve();
printf("%d\n", res);
return 0;
}
时间戳的(不用每次memset
#include<cstdio>
#include<cstring>
#include<vector>
using namespace std;
const int N = 505;
const int M = 505;
int n;//V1的顶点数
int m;//V2的顶点数
vector<int> edge[N];//二分图(V1,V2,E)中V1的边
int visit[M];//V2中的点时间戳
int dfsn;//时间戳
int pb[M];//V2->V1的匹配
int res;//匹配数
bool dfs(int u) {
for (int i = 0; i < edge[u].size(); ++i) {
int v = edge[u][i];
if (visit[v] == dfsn)continue;
visit[v] = dfsn;
//u(未匹配)->v(未匹配)
//u(未匹配)->v---(匹配)--->pb[v]->(从pb[v]找增广路
if (pb[v] == -1 || dfs(pb[v])) {
pb[v] = u;
return true;
}
}
return false;
}
void solve() {
res = 0;
memset(visit, 0, sizeof(visit));
memset(pb, -1, sizeof(pb));
for (int i = 1; i <= n; ++i) {
++dfsn;
if (dfs(i)) {//找到增广路
++res;
}
}
}
int main() {
int e, u, v;
scanf("%d%d%d", &n, &m, &e);
while (e--) {
scanf("%d%d", &u, &v);
edge[u].push_back(v);
}
solve();
printf("%d\n", res);
return 0;
}
bfs
相当于多路增广
#include<cstdio>
#include<cstring>
#include<vector>
#include<queue>
using namespace std;
const int N = 505;
const int M = 505;
int n;//V1的顶点数
int m;//V2的顶点数
vector<int> edge[N];//二分图(V1,V2,E)中V1的边
int visit[M];//V2中的点时间戳
int dfsn;//时间戳
int pre[N];//V1前驱(队列里)
int pa[N];//V1->V2的匹配
int pb[M];//V2->V1的匹配
int res;//匹配数
void solve() {
res = 0;
memset(pa, -1, sizeof(pa));
memset(pb, -1, sizeof(pb));
memset(visit, 0, sizeof(visit));
for (int i = 1; i <= n; ++i) {
if (pa[i] != -1)continue;//匹配点
queue<int> q;
q.push(i);
pre[i] = -1;
bool flag = false;//是否找到增广路
while (!q.empty() && !flag) {
int u = q.front();
q.pop();
for (int j = 0; j < edge[u].size(); ++j) {
int v = edge[u][j];
//访问过了
if (visit[v] == i)continue;
visit[v] = i;
if (pb[v] != -1) {//u->v--匹配过-->pb[v]
q.push(pb[v]);
pre[pb[v]] = u;
}
else {//找到增广路 ...->u->v(未匹配)
flag = true;
//增广路的匹配边与未匹配边互换
while (u != -1) {
int temp = pa[u];
pa[u] = v;
pb[v] = u;
u = pre[u];
v = temp;
}
break;
}
}
}
//找到了增广路
if (flag) {
++res;
}
}
}
int main() {
int e, u, v;
scanf("%d%d%d", &n, &m, &e);
while (e--) {
scanf("%d%d", &u, &v);
edge[u].push_back(v);
}
solve();
printf("%d\n", res);
return 0;
}
Hopcroft–Karp algorithm
霍普克洛夫特-卡普算法(Hopcroft–Karp algorithm,Hopcroft–Karp–Karzanov algorithm)
时间复杂度
O
(
∣
V
∣
∣
E
∣
)
O\left(\sqrt{\left|V\right|}\left|E\right|\right)
O(∣V∣∣E∣)
算法流程

首先用bfs找到最短的增广路集合,如果找不到,就结束
然后用dfs增广
重复这两步
#include<cstdio>
#include<cstring>
#include<vector>
#include<queue>
using namespace std;
const int N = 505;
const int M = 505;
const int INF = 0x3f3f3f3f;
int n;//V1的顶点数
int m;//V2的顶点数
vector<int> edge[N];//二分图(V1,V2,E)中V1的边
int visit[M];//V2中的点时间戳
int dfsn;//时间戳
int pre[N];//V1前驱(队列里)
int pa[N];//V1->V2的匹配
int pb[M];//V2->V1的匹配
int da[N];//V1中的顶点在bfs搜索树的层
int db[M];//V2中的顶点在bfs搜索树的层
int res;//匹配数
int dis;//最短增广路长度
bool bfs() {
queue<int> q;
dis = INF;
memset(da, -1, sizeof(da));
memset(db, -1, sizeof(da));
for (int i = 1; i <= n; ++i) {
if (pa[i] == -1) {//找未匹配点
q.push(i);
da[i] = 0;
}
}
while (!q.empty()) {
int u = q.front();
q.pop();
if (da[u] > dis)break;//不是最短增广路
for (int i = 0; i < edge[u].size(); ++i) {
int v = edge[u][i];
if (db[v] == -1) {//没访问过
db[v] = da[u] + 1;
if (pb[v] == -1) {//未匹配,说明找到了增广路
dis = db[v];
}
else {//u->v->pb[v]
da[pb[v]] = db[v] + 1;
q.push(pb[v]);
}
}
}
}
return dis != INF;
}
bool dfs(int u) {
for (int i = 0; i < edge[u].size(); ++i) {
int v = edge[u][i];
if (visit[v] != dfsn && db[v] == da[u] + 1) {
visit[v] = dfsn;
if (pb[v] != -1 && db[v] == dis)continue;//这条路已经被找过了
if (pb[v] == -1 || dfs(pb[v])) {
pb[v] = u;
pa[u] = v;
return true;
}
}
}
return false;
}
void Hopcroft_Karp() {
memset(pa, -1, sizeof(pa));
memset(pb, -1, sizeof(pb));
while (bfs()) {//有增广路
++dfsn;
for (int i = 1; i <= n; ++i) {
if (pa[i] == -1 && dfs(i)) {//感觉写da[i] == 0 && dfs(i)也可以
++res;
}
}
}
}
int main() {
int e, u, v;
scanf("%d%d%d", &n, &m, &e);
while (e--) {
scanf("%d%d", &u, &v);
edge[u].push_back(v);
}
Hopcroft_Karp();
printf("%d\n", res);
return 0;
}
二分图最大权匹配
二分图的最大权匹配是指二分图中边权和最大的匹配
匈牙利算法
匈牙利算法(Hungarian algorithm,Kuhn–Munkres algorithm,Munkres assignment algorithm)
Harold Kuhn基于两个匈牙利数学家Harold Kuhn和Jenő Egerváry的工作提出了这个算法,命名为Hungarian method
匈牙利算法用来解决二分图的最大权完美匹配,时间复杂度 O ( ∣ V ∣ 3 ) O\left(\left|V\right|^3\right) O(∣V∣3)
首先由两个概念
可行顶标:给每个顶点
i
i
i分配一个权值
l
(
i
)
l\left(i\right)
l(i),对于所有边
(
u
,
v
)
\left(u,v\right)
(u,v)满足
w
(
u
,
v
)
≤
l
(
u
)
+
l
(
v
)
w\left(u,v\right) \le l\left(u\right) + l\left(v\right)
w(u,v)≤l(u)+l(v)
紧边:满足
l
(
u
)
+
l
(
v
)
=
w
(
u
,
v
)
l\left(u\right) + l\left(v\right) = w\left(u,v\right)
l(u)+l(v)=w(u,v)的边
(
u
,
v
)
\left(u,v\right)
(u,v)
相等子图:在一组可行顶标下原图的生成子图,包含所有点但只包含满足
w
(
u
,
v
)
=
l
(
u
)
+
l
(
v
)
w\left(u,v\right) = l\left(u\right) + l\left(v\right)
w(u,v)=l(u)+l(v)的边
(
u
,
v
)
\left(u,v\right)
(u,v)
定理1:对于满足可行定标,如果其相等子图存在完美匹配,那么,该匹配就是原二分图的最大全完美匹配
有了定理1,我们的目标就是调整可行顶标,使得相等子图是完美匹配
首先初始化一组可行顶标,比如
l
a
(
i
)
=
max
1
≤
j
≤
n
{
w
(
i
,
j
)
}
,
l
b
(
i
)
=
0
la\left(i\right) = \max_{1\le j \le n}\left\{w\left(i,j\right)\right\}, lb(i) = 0
la(i)=max1≤j≤n{w(i,j)},lb(i)=0
(左边是出边权值最大,右边是0)
然后选一个未匹配点,沿着紧边找增广路(比如增广路算法),找到了就增广,否则会得到交错树(就是搜索过的顶点组成的树)
设
S
,
T
S,T
S,T是左右两边在交错树的顶点,
S
′
,
T
′
S^\prime, T^\prime
S′,T′表示不再交错树的顶点
在相等子图中:
S
−
T
′
S-T^\prime
S−T′的边不存在,否则交错树会增长
S
′
−
T
S^\prime-T
S′−T一定是非匹配边,否则应该在
S
S
S里
假设给
S
S
S中的顶标
−
a
-a
−a,给
T
T
T中的定标
+
a
+a
+a,可以发现
S
−
T
S-T
S−T边依然存在相等子图中(因为抵消了)
S
′
−
T
′
S^\prime-T^\prime
S′−T′没变化
S
−
T
′
S-T^\prime
S−T′中
l
a
+
l
b
la + lb
la+lb有所减少,可能加入相等子图
S
′
−
T
S^\prime -T
S′−T中的
l
a
+
l
b
la+lb
la+lb增加,不会加入相等子图
当
a
a
a也不能乱取,得保证
l
a
(
u
)
+
l
b
(
v
)
−
w
(
u
,
v
)
≥
0
la\left(u\right) + lb\left(v\right) - w\left(u,v\right) \ge 0
la(u)+lb(v)−w(u,v)≥0
所以
a
=
min
{
l
a
(
u
)
+
l
b
(
v
)
−
w
(
u
,
v
)
∣
u
∈
S
,
v
∈
T
′
}
a = \min\left\{la\left(u\right) + lb\left(v\right) - w\left(u,v\right)|u\in S, v\in T^\prime\right\}
a=min{la(u)+lb(v)−w(u,v)∣u∈S,v∈T′}
至多经过
n
n
n次修改顶标后,就可以找到增广路
每次修改顶标的时候,交错树种的边不会离开相等子图,那么我们直接维护这棵树
s
l
a
c
k
(
v
)
=
min
{
l
a
(
u
)
+
l
b
(
v
)
−
w
(
u
,
v
)
∣
u
∈
S
}
slack(v) = \min\left\{la\left(u\right) + lb\left(v\right) - w\left(u,v\right)|u\in S\right\}
slack(v)=min{la(u)+lb(v)−w(u,v)∣u∈S}
这样
a
a
a就可以在
O
(
n
)
O\left(n\right)
O(n)的时间求出来
最后时间复杂度
O
(
n
3
)
O\left(n^3\right)
O(n3)
代码
洛谷P6577
dfs
dfs,然而这种会T
#include<cstdio>
#include<cstring>
#include<algorithm>
typedef long long LL;
const int N = 505;
int n;
LL edge[N][N];//二分图边
LL slack[N];//V2的松弛 slack[j] = min{la(i) + la(j) - w(i,j)| forall i}
bool visit_a[N];//访问V1
bool visit_b[N];//访问V2
int pb[N];//V2->V1的匹配
LL la[N];//V1顶标
LL lb[N];//V2顶标
bool dfs(int u) {
visit_a[u] = true;
for (int v = 1; v <= n; ++v) {
if (visit_b[v])continue;
LL delta = la[u] + lb[v] - edge[u][v];
if (delta == 0) {//只走紧边
visit_b[v] = true;
if (pb[v] == -1 || dfs(pb[v])) {
pb[v] = u;
return true;
}
}
else {
slack[v] = std::min(slack[v], delta);
}
}
return false;
}
void Kuhn_Munkres() {
memset(pa, -1, sizeof(pa));
memset(pb, -1, sizeof(pb));
memset(lb, 0, sizeof(lb));
for (int i = 1; i <= n; ++i) {
la[i] = edge[i][1];
for (int j = 2; j <= n; ++j) {
la[i] = std::max(la[i], edge[i][j]);
}
}
for (int i = 1; i <= n; ++i) {
memset(slack, 0x3f, sizeof(slack));//inf
while (true) {
memset(visit_a, false, sizeof(visit_a));
memset(visit_b, false, sizeof(visit_b));
if (dfs(i))break;
//未访问最小松弛量
LL d = 0x3f3f3f3f3f3f3f3f;
for (int j = 1; j <= n; ++j) {
if (!visit_b[j]) {
d = std::min(d, slack[j]);
}
}
//松弛
for (int j = 1; j <= n; ++j) {
if (visit_a[j]) {//交错树中V1的点-d
la[j] -= d;
}
if (visit_b[j]) {//交错树中V2的点+d
lb[j] += d;
}
else {//交错树外V2的点slack -d
slack[j] -= d;
}
}
}
}
LL res = 0;
for (int v = 1; v <= n; ++v) {
res += la[pb[v]] + lb[v];
}
printf("%lld\n", res);
for (int v = 1; v <= n; ++v) {
if (v > 1)printf(" ");
printf("%d", pb[v]);
}
printf("\n");
}
int main() {
int m, y, c;
LL h;
memset(edge, 0xc0, sizeof(edge));//-inf
scanf("%d%d", &n, &m);
for (int i = 0; i < m; ++i) {
scanf("%d%d%lld", &y, &c, &h);
edge[y][c] = h;
}
Kuhn_Munkres();
return 0;
}
bfs
在每次扩大子图后,都记录一下新加入的相等边所为我们提供的新増广方向,然后从此处继续寻找増广路即可
#include<cstdio>
#include<cstring>
#include<queue>
#include<algorithm>
typedef long long LL;
const int N = 505;
int n;
LL edge[N][N];//二分图边
LL slack[N];//V2的松弛 slack[j] = min{la(i) + la(j) - w(i,j)| forall i}
bool visit_a[N];//访问V1
bool visit_b[N];//访问V2
int pa[N];//V1->V2的匹配
int pb[N];//V2->V1的匹配
int pre[N];//V1前驱(队列里)
LL la[N];//V1顶标
LL lb[N];//V2顶标
std::queue<int> q;
void aug(int v) {
while (v != -1) {
//pa[pre[v]] -> v
int temp = pa[pre[v]];
pa[pre[v]] = v;
pb[v] = pre[v];
v = temp;
}
}
void bfs(int s) {
memset(visit_a, false, sizeof(visit_a));
memset(visit_b, false, sizeof(visit_b));
memset(slack, 0x3f, sizeof(slack));
while (!q.empty()) {
q.pop();
}
q.push(s);
visit_a[s] = true;
while (true) {
while (!q.empty()) {
int u = q.front();
q.pop();
for (int v = 1; v <= n; ++v) {
if (visit_b[v])continue;
LL delta = la[u] + lb[v] - edge[u][v];
if (delta <= slack[v]) {
pre[v] = u;
if (delta > 0) {
slack[v] = delta;
}
else {//紧边
visit_b[v] = true;
if (pb[v] == -1) { //未匹配,找到了增广路
aug(v);//增广
return;
}
else {
q.push(pb[v]);
visit_a[pb[v]] = true;
}
}
}
}
}
//未访问最小松弛量
LL d = 0x3f3f3f3f3f3f3f3f;
for (int v = 1; v <= n; ++v) {
if (!visit_b[v]) {
d = std::min(d, slack[v]);
}
}
//松弛
for (int i = 1; i <= n; ++i) {
if (visit_a[i]) {//交错树中V1的点-d
la[i] -= d;
}
if (visit_b[i]) {//交错树中V2的点+d
lb[i] += d;
}
else {//交错树外V2的点slack -d
slack[i] -= d;
}
}
for (int v = 1; v <= n; ++v) {
if (visit_b[v] || slack[v] != 0)continue;
visit_b[v] = true;
if (pb[v] == -1) { //未匹配,找到了增广路
aug(v);//增广
return;
}
else {
q.push(pb[v]);
visit_a[pb[v]] = true;
}
}
}
}
void Kuhn_Munkres() {
memset(pa, -1, sizeof(pa));
memset(pb, -1, sizeof(pb));
memset(lb, 0, sizeof(lb));
for (int i = 1; i <= n; ++i) {
la[i] = edge[i][1];
for (int j = 2; j <= n; ++j) {
la[i] = std::max(la[i], edge[i][j]);
}
}
for (int i = 1; i <= n; ++i) {
bfs(i);
}
LL res = 0;
for (int v = 1; v <= n; ++v) {
res += la[pb[v]] + lb[v];
}
printf("%lld\n", res);
for (int v = 1; v <= n; ++v) {
if (v > 1)printf(" ");
printf("%d", pb[v]);
}
printf("\n");
}
int main() {
int m, y, c;
LL h;
memset(edge, 0xc0, sizeof(edge));//-inf
scanf("%d%d", &n, &m);
for (int i = 0; i < m; ++i) {
scanf("%d%d%lld", &y, &c, &h);
edge[y][c] = h;
}
Kuhn_Munkres();
return 0;
}
迭代
https://blog.csdn.net/c20182030/article/details/73330556
参考:
https://en.wikipedia.org/wiki/Berge%27s_theorem
https://zhuanlan.zhihu.com/p/524349780
https://zhuanlan.zhihu.com/p/520743215

