基于精英混沌搜索策略的交替正余弦算法

摘要：正余弦算法是一种新的基于种群的随机寻优方法,利用正余弦函数使解震荡性地趋于全局最优解,其线性调整策略及较弱的局部搜索能力严重地影响了算法的性能.为了提高正弦余弦算法的计算精度,提出基于精英混沌搜索策略的交替正余弦算法.新算法采用基于对数曲线的非线性调整策略修改控制参数,利用精英个体的混沌搜索策略增强算法的开发能力,并将基于该策略的正余弦算法与反向学习算法交替执行增强算法的探索能力,降低算法的时间复杂度,提高算法的收敛速度。

1.正余弦算法

基础正余弦算法的具体原理参考，我的博客：https://blog.csdn.net/u011835903/article/details/107762654

2.改进正余弦算法

2.1 控制参数的非线性调整策略

在 SCA中, 参数 $r_1$ 起着平衡全局探索能力和局 部搜索能力的重要作用. 当 $r_1<1$ 时使下一代的解 位于当前解与目标解之间, 强调算法的开发能力; 当 $r_1>1$ 时解位于当前解和目标解之外, 强调算法的探索能力. 由式 (2) 可以看出, $r_1$ 随迭代次数的增加线性 递减, 在算法迭代初期, $r_1$ 的值较大, 使算法具有较强 的全局探索能力, 在算法迭代后期, $r_1$ 的值较小, 增加 了算法的开发能力. 但是, 线性变化方式不能有效地 增加 SCA 的寻优精度, 本文通过非线性函数 $[5]$ 对 $r_1$ 进行改进. 利用自然对数在 $[1,e]$ 上非线性递增的特 性, $r_1$ 的调整策略为
$$\begin{array}{rl}& r_1(t)=a_{\text{start }}-\left(a_{\text{start }}-a_{\text{end }}\right)\ln \left(1+\frac{(e-1)}{\eta }\cdot \frac{t}{t_{\max }}\right)\end{array}\text{\hspace{1em}(3)}$$
其中: $a_{\text{start }}、a_{\text{end }}$ 为控制参数 $a$ 的初始值和最终值, $a_{\text{start }}>a_{\mathrm{end}}⩾0;\eta >0$ 为调节系数. 由式(3)可以 看出, $r_1$ 随着迭代次数的增加非线性变化, 可以有效 地平衡 SCA 的探索和开发能力, 提高算法的寻优能 力和收敛速度.

2.2 反向学习策略

反向学习 $(\mathrm{OBL}{)}^{[6]}$ 是增强随机优化算法性能的 重要方法,通过贪婪选择目标函数在当前解和反向解 种群的适应度值, 增强了种群的多样性, 提高了算法 接近全局最优解的能力. 文献 [4] 提出的 $\mathrm{OBSCA}$ 在 基本 SCA 中加入反向学习策略, 提高了 SCA 的求解 精度. 本文旨在将 $\mathrm{SCA}$ 与反向学习策略交替进行, 以 降低算法的复杂性, 从而在改进种群多样性的同时提 高算法的收敛速度.
定义 1 反向解. 设第 $t$ 代种群中第 $i$ 个个体为 $x_i^t=\left(x_{i1}^t,x_{i2}^t,\cdots ,x_{in}^t\right)$, 记 $a_j、b_j$ 为搜索空间中第 $j$ 维的下界和上界, 令
$${\bar{x}}_{ij}^t=a_j+b_j-x_{ij}^t.\text{\hspace{1em}(4)}$$
称 ${\bar{x}}_i^t=\left({\bar{x}}_{i1}^t,{\bar{x}}_{i2}^t,\cdots ,{\bar{x}}_{in}^t\right)$ 为其反向解.
由式 (4) 可知, 反向学习算法通过反向策略产生 $N$ 个反向解,使算法在 $2N$ 个个体中挑选优秀个体进 入下一代, 增强了种群的多样性和全局探索能力, 同 时贪婪选择策略又增加了算法的收敛速度.

2.3 精英混沌搜索策略

群智能算法的优劣在于有效地平衡算法的探索 与开发能力,为了提高算法的开发能力利用混沌的 随机性、遍历性和规律性的特点, 对精英个体 ${}^{[7]}$ 进行 混沌变异. 对种群中 $N$ 个个体按适应度值升序排序, 选择前 $m=\mathrm{pr}\cdot N$ 个个体作为精英个体, $\mathrm{pr}\in [0,1]$ 为选择比例, 记精英个体为 { e x 1 t , e x 2 t , ⋯   , e x m t } ⊂ \left\{\mathrm{ex}_1^t, \mathrm{ex}_2^t, \cdots, \mathrm{ex}_m^t\right\} \subset {ex1t​,ex2t​,⋯,exmt​}⊂ { x 1 t , x 2 t , ⋯   , x N t } , ex ⁡ i t = ( ex ⁡ i 1 t , ex ⁡ i 2 t , ⋯   , e x i n t ) , i = \left\{x_1^t, x_2^t, \cdots, x_N^t\right\}, \operatorname{ex}_i^t=\left(\operatorname{ex}_{i 1}^t, \operatorname{ex}_{i 2}^t, \cdots, \mathrm{ex}_{i n}^t\right), i= {x1t​,x2t​,⋯,xNt​},exit​=(exi1t​,exi2t​,⋯,exint​),i= $1,2,\cdots ,m$. 其第 $j(j=1,2,\cdots ,n)$ 维的上下界 ${}^{[8]}$ 分 别为
$$\{\begin{array}{l}{\mathrm{eb}}_j^t=\max \left({\mathrm{ex}}_{1j}^t,{\mathrm{ex}}_{2j}^t,\cdots ,{\mathrm{ex}}_{mj}^t\right),\\ {\mathrm{ea}}_j^t=\min \left({\mathrm{ex}}_{1j}^t,{\mathrm{ex}}_{2j}^t,\cdots ,{\mathrm{ex}}_{mj}^t\right)\end{array}\text{\hspace{1em}(5)}$$
将精英个体 ${\mathrm{ex}}_i^t$ 由解空间按式 (6)映射到 $[0,1]$, 得到混 沌变量 $C_i^t=\left(C_{i1}^t,C_{i2}^t,\cdots ,C_{in}^t\right)$, 有
$$C_{ij}^t=\frac{{\mathrm{ex}}_{ij}^t-{\mathrm{ea}}_j^t}{{\mathrm{eb}}_j^t-{\mathrm{ea}}_j^t}.\text{\hspace{1em}(6)}$$
利用式 (7) 对 $C_{ij}^t$ 进行混沌迭代, 有
$$C_{ij}^t(k+1)=\mu C_{ij}^t(k)\left(1-C_{ij}^t(k)\right).\text{\hspace{1em}(7)}$$
其中: $\mu$ 为常数, 取值为 $4;k$ 为混沌迭代次数, $0⩽k⩽$ $\mathrm{ceil}(t/10),\mathrm{ceil}(x)$ 表示对 $x$ 向上取整.
当 $k$ 达到最大迭代次数 $k_{\max }$ 时, 得到第 $i$ 个精英 个体对应的混沌变量 $C_i^{k_{\max }}$, 利用下式将其映射至 $\left[{\mathrm{ea}}_j^t,{\mathrm{eb}}_j^t\right]$ 内, 得到对应混沌个体 $x{C}_i^t$, 有
$$x{C}_{ij}^t=C_{ij}^{k_{\max }}\left({\mathrm{eb}}_j^t-{\mathrm{ea}}_j^t\right)+{\mathrm{ea}}_j^t.\text{\hspace{1em}(8)}$$
对混沌个体 $x{C}_i^t$ 与原个体 ${\mathrm{ex}}_i^t$, 由下式生成候选 解:
$$x_i^t(\lambda )=\lambda {\mathrm{ex}}_i^t+(1-\lambda )x{C}_i^t,\text{\hspace{1em}(9)}$$
其中 $\lambda$ 为收缩因子, 其值为
$$\lambda =\frac{t_{\max }-t}{t_{\max }}.\text{\hspace{1em}(10)}$$
在得到的候选解 $x_i^t(\lambda )$ 与对应精英个体 ${\mathrm{ex}}_i^t$ 之间 采用贪婪选择策略, 选择优秀的个体 ${\mathrm{ex}}_i^{t^{\prime }}$ 取代当前个 体 ${\mathrm{ex}}_i^t$, 即
$${\mathrm{ex}}_i^{t^{\prime }}=\{\begin{array}{l}{\mathrm{ex}}_i^t,f\left({\mathrm{ex}}_i^t\right)⩽f\left(x_i^t(\lambda )\right)\\ x_i^t(\lambda ),f\left({\mathrm{ex}}_i^t\right)>f\left(x_i^t(\lambda )\right)\end{array}\text{\hspace{1em}(11)}$$
由式(10) 可以看出, 设计的收缩因子 $\lambda$ 随着迭代 次数的增加逐渐减小. 式(9) 表明, $\lambda$ 越小, ${\mathrm{ex}}_i^t$ 对候选 解 $x_i^t(\lambda )$ 的影响越小. 因此, 算法随着迭代次数的增 加, 精英个体的上下界范围逐渐缩小至目标解附近, 候选解 $x_i^t(\lambda )$ 越侧重随机性、多样性较强的混沌个 体 $x{C}_i^t$, 局部搜索能力越强. 精英个体的混沌变异策 略所控制的混沌搜索范围随算法迭代次数的增加逐 渐缩小, 实验验证该策略具有较强的局部搜索能力.

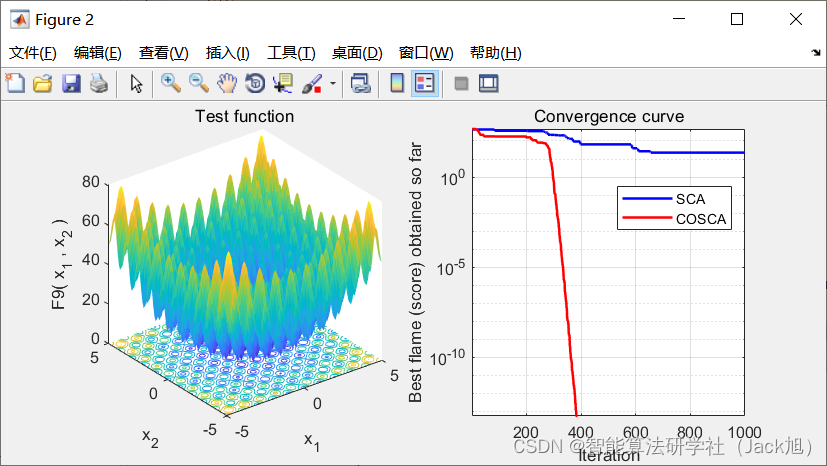
基于精英混沌搜索策略的交替正余弦算法(COSCA)步骤如下：

Step 1: 算法参数设置. 种群规模 $N$, 控制参数 $a$ 的初始值 $a_{\text{start }}$ 和最终值 $a_{\text{end }}$, 最大化迭代次数 $t_{\max }$，调节系数 $\eta >0$, 精英选择比例pr.
Step 2: 初始化. 令 $t=0$, 随机在解搜索空中产生 $N$ 个个体, 组成种群 $G$.

Step 3: 对 $G$ 中的个体执行式 (4) 的反向策略, 形 成种群 $\bar{G}$, 计算 $\bar{G}\cup G$ 中个体的函数值, 按从小到大 排序, 选择前 $N$ 个个体组成初始种群 $G^t$, 并记录最优 个体 $x_{\ast }^t$.

Step 4: 若 $t$ 为奇数, 则执行 Step 4.1; 若 $t$ 为偶数, 则 执行 Step 4.2:

Step 4.1: 对 $G^t$ 中的个体执行 $\mathrm{SCA}$ 算法, 其中控 制参数 $r_1$ 如式 (3) 所示, 对个体按适应度值由小到大 排序得到种群 $G_z^{t+1}$;

Step 4.2: 对 $G^t$ 中的个体进行式 (4) 的 OBL 策略 更新得到 ${\bar{G}}^t$, 对 $\bar{G}\bigcup G$ 中的个体按函数值从小到大 排序, 选择前 $N$ 个个体组成种群 $G_z^{t+1}$.

Step 5: 对 $G_z^{t+1}$ 中的前 $m$ 个精英个体进行式
(5) (11) 所示的精英混沌搜索, 其余 $N-m$ 个个体 不变,形成种群 $G^{t+1}$.

Step 6: 记录 $G^{t+1}$ 中最优个体 $x_{\ast }^{t+1}$, 若 $f\left(x_{\ast }^t\right)<$ $f\left(x_{\ast }^{t+1}\right)$, 则 $x_{\ast }^{t+1}=x_{\ast }^t$.

Step 7: 判断算法是否满足结束条件, 若满足, 输 出最优值 $f\left(x_{\ast }^{t+1}\right)$, 否则令 $t=t+1$, 转至 Step 4 .

3.实验结果

4.参考文献

[1]郭文艳,王远,戴芳,刘婷.基于精英混沌搜索策略的交替正余弦算法[J].控制与决策,2019,34(08):1654-1662.

5.Matlab代码

6.python代码