提供了编程的基础技术教程

zl程序教程

您现在的位置是：首页 >  后端

当前栏目

浅析算法的时间复杂度和空间复杂度 (C++/python双语实例)

PythonC++实例算法 时间 空间 浅析 复杂度
2023-09-14 09:01:28 时间

目录

时间复杂度

时间复杂度的概念

大O的渐进表示法

常见的时间复杂度举例

空间复杂度

如何衡量一个算法的好坏呢？
一个算法如果写的十分的短，是不是就非常的好呢？

例如斐波那契数列：

C++:

#include <iostream>
#include <iomanip>
#include <cmath>
 
using namespace std;
 
#define M_SQRT5      2.2360679774997896964091736687313
#define M_1pSQRT5_2  1.6180339887498948482045868343656
 
long double Fibo(size_t n)
{
	return round((pow(M_1pSQRT5_2,n)-pow(1-M_1pSQRT5_2,n))/M_SQRT5);
}
 
int main(void)
{	
    for (long n=1;n<=100;n++)
    	cout<<n<<"\t= "<<setprecision(21)<<Fibo(n)<<endl;
 
	cout << "... ..." << endl;
 
    for (long n=1470;n<=1480;n++)
    	cout<<n<<"\t= "<<setprecision(21)<<Fibo(n)<<endl;
 
	return 0;
}

python:

def Fib(n:int)->int:
    return 1 if n<3 else Fib(n-1)+Fib(n-2)

 以上代码，c++和python的主体函数都只有一行return语句，一个是使用数列通项公式（又称比内公式），一个使用递归法；前者局限于long double的精度，后者局限于递归层数的限制。

通常情况下，计算斐波那契数列多数会使用数列定义的递推公式来递归，但当n大于30时计算就非常吃力了；想要计算第100万项的值基本上是不可能的了。

>>> from time import time
>>> for i in range(30,40):
	t=time();n=Fib(i);print(i,time()-t)

	
30 0.42186927795410156
31 0.6874938011169434
32 1.1093668937683105
33 1.7812433242797852
34 2.8906190395355225
35 4.640621185302734
36 7.48436975479126
37 12.109369277954102
38 19.6406192779541
39 31.74999499320984

用Fib(n-1)+Fib(n-2)递归只能一项项往前推，太慢了；我样可以这样改进，用斐波数列的性质（如下所示）来递归，效率明显提升：计算第10万项秒杀，第100万项20秒以内。

由 F(1)=F(2)=1; F(n)=F(n-1)+F(n-2) 推导出：

F(2n)=F(n+1)*F(n)+F(n)*F(n-1) ; F(2n+1)=F²(n+1)+F²(n)

>>> def Fib(n:int)->int:
    if n<3: return 1
    if n%2: return Fib(n//2)**2+Fib(n//2+1)**2
    return Fib(n//2)*(Fib(n//2+1)+Fib(n//2-1))

>>> from time import time
>>> t=time();n=Fib(100);print(time()-t)
0.0
>>> t=time();n=Fib(1000);print(time()-t)
0.015600204467773438
>>> t=time();n=Fib(10000);print(time()-t)
0.062400102615356445
>>> t=time();n=Fib(100000);print(time()-t)
0.9536018371582031
>>> t=time();n=Fib(1000000);print(time()-t)
18.566032886505127

此函数已知项只有F(1)、F(2)两项，若增加已知项的项数也能提升一点效率，计算第100万项的值只要3秒不到：

>>> def Fib(n:int)->int:
    if n<11: return [0,1,1,2,3,5,8,13,21,34,55][n]
    t=n//2
    if n%2: return Fib(t)**2+Fib(t+1)**2
    return Fib(t)*(Fib(t+1)+Fib(t-1))

>>> from time import time
>>> t=time();n=Fib(1000);print(time()-t)
0.0
>>> t=time();n=Fib(10000);print(time()-t)
0.017600059509277344
>>> t=time();n=Fib(100000);print(time()-t)
0.22040081024169922
>>> t=time();n=Fib(1000000);print(time()-t)
2.76320481300354
>>>

那么我们要用什么方式去衡量一个算法的好坏，所以我们引进了时间复杂度和空间复杂度。 时间复杂度主要衡量一个算法的运行快慢，而空间复杂度主要衡量一个算法运行所占用空间。
 

时间复杂度

时间复杂度的概念

衡量一个算法的运行时间快慢也就是时间复杂度，那么计量的单位是什么？如果用我们常用的时间单位例如：秒、毫秒。这就存在一个问题，不同机器由于配置不同时间会不相同，而且要想知道时间就必须上机跑代码很麻烦。所以我们把算法花费的时间与其中语句执行次数成正比，算法中的基本操作执行个数，为算法的时间复杂度。

>>> def fun(n:int)->None:
	count = 0;
	for i in range(n):
		for j in range(n):
			count += 1
	for i in range(n*2):
		count += 1
	m = 10
	while m:
		count += 1
		m -= 1
	print(count)

	
>>> fun(10)
130
>>> fun(100)
10210
>>>

由这个函数中的全局变量count，我们很容易知道执行了F(N)=N^2+2*N+10
其实我们在计算精确的执行次数，而只需要大概执行次数，这里我们使用大O的渐进表示法。

大O的渐进表示法

大O符号（Big O notation）：用于描述函数渐进行为的数学符号。常见复杂度如下：

复杂度标记符号描述
常量（Constant） O(1) 操作的数量为常数与输入的数据的规模无关。
对数（Logarithmic） O(log2 n) 操作的数量与数据的规模 n 的比例是 log2 (n)。
线性（Linear） O(n)操作的数量与数据的规模 n 成正比。
平方（Quadratic） O(n2)操作的数量与数据的规模 n 的比例为二次方。
立方（Cubic） O(n3)操作的数量与数据的规模 n 的比例为三次方。
指数（Exponential） O(2n) O(n!)指数级的操作，快速的增长。

 大O复杂度操作数曲线：

常见的时间复杂度举例

例一：常量级

C++:

#include<iostream>
using namespace std;

int func(int n){
	int i = 0;
	for(int j=0;j<1000;i++,j++);
	return i;
}

int main(void){
	cout << func(100) << endl;
	cout << func(1000) << endl;
	
	return 0;
}

python:

>>> def fun(n:int)->int:
	i = 0
	for j in range(1000):
		i += 1
	return i

>>> fun(100)
1000
>>> fun(1000)
1000

时间复杂度为O(1000)但是如果为常数的话，时间复杂度可以直接写为O(1)

例二：阶乘之和 1!+2!+3!+...+n!

C++:

#include<iostream>
using namespace std;

long long func(int n){
	long long sum = 1;
	for(int i=n;i>1;i--){
		sum *= i;
		sum += 1;
	}
	return sum;
}

int main(void){
	cout << func(10) << endl;
	cout << func(20) << endl;
	
	return 0;
}

python:

def factSum(n):
    Sum = 1
    for i in range(n,1,-1):
        Sum *= i
        Sum += 1
    return Sum

def factSum2(n):
	Sum = 0
	from math import factorial as fact
	for i in range(1,n+1):
		Sum+=fact(i)
	return Sum

时间复杂度为O(N)

例三：冒泡排序

C++:

#include<iostream>
#include<cmath>
using namespace std; 

int main(void) { 
	double a[100];
	int N; 
	int i = 0, j = 0;
	cin >> N;

	for (i = 0; i<N; i++)
		cin >> a[i];

	for (i = 0; i<N - 1; i++) { 
		for (j = 0; j<N - 1 - i; j++)
		{
			if (a[j]>a[j + 1]) {
				int tmp;
				tmp = a[j];
				a[j] = a[j + 1];
				a[j + 1] = tmp;
			}
		}
	}

	for (i = 0; i<N; i++){
		cout << a[i] << " "; 
	}
	cout << endl;
	
	return 0;
}

python:

>>> def Bubble(a:list)->None:
	for i in range(len(a)-1):
		for j in range(len(a)-1-i):
			if a[j]<a[j+1]:
				a[j],a[j+1]=a[j+1],a[j]

				
>>> b = [*range(1,6)]
>>> Bubble(b)
>>> b
[5, 4, 3, 2, 1]
>>>

由这个程序我们可以知道F(N)=N-1+N-2+.....+1=(N^2-N)/2

例四：二分查找

C++:

template<class T>  

int Binary_Search(T *x, int N, T keyword)  
{  
    int low = 0, high = N-1,mid;  
    while(low <= high)  
    {  
        mid = (low + high)/2;  
        if(x[mid] == keyword)  
            return mid;  
        if(x[mid] < keyword)  
            low = mid + 1;  
         else  
            high = mid -1;  

    }  
    return -1;  
}  

int Binary_Search2(int *a, int low, int high, int key)  
{  
     if(low > hign) 
          return -1;
     int mid = (low + high) / 2;  
     if(a[mid] == key)  
          return mid;  
     if(a[mid] > key)  
          return Binary_Search2(a, low, mid-1, key); 
     else  
          return Binary_Search2(a, mid+1, high, key);
}

python:

def binSearch(a:list,x:int):
	left,right = 0,len(a)
	while left<=right:
		mid = (left+right)//2
		if x>a[mid]:
			left = mid+1
		elif x<a[mid]:
			right = mid-1
		elif x==a[mid]:
			return mid
	return -1

这个算法对于每次查找，找不到就会将范围缩小二倍，时间复杂度也就是O(log2 N)

例五：递归阶乘

C++:

#include<iostream>
using namespace std;

long long func(int n){
	long long sum = 1;
	for(int i=n;i>0;i--)
		sum *= i;

	return sum;
}

int main(void){
	cout << func(10) << endl;
	cout << func(20) << endl;
	
	return 0;
}

python:

>>> def F(n:int)->int:
	if n: return F(n-1)*n
	return 1

>>> F(0)
1
>>> F(1)
1
>>> F(2)
2
>>> F(3)
6
>>> F(4)
24
>>> F(5)
120
>>>

这个也非常简单return的 值为F(N-1)*F(N-2)........F(0)一共是N+1个，所以中间的代码也就执行了N+1次，所以时间复杂度是O(N)

例六：斐波那契数列

C++:

#include<iostream>
using namespace std;

long long func(int n){
	if (n<3) return 1;
	return func(n-1)+func(n-2);
}

int main(void){
	cout << func(10) << endl;
	cout << func(20) << endl;
	
	return 0;
}

python:

def F(n:int)->int:
    if n<3: return 1
    return F(n-1)+F(n-2)

这个函数的时间复杂度很多文章都说它是指数级O(2ⁿ)的，但我还是用python全局变量法来测试：

>>> def F1(n):
	global count
	count += 1
	if n<3: return 1
	return F1(n-1)+F1(n-2)
 
>>> count=0; F1(20),count
(6765, 13529)
>>> count=0; F1(25),count
(75025, 150049)
>>> count=0; F1(30),count
(832040, 1664079)
>>> 6765*2,75025*2,832040*2
(13530, 150050, 1664080)
>>> 6765*2-1,75025*2-1,832040*2-1
(13529, 150049, 1664079)
>>>

看全局变量n终值的测试结果，可知： F(n)的运算次数 = 2*F(n) - 1，其中F(n)的通项公式（也就是比内公式）为：

 F(n) = \frac{1}{\sqrt{5}}[ (\frac{1+\sqrt{5}}{2})^{n} - (\frac{1-\sqrt{5}}{2})^{n} ]

再来使用cProfile库函数Profile()来验证一下：

>>> from cProfile import Profile
>>> def F(n:int)->int:
    if n<3: return 1
    return F(n-1)+F(n-2)

>>> cp = Profile()
>>> cp.enable(); n = F(30); cp.disable()

>>> cp.print_stats()
         1664081 function calls (3 primitive calls) in 0.708 seconds

   Ordered by: standard name

   ncalls  tottime  percall  cumtime  percall filename:lineno(function)
1664079/1    0.708    0.000    0.708    0.708 <pyshell#7>:1(F)
        1    0.000    0.000    0.000    0.000 rpc.py:614(displayhook)
        1    0.000    0.000    0.000    0.000 {method 'disable' of '_lsprof.Profiler' objects}


>>> 2*F(30)-1
1664079
>>> 2**30
1073741824
>>> 30**3
27000
>>>

结果cp.print_stats()输出的function calls的值正好也等于2*F(30)-1，所以我认为这个函数的时间复杂度应在立方级O(n³)和指数级O(2ⁿ)之间，比O(n³)大好几十倍但要比O(2ⁿ)小两到三个数量级，实际上应该是这样一个“数量级”：

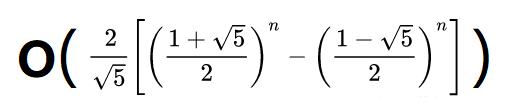
空间复杂度

空间复杂度也是一个数学表达式，是对一个算法在运行过程中临时占用储存空间大小的度量。

空间复杂度不是程序占用了多少bytes空间，因为这个也没太大意义，所以空间复杂度算的是变量的个数。也用O（）来表示。

注意：函数运行所需要的栈空间在编译的时候就已经确认好了，因此空间复杂度主要通过函数在运行时显示申请的空间来确定。

例一：冒泡排序

源代码略（参见上一节内容空间复杂度，以下同）实际上这里开辟的空间只有i，j  所以空间复杂度为O(1)。

例二：阶乘函数

答案是O(N)
这里如果对函数栈帧不是很了解的话，这个原理也就不会知道。函数栈帧可以简单的理解为：函数每被调用一次，都会在栈区上开辟一块空间，所以F(N)会调用F(N-1)，F(N-1)会调用F(N-2)…同时会调用N个F，每个F都会开辟一块空间，所以空间复杂度为：O(N)。

示例三：斐波那契数列

通过上面的实例我们就可以知道斐波那契数列实际上开辟了N个Fib函数空间，只是这些函数空间会被重复利用，总共被运行2^n-1次，所以空间复杂度为：O(N)。

（本篇完）

相关文章