引言：

北京时间：2023/5/13/10:13，饥肠辘辘，为了将红黑树的博客赶出来，导致现在还没有吃早饭，所以现在先容我去吃一下早饭，ok，转眼一看，12:25，哈哈哈，时间过的真快啊，那是因为我吃完早饭，实在是忍不住摆烂，去睡了一觉，睡到刚刚，应该不是自然醒，算是给热醒的，哈哈哈，并且又到了吃中午饭环节，为了降低摆烂的可能，先不吃饭，先码字3000，码完字再说，不然非常容易导致，在吃饭的时候，打开腾讯视屏，看电视，最后把我刚睡醒的精力给搞没，然后又犯困，最终在心里暗示下，怡然自得，合情合理的去睡午觉，坚决不能让这样的事情发生，所以先容我吃个面包垫一垫，然后我们就进入该篇博客的学习，并且该篇博客，我们合情合理，顺水推舟的学习一下有关AVL树的相关知识和代码实现

AVL树非代码实现相关知识

什么是AVL树

上篇博客，我们解决了红黑树的相关知识和代码，本来是应该先学AVL树再学红黑树，这样就可以降低我们在理解红黑树中旋转相关知识的成本，因为AVL树控制平衡的方法就是不断的旋转，通过不断的旋转，来保证每个结点的左右子树的高度差的绝对值小于2，所以AVL树的特点就是左右子树高度差的绝对值小于2，根据这一点特征，我们也可以把AVL树叫做旋转树或平衡旋转树，但是莫慌，谁让我是在学完AVL树的基础上学习的红黑树，所以红黑树的旋转对于我来说还是没什么学习成本滴，哈哈哈，只是写博客的顺序发生了一些的调整，谁让红黑树的名气那么大，搞的我很想先写红黑树，再写AVL树，并且注意：AVL树的实现方法有很多，此时我们用的是较好理解的三叉链（有父结点指针）和平衡因子的方式，此时的平衡因子就是用来记录左右子树的高度差，进而利用该平衡因子来进行判断左右子树是否满足高度差绝对值小于2这个AVL树的硬性条件，满足则合理，不满足则通过旋转让它合理，所以我们学习AVL树代码实现的本质不是学会代码的编写，代码的编写没有任何用处，我们要学习的是AVL树控制住平衡的方法，如何通过旋转来实现 O(logN) 的时间复杂度，如下图就是一颗AVL树的结构图：

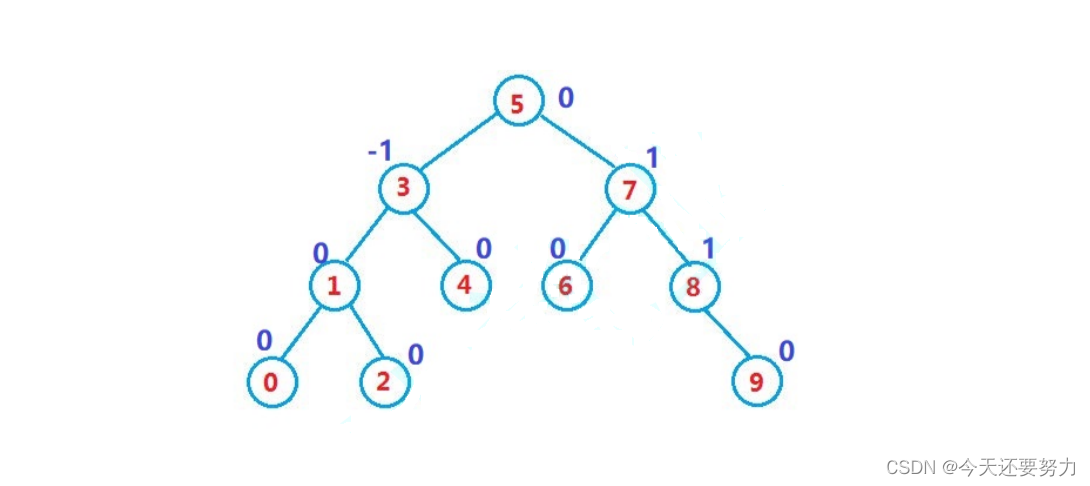
总：AVL树的实现就是需要利用好平衡因子，通过判断平衡因子，从而控制该左右子树是否需要旋转，在一定发生旋转的情况下，最终通过不同的场景，来控制最终发生怎样的旋转（左单旋、右单旋、左右双旋、右左双旋）

AVL树代码实现相关知识

AVL树结点的创建

哈哈，还是那句话，任何类型的数据结构，都有一个与之对应的结点，如上篇博客中红黑树的结点，其中的 _color 对象就是红黑树结点最明显的特征，当然AVL树同理，拥有自己的结点（不同的实现方法可能会导致结点不同），所以接下来就让我们看看AVL树的结点有什么特殊之处吧！如下图所示：

当然一定要有较强的抽象思维，不能单单只是被眼前的几个对象给迷惑住了，一定要看出它们在代码中的用处，比如此时的平衡因子，它不就是一个整形类型的普通数据吗？为什么它叫平衡因子呢？所以这就是我们的抽象思维，我们将左右子树的高度差给抽象成了结点中的一个整形数据，此时_balancefactor代表不仅仅是一个整形类型的对象了，它代表的就是右子树的高度 - 左子树的高度，当然你也可以抽象成左子树的高度 - 右子树的高度，本质没有区别，代码控制上仅仅是++变成- -，- -变成++，如下图所示：

AVL树插入接口实现

同理，行文来到这里，此时就要明白，AVL树首先是一个搜索二叉树，其次因为它控制住了平衡，所以也是一棵平衡搜索树，所以在插入结点的过程还是同理于搜索二叉树，通过判断对应结点的key值，来找到合适的空位置，从而插入数据，具体代码如下所示：

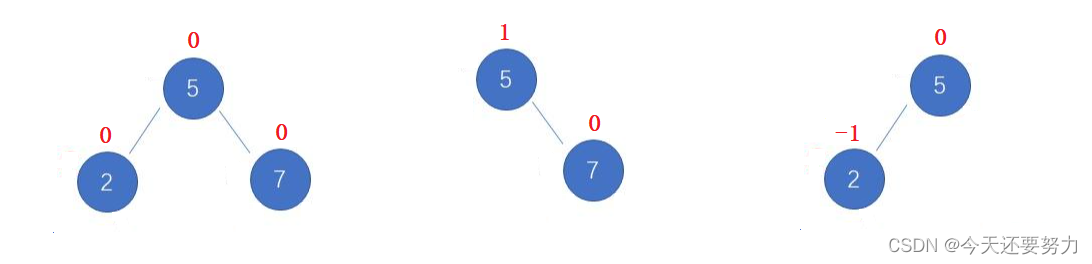
明白了上述知识，同理进入该篇博客的重点，如何通过平衡因子控制搜索树的平衡，首先明白任意一个结点插入时，它的平衡因子都是初始化为0，所以此时第一步肯定是需要根据对应的场景去改变平衡因子的值，也就是如果某一个结点插入在了根结点的右子树且该结点的左子树没有结点，那么此时该根结点的平衡因子就需要改变，从0变成1，反之从0变成-1，当然也可能是插入结点时，该根结点有左孩子或者右孩子，那么此时平衡因子依然需要改变，从1变成0，或者从-1变成0，具体如下图所示：

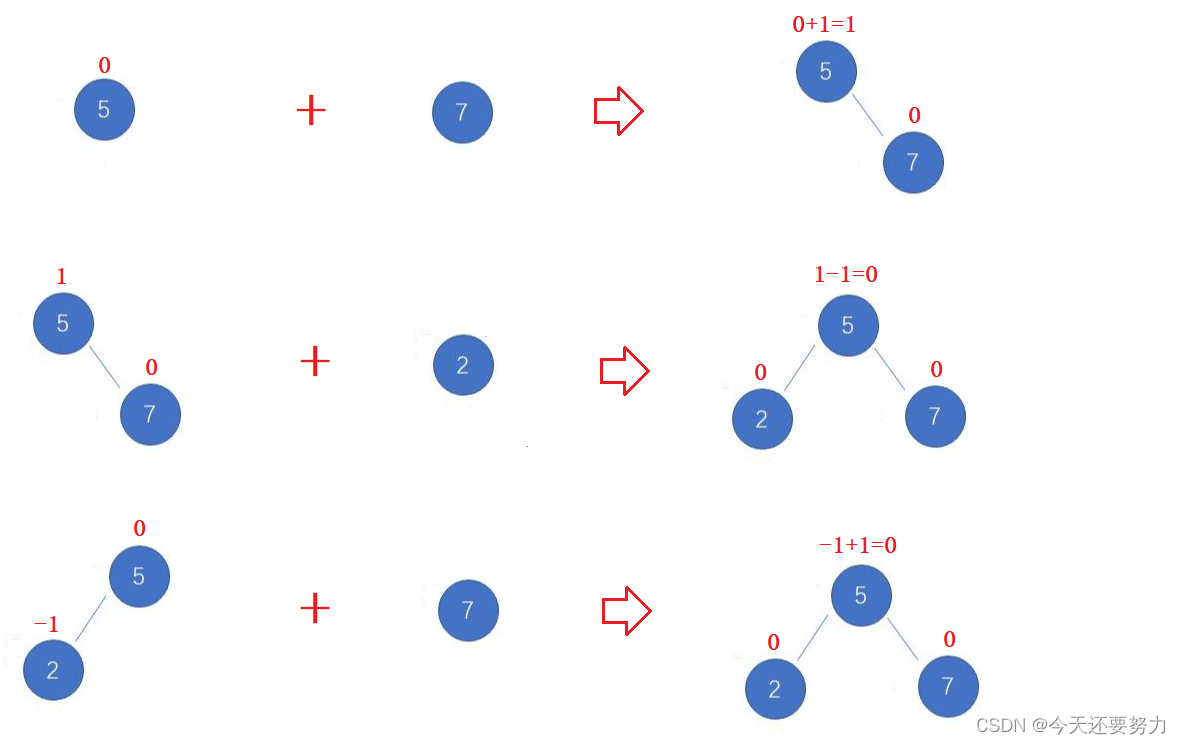
明白了这个道理，那么此时我们应该如何使用代码来控制平衡因子的加加和减减呢？如下代码所示：但是此时值得注意的是，插入一个结点，父结点的平衡因子一定会被改变，祖先结点的平衡因子可能会被改变，也可能不会被改变，具体改变还是不改变，取决于父结点是否有孩子结点，如果有孩子结点，那么此时插入结点，父结点的平衡因子就会从1或者-1变成0，从而导致该子树从原理的相对平衡变成了绝对平衡，所以此时不会影响爷爷结点的平衡因子，但是如果当父结点没有孩子结点时，此时父结点的平衡因子就会从0变成1或者-1，从绝对平衡变成相对平衡，此时就会影响到爷爷结点的平衡因子，同理向上推断，直到_root结点停止，当然，如果想要到达_root结点前提是所有的祖先结点除了父结点都拥有孩子结点，否则在到达_root结点之前，就会由于平衡因子绝对值大于1而被终止掉，意思就是，当某一个结点的平衡因子绝对值大于1时，此时该子树就失衡了，此时不需要继续去更新平衡因子，而是要先将该子树调整，也就是旋转该子树，具体过程请看下文，这里不多做讲解

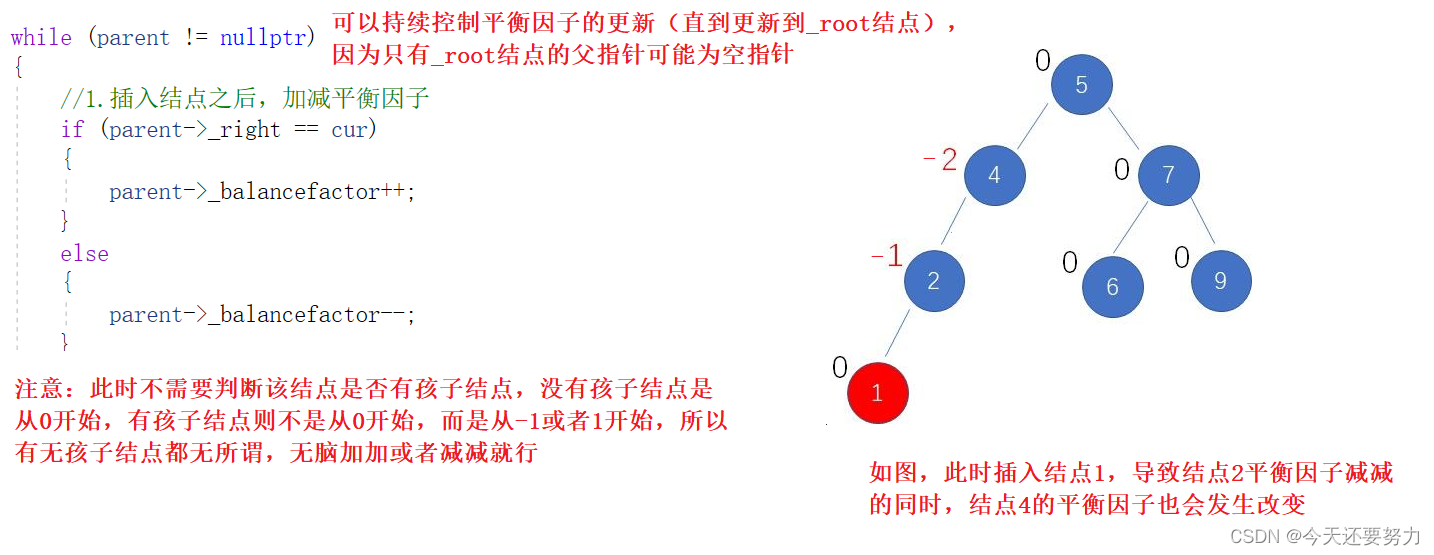
综上所述：此时我们就明白了，在插入结点之后的更新平衡因子过程中，如果父亲结点的平衡因子为0，就说明该结点所处的子树处于绝对平衡，父结点平衡因子的改变，不会影响祖先结点，而如果父结点的平衡因子为1或者-1，则说明，该子树处于相对平衡，那么此时就需要继续向上更新爷爷结点的平衡因子，并且注意：如果此时爷爷结点有孩子结点，那么爷爷结点也可以处于相对平衡状态，反之，则是失衡状态，此时就需要进行旋转调整，具体旋转过程下文详细讲解，所以明白了这些场景，此时我们就可以通过条件判断，把这些场景通过具体的条件控制住，如下代码所示：

正式进入旋转场景

注意：想要进行旋转，那么此时父结点的平衡因子（迭代过后）一定是2或者-2，一是因为只有当父结点的平衡因子为2或者-2，才需要旋转，二是因为旋转之后，该子树就平衡了，父结点平衡因子为0还是1或-1，具体由旋转场景决定，所以在AVL树中不可能会出现平衡因子为3或者4之类的结点
话不多说，此时旋转场景一共分为四种：左单旋、右单旋、左右双旋、右左双旋，此时我们就将这四种旋转分为两类，虽然本质上旋转方法都相同

单旋

正式进入单旋的学习，明白为什么要单旋和什么时候要单旋，单旋的目的不难看出就是为了降低子树的高度，从而让其满足AVL树的特性，那么什么时候要单旋呢？有的人会说，当某个根结点的平衡因子为2或者-2的时候就要进行单旋，当然这是对的，因为这是旋转发生的前提，但是此时我们要明白的是什么时候会发生单旋，所以想要发生单旋，那么首先必须要插入结点，在插入结点的过程中，通过直接判断结点插入的位置，来判断是否发生单旋，如下图所示：

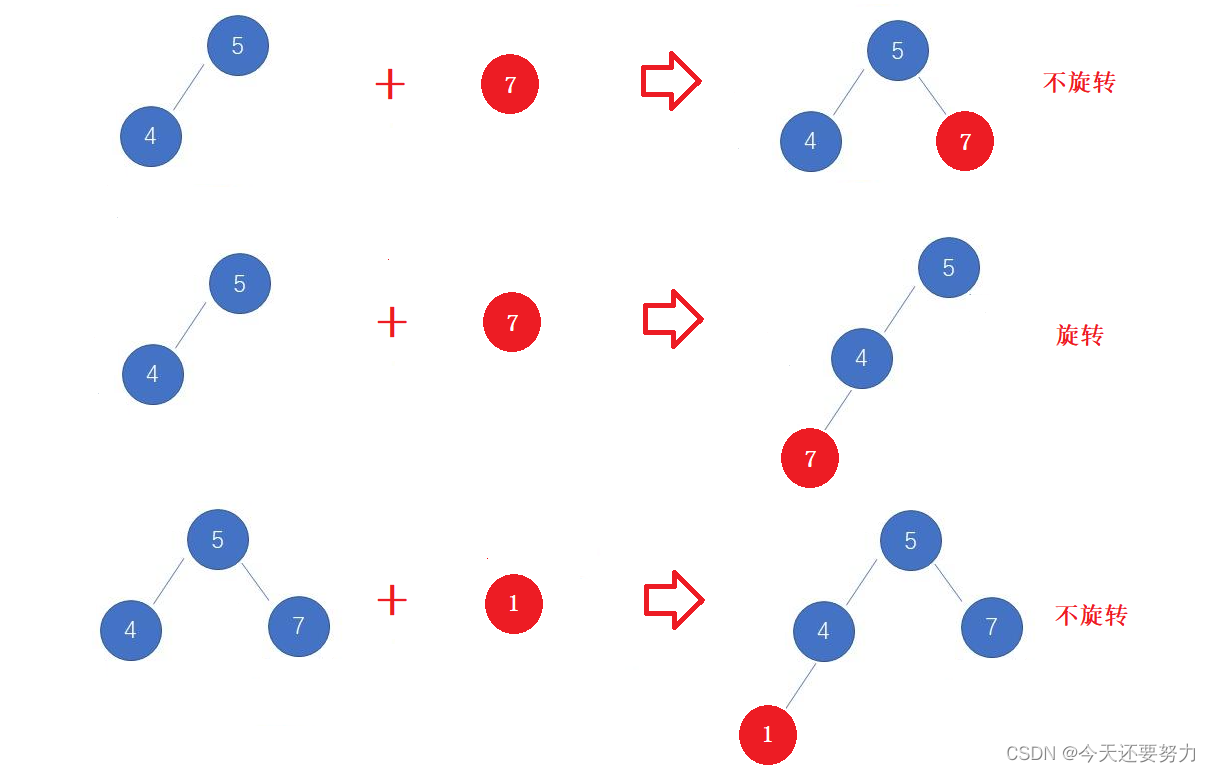
所以我们发现，想让一棵子树发生单旋，那么此时这棵子树在没有插入结点之前，根结点的平衡因子就必须为1或者-1，并且插入结点必须要插入在高度高的那一侧的同侧（本质就是让平衡因子从-1或1变成-2或2），注意：必须是插入在高度高的那一侧的同侧，否则就不是单旋，而是双旋（前提是根结点的平衡因子已经是1或者-1），如下图所示：

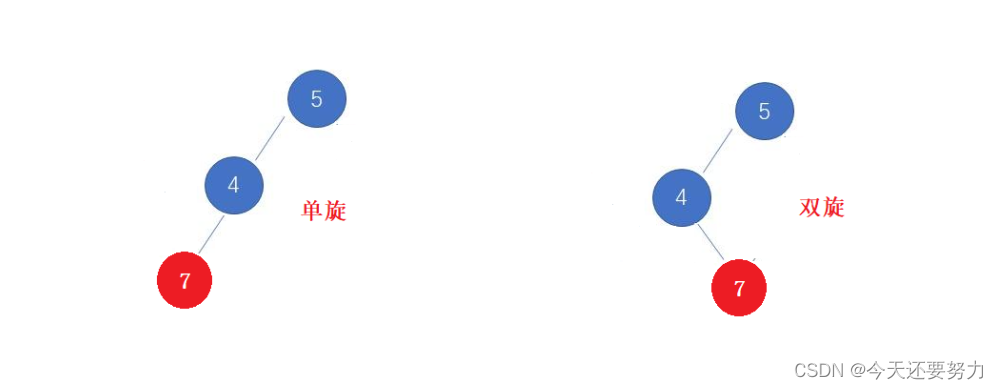
明白了上述知识，对于什么时候发生旋转，什么时候发生单旋？我们就有了更深的认识，此时就让我们进入抽象图和具象图的理解，看到更多有关单旋的插入场景，从而找出发生单旋的规律，进而控制代码，并且明白，左单旋和右单旋本质上没有区别，只是平衡因子一个是正一个是负，所以单旋的讲解我们以右单旋为例，左单旋同理，如下图：

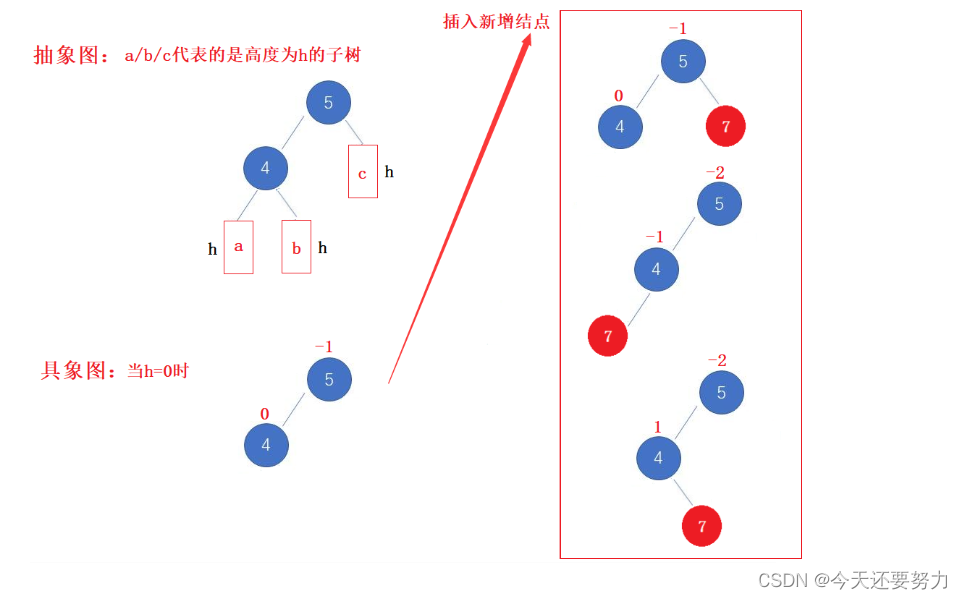
从上图可以发现，当h=0时，表示的就是此时该AVL树没有任何的子树，所以此时它一共有三个位置可以插入数据，5的右侧，4的左侧和4的右侧，但是我们发现，只有当数据插入在了4的左侧，此时才会发生单旋，并且此时发生单旋时，parent结点的平衡因为是-2，cur的平衡因子为-1（需要迭代向上更新平衡因子），所以我们可以有一定的猜想（前提是根结点的平衡因子是1或者-1），当parent的平衡因子为-1（同侧）且pparent的平衡因子为2时，发生的就是单旋（右单旋）（当然大前提同侧不同侧取决于parent结点是左子树还是右子树），但此时我们是如上图所示看待，并且无论是左单旋还是右单旋，同理看待，所以接下来就让我们来看看当子树高度为1时，具体有哪些单旋场景，看是否和上述猜想相符合，如下图：

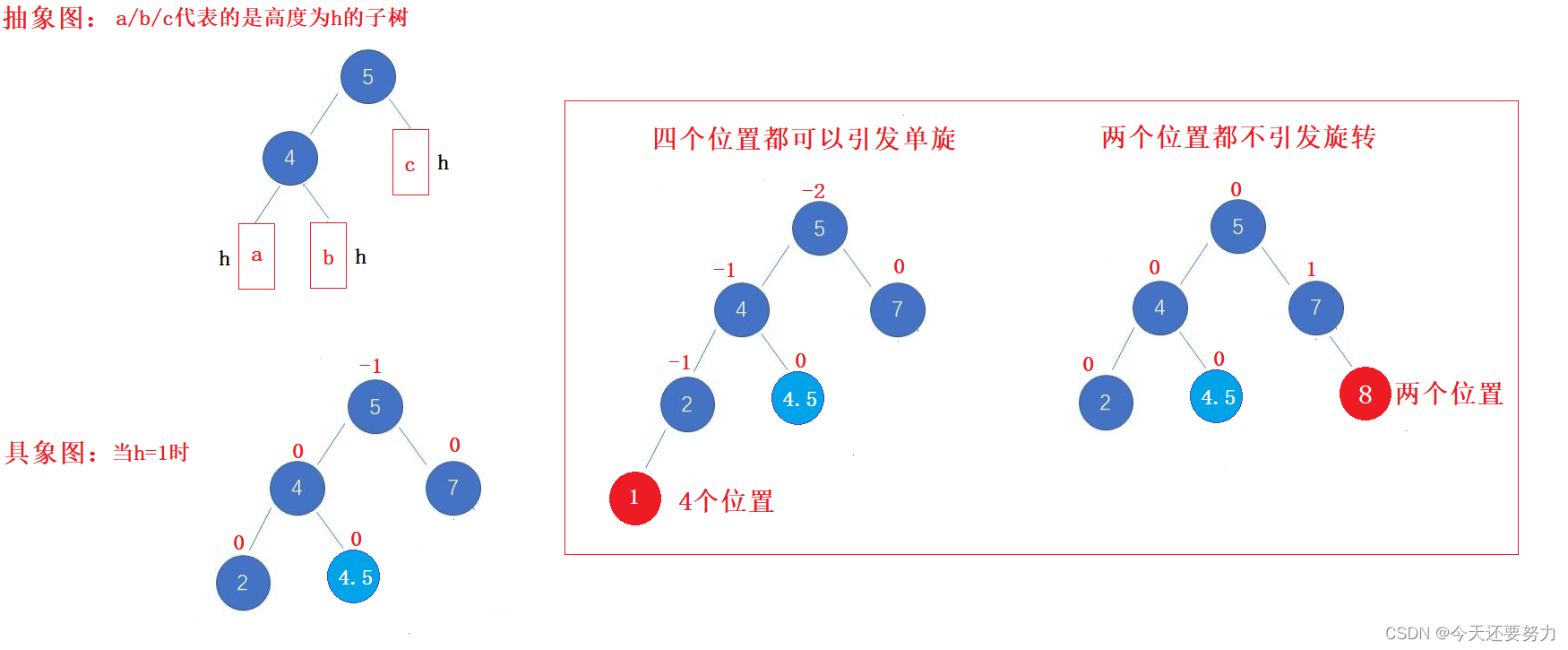
如上图，此时我们可以发现，当h=1时，此时的场景从h=0时的3个变成了6个，并且此时有4个位置会插入数据会引发单旋，且发现由于父结点原来的平衡因子为0，插入结点之后变成了-1，所以此时一定会影响爷爷结点的平衡因子，需要迭代向上更新平衡因子，所以此时的cur位置就变成了结点2，parent位置就变成了4，然后发现4结点的平衡原来也是0，插入数据之后变成了-1，所以需要再一次向上更新，此时的cur就变成了结点4，parent变成了5，最终在不断向上迭代更新平衡因子的过程中，发现parent的平衡因子为-2，cur的平衡因子为-1， 完全符合我们上述对h=0时，发生单旋场景的判断，所以此时我们继续深入，看看h=2时具体有哪些单旋场景吧！如下图：

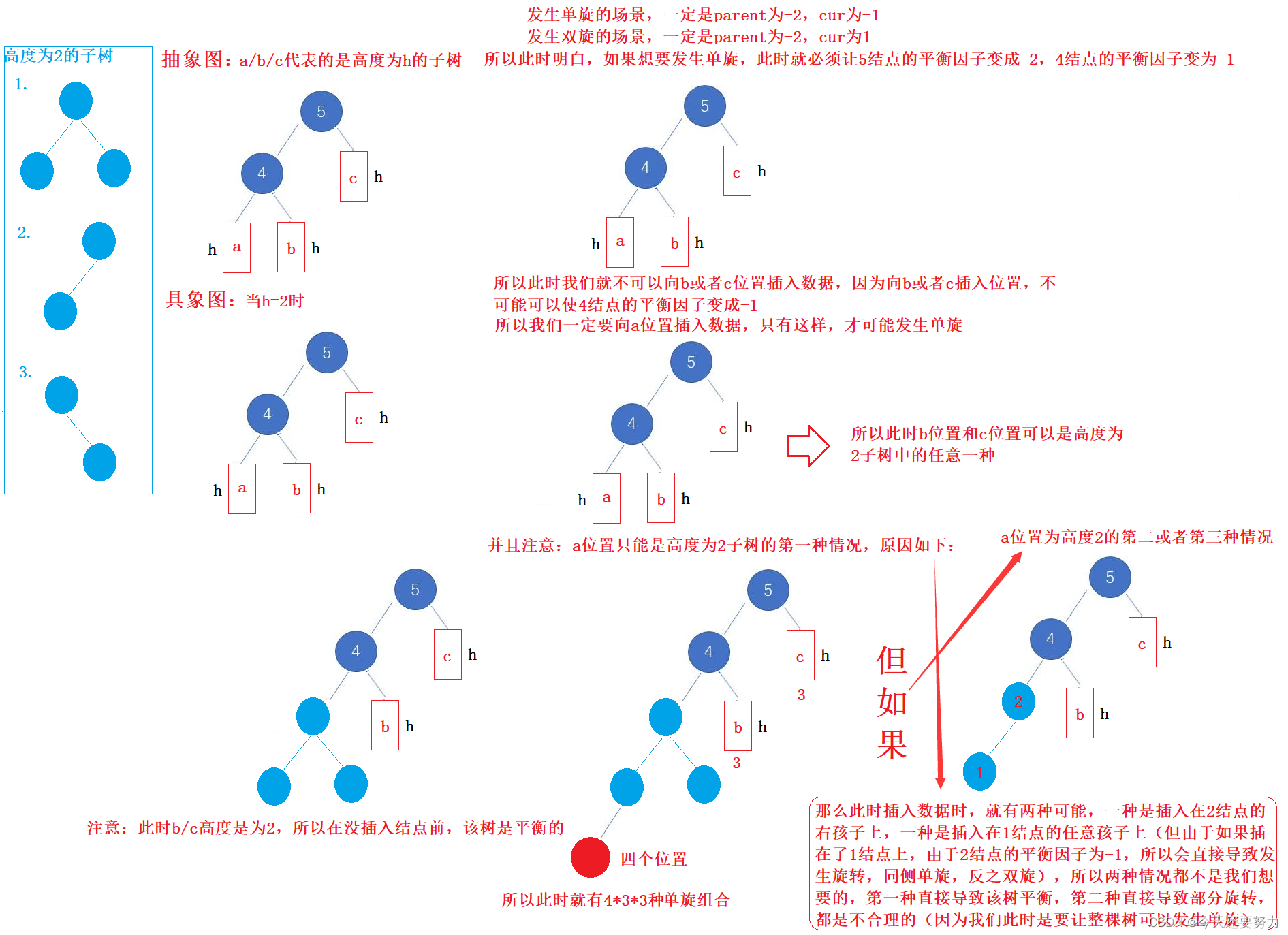
可以发现，当h=2时，发生单旋的场景就有36种之多，但是通过我们对其规律的掌握，此时还是同理，上图无论是那种单旋场景，最终都需要迭代去更新祖先结点的平衡因子，发现最终，parent结点的平衡因子永远都是-2，cur结点的平衡因子都是-1，所以这就是单旋在AVL树中最重要的特征，从上述这么多图中明白了这点之后，同理，左单旋，不过只是右子树的高度比左子树高而已，所以插入数据之后发生的就是左单旋，得出左单旋在AVL树中最重要的特征只是parent结点的平衡因子为2，cur的平衡因子为1而已

综上所述：发生左单旋的情况就是parent结点的平衡因子为2，cur结点的平衡因子为1，发生右单旋的情况就是parent结点的平衡因子为-2，cur结点的平衡因子为-1

如何单旋

明白了上述有关单旋的具体场景，此时我们就来看看具体是如何进行单旋的，如下图所示：

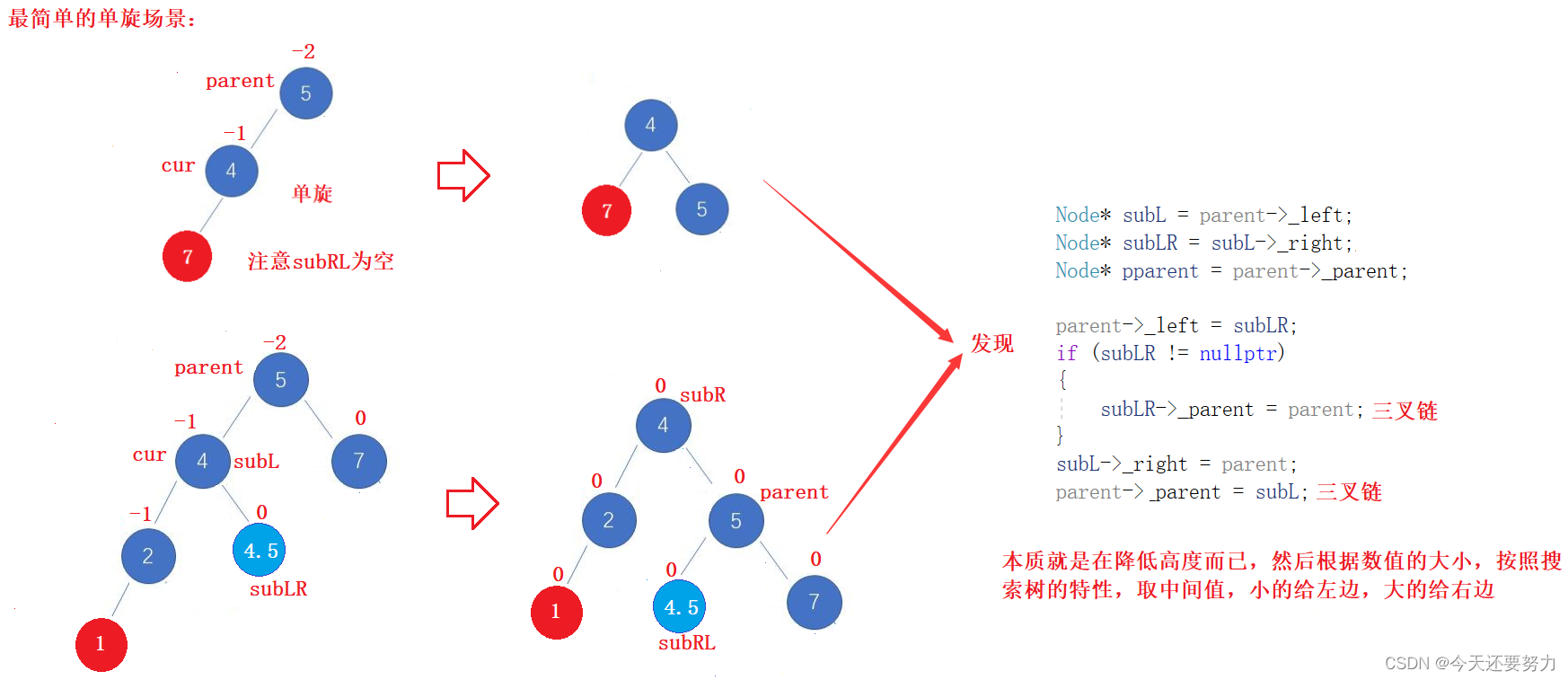
单旋具体代码

右单旋：

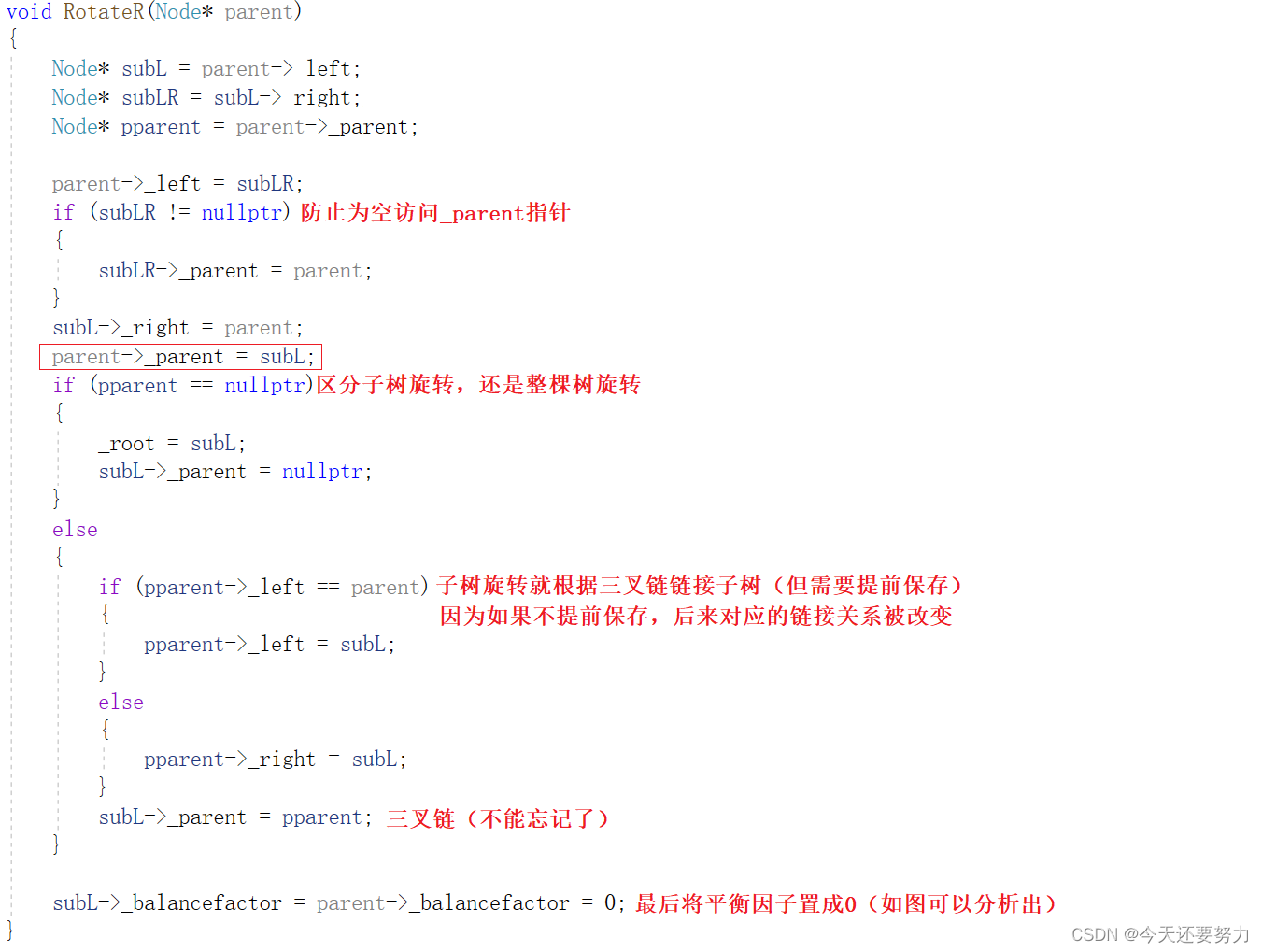
左单旋：

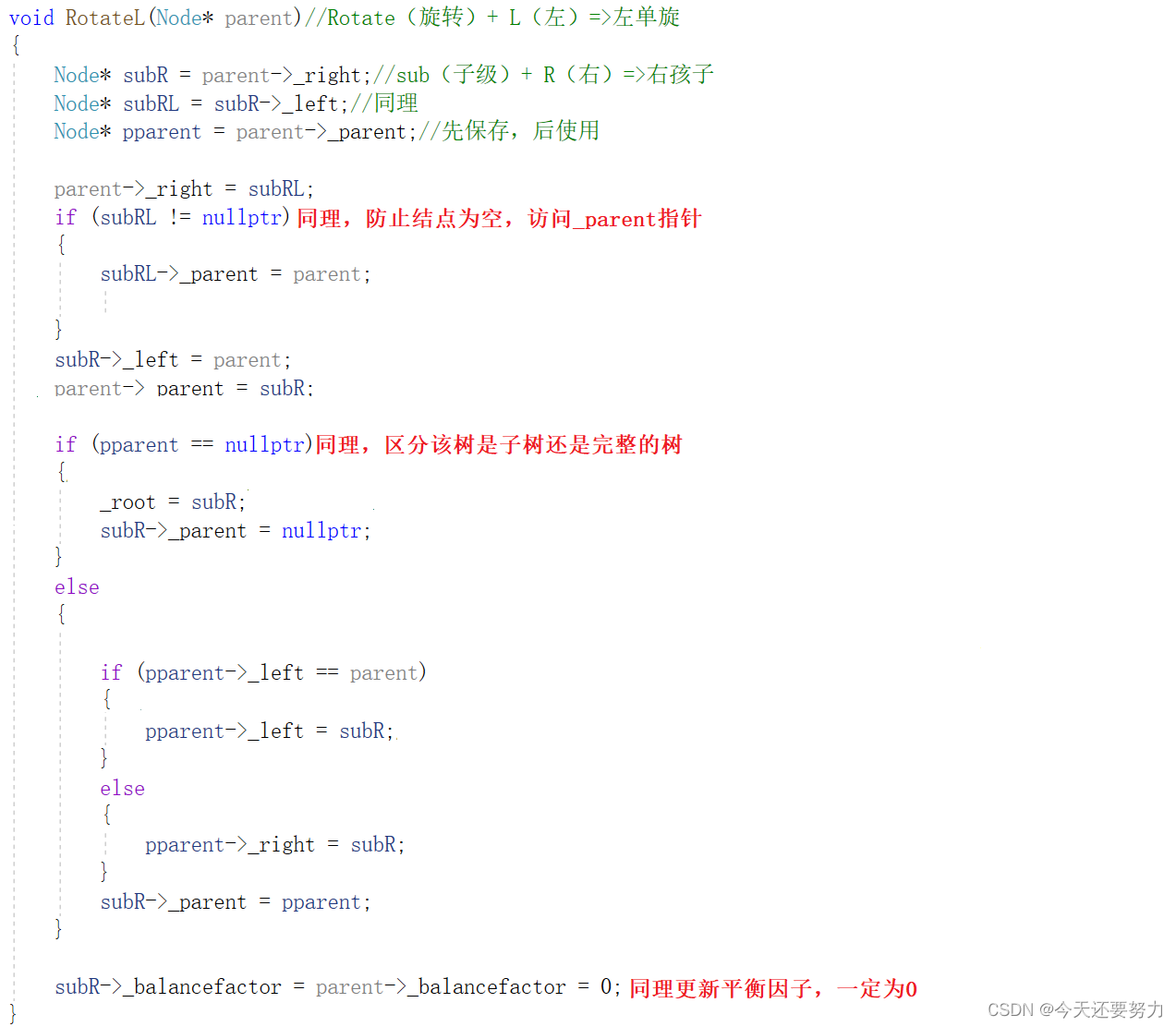
双旋

明白了上述有关单旋的所有知识，搞定双旋还不是三下五除二的事情，因为双旋的本质就是两个单旋而已，并且通过上述知识，此时我们明白了，无论是单旋还是双旋，本质上的场景何其之多，所以我们不能通过控制场景来控制什么时候单旋，什么时候双旋，我们必须通过对不同场景的分析，找到一定的规律，从而通过控制这些规律，来控制具体的旋转情况，如上述parent为-2，cur为-1时我们就右单旋，parent为2，cur为1时，我们就左单旋，同理，此时我们要去发现双旋的规律，具体如下图所示：

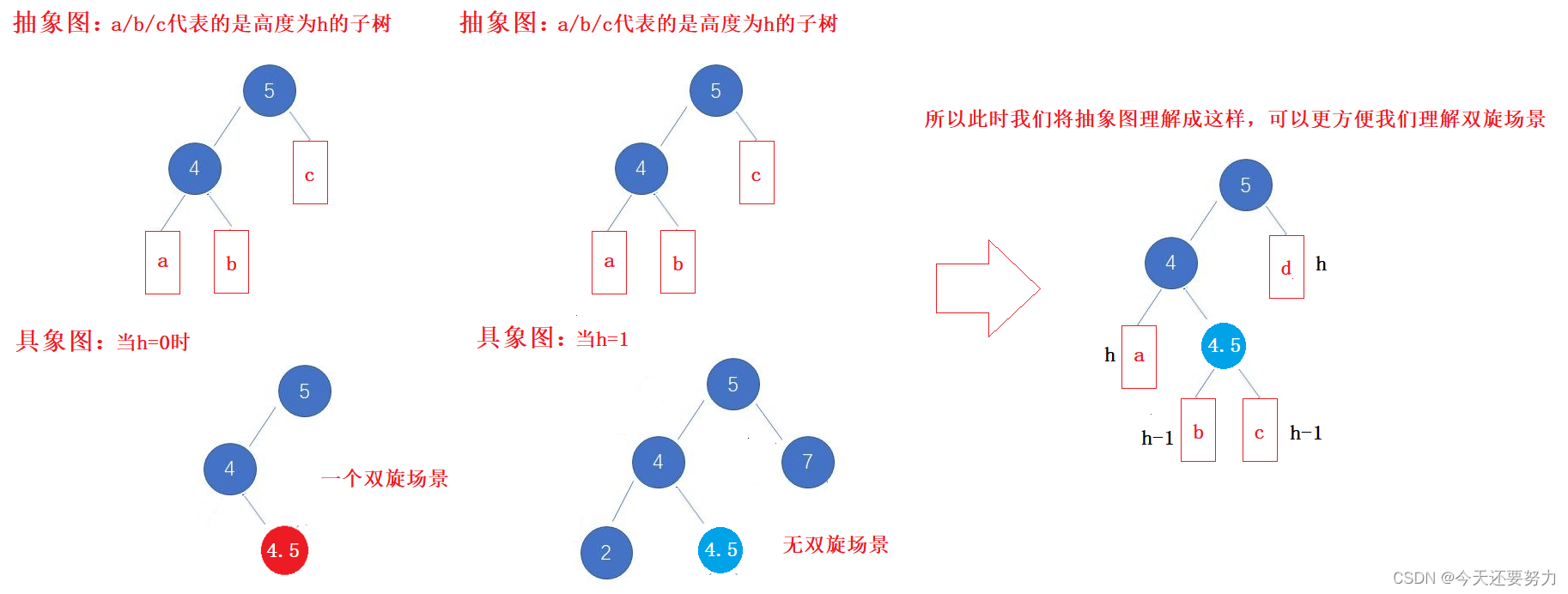
明白了上述知识，此时我们正式进入到双旋具象图的理解，如下图所示：

可以看出当h=0时，不需要插入任何数据，抽象图就已经是一个双旋场景，这也是为什么我们要把高度给成h-1的原因，并且通过对每一个结点的平衡因子分析，发现，此时parent结点的平衡因子是-2，cur结点的平衡因子是1(迭代向上更新了平衡因子)，所以我们大致可以猜想，当parent结点和cur结点的平衡因子满足该条件时，发生的就是双旋场景（左右双旋），所以接下来，就让我们深入h=1和h=2时的场景，看看更多的有关双旋的具象图场景，如下图：

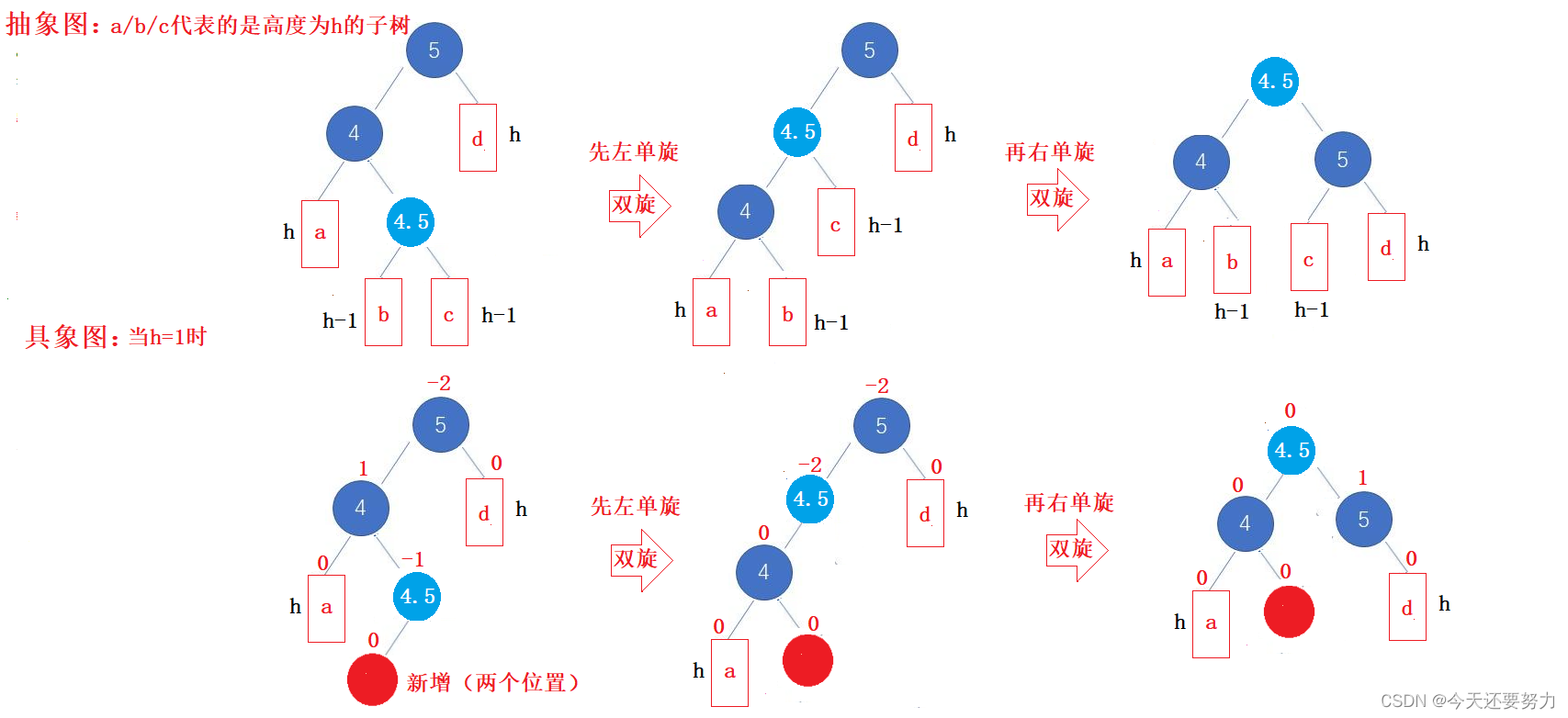
同理，此时我们发现，当h=1时，有两个位置插入会导致整棵树发生双旋，并且无论这两个位置是那个位置进行插入，最终parent结点的平衡因子都是-2，cur结点的平衡因子都是1，所以我们得出结论，当parent结点的平衡因子为-2，cur结点平衡因子为1时，此时发生的就是双旋场景

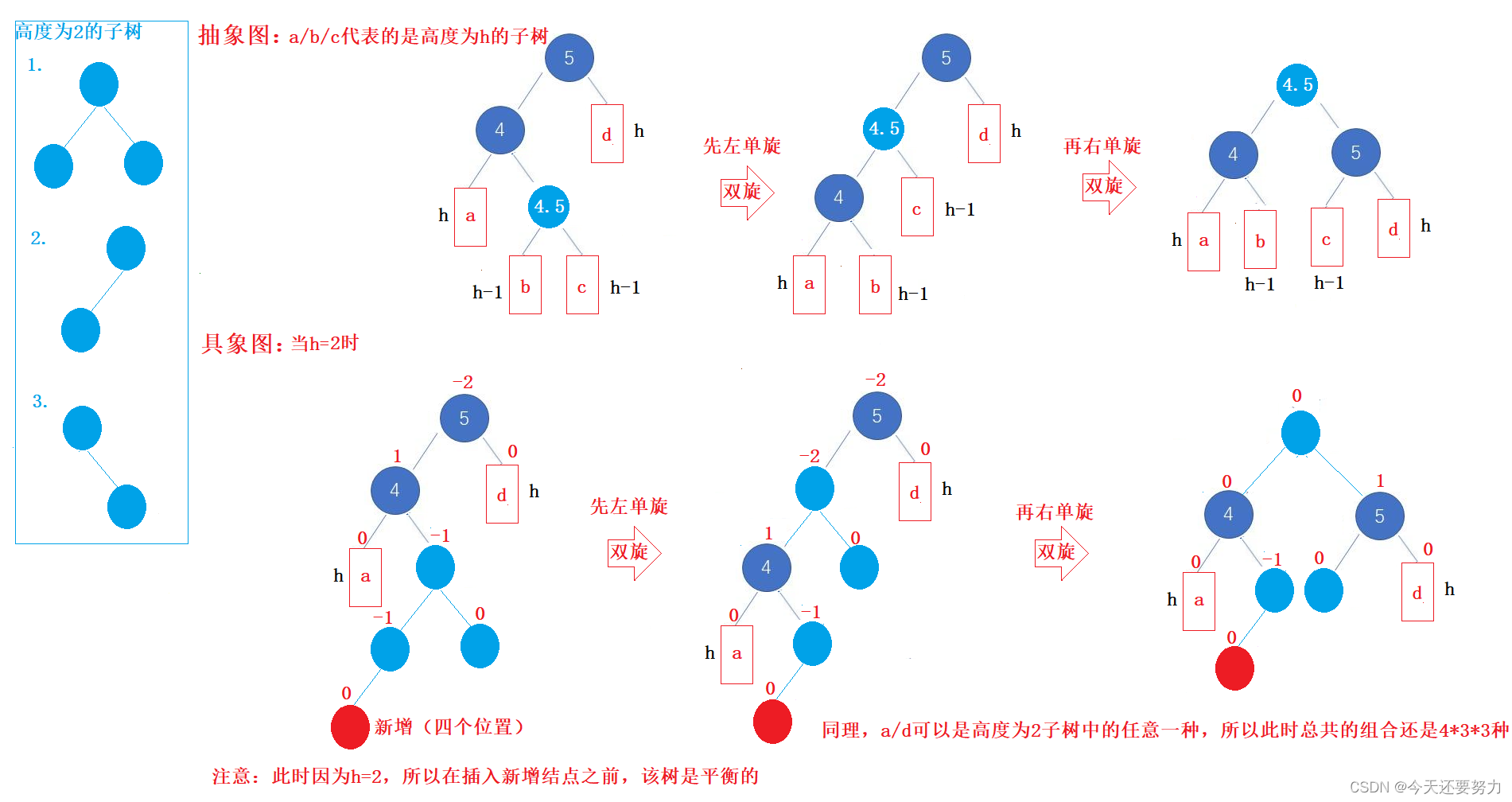
同理，当h=2时，有四个位置插入结点会导致整棵树发生双旋，所以当h=2时，总共就有36种情况会导致双旋，同理上述图示都是左右双旋，右左双旋同理，所以导致发生右左双旋场景，就是parent结点的平衡因子为2，cur结点的平衡因子为-1

综上所述：发生左右双旋的情况就是parent结点的平衡因子为-2，cur结点的平衡因子为1，发生右左双旋的情况就是parent结点的平衡因子为2，cur结点的平衡因子为-1

双旋具体代码如下：

明白，双旋就是两个单旋，明白单旋的旋转过程，此时双旋的旋转过程，我们就不多做讲解了，具体就是看一下双旋的代码如何控制就行，值得注意的是：在双旋过程中，由于插入结点的位置不同，导致链接的位置不同，也就是导致最终有一个结点的平衡因子会变成1或者-1，具体根据插入位置判断，如下代码所示：

左右双旋：

右左双旋：

同理，不多做画图

验证该树是否是AVL树

1.判断平衡因子是否正确
2.判断每棵子树高度差的绝对值是否小于等于1

具体代码：

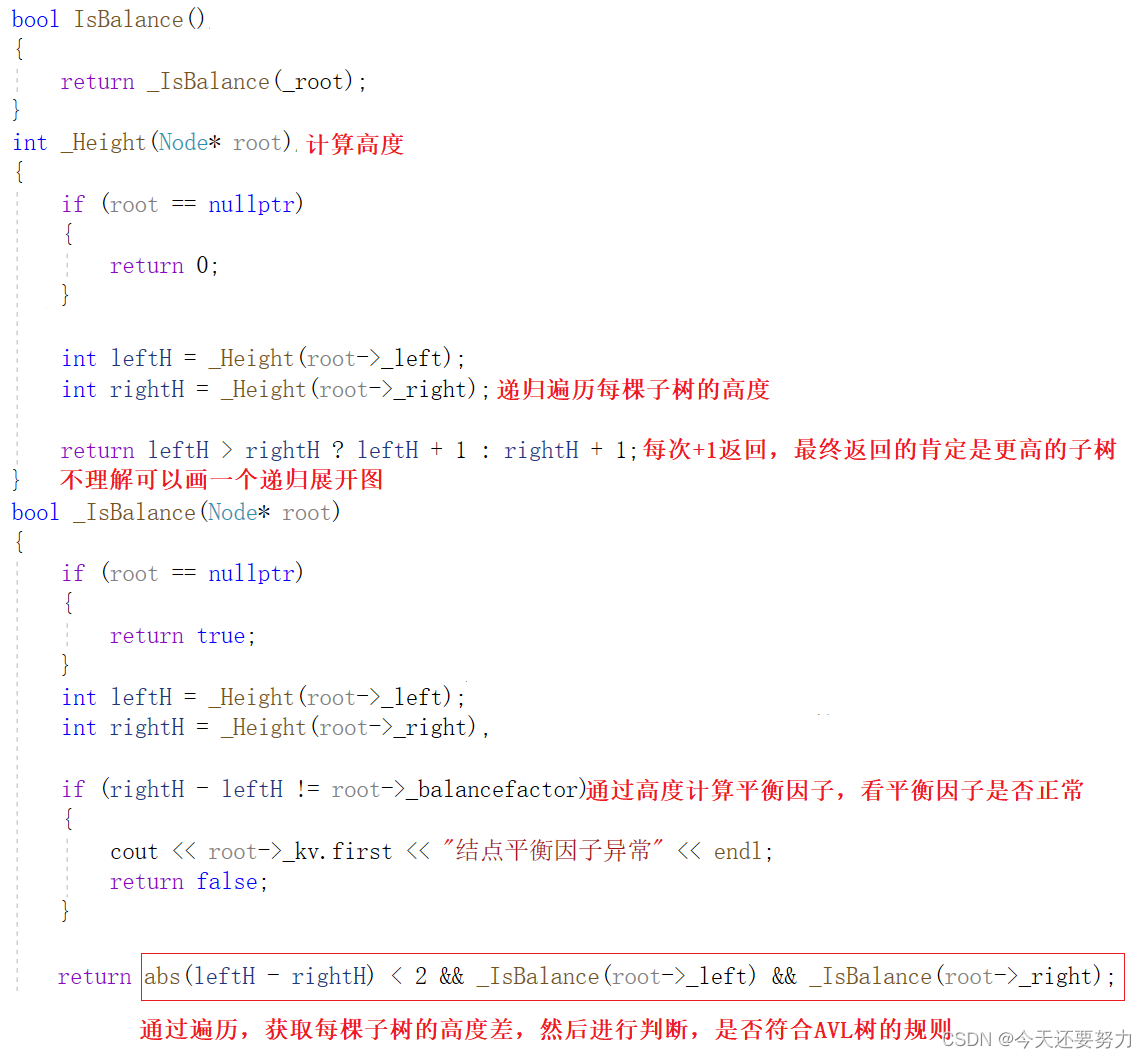
AVL树插入接口实现完整代码和注释详解（循环）

#include<iostream>
#include<string>
#include<vector>
#include<set>
#include<map>
#include<cassert>
#include<time.h>

using namespace std;
//AVL树结点构建
template<class K,class V>
class AVLTreeNode
{
public:
	AVLTreeNode<K, V>* _left;
	AVLTreeNode<K, V>* _right;
	//K _key;
	//V _value;//前几个参数同理搜索树
	//并且因为学习过set和map，所以此时这里直接用pair结点
	pair<K, V> _kv;

	AVLTreeNode<K, V>* _parent;//三叉链
	int _balancefactor;//平衡因子(控制每个结点的高度，右子树-左子树)

	AVLTreeNode(const pair<K,V>& kv)
		:_left(nullptr), _right(nullptr), _parent(nullptr), _kv(kv), _balancefactor(0)
	{}
};

//非递归实现
template<class K, class V>
class AVLTree
{
	typedef AVLTreeNode<K, V> Node;
public:
	AVLTree()
		:_root(nullptr)
	{}
	bool Insert(const pair<K, V>& kv)//这个位置莫要惊慌，只要把pair看成是一个自定义对象就行，只是加了一个const和引用
	{
		//前一小部分的代码同理搜索树
		if (_root == nullptr)
		{
			_root = new Node(kv);
			return true;
		}
		Node* parent = nullptr;
		Node* cur = _root;
		while (cur != nullptr)
		{
			if (cur->_kv.first < kv.first)
			{
				parent = cur;
				cur = cur->_right;
			}
			else if (cur->_kv.first > kv.first)
			{
				parent = cur;
				cur = cur->_left;
			}
			else 
			{
				return false;
			}
		}
		//循环来到这里，一定要清晰知道表示什么意思，表示的就是找到了大小合适的空结点位置
		cur = new Node(kv);
		//if (parent->_kv.first > cur->_kv.first)
		if (parent->_kv.first > kv.first)//这个写法等价于上述写法，本质都是同一个值
		{
			parent->_left = cur;
		}
		else
		{
			parent->_right = cur;
		}
		cur->_parent = parent;//三叉链结构规定（本质是为了便与之后更新父结点高度），因为如果插入一个结点，最终导致高度改变的，只能是该结点的祖先结点
		//代码来到这里，搜索树代码全部正常完成，此时多的情况就是AVL树的代码了（如何控制住平衡）

		//一定注意：此时我们是在创建一棵树，不是修改一棵树（代码思路要清晰）
		//具体样例：	
		//           5
        //        3    7
        //      1  4  6  8
        //     0 2        9
		//此时我们就通过该样例图，来推断出控制平衡的各种场景和条件
		//此时引入第二个关键变量（平衡因子）
		//知道，如果插入数据之后，平衡因子更新完成之后，平衡因子_balancefactor绝对值<1表示平衡结构没有受到影响，不需要处理
		//如果_balancefactor平衡因子绝对值>1，表示平衡结构受到影响，则需要处理（旋转，较为复杂，AVL树门槛）

		//此时引出不平衡需要调整问题（但在搞定该问题之前，此时我们要明白平衡因子具体改变情况）

		//如下：
		//平衡因子改变情况，以上图为例，插入一个结点，观察平衡因子的改变，具体可能场景如下：
		//1.当在9的右结点插入一个结点，此时可以发现，不仅仅是9的平衡因子发生改变从0变成了1,8平衡因子从1变成了2，而是该结点的所有祖先结点的平衡因子都发生了改变
		//同理在8的左结点插入，也会导致该结点的所有祖先的平衡因子发生改变
		//2.当在8的左结点插入一个结点，此时发现，仅仅只是8的平衡因子从1变成了0,7和5这两个祖先结点的平衡因子并没有发生任何的改变
		//总：当插入一个新结点时，此时会影响到别的结点的平衡因子（部分或者全部）

		//得出该结论，此时我们就明白了更新平衡因子时的部分条件，如下代码所示：
		//当然在更新平衡因子之前，我们要知道，如果新增结点在根结点的左边，那么平衡因子减减，右边，平衡因子加加

		while (parent != nullptr)//这个条件表示的就是持续控制平衡因子的更新（直到root->_parent == nullptr;）
		{
			//1.插入结点之后，加减平衡因子
			if (parent->_right == cur)
			{
				parent->_balancefactor++;//注意：此时是每一个结点都有对应的平衡因子，该平衡因子不是一个全局变量，所以要记得具体指明是那个结点
			}//并且明白，不需要区分该结点有没有孩子结点，就是无脑加，原因：没有孩子结点，插入结点，加加，很正常，但是如果有孩子结点，此时也要加加或者减减，因为有孩子结点，此时它的平衡因子就不是0了，而是1或者-1，所以应该加加，让它变成0
			else
			{
				parent->_balancefactor--;
			}
			//代码来到这里，我们要考虑的就是，更新完该结点，还需不需要继续更新上面的祖先结点
			//面对一个问题，什么决定了要向上更新，什么决定了不要向上更新  方法：通过判断插入结点的父结点的_balancefactor（高度）是否发生改变（变为0除外），变了就向上更新，没变就不向上更新
			//具体场景：
			//1.插入结点的父结点的_balancefactor（高度）为 1 或者 -1  得出结论：插入结点之后，高度变为 1 或者 -1，说明之前该结点的高度肯定是 0
			//2.插入结点的父结点的_balancefactor（高度）为 0          得出结论：插入结点之后，高度变为0，说明之前该结点的高度肯定是 1 或者 -1
			//3.插入结点的父结点的_balancefactor（高度）为 2 或者 -2  得出结论：如果是该情况，二话不说，开始通过旋转调整
			//4.…… 同理3
			//总：当插入结点之后，高度为 1或者-1，那么该结点就的高度就一定发生过改变（因为AVL树的特性：每个结点的高度只能是0或者1、-1）
			//    并且明白，如果插入结点之后，父结点的高度从 1或者-1 变成了 0，那么此时就不需要向上更新了，因为该结点是0本质并不会影响祖先结点
			//可以结合上上述的两个场景举例来看待这个两个推论              （相对平衡变成了绝对平衡）

			//如何继续更新：同理上述判断代码，只要通过父指针找到对应父结点，然后判断父结点是否为空就行（root结点没有父结点，此时为空）这也就是为什么使用三叉链比较好理解的原因
		
			//2.加减平衡因子之后，控制平衡因子（使其符合AVL树的特性）
			if (parent->_balancefactor == 1 || parent->_balancefactor == -1)
			{
				//继续更新（原理如上）
				parent = parent->_parent;
				cur = cur->_parent;
			}
			else if (parent->_balancefactor == 0)//注意：此时是在更新循环中（不更新只能通过跳出循环），并且明白该结点的平衡因子在上述就已经更新过了
			{
				break;//表示不继续更新（原理如上）
			}
			else if (parent->_balancefactor == 2 || parent->_balancefactor == -2)//因为如果是一棵AVL树，它的平衡因子只能是0，1或者-1，所以++，--，只会是 2或者-2 ，如果导致了3,4这种情况，那么只能说明这棵树是有问题的，直接assert就行
			{
				//3.旋转调整（目的：降低该子树的高度，让该子树平衡）AVL树的重点
				//具体场景图示：
				//        30
				//      a    60
				//          b  c
				// 此时a/b/c代表的就是抽象出来的子树，并且这些子树的高度为h，所以此时的a/b/c就是抽象的高度为h的子树
				
				//所以可以明白，这些子树（a/b/c）的高度是可以变化的，没有固定（任何可能都有） 
				//当h=0时：                    1
				// 此时该AVL树的具体图示为   30   0
				//                         0    60
				//                             0  0
				// 注意：此时*号代表的是高度为0的子树，也就是表示，这三个位置没有子树，为空
			    //如果结点插入在了b位置或者c位置，那么该树就会从相对平衡变成不平衡，此时就需要进行旋转调整，如下图所示：
				//       2              2
				//    30    -1        30   1
				//       60              60   0
				//     40                   70
				//并且明白，此时上述一共可以有7种子树插入的情况，也就是a，b，c，abc，bc，ab，ac（但是需要调整的只有b，c，bc三种情况而已）

				//当h=1时：                    1
				//此时该AVL树的具体图示为    30   0      (注：*表示的就是子树结点)
				//                         *    60
				//                             *  *      
				//注意：一定要明白，上图*号代表的就是高度为1的子树，也就是该子树只有一个结点，因为一个结点就代表高度为1
				//并且明白，上图的组合此时是处于平衡状态的，只有在对应的结点插入结点，才有可能导致该AVL树失衡
				

				//当h=2时：
				//此时首先要明白，当子树高度为2，此时这棵子树就会有三种不一样的形态，如下：
				//  1.  *   2. *      3.   *
				//   *           *       *   *
				//当使用这些高度为2的结点去构建对应的AVL树时，此时就会有很多中情况，如下为其中之一：
				//              1
				//           30    0
				//         *     6
				//       *  *  *   *
				//           *  * *  *
				// 并且明白：c位置的子树一定是3类型，a/b位置的子树可以是1,2,3任意一种
				// 原因：当在上图所示的平衡树中插入结点，目的就是为了可以让整棵树失去平衡，进行调整（因为此时我们是身处对应的判断语句中）
				// 说明，此时这棵树一定要是不平衡的，否则就不符合我们的要求，不可以是那种部分不平衡，部分平衡，只能是因为对应的根结点
				// 也就是上图中的30结点失去平衡，才可以（因为我们身处的条件就是失去平衡的条件），所以此时c位置一定要是3类型，否则就会因为
				// 是1/2类型导致不能使整棵树失去平衡，而可能会导致，部分失去平衡，如下图所示：
				//               1                1               1
				//            30   0            30   0          30   1
				//          *     6          *      6         *     6  2
				//        *  *  *   *       *  *  *   *      * *   *  *  
				//            *  *   *           * * * *          * *  *  
				//     当c位置不为3类为2类  左结点插入，直接平衡        *  向下插入直接导致上上结点的平衡因子为2，直接发生部分旋转
				// 总：此时在c位置插入数据，无论是如何插入，此时都无法让整棵树发生调整（不符合该条件要求）所以c位置一定要是第三种类型
				// 并且明白，因为此时我们是在单旋的场景下，所以我们只关心同一侧的结点，因为只有当结点在同一侧，此时才是单旋，此时如果把结点插入到了6的左孩子，那么此时就不是单旋，此时就是一个h=0的双旋场景，所以b的位置可以是任意一种，不需要像6的右一样，一定是第三种类型
				// 本质就是：我们是使用6的平衡因子来控制单旋和双旋，如果6的平衡因子为1，才是单旋，如果是-1，直接导致的是双旋
				// 所以在单旋场景，b位置可以是任意类型，因为我根本就不会往6的左孩子插入结点（因为如果插了，此时就走双旋代码），也就是只有往右插入，此时才会导致6的平衡因子变成1，从而走单旋代码	

				//总结：所以我们要控制的场景就是那种，当结点一插入之后，就会导致整棵树失去平衡的组合（前提是这棵树本来就保持平衡）
				
				// 所以我们发现了当h=2时，AVL树的情况就有非常多种组合，所以我们不可能可以通过条件判断，把这些情况给控制住
				// 更何谈当h=3/4/5/6……等的时候，此时AVL树的结点的分布情况可以说是有上万种，所以我们不可以通过结点来调整该AVL树
				//所以此时就得出了下述结论：
				//因为此时我们身处的条件判断就是不平衡的条件，就是需要调整的条件，所以如上述所说当h=1时的7中情况中，除了b,c,bc这三种
				//别的4种情况根本就不会来到该判断条件中，所以无论我的结点这么插，该AVL树的组合到底是那种，我们判断都只是该结点插入之后对应
				//平衡因子的绝对值是否会大于2而已
				//  
				// 具体为什么h=2的时候是36种组合，就是3*3*4=36
				// 
				// 总：我们就是想要搞明白，那些情况会导致30结点的平衡因子变成2
				// 
				// 所以我们不用担心，管它有几种组合，下面代码直接搞定（无论那种情况，处理的规则都是一样的）
				// 本质就是旋转的四种场景而已：如下
				// 1.左单选 如图：
				//     30
				//   h   60
				//     h   h+1     //h同理表示对应高度的子树，h+1表示在该对应高度的子树上插入一个结点（此时这个场景，就可以看做是上述h=0或者h=1后者h=2时的场景）
				//此时可以看出当我们在60的右插入这个结点之后，30的平衡因子就变成了2，所以此时就需要进行更新
				
				//更新方法：将b位置（60的左）变成30结点的右，再让30结点变成60的左，最终60变成该树的根结点（本质是搜索树的特征）原理：根结点右结点的左结点一定比根结点大，根结点一定又比右结点小
				//更新之后：
				//      60
				//    30  h+1
				//   h  h
				
				// 2.右单旋 如图：（注意：左单旋就是链接在左结点，右单旋就是链接在右结点，也就是理解成，右单旋：左边高往右边旋，左单旋：右边高往左边旋）
				//      60             30
				//    30   h         h+1  60
				//  h+1 h                h  h    //明白，此时无论左边是h+1还是右边是h+1都会引发旋转，也就是无论是h还是h+1都可以链接到60的左边
				//一切的一切都同理左单旋
				// 但注意：从左单旋和右单旋可以看出，是需要通过判断出不同的场景来区分到底是走左单旋还是右单旋的，明显的就是根结点的大小（一个是60，一个是30）
				
			    //并且明白，当我们旋转完毕之后，此时根结点的平衡因子就会变成0，如图，所以我们就需要再写一句手动置0的代码
				
				//具体代码如下：
				//注意：此时结点是一个一个的插入的，插入一个结点我们就会进行一次判断，判断该结点的插入是否导致了该树失衡，因为我们是在创建AVL树，不是在修改AVL树
				if (parent->_balancefactor == 2 && cur->_balancefactor == 1)//注意：此时的cur是更新过的，就是parent的左孩子或者右孩子
				{
					RotateL(parent);//如上述条件判断一样，当平衡因子是正的，那么此时就说明，右边更高，所以此时往左边旋转，所以此时就是左单旋
				}
				else if (parent->_balancefactor == -2 && cur->_balancefactor == -1)
				{
					RotateR(parent);//同理，当平衡因子是负的，说明，左边高，就往右边旋转，就说明此时是右单旋
				}
				else if (parent->_balancefactor == -2 && cur->_balancefactor == 1)//满足该条件就是左右双旋，具体如下图所示：
				{
					//同理，左右双旋(本质就是两个单旋)，并且注意：单旋使用的场景，就是单纯的左边高，或者右边高
					//而双旋适用的场景却不同（本质是为了遵循统一的规则进行旋转，可以直接特殊处理，但是不，这样可以让4种旋转保持统一的代码原理）
					//如下图所示：
					//            90
					//          30  *
					//         *  60
					//           *  *
					//同理，如上图所示，*号代表的依然是高度为h的子树
					//当h=0时：
					//           90
					//         30  0
					//        0  60
					//         -1  -1
					//此时可以发现，当h=0时，30的平衡因子是1,90的平衡因子是-2，需要调整，所以此时该树已经是处于失衡状态，60就相当于是我们插入的结点
					// 
					//当h=1时：
					//           90
					//         30  *  h
					//        *  60
					//          *  *  h-1
					//注意：当h=1时，此时上述4棵子树中，60的左和右一定不可以为h，而是要为h-1，因为如果让60的左右结点不为空，也就表示允许插入结点，那么此时就不符合，因为在60左右插入之前，这棵树就已经失衡了
					//需要调整，所以当h=1时，60的左右不可能允许你插入结点，所以只能置为高度为0的子树（也就是空），所以此时60的左右就不允许是高度为h的子树，而一定是要高度为h-1的子树
					//否则就会导致插入结点之前，该数已经是一棵失衡的树（但我们想要的目的是，插入结点之前该树是一棵平衡树，只有当插入结点之后，才导致该树失衡）
					//
					//注意：我们的目的就是：保证插入结点之前该树是一棵平衡树，只有当插入结点之后，才导致该树失衡，进行调整

					//所以此时左右双旋和单旋本质的不同就是，根结点的左子树和右子树的高度差不是1了，而是2（所以在有的位置h一定要给成h-1）
					//所以此时如图所示：
					//           90            进行单旋           30          依然还是不平衡，不符合要求
					//         30  *                            *   90
					//        *  60                               60  *
					//          *  *                             *  *
					//所以此时上述情况，靠单旋就解决不了，一定要使用双旋，具体左右双旋，还是右左双旋看情况
					//并且此时明白，只有在60结点的左和右插入结点才会引发左右双旋，如果是在30的左结点插入结点，引发的就是右单旋，不是双旋
					//正确的旋转方式：（先左单旋，然后右单旋）
				    //           90            进行左单旋           90         然后再进行右单旋         60          完成平衡
					//         30  *                              60   *                              30   90
					//        *  60                             30  *                                *  *  *  *
					//          *  *                           *  *
					//但是注意：此时上述的*号子树结点中，有部分的高度不是h，而是h-1（具体原因：上述详解）
					//如上过程可以看出，双旋的本质就是两次单旋，并且第一次单旋是在为第二次单旋提供条件，构建出一个单旋场景（结点分布在同一侧），然后通过第二次单旋完成平衡
					
					RotateLR(parent);
				}
				else if(parent->_balancefactor == 2 && cur->_balancefactor == -1)//此时明白，结点是传过来的，所以此时的cur是一个固定的位置，不是遍历寻找改变的那个位置
				{
					//同理，右左双旋
					RotateRL(parent);
				}
				else
				{
					assert(false);//assert的条件一定是非0，所以此时这样写，直接报警，这样有利于我们发现错误
				}

				break;//整棵树调整平衡之后，直接break就行，此时就不仅完了插入结点，也完成了平衡
			}

			else
			{
				assert(false);//注意assert的使用，是为真才报错，也就是说明，此时上述的平衡因子判断都有问题，也就是说明，此时该树的平衡因子一来就是不正常的，也就是说明，该树本来就不是平衡树，它的平衡因子并不满足只为0、1或者-1，而是一来就是2,3,4，没有及时进行调整
			}
		}

		return true;
	}
private:
	void RotateL(Node* parent)//Rotate（旋转）+ L（左）=>左单旋
	{//注意此时这个parent参数，调用这个参数就一定是失衡场景（_balancefaotor的绝对值大于2的时候），所以此时表示的就是插入结点所在的子树的根结点的平衡因子变成了2，也就是说只需要把该父结点拿过来，让这个父结点找到对应平衡因子为2的根结点就行（三叉链）
		Node* subR = parent->_right;//sub（子级）+ R（右）=>右孩子
		Node* subRL = subR->_left;//同理
		Node* pparent = parent->_parent;//先保存，后使用

		parent->_right = subRL;//注意：subRL只是表示指针指向的结点，并代表subR->_left这个指针指向（所以此时千万不敢写成subRL = parent）
		if (subRL != nullptr)//（经典场景就是h==0的时候），三个位置任意插入时，就有空情况
		{
			subRL->_parent = parent;//1.由于使用的是三叉链，所以此时需要多更新一个父结点的指向（否则整棵树就乱了）
			                        //2.并且要注意没有左孩子结点时的场景，（也就是subRL为空的场景），为空访问结点对象就是有问题的，所以需要一个判断
		}
		subR->_left = parent;
		parent->_parent = subR;
		//3.此时parent可能是整棵树的根结点，但是也可能是某一个子树的根结点，所以需要进行判断，然后链接
		if (pparent == nullptr)
		{//if (parent->_parent == nullptr)这句代码也是天坑，因为parent已经被更新了，所以不能用了，只能去用之前保存好的地址
			_root = subR;//图示
			subR->_parent = nullptr;//更新父指针（直接使用_root也可以）
		}
		else
		{
			//Node* pparent = parent->_parent;(这句代码的位置是个坑，由于上述我们已经把parent链接到了surR的左边，所以此时pparent代表的就是subR，是不合理的，所以要提前定义，也就是提前保存)
			if (pparent->_left == parent)
			{
				//pparent->_left = parent;(这句也是天坑代码)
				pparent->_left = subR;//此时是让你更新头结点，不是让你重新链接一遍，不敢当大聪明
			}
			else
			{
				pparent->_right = subR;
			}
			subR->_parent = pparent;//更新父指针（三叉链带来好处的同时，带来的不便）
		}

		subR->_balancefactor = parent->_balancefactor = 0;
	}

	void RotateR(Node* parent)              //      30      右单旋场景，左单旋不一样，左单旋的结点大小不同      30
	{                                       //    15   *                                                      *    60
		Node* subL = parent->_left;         //   *  *                                                             *  *
		Node* subLR = subL->_right;//场景不同，才可以的导致代码原理相同
		Node* pparent = parent->_parent;

		parent->_left = subLR;
		if (subLR != nullptr)
		{
			subLR->_parent = parent;
		}
		subL->_right = parent;
		parent->_parent = subL;
		if (pparent == nullptr)
		{
			_root = subL;
			subL->_parent = nullptr;
		}
		else
		{
			if (pparent->_left == parent)
			{
				pparent->_left = subL;
			}
			else
			{
				pparent->_right = subL;
			}
			subL->_parent = pparent;
		}

		subL->_balancefactor = parent->_balancefactor = 0;
	}
	void RotateLR(Node* parent)
	{
		//RotateL(parent->_left);
		//RotateR(parent);
		//但是此时这种写法，无法控制每个结点的平衡因子，所以不可以直接这样写

		//所以我们需要自己控制平衡因子
		Node* subL = parent->_left;
		Node* subLR = subL->_right;
		int balancefactor = subLR->_balancefactor;//先记录好平衡因子，再去旋转

		RotateL(parent->_left);//明白双旋就是两个单旋，此时只要知道具体旋转的是那个子树，把对应子树的头结点传过来就行
		RotateR(parent); //旋转之后，parent就是我们要的右旋头结点（图）

		//旋转完之后，更新平衡因子（因为旋转接口默认置0了）
		if (balancefactor == 1)//注意：此时这个平衡因子代表的结点是对应位置插入结点的父结点，并且如果该结点的平衡因子是1就表示，此时结点插入在该结点的右孩子
		{
			parent->_balancefactor = 0;//90 => 旋转之后成为了右子树的根，此时就需要具体判断，看h-1+1结点链接到了30上，还是90上，发现如果balancefactor=1，表示结点插入在了右孩子，并且因为此时右孩子会被旋转链接到到90上，所以此时90的平衡因子是1,30的平衡因子由于链接的是h-1，所以是-1
			subLR->_balancefactor = 0;//60  => 旋转之后成为了根结点，所以当在该条件时，最终平衡因子一定是0
			subL->_balancefactor = -1;//30  => 旋转之后成为了左子树的根，同理90，要判断谁链接的是h-1+1，谁链接的是h-1
		}
		else if (balancefactor == -1)//同理，如果该结点的平衡因子等于-1，那么此时表示结点插入在该结点的左孩子
		{
			parent->_balancefactor = 1;//90  => 同理上述情况，只是此时反过来了，h-1+1链接到了30的右孩子，h-1链接到了90的左孩子，所以30平衡因子为0,90平衡因子为1
			subLR->_balancefactor = 0;//60
			subL->_balancefactor = 0;//30
		}
		else if (balancefactor == 0)//同理，此时表示的就是左右孩子结点都没有插入数据，但是此时依然会发生左右双旋，但是双旋完之后，30和90因为没有h-1+1和h-1的区别（因为没有插入结点），所以所有的平衡因子都是0
		{                           //也就是当h=0的情况，h-1=-1不存在，也就是相当于是60就是此时的新增结点
			parent->_balancefactor = 0;
			subLR->_balancefactor = 0;
			subL->_balancefactor = 0;//单旋同理，直接全部给0就完事了
		}
		else//直接报警，因为此时旋转完之后，对应结点的平衡因子不为0，-1,1，说明此时该树不是一棵AVL树
		{
			assert(false);//这个表示的是直接断死，因为assert当判断条件为假时就会报警（所以平时我们写代码需要给一个为真的条件，如果不为真，就报警）
			              //并且默认条件和while一样，默认不等于0，所以	此时如果给一个0，就是表示0 != 0，为假，直接报警，反正assert中一定要给一个非0，否则就直接报警
		}
//具体旋转过程：
//           90            进行左单旋           90         然后再进行右单旋         60          完成平衡
//         30  *                              60   *                              30   90
//        *  60                             30  *                                *  *  *  *
//          *  *                           *  *

	}
	void RotateRL(Node* parent)
	{
		Node* subR = parent->_right;
		Node* subRL = subR->_left;
		int balancefactor = subRL->_balancefactor;//天坑代码，一定要在单旋之前就保存住，单旋过后，该结点的平衡因子就不能使用了，因为都是0

		RotateR(parent->_right);
		RotateL(parent);

		if (balancefactor == 1)//同理表示右孩子插入（90的左孩子去链接h-1+1,30的右孩子去链接h-1，导致30的平衡因子变成-1）
		{
			subR->_balancefactor = 0;//90               30   
			subRL->_balancefactor = 0;//60            *    90
			parent->_balancefactor = -1;//30            60 * *
		}                             //               *  *
		else if (balancefactor == -1)//同理，90的左孩子链接h-1,30的右孩子链接h-1+1，最终90的平衡因子变成1
		{
			subR->_balancefactor = 1;//90               30   
			subRL->_balancefactor = 0;//60            *    90
			parent->_balancefactor = 0;//30            60  * *
		}                              //             *  *
		else if (balancefactor == 0)//同理，都不插入，天生就是双旋，此时没有h-1和h+1-1的区别，最终大家的平衡因子都是0
		{
			subR->_balancefactor = 0;//90               30   
			subRL->_balancefactor = 0;//60                 90
			parent->_balancefactor = 0;//30             60
		}
		else
		{
			assert(false);//这个位置出问题了,说明平衡因子没更新对
		}
	}

public:
	void InOrder()//中序打印AVL树
	{
		_InOrder(_root);
		cout << endl;
	}
	void _InOrder(Node* root)
	{
		if (root == nullptr)
		{
			return;
		}
		else
		{
			_InOrder(root->_left);//这边递归不要传参，你真的是人才啊
			cout << root->_kv.first << " ";
			_InOrder(root->_right);
		}
	}
	bool IsBalance()//判断该AVL树是否平衡和平衡因子是否正确
	{
		return _IsBalance(_root);
	}
	int _Height(Node* root)//递归计算子树的高度
	{
		if (root == nullptr)
		{
			return 0;
		}
		//获取到了左子树根结点或者右子树根结点，然后去递归改根结点的左右子树，获取到高度高的那个子树，然后返回，最终把传过来的左子树或者右子树的高度算出来，返回回去
		int leftH = _Height(root->_left);
		int rightH = _Height(root->_right);

		return leftH > rightH ? leftH + 1 : rightH + 1;//让左子树和右子树进行比较，高度高的那个加1（本质就是想返回高度高的那个）
	}
	bool _IsBalance(Node* root)//判断一棵树是否平衡最简单的方法就是判断该树左右结点高度差的绝对值是否小于2（前提是知道子树的高度）
	{
		if (root == nullptr)
		{
			return true;//空树可以认为是一个平衡树
		}
		int leftH = _Height(root->_left);//算出左子树的高度
		int rightH = _Height(root->_right);//算出右子树的高度，目的：算出高度差，然后判断绝对值是否小于等于1

		if (rightH - leftH != root->_balancefactor)//判断平衡因子是否也正确（右子树高度-左子树高度=平衡因子）
		{
			cout << root->_kv.first << "结点平衡因子异常" << endl;
			return false;
		}

		return abs(leftH - rightH) < 2 && _IsBalance(root->_left) && _IsBalance(root->_right);//符合该条件，那么此时就返回1，也就是平衡树，不符合该条件说明此时该树不是平衡树
		//但要明白，不是其中一个子树符合，该树就是AVL树，一定要让整棵树的子树都符合，这棵树才是AVL树，所以需要递归走走判断
		//如下图：
		//          4
		//        2   6
		//      1       15
		//                 16      如此时这个场景，虽然root结点的左右子树符合平衡条件，但是子树并不符合平衡条件，所以想要判断一棵树是否是AVL树，就要让所有的子树去递归判断
	}
private:
	Node* _root;//这边给缺省值参数初始化可以，初始化列表初始化也可以
};
void testAVLtree1()
{
	AVLTree<int, int> t1;
	//int arr[] = { 16,3,7,11,9,26,18,14,15 };
	int arr[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15, 4, 2, 6, 1, 3, 5, 15, 7, 16,14 };//这个只能表明此时这棵树是一个搜索树，不一定是AVL树
	for (auto e : arr)
	{
		t1.Insert(make_pair(e, e));//make_pair接口的作用就是构建一个pair对象，然后返回对应的pair结构体
	    std::cout << "插入" << e << ": " << t1.IsBalance() << endl;
	}

	t1.InOrder();
	std::cout << t1.IsBalance() << endl;
}
void testAVLtree2()
{
	srand(time(0));
	const size_t N = 100000;
	AVLTree<int, int> t;
	for (size_t i = 0; i < N; ++i)
	{
		size_t x = rand();//产生一个随机数，如果想要控制产生的随机数，只需要进行取%就行，例如：想要产生一个[1, 6]之间的随机数，只要使用rand() % 6 + 1的表达式就可以实现
		t.Insert(make_pair(x, x));//任何数%6，得到的都只可能是0到5之间的数（总：摩几得到的就是0到几-1）
	}
	t.InOrder();
	cout << t.IsBalance() << endl;
}

int main()
{
	//testAVLtree1();
	testAVLtree2();

	return 0;
}

总结：同理红黑树，代码不重要，重要的是原理和思路，还有就会画图分析场景的能力