AcWing 904 虫洞

\(AcWing\) \(904\) 虫洞

题目传送门

一、题目描述

农夫约翰在巡视他的众多农场时，发现了很多令人惊叹的虫洞。

虫洞非常奇特，它可以看作是一条 单向 路径，通过它可以使你回到过去的某个时刻（相对于你进入虫洞之前）。

农夫约翰的每个农场中包含 \(N\) 片田地，\(M\) 条路径（双向）以及 \(W\) 个虫洞。

现在农夫约翰希望能够从农场中的某片田地出发，经过一些路径和虫洞回到过去，并在他的出发时刻之前赶到他的出发地。

他希望能够看到出发之前的自己。

请你 判断 一下约翰能否做到这一点。

下面我们将给你提供约翰拥有的农场数量 \(F\)，以及每个农场的完整信息。

已知走过任何一条路径所花费的时间都不超过 \(10000\) 秒，任何虫洞将他带回的时间都不会超过 \(10000\) 秒。

输入格式
第一行包含整数 \(F\)，表示约翰共有 \(F\) 个农场。

对于每个农场，第一行包含三个整数 \(N,M,W\)。

接下来 \(M\) 行，每行包含三个整数 \(S,E,T\)，表示田地 \(S\) 和 \(E\) 之间存在一条路径，经过这条路径所花的时间为 \(T\)。

再接下来 \(W\) 行，每行包含三个整数 \(S,E,T\)，表示存在一条从田地 \(S\) 走到田地 \(E\) 的虫洞，走过这条虫洞，可以回到 \(T\) 秒之前。

输出格式
输出共 \(F\) 行，每行输出一个结果。

如果约翰能够在出发时刻之前回到出发地，则输出 YES，否则输出 NO。

二、知识整理

使用\(spfa\)算法解决是否存在负环问题

求负环的常用方法，基于\(SPFA\)，一般都用方法 \(2\)（该题也是用方法 \(2\)）：

• 方法 \(1\)：统计每个点入队的次数，如果某个点入队\(n\)次，则说明存在负环
• 方法 \(2\)：统计当前每个点的最短路中所包含的边数，如果某点的最短路所包含的边数大于等于\(n\)，则也说明存在环

\(y\)总的原话

每次做一遍\(spfa()\)一定是正确的，但时间复杂度较高，可能会超时。初始时将所有点插入队列中可以按如下方式理解：
在原图的基础上新建一个虚拟源点，从该点向其他所有点连一条权值为\(0\)的有向边。那么原图有负环等价于新图有负环。此时在新图上做\(spfa\)，将虚拟源点加入队列中。然后进行\(spfa\)的第一次迭代，这时会将所有点的距离更新并将所有点插入队列中。执行到这一步，就等价于视频中的做法了。那么视频中的做法可以找到负环，等价于这次\(spfa\)可以找到负环，等价于新图有负环，等价于原图有负环。得证。

• \(1、dist[x]\) 记录虚拟源点到\(x\)的最短距离

• \(2、cnt[x]\) 记录当前\(x\)点到虚拟源点最短路的边数，初始每个点到虚拟源点的距离为\(0\)，只要他能再走\(n\)步，即\(cnt[x] >= n\)，则表示该图中一定存在负环，由于从虚拟源点到\(x\)至少经过\(n\)条边时，则说明图中至少有\(n + 1\)个点，表示一定有点是重复使用

• \(3、\)若\(dist[j] > dist[t] + w[i]\),则表示从\(t\)点走到\(j\)点能够让权值变少，因此进行对该点\(j\)进行更新，并且对应\(cnt[j] = cnt[t] + 1\),往前走一步

注意：该题是判断是否存在负环，并非判断是否存在从\(1\)开始的负环，因此需要将所有的点都加入队列中，更新周围的点

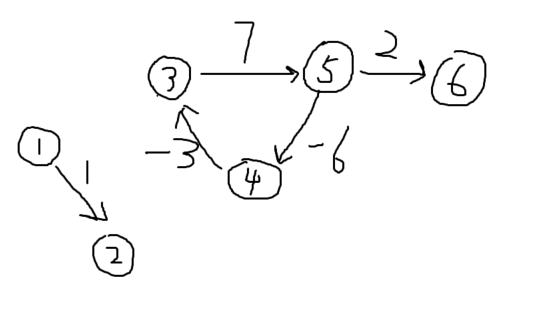
时间复杂度 一般：\(O(m)\) 最坏：\(O(nm)\)

三、实现代码 【心中有超级源点，手中无超级源点】

#include <bits/stdc++.h>
using namespace std;
const int N = 510, M = 5210 * 2;
int n, m1, m2;
int dist[N]; // dist[x]记录源点到x的最短距离
int cnt[N];  // cnt[x]记录源点到x在产生最短距离时的边数
bool st[N];
//邻接表
int e[M], h[N], idx, w[M], ne[M];
void add(int a, int b, int c) {
    e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
}

bool spfa() {
    //初始化距离INF
    memset(dist, 0x3f, sizeof dist);
    //是不是已经加入到集合中
    memset(st, 0, sizeof st);
    //初始化从源点到x的最短距离时，边数都是0
    memset(cnt, 0, sizeof cnt);

    queue<int> q;
    
    //底层相当于有一个虚拟源点0
    // 0到 [1,n]的所有点，边权为0，不影响现在的图
    // 从虚拟节点0出发，到达所有的1~n，就成为了单源最短路径问题
    for (int i = 1; i <= n; i++) q.push(i), st[i] = true;

    // spfa
    while (q.size()) {
        int u = q.front();
        q.pop();
        st[u] = false;

        for (int i = h[u]; ~i; i = ne[i]) {
            int j = e[i];
            if (dist[j] > dist[u] + w[i]) {
                dist[j] = dist[u] + w[i];
                /*
                dist[j]表示j点距离源点的距离，cnt[j]表示从源点到j点经过的边数
                cnt[j] = cnt[u] + 1 的意思是 如果距离更新了，那么从源点到j的边数就等于源点到u的边数 + 1
                所以通过这个我们可以判断是否存在负环，如果在j，u之间存在负环，那么cnt[j] 会不断加1

                我们通过判断cnt[j] >= n  确定是否存在负环

                为什么是cnt[j] >= n ？ 因为cnt数组表示的是边数，如果从某点到j点的边数大于等于n，那么在源点和j点之间肯定存在n+1个点，
                但是最多只有n个点，根据抽屉原理，所以必然有点重复出现，存在负环 ！
                */
                cnt[j] = cnt[u] + 1;
                if (cnt[j] > n) return true;

                if (!st[j]) {
                    q.push(j);
                    st[j] = true;
                }
            }
        }
    }
    return false;
}

int main() {
    int T;
    cin >> T;
    while (T--) {
        cin >> n >> m1 >> m2;
        //初始化邻接表
        memset(h, -1, sizeof h);
        idx = 0;

        int a, b, c;

        //田地 双向边
        while (m1--) {
            cin >> a >> b >> c;
            add(a, b, c), add(b, a, c);
        }

        //虫洞 回到t秒前 单向负边
        while (m2--) {
            cin >> a >> b >> c;
            add(a, b, -c);
        }
        //用spfa判断是不是有负环
        if (spfa())
            cout << "YES" << endl;
        else
            cout << "NO" << endl;
    }
    return 0;
}

四、实现代码 【心中有超级源点，手中也要有超级源点】

不推荐写法

这种实现方式不好，原因如下：

• 需要扩大\(M\)的上限,因为多了\(N\)条边，需要扩大为\(M=M+N\)
• 需要手动把超级源点到各个点的边真正创建出来
• 在判断是否有环时，因为现在是\(N+1\)个点，条件也有一些变化：
  if (cnt[j] > n) return ~ true;
  没有了等号，原因很简单，因为现在是\(n+1\)个点,\(cnt[j]\)记录的是经过的边数量，\(n+1\)个点可以最多有\(n\)条边，只有大于\(n\)才是有负环
  

#include <bits/stdc++.h>
using namespace std;
const int N = 510, M = 5210 + N;
int n, m1, m2;
int dist[N]; // dist[x]记录源点到x的最短距离
int cnt[N];  // cnt[x]记录源点到x在产生最短距离时的边数
bool st[N];
//邻接表
int e[M], h[N], idx, w[M], ne[M];
void add(int a, int b, int c) {
    e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
}

bool spfa() {
    //初始化距离INF
    memset(dist, 0x3f, sizeof dist);
    //是不是已经加入到集合中
    memset(st, 0, sizeof st);
    //初始化从源点到x的最短距离时，边数都是0
    memset(cnt, 0, sizeof cnt);

    queue<int> q;

    //完全按虚拟源点的思想构建，把虚拟原点加到图中，需要M增加N个数据范围，才能保证边数能装的下,事实证明，此题不在原始M上加N，会TLE
    q.push(0), st[0] = true, dist[0] = 0;
    for (int i = 1; i <= n; i++) add(0, i, 0); //虚拟原点->i增加一条边权为0的边

    // spfa
    while (q.size()) {
        int u = q.front();
        q.pop();
        st[u] = false;

        for (int i = h[u]; ~i; i = ne[i]) {
            int j = e[i];
            if (dist[j] > dist[u] + w[i]) {
                dist[j] = dist[u] + w[i];
                /*
                dist[j]表示j点距离源点的距离，cnt[j]表示从源点到j点经过的边数
                cnt[j] = cnt[u] + 1 的意思是 如果距离更新了，那么从源点到j的边数就等于源点到u的边数 + 1
                所以通过这个我们可以判断是否存在负环，如果在j，u之间存在负环，那么cnt[j] 会不断加1

                我们通过判断cnt[j] >n  确定是否存在负环

                为什么是cnt[j] > n ？ 因为cnt数组表示的是边数，如果从某点到j点的边数大于等于n，那么在源点和j点之间肯定存在n+1个点，
                但是最多只有n个点，根据抽屉原理，所以必然有点重复出现，存在负环 ！
                */
                cnt[j] = cnt[u] + 1;
                if (cnt[j] > n) return true;

                if (!st[j]) {
                    q.push(j);
                    st[j] = true;
                }
            }
        }
    }
    return false;
}

int main() {
    int T;
    cin >> T;
    while (T--) {
        cin >> n >> m1 >> m2;
        //初始化邻接表
        memset(h, -1, sizeof h);
        idx = 0;

        int a, b, c;

        //田地 双向边
        while (m1--) {
            cin >> a >> b >> c;
            add(a, b, c), add(b, a, c);
        }

        //虫洞 回到t秒前 单向负边
        while (m2--) {
            cin >> a >> b >> c;
            add(a, b, -c);
        }
        //用spfa判断是不是有负环
        if (spfa())
            cout << "YES" << endl;
        else
            cout << "NO" << endl;
    }
    return 0;
}