提供了编程的基础技术教程

zl程序教程

您现在的位置是：首页 >  其它

当前栏目

GAMES101作业7提高-实现微表面模型你需要了解的知识

实现 模型 了解 需要 知识 提高 作业 表面
2023-09-11 14:22:30 时间

目录

微表面材质模型

微平面理论 Microfacet Theory

BSDF（浅浅的提一下）

微表面BRDF的实现

Cook-Torrance BRDF

漫反射的BRDF

镜面反射的BRDF

1 法线分布函数 D

GGX分布简介

Trowbridge-Reitz 分布(GGX分布) 公式

表面粗糙度​编辑的取值

实现代码

2 阴影遮挡函数 G

Smith遮蔽函数

Disney实现方法

实现代码

 UE4方法-SchlickGGX 

实现代码

3 菲涅尔项 F

实现代码

参考

微表面材质模型

Microfacet Material，也是真实感材质模型，同时是PBR（Physicallly-Based-Rendering 基于物理渲染）基于的东西。

之前作业中涉及到的 BRDF，即Bidirectional Reflectance Distribution Function，双向反射分布函数，微表面模型就是基于物理的BRDF，也是最常用的一种物理BRDF。

微平面理论 Microfacet Theory

下面是我结合课程内容对微平面理论的一些理解。

现实生活中，物体表面都是不规则的，离近了看会有坑坑洼洼的感觉，这就意味着这些坑坑洼洼的小表面反射的光方向都不同。但对于每个小表面来说，入射的光线只会被分为反射光和折射光。基于此，微表面模型假设：①微表面的尺寸小于着色区域大于可见光波长；物体表面从远处看是外观（diffuse、glossy），近处看是一个个微小的、平的几何面，②这些平坦的几何面都符合几何光学定律，可以看成是一个个非常小的镜子；③光线只在微表面之间弹射一次（single-bounce），一次之后弹射的光线不改变着色结果。（关于假设③，这里不考虑下图所示的光线多次弹射的情况，次表面散射技术后面会单独开一贴讲讲）

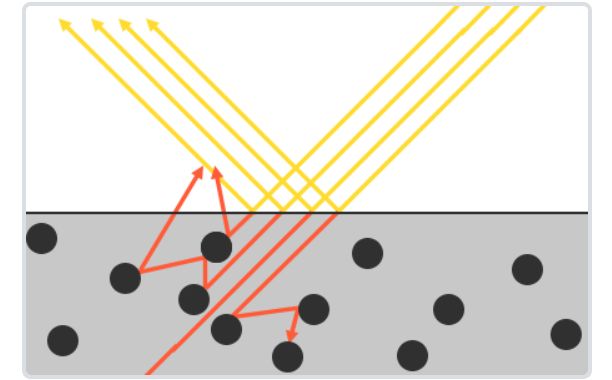
有了这些假设，解微表面材质模型的关键在于：解微表面朝向的分布，具体来说就是微表面的法线分布。如下图，对于两种典型的材质与法线分布的关系：法线集中->glossy；法线发散->diffuse。

 

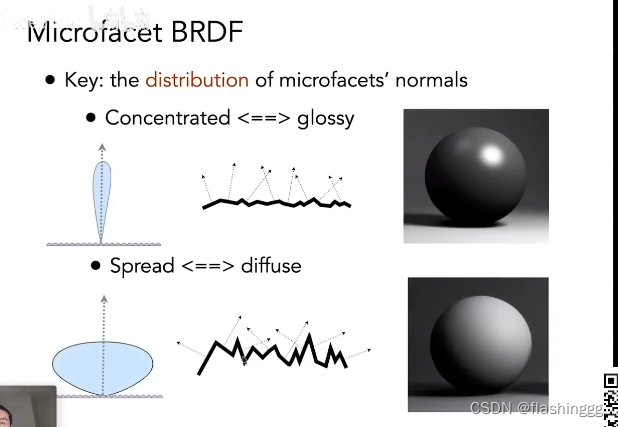
BSDF（浅浅的提一下）

BSDF（Bidirectional Scattering Distribution Function，S表示的就是“散射”），描述了光如何在物体表面散射，反映了光入射和出射强度的对应关系。之前我们涉及到的反射模型BRDF和透射模型BTDF（T指Transmittance，透射）是BSDF分别只限制了反射和透射的模型结果。BSDF本身是BRDF和BTDF综合作用。

微表面BRDF的实现

一般常用Cook-Torrance BRDF来实现Microfacet：

Cook-Torrance BRDF

Cook-TorranceBRDF考虑了微表面的漫反射和镜面反射，公式如下：

f_{r}=k_{d}f_{lambert}+k_{s}f_{cook-torrance}

其中：k_{d}——折射光占入射光比例；

           k_{s}——反射光占入射光比例；

           f_{lambert}——漫反射（diffuse）的BRDF；

          f_{cook-torrance}——镜面反射（specular）的BRDF;

漫反射的BRDF

上面截图均来自GAMES101课程的P17节：P17-GAMES101-现代计算机图形学入门-闫令琪.漫反射diffuse项用来刻画材质的着色，漫反射的BRDF是个常数项，漫反射朝半球方向均匀弹出，由课上老师介绍的推导过程，可以直接写出漫反射的计算式：

f_{lambert}=\frac{\rho }{\pi }

其中， \rho是个Vecotor3f向量，储存了颜色信息。

镜面反射的BRDF

公式如下：

f_{cool-torrance}=\frac{D(\vec{h})F(\vec{h},\vec{i})G(\vec{i},\vec{o})}{4(\vec{i}\cdot \vec{n})(\vec{o}\cdot \vec{n})}

 其中，i为入射方向；o为出射方向；\vec{h}为半角向量（halfway vector)，即二者中间向量；F为菲涅尔项；G为阴影遮挡函数；D为法线分布函数。

值得一提的是，Cook-Torrance BRDF模型的镜面反射项（specular reflection）是根据Torrance-Sparrow BRDF描述的完整各向同性材质反射模型，再将他应用于图形学得到的。这一项值用来刻画材质的高光。

接下来分别对法线分布函数、阴影遮挡系数和菲涅尔项做介绍。

1 法线分布函数 D

首先要明确一点的是，法线分布函数有Phong分布、Beckmann分布、GGX分布（Trowbridge-Reitz 分布），下文中将只结合GGX分布来介绍法线分布函数。

法线分布函数（Normal Distribution Fuction），NDF，记作：D(\vec{h}).关于法线分布函数的定义，How Is The NDF Really Defined? – Nathan Reed’s coding blog中是这么描述的：“NDF statistically describes the microscopic shape of the surface as a distribution of microfacet orientations.”，即：把微表面的形状描述为表面朝向的分布。目前，主流的法线分布函数已经从传统的Blinn-Phong分布和Beckmann分布，发展到更接近真实世界材质外观的GGX分布。

GGX分布简介

简单介绍一下GGX这个符号，GGX我们经常在各种地方看到。其实GGX分布是Walter等人在论文Microfacet Models for Refraction through Rough Surfaces (cornell.edu)

中提到的一个新的微表面分布函数，该函数能够模拟出粗糙表面的透射效果，下图是论文中展示的利用GGX渲染出的一个玻璃球效果图：

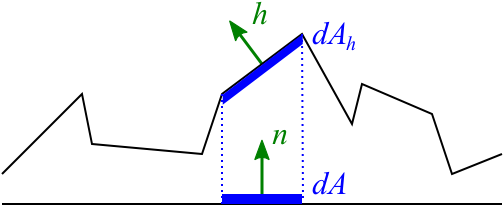
GGX分布是Walter等人的提出的，其认为NDF遵循以下方程：

dA_{h}=D(\vec{h})d\omega_{h}A

其中，A——表示宏观（远处看）表面一小块平的区域；dA_{h}——方向是d\omega _{h}的所有小的平的区域的总面积。

这个公式就可以看出，NDF并不表示密度，而是单位面积、单位立体角的微平面的面积。对上式积分：

\frac{1}{A}\int (\vec{n}\cdot \vec{h})dA_{h}=\int_{\Omega }^{}D(\vec{h})(\vec{n}\cdot \vec{h})d\omega _{h}

其中，(\vec{n}\cdot \vec{h})dA_{h}——微表面投影到宏观表面上的面积；式右边表示正半球立体角的积分，左边表示在所有朝向\vec{h}的微平面面积和，且宏观表面所有方向上的微表面投影面积和等于A。因此式右边应等于1.

\int_{\Omega }^{}D(\vec{h})(\vec{n}\cdot \vec{h})d\omega _{h}=1

此外，GGX分布还有一个限制条件：对于任意观察方向\vec{v}，有：

\int_{\Omega }^{}D(\vec{h})(\vec{v}\cdot \vec{h})d\omega _{h}=\vec{n}\cdot \vec{v}

该式的几何意义如下图：

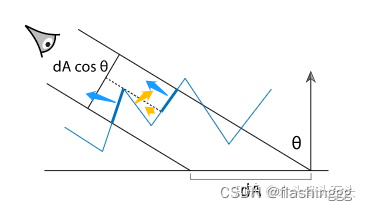
 可以看到，在方向\vec{v}上，要想求在宏观表面上的投影面积，如果如上图所示中朝向为橙色箭头的微表面，求投影后会正负抵消，剩下的就是朝向是蓝色箭头的微表面的投影和。因此投影可以表示为\vec{n}\cdot \vec{v}。

Trowbridge-Reitz 分布(GGX分布) 公式

又称为GGX分布，论文Microfacet Models for Refraction through Rough Surfaces中给的形式为：

D(m)=\frac{\alpha _{g}^{2}\chi ^{+}(m\cdot n)}{\pi cos^{4}\theta _{m}(\alpha _{g}^{2}+tan^{^{2}}\theta _{m})^{2}}

化简后得到可以用于计算的式子：

D(n,h,\alpha )=\frac{\alpha ^{2}}{\pi ((n\cdot h)^{2}(\alpha ^{2}-1)+1)^{2}}

其中： 

\alpha：微表面粗糙度，一般在[0,1]之间，越大越粗糙；

n：宏观表面法向量；

h：微平面法向量，与上文相同，即入射方向和出射方向的中间向量。

表面粗糙度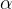\alpha的取值

注意！这里对于微表面粗糙度\alpha的取值，无论是在GGX分布还是在迪士尼用的GTR分布里，都建议将宏观表面粗糙度roughness映射成真正的微表面粗糙度roughness^{2}再进行运算，因此roughness在计算时实际上是4次方。

关于表面粗糙度的取值，参考文章中是这么说的：“在迪士尼原理着色模型Disney principled shading model中，推荐将粗糙度控制以\alpha = r^{2}暴露给用户，其中r是0到1的用户界面粗糙度参数值，可以让GGX分布更线性的方式变化，且这种方式更加实用，不少使用GGX分布的引擎与游戏都采用了这种映射方式。”这里的r表示roughness，粗糙度.

实现代码

float DistributionGGX(float NdotH, float roughness) {
	float a = roughness * roughness;
    float a2 = a * a;
	float pi = 3.1415;
	float m = NdotH * NdotH * (a2 - 1) + 1;

	return a2 / (pi * m * m);//注意分母不能为0，真正使用需要给定一个最小值
}

 了解到这里，已经足够写出GGX密度分布函数的代码了，如果想要深入了解公式如何推到的，可以细看论文中的推导过程。

到这里我们就能理解了：为什么说与Phong和Beckmann相比，GGX更接近真实情况呢？因为GGX可以更好的表现金属高光边缘的消散（拖尾）效果，这里可以参考图形渲染基础：微表面材质模型 - 知乎 (zhihu.com)一文中的解释：

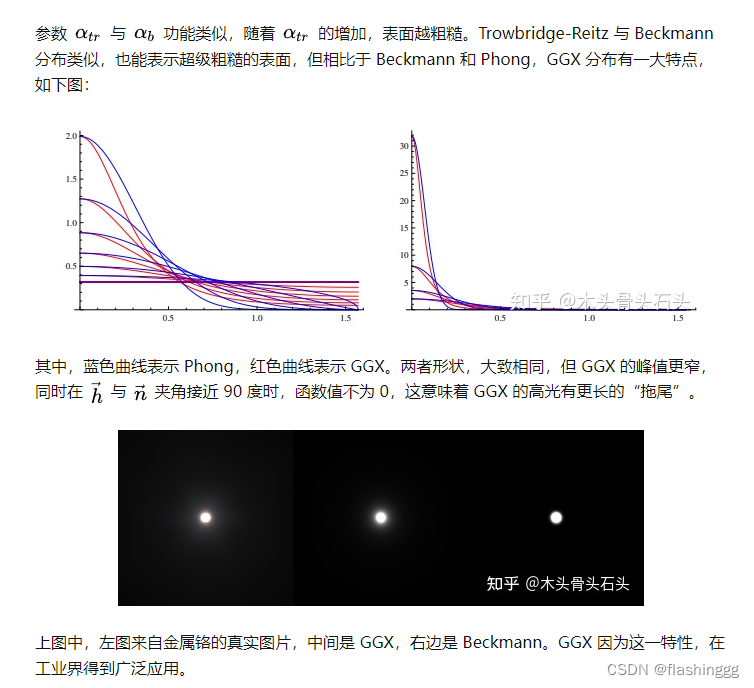
由于GGX的高光有更长的拖尾，因此在表现真实金属表面的时候更胜一筹。

2 阴影遮挡函数 G

微表面是凸凹不平的，从不同观察方向看难免会产生一个表面被另一个表面遮挡的情况（如下图，图源水印）。其中，光照illumination遮挡称为自阴影；从视线viewing看过去被遮挡叫做自遮挡。

BSDF定义了一个几何函数 G 用以模拟微表面由于相互遮挡而导致光线的能量丢失的现象，这个函数就叫做阴影遮挡函数，从定义不难看出，这个函数的取值应该也是从[0,1]的。同时，几何函数有两种形式：

G_{1}——微平面在单个方向（光照方向\vec{l}or视线方向\vec{v}）上可见比例，光照对应遮蔽函数 masking function；视线对应阴影函数 shadowing function.

G_{2}——微平面在光照和视线方向共同可见的比例，称为联合遮蔽阴影函数 joint masking-shadowing function. 

其中，G_{2}由G_{1}推导而来，同时一般微表面材质计算所说的几何函数就是指G_{2}

Smith遮蔽函数

Smith遮蔽函数，即Smith masking function。由于自阴影本质与自遮挡是一样的，都是可见微表面才能对着色有贡献，因此Smith认为二者是相互独立的，有了如下的乘积的Smith Function：

G(\vec{o},\vec{i})=G_{1}(\vec{o})G_{1}(\vec{i})

其中 \vec{o},\vec{i}分别表示入射和出射方向，对应的话就是光源和观察方向。

Smith遮蔽函数对于随机表面的非常准确，但对于一些非随即表面、重复性的图案表现精度会降低（例如面料这种高重复性的结构）。因此在进行布料这种重复性结构图案一般会采用一些专门的shading model去计算。

Disney实现方法

 参考上图， 定义函数G_{1}(\vec{h},\vec{v}),，表示法线方向为\vec{h}的微表面们在观察方向\vec{v}上未被遮挡的比例。根据上述已经讨论过的一个GGX的规定，对于任意观察方向\vec{v}，有：

\int_{\Omega }^{}D(\vec{h})(\vec{v}\cdot \vec{h})d\omega _{h}=\vec{n}\cdot \vec{v}

那么就有：

cos\theta =\int_{\Omega }^{}G_{1}(\vec{h},\vec{v})\cdot max(0,\vec{h}\cdot \vec{v})\cdot D(\vec{h})d\omega _{h}=\vec{n}\cdot \vec{h}

其中，max用来剔除背向观察方向的微表面。

记下来为了简化G_{1}的计算，假设其与微表面朝向无关，可以把它提出来。再通过与视线夹角大于和小于\frac{\pi }{2}的微表面面积和都表现出来，分别命名为A^{+}(\vec{v})和A^{-}(\vec{v})，得到：

G_{1}(\vec{v})=\frac{A^{+}(\vec{v})-A^{-}(\vec{v})}{A^{+}(\vec{v})}

根据该式，结合D(\vec{h})能推导出准确的G_{1}.

G_{GGX}(v)=\frac{2(\vec{n }\cdot \vec{v})}{(\vec{n }\cdot \vec{v})+\sqrt{\alpha ^{2}+(1-\alpha ^{2})(\vec{n }\cdot \vec{v})^{2}}}

其中：\alpha =(0.5+\frac{​{roughness}}{2})^{2}，将粗糙度重映射以减少光泽面的极端增益，使粗糙度变化更加平滑。

实现代码

//对G1的实现
float SmithG_GGX(float NdotV, float roughness) {
	float r = 0.5 + roughness / 2.0f;
	float m = r * r + (1 - r * r) * NdotV * NdotV;

	return 2.0f * NdotV / (NdotV + std::sqrt(m));
}

//光源方向和观察方向分别计算ggx1和ggx2，相乘得到G
float GeometrySmith(Vector3f N, Vector3f V, Vector3f L, float roughness) {
	float NdotV = std::max(dotProduct(N, V), 0.0f);
	float NdotL = std::max(dotProduct(N, L), 0.0f);
	float ggx1 = SmithG_GGX(NdotL, roughness);
	float ggx2 = SmithG_GGX(NdotV, roughness);
	
	return ggx1 * ggx2;
}

 UE4方法-SchlickGGX 

UE4采用的方法是用Schlick近似Smith来计算几何函数，具体怎么算的可以参考这篇文章：

图形学｜PBR：Schlick近似方法 - 知乎 (zhihu.com)

G(\vec{n},\vec{v},\vec{l},k)=G_{sub}(\vec{n},\vec{v},k)G_{sub}(\vec{n},\vec{l},k)

G_{SchlickGGX}(\vec{n},\vec{v},\vec{l},k)=\frac{\vec{n}\cdot \vec{v}}{(\vec{n}\cdot \vec{v})(1-k)+k}

其中：k=\frac{(roughness +1)^{2}}{8}

实现代码

float GeometrySchlickGGX(float NdotV, float roughness) {
	float r = roughness + 1;
	float k = r * r / 8;
	float m = NdotV / NdotV * (1.f - k) + k;
	
	return NdotV / m;
}

//光源方向和观察方向分别计算ggx1和ggx2，相乘得到G
float GeometrySmith(Vector3f N, Vector3f V, Vector3f L, float roughness) {
	float NdotV = std::max(dotProduct(N, V), 0.0f);
	float NdotL = std::max(dotProdoct(N, L), 0.0f);
	float ggx1 = GeometrySchlickGGX(NdotL, roughness);
	float ggx2 = GeometrySchlickGGX(NdotV, roughness);
	
	return ggx1 * ggx2;
}

除了以上两种方法还有其他的，想了解的话可以看看这篇文章：PBR GGX Specular G 几何函数 - 掘金 (juejin.cn)

3 菲涅尔项 F

就是计算反射光占比。对于菲涅尔效应和菲涅尔项的计算在作业5中有介绍，这里就不赘述了，直接贴代码，想要了解的可以移步GAMES101作业5-从头到尾理解代码&Whitted光线追踪_flashinggg的博客

实现代码

这里直接贴出框架中菲涅尔项的计算函数：

    //菲涅尔方程，与作业5相同
    void fresnel(const Vector3f &I, const Vector3f &N, const float &ior, float &kr) const
    {
        float cosi = clamp(-1, 1, dotProduct(I, N));
        float etai = 1, etat = ior;
        if (cosi > 0) {  std::swap(etai, etat); }
        // Compute sini using Snell's law
        float sint = etai / etat * sqrtf(std::max(0.f, 1 - cosi * cosi));
        // Total internal reflection
        if (sint >= 1) {
            kr = 1;
        }
        else {
            float cost = sqrtf(std::max(0.f, 1 - sint * sint));
            cosi = fabsf(cosi);
            float Rs = ((etat * cosi) - (etai * cost)) / ((etat * cosi) + (etai * cost));
            float Rp = ((etai * cosi) - (etat * cost)) / ((etai * cosi) + (etat * cost));
            kr = (Rs * Rs + Rp * Rp) / 2;
        }

看到这里，实现作业7中的微表面材质提高部分就没问题了，会另开一贴介绍具体的实现代码.

以及之后会再总结一下微表面材质学习引出的其他拓展内容，例如PBR除了微表面其他的内容是什么？Disney Principle是什么？等等...

参考

图形渲染基础：微表面材质模型 - 知乎 (zhihu.com)

【基于物理的渲染（PBR）白皮书】（四）法线分布函数相关总结 - 知乎 (zhihu.com)

How Is The NDF Really Defined? – Nathan Reed’s coding blog (reedbeta.comd

基于物理的渲染：微平面理论(Cook-Torrance BRDF推导) - 知乎 (zhihu.com)

相关文章