初等数学基础
函数
0.符号
≥ :> 或 = 。a≥0 ⇦⇨ a>0 或 a=0
[]:取整函数,
x
−
1
<
[
x
]
≤
x
x-1<[x]≤x
x−1<[x]≤x
x 2 = ∣ x ∣ \sqrt{x^2}=|x| x2=∣x∣
例题1:取整函数求极限

思路:①取整函数不等式 + ②夹逼原理

1.函数四性质
1.单调性
证明函数不等式:构造辅助函数 + 单调性
例题1:12年15.
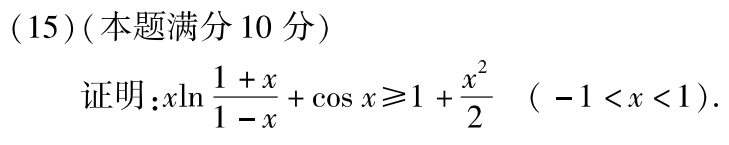
分析:f’‘(x)>0 ∴f’(x)单增 ∴f’(x)>f’(0)=0 ∴f(x)单增 ∴f(x)>f(0)=0
答案:略
2.奇偶性
奇函数: f ( − x ) = − f ( x ) f(-x)=-f(x) f(−x)=−f(x)
若奇函数在x=0处有定义,则 f 奇 ( 0 ) = 0 f_{奇}(0)=0 f奇(0)=0(奇函数的必要条件)
偶函数: f ( − x ) = f ( x ) f(-x)=f(x) f(−x)=f(x)
3.对称性
4.周期性
2.初等函数及其图像
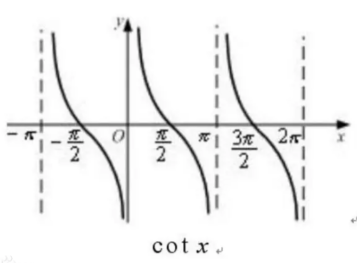
cot x \cot x cotx
余切cotx,是正切tanx的倒数
cot x = 1 tan x \cot x=\dfrac{1}{\tan x} cotx=tanx1
例题:11年4. 定积分的保号性

分析:
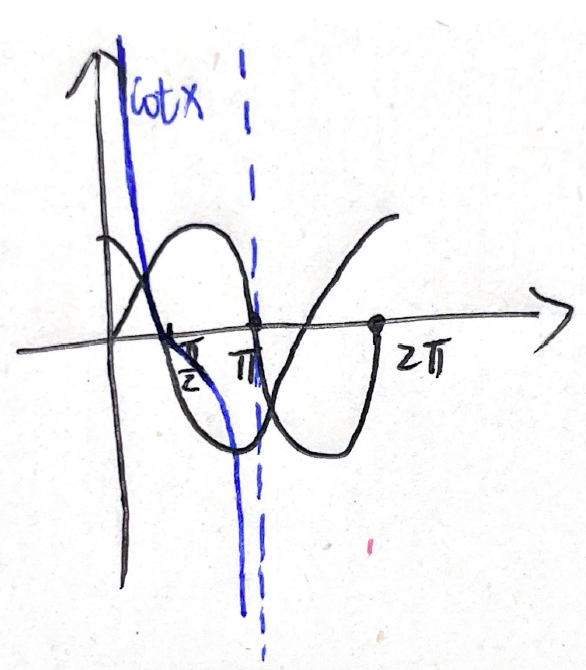
答案:B
sec x \sec x secx
正割secx,是余弦cosx的倒数
1.定义: sec x = 1 cos x \sec x=\dfrac{1}{\cos x} secx=cosx1
2.三角恒等式: sec 2 x = 1 + tan 2 x \sec^2x=1+\tan^2x sec2x=1+tan2x
3.导数: ( sec x ) ′ = sec x tan x (\sec x)'=\sec x\tan x (secx)′=secxtanx
4.积分: ∫ sec x d x = ln ∣ sec x + tan x ∣ + C \int \sec x{\rm d}x=\ln|\sec x+\tan x|+C ∫secxdx=ln∣secx+tanx∣+C
例题:11年9.
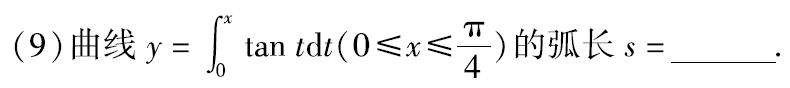
答案: ln ( 1 + 2 ) \ln(1+\sqrt{2}) ln(1+2)
3.三角恒等式
s e c 2 x = 1 + t a n 2 x sec^2x = 1+tan^2x sec2x=1+tan2x
4.三角函数
sin 3 x \sin³x sin3x
sinωt 是以
2
π
ω
\dfrac{2π}{ω}
ω2π为周期的正弦函数,ω越大,周期越小。
例如:sinx周期为2π,sin2x的周期为π
易错点: ∫ 0 2 π s i n 3 t d t = 0 \int_0^{2π}sin^3t{\rm d}t=0 ∫02πsin3tdt=0
∵ω始终为1,∴一个蘑菇的跨度始终为π。只不过sin的偶次方,因为负数部分会翻上来,周期会变成π,奇次方还是和一次方一样
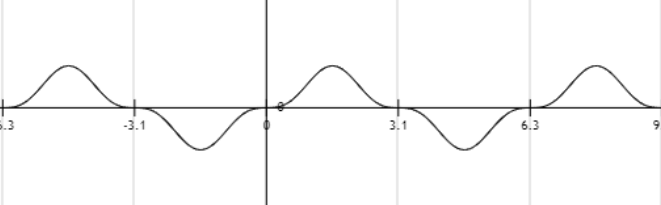
如图, s i n 3 t sin^3t sin3t的图像,和 s i n t sint sint差别不大,只是从饱满变得更加突起
sin 1 x \sin\dfrac{1}{x} sinx1
y
=
s
i
n
1
x
y=sin\dfrac{1}{x}
y=sinx1图像
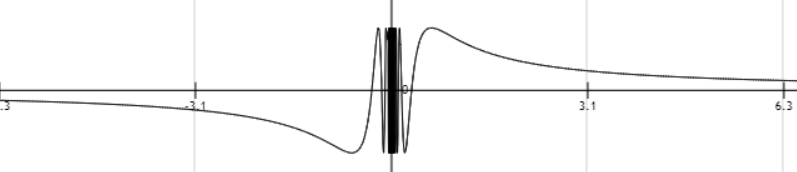
由
y
=
s
i
n
1
x
y=sin\dfrac{1}{x}
y=sinx1图像可知,
y
=
s
i
n
1
x
y=sin\dfrac{1}{x}
y=sinx1在x=0处是有界振荡,不存在无穷间断点,故没有铅直渐近线。
公式
1.一元二次方程求根公式
一元二次方程 a x 2 + b x + c = 0 ax²+bx+c = 0 ax2+bx+c=0 的解为 x = − b ± b 2 − 4 a c 2 a x = \dfrac{-b±\sqrt{b²-4ac}}{2a} x=2a−b±b2−4ac
1.诱导公式
cos
k
π
=
(
−
1
)
k
\cos kπ=(-1)^k
coskπ=(−1)k
t
a
n
(
π
2
−
α
)
=
c
o
t
α
=
1
t
a
n
α
tan(\dfrac{π}{2}-α)=cotα=\dfrac{1}{tanα}
tan(2π−α)=cotα=tanα1
2.韦达定理
设一元二次方程
a
x
2
+
b
x
+
c
=
0
(
a
,
b
,
c
∈
R
,
a
≠
0
)
ax^2+bx+c=0(a,b,c∈R,a≠0)
ax2+bx+c=0(a,b,c∈R,a=0)中,两根x₁、x₂有如下关系:
x
1
+
x
2
=
−
b
a
x_1+x_2=-\dfrac{b}{a}
x1+x2=−ab
x 1 x 2 = c a x_1x_2=\dfrac{c}{a} x1x2=ac
在求解微分方程的特征方程时,经常会用到韦达定理。
二阶线性微分方程
y
′
′
+
p
y
′
+
q
y
=
0
y''+py'+qy=0
y′′+py′+qy=0 的特征方程为
λ
2
+
p
λ
+
q
=
0
λ^2+pλ+q=0
λ2+pλ+q=0,则
λ
1
+
λ
2
=
−
p
1
=
−
p
λ_1+λ_2=-\dfrac{p}{1}=-p
λ1+λ2=−1p=−p
λ
1
⋅
λ
2
=
q
1
=
q
λ_1·λ_2=\dfrac{q}{1}=q
λ1⋅λ2=1q=q
通过二阶齐次微分方程的通解形式,可以直接知道 λ 1 、 λ 2 λ_1、λ_2 λ1、λ2的取值。(见高数下二阶齐次的表格)

3.平方公式
三和平方: ( x + y + z ) 2 = x 2 + y 2 + z 2 + 2 x y + 2 y z + 2 x z (x+y+z)²=x²+y²+z²+2xy+2yz+2xz (x+y+z)2=x2+y2+z2+2xy+2yz+2xz
(
x
+
y
+
z
)
2
=
x
2
+
y
2
+
z
2
+
2
x
y
+
2
y
z
+
2
x
z
(x+y+z)²=x²+y²+z²+2xy+2yz+2xz
(x+y+z)2=x2+y2+z2+2xy+2yz+2xz
即
(
x
y
+
y
z
+
x
z
)
=
1
2
[
(
x
+
y
+
z
)
2
−
(
x
2
+
y
2
+
z
2
)
]
(xy+yz+xz)=\dfrac{1}{2}[(x+y+z)²-(x²+y²+z²)]
(xy+yz+xz)=21[(x+y+z)2−(x2+y2+z2)]
例题:18年12. 轮换对称性
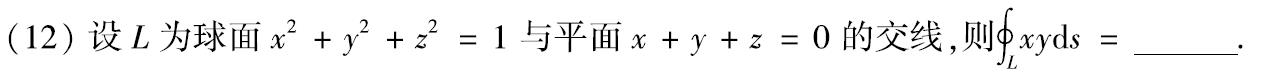
分析:轮换对称性、可代入、三和平方公式
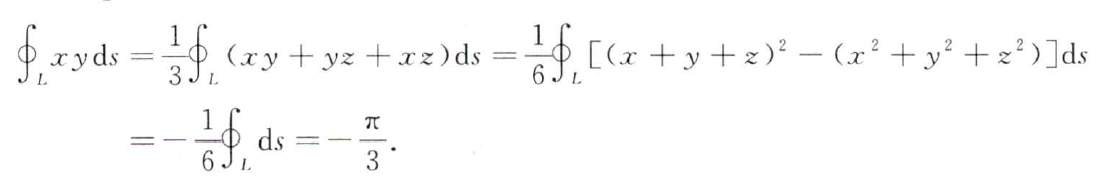
答案: − π 3 -\dfrac{π}{3} −3π
4.立方公式
立方和公式
a 3 + b 3 = ( a + b ) ( a 2 − a b + b 2 ) a^3+b^3=(a+b)(a^2-ab+b^2) a3+b3=(a+b)(a2−ab+b2)
立方差公式
a 3 − b 3 = ( a − b ) ( a 2 + a b + b 2 ) a^3-b^3=(a-b)(a^2+ab+b^2) a3−b3=(a−b)(a2+ab+b2)
完全立方公式
( a + b ) 3 = a 3 + 3 a 2 b + 3 a b 2 + b 3 (a+b)^3=a^3+3a^2b+3ab^2+b^3 (a+b)3=a3+3a2b+3ab2+b3
令b=-b,则b3=-b3
(
a
−
b
)
3
=
a
3
−
3
a
2
b
+
3
a
b
2
−
b
3
(a-b)^3=a^3-3a^2b+3ab^2-b^3
(a−b)3=a3−3a2b+3ab2−b3
例题:08年5. 幂零阵、可逆矩阵定义、立方和公式、立方差公式

分析:由 A 3 = O A³=O A3=O得 E ± A 3 = E E±A^3=E E±A3=E
即 E = E + A 3 = ( E + A ) ( E 2 − A E + A 2 ) = ( E + A ) ( E − A + A 2 ) E=E+A^3=(E+A)(E^2-AE+A^2)=(E+A)(E-A+A²) E=E+A3=(E+A)(E2−AE+A2)=(E+A)(E−A+A2),则 E + A E+A E+A可逆且 ( E + A ) − 1 = E − A + A 2 (E+A)^{-1}=E-A+A² (E+A)−1=E−A+A2
即 E = E − A 3 = ( E − A ) ( E 2 + A E + A 2 ) = ( E − A ) ( E + A + A 2 ) E=E-A^3=(E-A)(E^2+AE+A^2)=(E-A)(E+A+A^2) E=E−A3=(E−A)(E2+AE+A2)=(E−A)(E+A+A2),则 E − A E-A E−A可逆且 ( E − A ) − 1 = E + A + A 2 (E-A)^{-1}=E+A+A^2 (E−A)−1=E+A+A2
答案:C
5.解析几何
边长为a的正三角的面积 S = 3 4 a 2 S=\dfrac{\sqrt{3}}{4}a² S=43a2
设正三角形的边长为a,则高 h = 3 2 a h=\dfrac{\sqrt{3}}{2}a h=23a,面积 S = 3 4 a 2 S=\dfrac{\sqrt{3}}{4}a² S=43a2
例题:07年14. 关于坐标面的对称性、轮换对称性
分析:
∣
x
∣
+
∣
y
∣
+
∣
z
∣
=
1
|x|+|y|+|z|=1
∣x∣+∣y∣+∣z∣=1 是正八面体 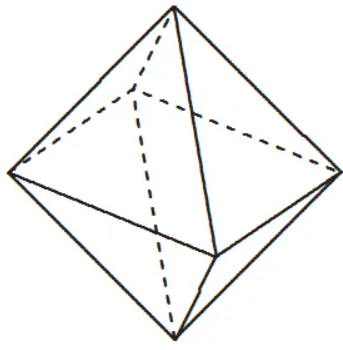 。
。
考虑曲面Σ关于yOz平面对称,则关于x的奇函数的曲面积分为0,即
∯
Σ
x
d
S
=
0
\oiint\limits_Σx\ {\rm d}S=0
Σ∬x dS=0
∴
∯
Σ
(
x
+
∣
y
∣
)
d
S
=
∯
Σ
∣
y
∣
d
S
=
轮换对称性
1
3
∯
Σ
(
∣
x
∣
+
∣
y
∣
+
∣
z
∣
)
d
S
=
1
3
∯
Σ
d
S
\oiint\limits_Σ(x+|y|)\ {\rm d}S=\oiint\limits_Σ|y|\ {\rm d}S\xlongequal{轮换对称性}\dfrac{1}{3}\oiint\limits_Σ(|x|+|y|+|z|)\ {\rm d}S=\dfrac{1}{3}\oiint\limits_Σ{\rm d}S
Σ∬(x+∣y∣) dS=Σ∬∣y∣ dS轮换对称性31Σ∬(∣x∣+∣y∣+∣z∣) dS=31Σ∬dS
观察该正八面体 ∣ x ∣ + ∣ y ∣ + ∣ z ∣ = 1 |x|+|y|+|z|=1 ∣x∣+∣y∣+∣z∣=1,其在第一卦限上的表面积为一个正三角形,边长为 2 \sqrt{2} 2,则正三角形的面积为 3 4 a 2 = 3 4 × 2 = 3 2 \dfrac{\sqrt{3}}{4}a²=\dfrac{\sqrt{3}}{4}×2=\dfrac{\sqrt{3}}{2} 43a2=43×2=23
则 1 3 ∯ Σ d S = 1 3 × 8 × 3 2 = 4 3 3 \dfrac{1}{3}\oiint\limits_Σ{\rm d}S=\dfrac{1}{3}×8×\dfrac{\sqrt{3}}{2}=\dfrac{4\sqrt{3}}{3} 31Σ∬dS=31×8×23=343

答案: 4 3 3 \dfrac{4\sqrt{3}}{3} 343
6.等比数列求和公式
S n = a 1 ( 1 − q n ) 1 − q ( q ≠ 1 ) S_n=\dfrac{a_1(1-q^n)}{1-q} \qquad \qquad (q≠1) Sn=1−qa1(1−qn)(q=1)
推导:
①q=1时:
S
n
=
n
a
1
S_n=na_1
Sn=na1
②q≠1时:
a
n
+
1
=
q
a
n
=
a
1
q
n
a_{n+1}=qa_n=a_1q^n
an+1=qan=a1qn
S
n
=
a
1
+
a
2
+
.
.
.
+
a
n
S_n=a_1+a_2+...+a_n
Sn=a1+a2+...+an
q
S
n
=
q
a
1
+
q
a
2
+
.
.
.
+
q
a
n
=
a
2
+
a
3
+
.
.
.
+
a
n
+
1
qS_n=qa_1+qa_2+...+qa_n=a_2+a_3+...+a_{n+1}
qSn=qa1+qa2+...+qan=a2+a3+...+an+1
∴
S
n
−
q
S
n
=
a
1
−
a
n
+
1
∴S_n-qS_n=a_1-a_{n+1}
∴Sn−qSn=a1−an+1
即
(
1
−
q
)
S
n
=
a
1
−
a
n
+
1
(1-q)S_n=a_1-a_{n+1}
(1−q)Sn=a1−an+1
∴
S
n
=
a
1
−
a
n
+
1
1
−
q
=
a
1
(
1
−
q
n
)
1
−
q
∴S_n=\dfrac{a_1-a_{n+1}}{1-q}=\dfrac{a_1(1-q^{n})}{1-q}
∴Sn=1−qa1−an+1=1−qa1(1−qn)
7.取整符号 [ ]
[a]表示不超过a的最大整数
例题1:05年15.
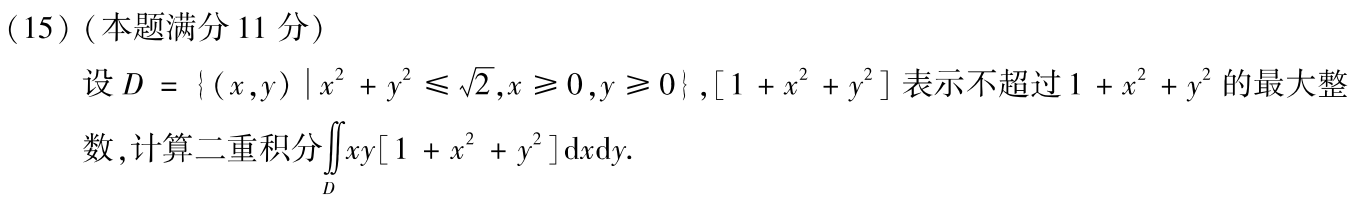
分析:[1+x²+y²]表示不超过1+x²+y²的最大整数

答案: 3 8 \dfrac{3}{8} 83

