高数(下) 第十二章:无穷级数
文章目录
Ch12. 无穷级数
一、常数项级数
(一)正项级数
(二)交错级数
(三)任意项级数
1.四个特殊的常数项级数
①等比级数
等比级数(几何级数): ∑ i = 0 ∞ a q i = { a 1 − q ( 收敛 ) , ∣ q ∣ < 1 ∞ ( 发散 ) , ∣ q ∣ ≥ 1 \sum\limits_{i=0}^∞aq^i=\left\{\begin{aligned} \dfrac{a}{1-q}\ (收敛),& |q|<1\\ ∞\ (发散),& |q|≥1 \end{aligned}\right. i=0∑∞aqi=⎩ ⎨ ⎧1−qa (收敛),∞ (发散),∣q∣<1∣q∣≥1
②p级数
p级数: ∑ n = 1 ∞ 1 n p \sum\limits_{n=1}^∞\dfrac{1}{n^p} n=1∑∞np1 { p > 1 , 收敛 0 < p ≤ 1 , 发散 \left\{\begin{aligned} p>1 ,& 收敛\\ 0<p≤1 ,& 发散 \end{aligned}\right. {p>1,0<p≤1,收敛发散
p=2>1时, ∑ n = 1 ∞ 1 n 2 = π 2 6 \sum\limits_{n=1}^∞\dfrac{1}{n^2}=\dfrac{π^2}{6} n=1∑∞n21=6π2
③调和级数
调和级数: ∑ n = 1 ∞ 1 n = 1 + 1 2 + 1 3 + . . . + 1 n + . . . = ∞ \sum\limits_{n=1}^∞\dfrac{1}{n}=1+\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{n}+...=∞ n=1∑∞n1=1+21+31+...+n1+...=∞ 发散
④交错调和级数、交错p级数
交错调和级数: ∑ n = 1 ∞ ( − 1 ) n − 1 1 n = 1 − 1 2 + 1 3 + . . . + ( − 1 ) n − 1 1 n + . . . = ln 2 \sum\limits_{n=1}^∞(-1)^{n-1}\dfrac{1}{n}=1-\dfrac{1}{2}+\dfrac{1}{3}+...+(-1)^{n-1}\dfrac{1}{n}+...=\ln2 n=1∑∞(−1)n−1n1=1−21+31+...+(−1)n−1n1+...=ln2 收敛
交错p级数: ∑ n = 1 ∞ ( − 1 ) n − 1 1 n p \sum\limits_{n=1}^∞(-1)^{n-1}\dfrac{1}{n^p} n=1∑∞(−1)n−1np1 { p > 1 , 绝对收敛 0 < p ≤ 1 , 条件收敛 \left\{\begin{aligned} p>1, & 绝对收敛 \\ 0<p≤1, & 条件收敛 \end{aligned}\right. {p>1,0<p≤1,绝对收敛条件收敛
2.收敛级数的性质(针对任意项级数)
(1)(2)加减数乘都收敛
例题:06年9.

分析:ABC仅对正项级数成立。
举反例:
AB:
a
n
=
(
−
1
)
n
⋅
1
n
a_n=(-1)^n·\dfrac{1}{n}
an=(−1)n⋅n1
C:
a
n
=
(
−
1
)
n
⋅
1
n
a_n=(-1)^n·\dfrac{1}{\sqrt{n}}
an=(−1)n⋅n1
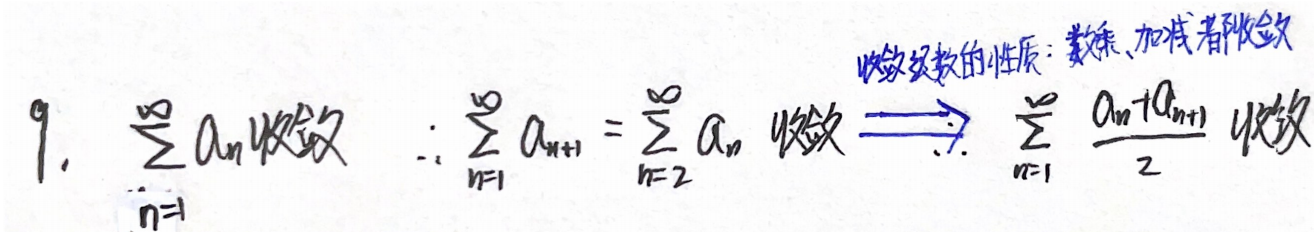
答案:D
3.常数项级数的审敛法
1.正项级数审敛法(判别法)
(1)比较判别法
1.比较审敛法:大的收敛,小的收敛;小的发散,大的发散。
2.比较审敛法可用于抽象级数的审敛。而极限审敛法、比值法、根值法 必须要有具体的级数表达式才能使用。
结论:抽象级数的审敛,仅能使用比较审敛法。关键是要找到比较的对象。
例题1:09年4. 举反例、正项级数的比较审敛法

分析:
对于A,取
a
n
=
b
n
=
(
−
1
)
n
1
n
a_n=b_n=(-1)^n\dfrac{1}{\sqrt{n}}
an=bn=(−1)nn1,则
a
n
b
n
=
1
n
a_nb_n=\dfrac{1}{n}
anbn=n1,为调和级数,发散
对于C,用正项级数的比较审敛法证明C正确:
lim
n
→
∞
a
n
2
b
n
2
∣
b
n
∣
=
lim
n
→
∞
a
n
2
∣
b
n
∣
=
0
∴
∣
b
n
∣
\lim\limits_{n→∞}\dfrac{a_n^2b_n^2}{|b_n|}=\lim\limits_{n→∞}a_n^2|b_n|=0 \quad ∴|b_n|
n→∞lim∣bn∣an2bn2=n→∞liman2∣bn∣=0∴∣bn∣更大。由比较审敛法,大的收敛,则小的
a
n
2
b
n
2
a_n^2b_n^2
an2bn2必收敛

答案:C
(2)比较审敛法极限形式
(3)比值法
ρ = lim n → ∞ u n + 1 ( x ) u n ( x ) { ρ < 1 ,收敛 ρ > 1 ,发散 ρ = 1 ,不定,可能收敛可能发散 ρ=\lim\limits_{n→∞}\dfrac{u_{n+1}(x)}{u_n(x)} \qquad \qquad \left\{\begin{aligned} ρ & < 1,收敛 \\ ρ & > 1,发散 \\ ρ & =1,不定,可能收敛可能发散 \end{aligned}\right. ρ=n→∞limun(x)un+1(x)⎩ ⎨ ⎧ρρρ<1,收敛>1,发散=1,不定,可能收敛可能发散
例题1:22年14.

分析:

答案:-1
(4)根值法
(5)级数收敛的必要条件
级数收敛的必要条件:一般项 u n u_n un趋于零,即 lim n → ∞ u n = 0 \lim\limits_{n→∞}u_n=0 n→∞limun=0
(6)正项级数收敛的充分必要条件
正项级数收敛的充分必要条件:它的部分和数列
s
n
{s_n}
sn有界
即:若
∑
n
=
1
∞
u
n
\sum\limits_{n=1}^∞u_n
n=1∑∞un为正项级数且收敛,则
lim
n
→
∞
S
n
\lim\limits_{n→∞}S_n
n→∞limSn存在
若正项级数
∑
n
=
1
∞
u
n
\sum\limits_{n=1}^∞u_n
n=1∑∞un发散,则
lim
n
→
∞
S
n
\lim\limits_{n→∞}S_n
n→∞limSn不存在
(7)绝对收敛必收敛 (任意项级数)
收敛分绝对收敛和条件收敛: ∑ n = 1 ∞ u n \sum\limits_{n=1}^∞u_n n=1∑∞un绝对收敛 ⇦⇨ ∑ n = 1 ∞ u n \sum\limits_{n=1}^∞u_n n=1∑∞un收敛 且 ∑ n = 1 ∞ ∣ u n ∣ \sum\limits_{n=1}^∞|u_n| n=1∑∞∣un∣也收敛
(8)极限审敛法
(9)积分判别法
(10)A-D判别法(任意项级数)
2.交错级数审敛法 —— 莱布尼茨收敛定理
莱布尼茨收敛定理:
若交错级数
∑
n
=
1
∞
(
−
1
)
n
−
1
u
n
\sum_{n=1}^∞(-1)^{n-1}u_n
∑n=1∞(−1)n−1un 满足
u
n
u_n
un单调递减趋于0,则交错级数收敛
即满足 (1)
u
n
≥
u
n
+
1
u_n≥u_{n+1}
un≥un+1 (2)
lim
n
→
∞
u
n
=
0
\lim\limits_{n→∞}u_n=0
n→∞limun=0.
例题:11年2.

分析:显然
∑
n
=
1
∞
a
n
(
x
−
1
)
n
\sum\limits_{n=1}^∞a_n(x-1)^n
n=1∑∞an(x−1)n 的收敛中心为 x=1,故排除AB
代入x=2,得发散,所以2处应该为开区间,选C
答案:C
3.收敛的分类:绝对收敛与条件收敛
绝对收敛:
∑
n
=
1
∞
u
n
收敛,
∑
n
=
1
∞
∣
u
n
∣
也收敛
绝对收敛:\sum\limits_{n=1}^∞u_n收敛,\sum\limits_{n=1}^∞|u_n|也收敛
绝对收敛:n=1∑∞un收敛,n=1∑∞∣un∣也收敛(本身收敛,各项加绝对值也收敛)
条件收敛:
∑
n
=
1
∞
u
n
收敛,
∑
n
=
1
∞
∣
u
n
∣
发散
条件收敛:\sum\limits_{n=1}^∞u_n收敛,\sum\limits_{n=1}^∞|u_n|发散
条件收敛:n=1∑∞un收敛,n=1∑∞∣un∣发散(本身收敛,各项加绝对值发散)
1.级数共有绝对收敛、条件收敛和发散三种情况。收敛级数只有绝对收敛和条件收敛两种情况。
2.
∑
n
=
1
∞
a
n
x
n
在
x
=
x
0
处条件收敛,则收敛半径
R
=
x
0
\sum\limits_{n=1}^∞a_nx_n在x=x_0处条件收敛,则收敛半径R=x_0
n=1∑∞anxn在x=x0处条件收敛,则收敛半径R=x0
4.常用于举反例的一般项
a n = 1 n a_n=\dfrac{1}{n} an=n1 或 a n = ( − 1 ) n ⋅ 1 n a_n=(-1)^n·\dfrac{1}{n} an=(−1)n⋅n1
a n = ( − 1 ) n ⋅ 1 n a_n=(-1)^n·\dfrac{1}{\sqrt{n}} an=(−1)n⋅n1
二、函数项级数
(二)幂级数
幂级数定义: ∑ n = 0 ∞ a n x n = a 0 + a 1 x + a 2 x 2 2 + a 3 x 3 + . . . + a n x n + . . . \sum\limits_{n=0}^∞a_nx^n=a_0+a_1x+a_2x^22+a_3x^3+...+a_nx^n+... n=0∑∞anxn=a0+a1x+a2x22+a3x3+...+anxn+...
例题1:10年14. 数字特征与幂级数
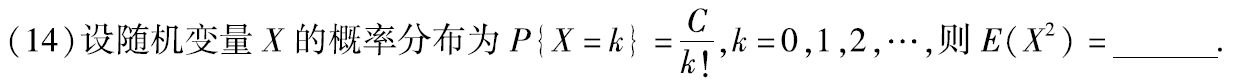
答案:2
1.阿贝尔定理


阿贝尔定理推论1
当|x|<R时,幂级数绝对收敛;
当|x|>R时,幂级数发散;
当x = R或x = -R时,幂级数敛散性不定,可能收敛也可能发散.
正数R称为幂级数的收敛半径。开区间(-R,R)称为幂级数的收敛区间。

阿贝尔定理推论2:条件收敛可得收敛半径
若 ∑ n = 0 ∞ a n x n 在 x = x 0 处条件收敛,则收敛半径 R = x 0 \sum\limits_{n=0}^∞a_nx^n在x=x_0处条件收敛,则收敛半径R=x_0 n=0∑∞anxn在x=x0处条件收敛,则收敛半径R=x0
证明:由Abel定理,
①
∑
n
=
0
∞
a
n
x
n
在
x
=
x
0
\sum\limits_{n=0}^∞a_nx^n在x=x_0
n=0∑∞anxn在x=x0处收敛,则
∣
x
∣
<
∣
x
0
∣
|x|<|x_0|
∣x∣<∣x0∣的一切x使得幂级数绝对收敛,即
R
≥
x
0
R≥x_0
R≥x0。
②若 R = x 0 + ε R=x_0+ε R=x0+ε,则 ∣ x ∣ < ∣ x 0 + ε ∣ |x|<|x_0+ε| ∣x∣<∣x0+ε∣的一切x使得幂级数绝对收敛,即 x = x 0 < x 0 + ε x=x_0<x_0+ε x=x0<x0+ε处绝对收敛。这与 ∑ n = 0 ∞ a n x n 在 x = x 0 \sum\limits_{n=0}^∞a_nx^n在x=x_0 n=0∑∞anxn在x=x0处条件收敛相矛盾,故 R ≤ x 0 R≤x_0 R≤x0
综上①②,收敛半径 R = x 0 R=x_0 R=x0
例题1:15年3.(好题)
2.泰勒级数(麦克劳林级数)
1 + x + x 2 + x 3 + . . . + x n + . . . = 1 1 − x = ∑ n = 0 ∞ x n ( − 1 < x < 1 ) 1 − x + x 2 − x 3 + . . . + ( − 1 ) n x n + . . . = 1 1 + x = ∑ n = 0 ∞ ( − 1 ) n x n ( − 1 < x < 1 ) e x = ∑ n = 0 ∞ 1 n ! x n ( − ∞ < x < + ∞ ) 1+x+x²+x³+...+x^n+...=\dfrac{1}{1-x}=\sum\limits_{n=0}^∞x^n \qquad (-1<x<1)\\[5mm] 1-x+x^2-x^3+...+(-1)^nx^n+...=\dfrac{1}{1+x}=\sum\limits_{n=0}^∞(-1)^nx^n \qquad (-1<x<1)\\[5mm] e^x=\sum\limits_{n=0}^∞\dfrac{1}{n!}x^n \qquad (-∞<x<+∞) 1+x+x2+x3+...+xn+...=1−x1=n=0∑∞xn(−1<x<1)1−x+x2−x3+...+(−1)nxn+...=1+x1=n=0∑∞(−1)nxn(−1<x<1)ex=n=0∑∞n!1xn(−∞<x<+∞)
e x = ∑ k = 0 ∞ x k k ! e^x=\sum\limits_{k=0}^∞\dfrac{x^k}{k!} ex=k=0∑∞k!xk
∴ e = ∑ k = 0 ∞ 1 k ! = lim x → ∞ ( 1 + 1 x ) x ∴e=\sum\limits_{k=0}^∞\dfrac{1}{k!}=\lim\limits_{x→∞}(1+\dfrac{1}{x})^x ∴e=k=0∑∞k!1=x→∞lim(1+x1)x
3.求幂级数的收敛半径、收敛区间、收敛域
1.收敛半径R:
ρ
=
lim
n
→
∞
∣
a
n
+
1
a
n
∣
R
=
1
ρ
ρ=\lim\limits_{n→∞}|\dfrac{a_{n+1}}{a_n}|\qquad \qquad R=\dfrac{1}{ρ}
ρ=n→∞lim∣anan+1∣R=ρ1
2.收敛区间:
(
−
R
,
R
)
(-R,R)
(−R,R) 收敛区间是开区间
3.收敛域:在收敛区间的基础上,验证x=R和x=-R两个端点

用比值法求幂级数的收敛域
u n ( x ) = a n x n , ρ = lim n → ∞ ∣ u n + 1 ( x ) u n ( x ) ∣ < 1 ,收敛 u_n(x)=a_nx^n,ρ=\lim\limits_{n→∞}|\dfrac{u_{n+1}(x)}{u_n(x)}|<1,收敛 un(x)=anxn,ρ=n→∞lim∣un(x)un+1(x)∣<1,收敛
例题1:22年14.
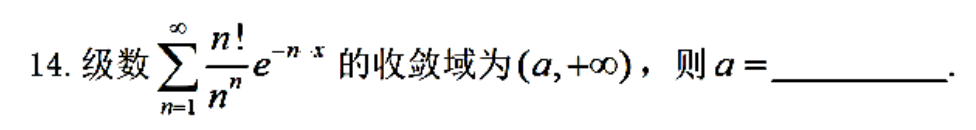
分析: e − n x e^{-nx} e−nx,无法完全分离出 a n a_n an,不能使用阿达玛公式,改用比值法(ρ<1)求x的收敛范围
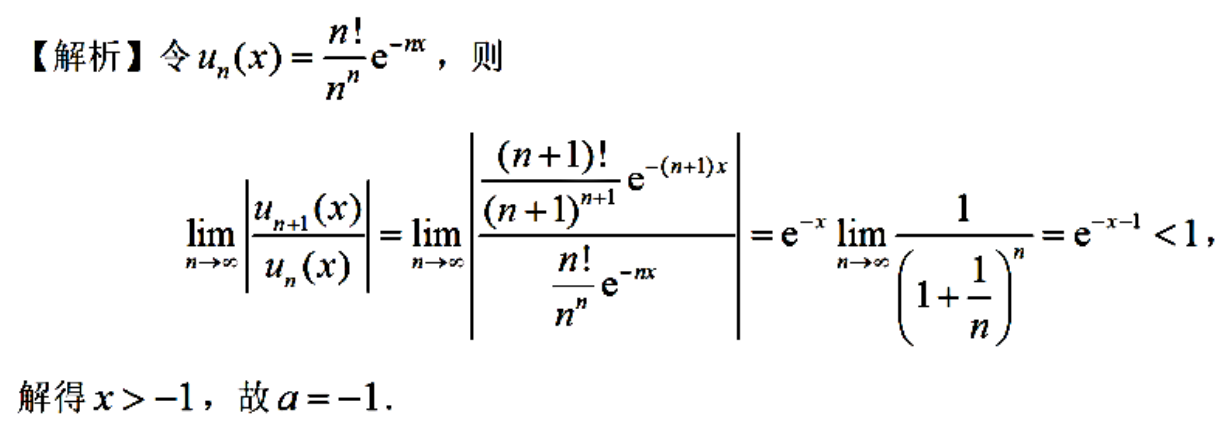
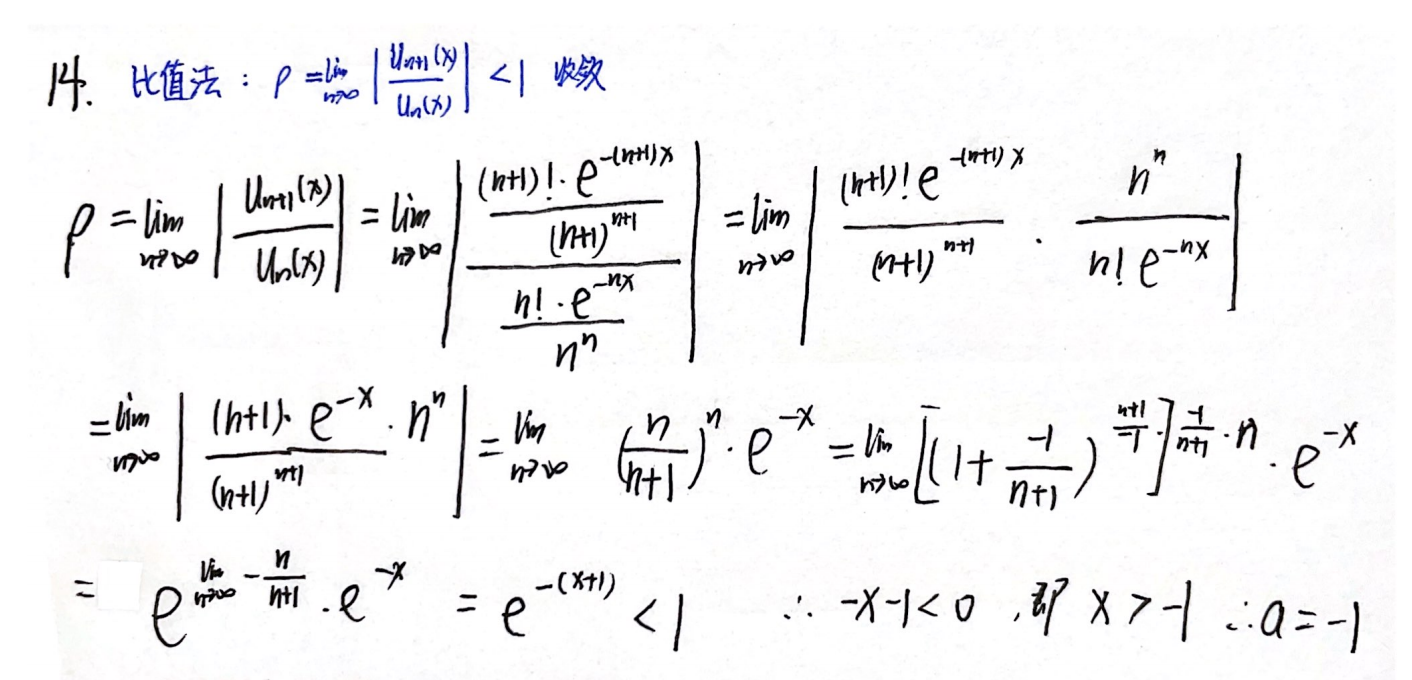
答案:-1
缺项幂级数
缺项幂级数求收敛域: u n ( x ) u_n(x) un(x)比值法,ρ(x)<1,得出收敛区间。再代入端点值验证,得出收敛域。
记 u n ( x ) = a n x n , ρ = lim n → ∞ ∣ u n + 1 ( x ) u n ( x ) ∣ u_n(x)=a_nx^n,ρ=\lim\limits_{n→∞}|\dfrac{u_{n+1}(x)}{u_n(x)}| un(x)=anxn,ρ=n→∞lim∣un(x)un+1(x)∣
例题1:12年17. 缺项幂级数
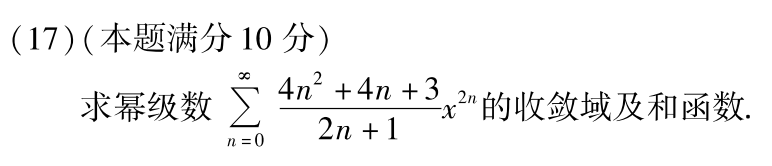
分析:缺项幂级数求收敛域: u n ( x ) u_n(x) un(x)比值法,ρ(x)<1,得出收敛区间。再代入端点值验证,得出收敛域。
答案:

偏心幂级数
4.函数→幂级数 :函数 f ( x ) f(x) f(x)展开为幂级数
函数→幂级数:
①凑标杆:先求导或积分到标杆
1
1
−
x
\dfrac{1}{1-x}
1−x1 的形式 (x可以为任意形式),以“标杆”为桥梁变成幂级数
∑
n
=
0
∞
x
n
\sum\limits_{n=0}^{∞}x^n
n=0∑∞xn (x可以为任意形式)。
②凑题干:和分两项,尽力合并,注意题干是n=0还是n=1,努力把两项变一项,凑成题干的形式
③求常数项级数:此时的求常数项级数,就是把幂级数中的x代入特定值。
例题1:01年13.
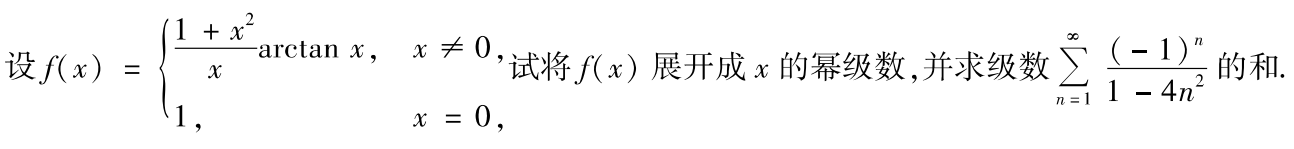
分析:

答案: π 4 − 1 2 \dfrac{π}{4}-\dfrac{1}{2} 4π−21
5.幂级数→函数:求幂级数的和函数S(x)
标杆
(1)重要“标杆”:
∑
n
=
0
∞
x
n
=
1
+
x
+
x
2
+
x
3
+
.
.
.
+
x
n
+
.
.
.
=
1
1
−
x
(
−
1
<
x
<
1
)
\sum\limits_{n=0}^∞x^n=1+x+x²+x³+...+x^n+...=\dfrac{1}{1-x} \qquad (-1<x<1)
n=0∑∞xn=1+x+x2+x3+...+xn+...=1−x1(−1<x<1)
(2)变形:
∑
n
=
1
∞
x
n
=
x
+
x
2
+
x
3
+
.
.
.
+
x
n
+
.
.
.
=
x
1
−
x
(
−
1
<
x
<
1
)
\sum\limits_{n=1}^∞x^n=x+x²+x³+...+x^n+...=\dfrac{x}{1-x} \qquad (-1<x<1)
n=1∑∞xn=x+x2+x3+...+xn+...=1−xx(−1<x<1)
∑ n = 0 ∞ ( − 1 ) n x n = 1 − x + x 2 − x 3 + . . . + ( − 1 ) n x n + . . . = 1 1 + x ( − 1 < x < 1 ) \sum\limits_{n=0}^∞(-1)^nx^n=1-x+x^2-x^3+...+(-1)^nx^n+...=\dfrac{1}{1+x} \qquad (-1<x<1) n=0∑∞(−1)nxn=1−x+x2−x3+...+(−1)nxn+...=1+x1(−1<x<1)
逐项求导、逐项积分求和函数 S(x)
(1)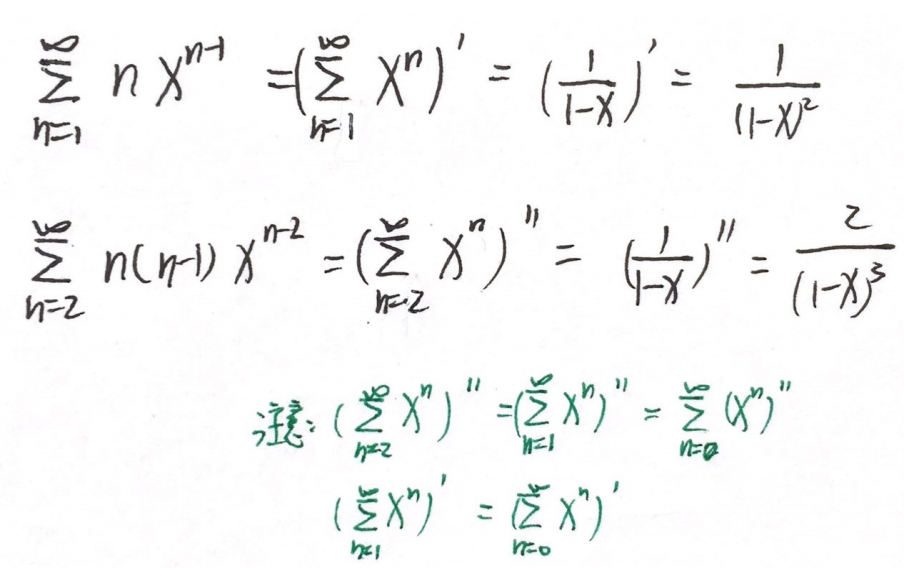
(2)①有分子就先积分消分子,凑标杆为函数,再求导。
②有分母就先求导消分母,凑标杆为函数,再积分。
一次求导(到凑标杆),对应一次积分。两次求导(到凑标杆),对应两次积分
一次积分(到凑标杆),对应一次求导。两次积分(到凑标杆)。对应两次求导
例题1:17年12. 积分消分子,凑标杆,再求导回来

分析:

答案: 1 ( 1 + x ) 2 \dfrac{1}{(1+x)²} (1+x)21
例题2:05年16. 求收敛区间、和函数
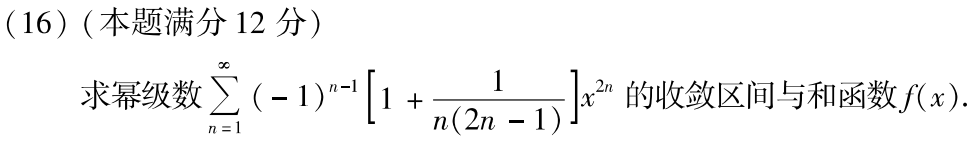
答案:

例题3:23李林四(一)14.
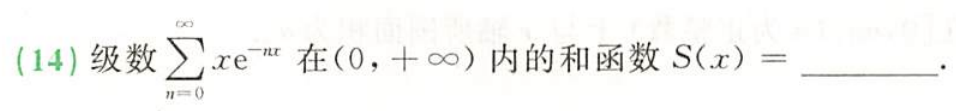
分析:
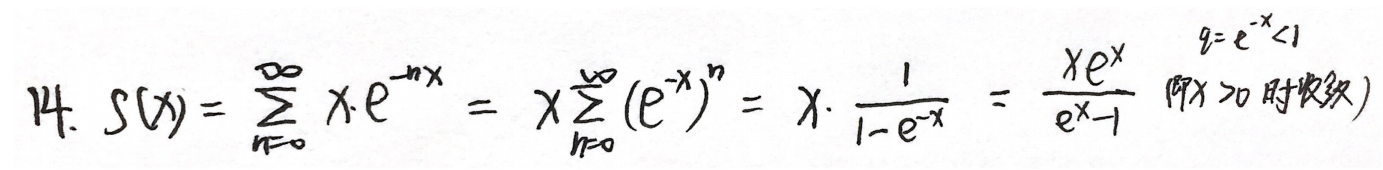
答案:
x
e
x
e
x
−
1
(
x
>
0
)
\dfrac{xe^x}{e^x-1}(x>0)
ex−1xex(x>0)
构造微分方程求和函数 S(X)
含有常数项递推式,求和函数,一般是需要对S(x)求导,找到一阶微分方程,用公式法求解y=S(x)
例题1:20年17.
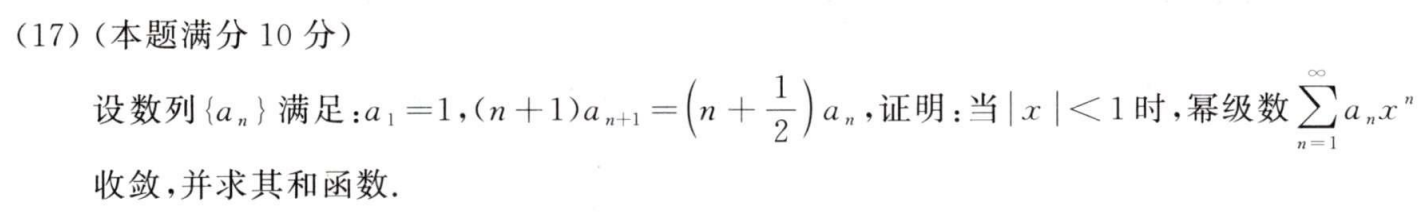
答案:

6.幂级数与常数项级数的相互转化
∑ n = 0 ∞ a n \sum\limits_{n=0}^∞a_n n=0∑∞an 是 x=1时的 ∑ n = 0 ∞ a n x n \sum\limits_{n=0}^∞a_nx^n n=0∑∞anxn
例题1:15年3. 幂级数与常数项级数的转化、阿贝尔定理推论2

分析:

答案:B
(二)三角级数
1.傅里叶级数
形如下式的级数叫做三角级数
a
0
2
+
∑
n
=
1
∞
(
a
n
cos
n
π
t
l
)
+
b
n
sin
n
π
t
l
)
\frac{a_0}{2}+\sum_{n=1}^∞(a_n\cos\frac{nπt}{l})+b_n\sin\frac{nπt}{l})
2a0+n=1∑∞(ancoslnπt)+bnsinlnπt)
令
π
t
l
=
x
\dfrac{πt}{l}=x
lπt=x,三角级数可变为
a
0
2
+
∑
n
=
1
∞
(
a
n
cos
n
x
)
+
b
n
sin
n
x
)
\frac{a_0}{2}+\sum_{n=1}^∞(a_n\cos nx)+b_n\sin nx)
2a0+n=1∑∞(ancosnx)+bnsinnx)
这就把以
2
l
2l
2l 为周期的三角级数转换成以
2
π
2π
2π 为周期的三角级数。
2.傅里叶系数、傅里叶级数
傅里叶系数:
{
a
n
=
1
π
∫
−
π
π
f
(
x
)
cos
n
x
d
x
(
n
=
0
,
1
,
2
,
3
,
.
.
.
)
b
n
=
1
π
∫
−
π
π
f
(
x
)
sin
n
x
d
x
(
n
=
1
,
2
,
3
,
.
.
.
)
\left\{\begin{aligned} a_n=\frac{1}{π}\int_{-π}^{π}f(x)\cos nx{\rm d}x \quad (n=0,1,2,3,...)\\ b_n=\frac{1}{π}\int_{-π}^{π}f(x)\sin nx{\rm d}x \qquad (n=1,2,3,...) \end{aligned}\right.
⎩
⎨
⎧an=π1∫−ππf(x)cosnxdx(n=0,1,2,3,...)bn=π1∫−ππf(x)sinnxdx(n=1,2,3,...)
傅里叶级数:
f
(
x
)
=
a
0
2
+
∑
n
=
1
∞
(
a
n
cos
n
x
+
b
n
sin
n
x
)
f
n
(
x
)
=
a
0
2
+
∑
k
=
1
n
(
a
k
cos
k
x
+
b
k
sin
k
x
)
f
1
(
x
)
=
a
0
2
+
a
1
cos
x
+
b
1
sin
x
f(x)=\frac{a_0}{2}+\sum_{n=1}^∞(a_n\cos nx+b_n\sin nx)\\[5mm] f_n(x)=\frac{a_0}{2}+\sum_{k=1}^n(a_k\cos kx+b_k\sin kx)\\[1mm] f_1(x)=\frac{a_0}{2}+a_1\cos x+b_1\sin x
f(x)=2a0+n=1∑∞(ancosnx+bnsinnx)fn(x)=2a0+k=1∑n(akcoskx+bksinkx)f1(x)=2a0+a1cosx+b1sinx
例题1:03年3.
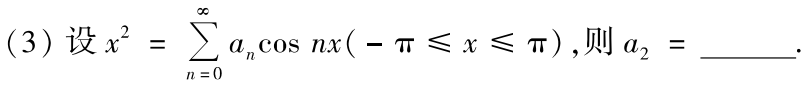
分析:这里建议使用表格法积分
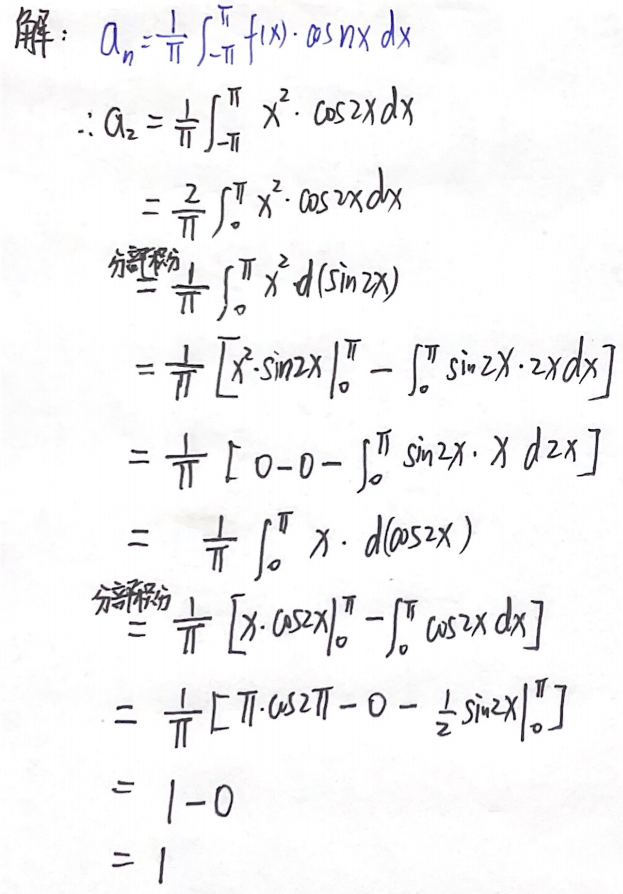
答案:1
例题2:14年4.
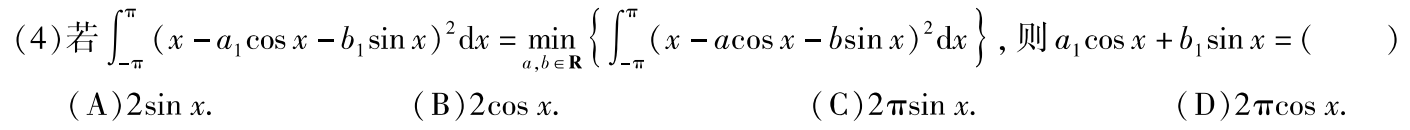
分析:①傅里叶级数 ②直接计算积分 ③代入选项求积分比最小

答案:A
3.正弦级数、余弦级数
已知傅里叶系数为:
{
a
n
=
1
π
∫
−
π
π
f
(
x
)
cos
n
x
d
x
(
n
=
0
,
1
,
2
,
3
,
.
.
.
)
b
n
=
1
π
∫
−
π
π
f
(
x
)
sin
n
x
d
x
(
n
=
1
,
2
,
3
,
.
.
.
)
\left\{\begin{aligned} a_n=\frac{1}{π}\int_{-π}^{π}f(x)\cos nx{\rm d}x \quad (n=0,1,2,3,...)\\ b_n=\frac{1}{π}\int_{-π}^{π}f(x)\sin nx{\rm d}x \qquad (n=1,2,3,...) \end{aligned}\right.
⎩
⎨
⎧an=π1∫−ππf(x)cosnxdx(n=0,1,2,3,...)bn=π1∫−ππf(x)sinnxdx(n=1,2,3,...)
①当
f
(
x
)
为奇函数
f(x)为奇函数
f(x)为奇函数时,
f
(
x
)
cos
n
x
f(x)\cos nx
f(x)cosnx是奇函数,
f
(
x
)
sin
n
x
f(x)\sin nx
f(x)sinnx是偶函数,故
{
a
n
=
0
(
n
=
0
,
1
,
2
,
3
,
.
.
.
)
b
n
=
2
π
∫
0
π
f
(
x
)
sin
n
x
d
x
(
n
=
1
,
2
,
3
,
.
.
.
)
\left\{\begin{aligned} a_n=0 \qquad \qquad \qquad \qquad (n=0,1,2,3,...)\\ b_n=\frac{2}{π}\int_0^{π}f(x)\sin nx{\rm d}x \quad (n=1,2,3,...) \end{aligned}\right.
⎩
⎨
⎧an=0(n=0,1,2,3,...)bn=π2∫0πf(x)sinnxdx(n=1,2,3,...)
②当
f
(
x
)
为偶函数
f(x)为偶函数
f(x)为偶函数时,
f
(
x
)
cos
n
x
f(x)\cos nx
f(x)cosnx是偶函数,
f
(
x
)
sin
n
x
f(x)\sin nx
f(x)sinnx是奇函数,故
{
a
n
=
2
π
∫
0
π
f
(
x
)
cos
n
x
d
x
(
n
=
0
,
1
,
2
,
3
,
.
.
.
)
b
n
=
0
(
n
=
1
,
2
,
3
,
.
.
.
)
\left\{\begin{aligned} a_n=\frac{2}{π}\int_0^{π}f(x)\cos nx{\rm d}x \qquad (n=0,1,2,3,...)\\ b_n =0 \qquad \qquad \qquad \qquad \quad \qquad (n=1,2,3,...) \end{aligned}\right.
⎩
⎨
⎧an=π2∫0πf(x)cosnxdx(n=0,1,2,3,...)bn=0(n=1,2,3,...)
即知
奇函数的傅里叶级数是只含有正弦项的正弦级数:
∑
n
=
1
∞
b
n
sin
n
x
\sum\limits_{n=1}^∞b_n\sin nx
n=1∑∞bnsinnx
偶函数的傅里叶级数是只含有余弦项的余弦级数: a 0 2 + ∑ n = 1 ∞ a n cos n x \dfrac{a_0}{2}+\sum\limits_{n=1}^∞a_n\cos nx 2a0+n=1∑∞ancosnx
4.奇延拓、偶延拓、周期延拓
奇延拓:把(0,π]上的奇函数延展为(-π,π]上的奇函数
偶延拓:把(0,π]上的偶函数延展为(-π,π]上的偶函数
周期延拓:从周期为(-π,π] 延展为周期为2π的周期函数
5.狄利克雷收敛定理
设f(x)是周期为2π的周期函数,若它满足:
(1)在一个周期内连续或只有有限个第一类间断点
(2)在一个周期内至多只有有限个极值点
那么f(x)的傅里叶级数收敛,并且
①当x是f(x)的连续点时,级数收敛于f(x) 和函数S(x)=f(x)
②当x是f(x)的间断点时,级数收敛于
1
2
[
f
(
x
−
)
+
f
(
x
+
)
]
\dfrac{1}{2}[f(x^-)+f(x^+)]
21[f(x−)+f(x+)] 和函数S(x)=间断点左右极限的平均值
S ( x ) = { f ( x ) , x 为连续点 f ( x − ) + f ( x + ) 2 , x 为间断点 S(x)=\left\{\begin{aligned} f(x) \quad \qquad ,& x为连续点 \\ \dfrac{f(x^-)+f(x^+)}{2},& x为间断点 \end{aligned}\right. S(x)=⎩ ⎨ ⎧f(x),2f(x−)+f(x+),x为连续点x为间断点
例题1:23李林四(四)14. 周期延拓

分析:
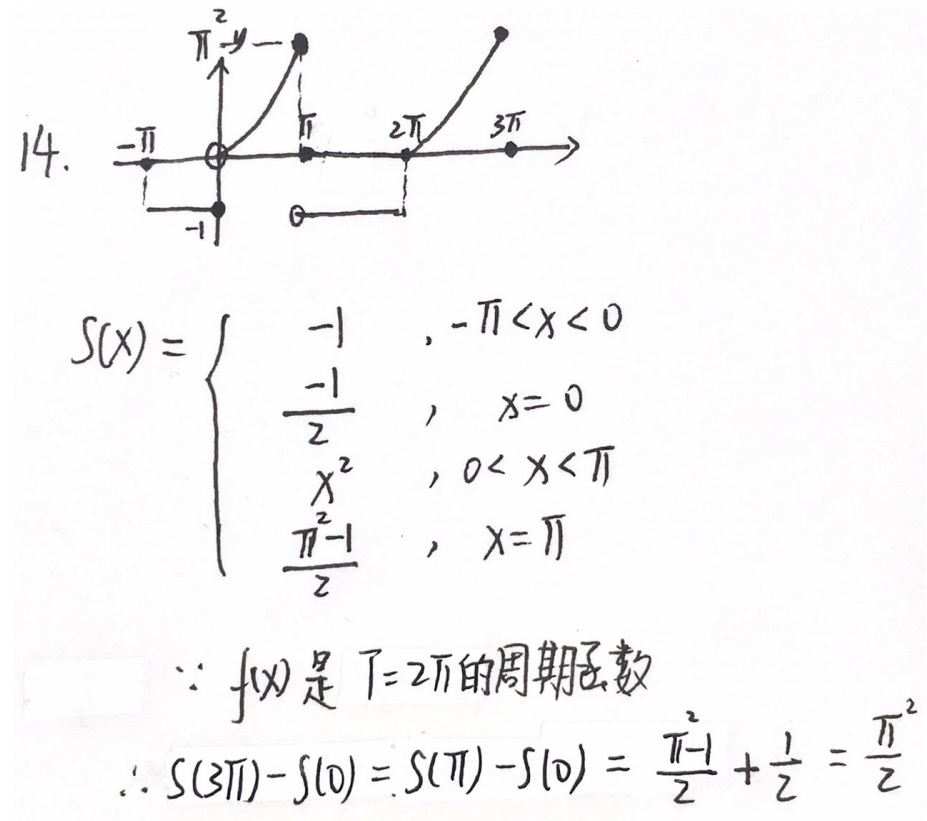
答案: π 2 2 \dfrac{π^2}{2} 2π2
例题2:13年3. 奇延拓、周期延拓
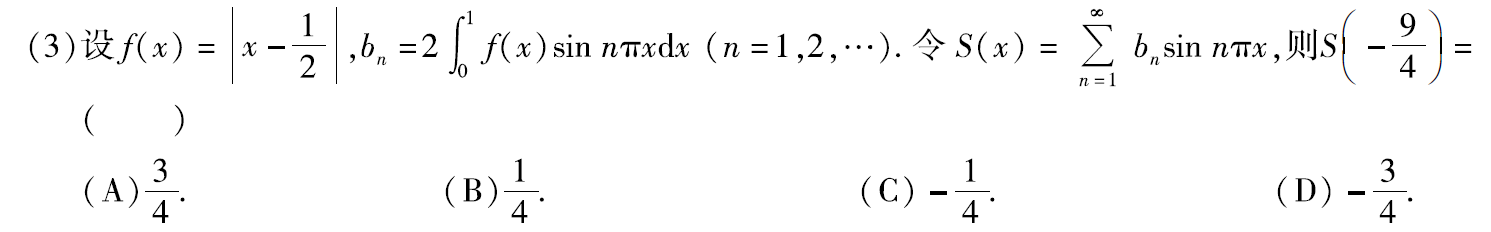
分析:
S(x)是奇函数的傅里叶级数的和函数
画出f(x)图像,把f(x)进行奇延拓、周期延拓,周期为2
S
(
−
9
4
)
=
S
(
−
9
4
+
2
)
=
S
(
−
1
4
)
=
−
S
(
1
4
)
=
连续点
狄利克雷收敛定理
−
f
(
1
4
)
=
−
∣
1
4
−
1
2
∣
=
−
1
4
S(-\frac{9}{4})=S(-\frac{9}{4}+2)=S(-\frac{1}{4})=-S(\frac{1}{4})\xlongequal[连续点]{狄利克雷收敛定理}-f(\frac{1}{4})=-|\frac{1}{4}-\frac{1}{2}|=-\frac{1}{4}
S(−49)=S(−49+2)=S(−41)=−S(41)狄利克雷收敛定理连续点−f(41)=−∣41−21∣=−41

答案:C
例题3:99年选择3 偶延拓、周期延拓
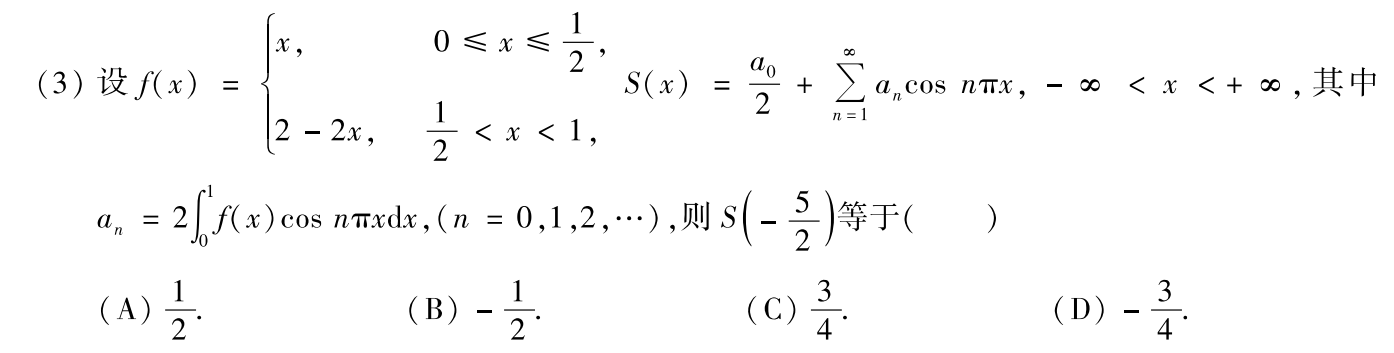
分析:
S(x)是偶函数的傅里叶级数的和函数
画出f(x)图像,把f(x)进行偶延拓、周期延拓,周期为2
S
(
−
5
2
)
=
S
(
−
5
2
+
2
)
=
S
(
−
1
2
)
=
S
(
1
2
)
=
间断点
狄利克雷收敛定理
1
2
+
1
2
=
3
4
S(-\frac{5}{2})=S(-\frac{5}{2}+2)=S(-\frac{1}{2})=S(\frac{1}{2})\xlongequal[间断点]{狄利克雷收敛定理}\dfrac{\frac{1}{2}+1}{2}=\dfrac{3}{4}
S(−25)=S(−25+2)=S(−21)=S(21)狄利克雷收敛定理间断点221+1=43
答案:C
相关文章
- 求用1g、2g、3g的砝码(每种砝码有无穷多个)称出10g的方案有几种
- 泛函编程(13)-无穷数据流-Infinite Stream
- java实现第六届蓝桥杯无穷分数
- java实现第六届蓝桥杯无穷分数
- java实现第六届蓝桥杯无穷分数
- java实现第六届蓝桥杯无穷分数
- java实现第六届蓝桥杯无穷分数
- 考研:研究生考试(十五天学完)之《高等数学上/下册》研究生学霸重点知识点总结之考试内容各科占比及常考知识重点梳理(函数极限连续、一元/多元函数微分学/积分学、常微分函数、向量代数与空间几何、无穷级数)
- 考研:研究生考试(十五天学完)之《高等数学上/下册》研究生学霸重点知识点总结之考试内容各科占比及常考知识重点梳理(函数极限连续、一元/多元函数微分学/积分学、常微分函数、向量代数与空间几何、无穷级数)
- 多种控制率算法的实现案例(LQR、H无穷和神经网络算法等)(Matlab代码实现)
- 利用numpy和matplotlib在坐标系中绘制方波的无穷级数表示
- 华为云MVP朱有鹏:做IoT开发乐趣无穷,年轻开发者更要厚积薄发
- 基于matlab的球形译码的理论原理和仿真结果,对比2norm球形译码,无穷范数球形译码,ML检测
- 【数字信号处理】相关函数 ( 相关函数性质 | 相关函数最大值 | 自相关函数最大值 | 互相关函数最大值 | 能量有限信号的相关函数在 m 趋近无穷时为 0 )
- SVM高斯核为何会将特征映射到无穷维?【转载】
- m通过matlab对比PID控制器,自适应PID控制器以及H无穷控制器的控制性能

