弹簧质点系统

Rope类构造函数的实现

对于一个有num_nodes个节点的绳子，共有num_nodes-1个弹簧部分。这些弹簧依次排列，从位置start排列到end。因此，第 i 个弹簧的起点为start + i * (end - start) / (num_nodes - 1)。一个弹簧的延伸长度和方向为(end - start) / (num_nodes - 1)，记为pos。之后，依次往Rope对象的成员masses和springs中添加节点和弹簧即可。

依次创建新的质点Mass对象，其位置就是上述的弹簧起点位置。弹簧两端为新创建的质点。

Rope::Rope(Vector2D start, Vector2D end, int num_nodes, float node_mass, float k, vector<int> pinned_nodes)
{
    // 一个弹簧的延伸长度和方向
    Vector2D pos = (end - start) / (num_nodes - 1);
    // 创建位于起点的第一个质点
    masses.push_back(new Mass(start, node_mass, false));
    // 依次创建之后的num_nodes个质点和弹簧，质点的pinned属性都为false
    for(int i=1; i<num_nodes; i++){
        // 第 i 个质点的位置为 start+i*pos
        masses.push_back(new Mass(start+i*pos, node_mass, false));
        // 弹簧两端为方才创建的相邻的两个质点
        springs.push_back(new Spring(masses[i-1], masses[i], k));        
    }
    // 将要求固定的质点的pinned属性记为true
    for (auto &i : pinned_nodes) {
        masses[i] -> pinned = true;
    }
}

编译运行程序，得到如下结果：

Euler模拟

2.1 代码编写

首先确定每个弹簧产生的力，施加在两端的质点上。由弹簧两端的质点的位置可以得到当前弹簧的长度和朝向。将两个质点的位置相减，得到向量direct。通过调用direct.norm()可以获取其长度。依据胡克定律，有：
$$F=k\Delta x$$
即弹力$F$为弹性系数$k$与弹簧形变长度$\Delta x$的乘积。弹性系数已经给出，将弹簧的自然长度减去上述的弹簧的当前长度即可算出弹力大小。弹力方向和弹簧方向一致。通过调用direct.unit()将该向量单位化即可得到方向。方向的正反需要考虑弹簧的哪一端，以及弹簧是压缩还是拉长。保证最后的预期符号正确即可。

方向和弹力大小相乘就能得到弹力，加到质点合力forces上即可。

for (auto &s : springs)
{
    Vector2D direct = s->m1->position - s->m2->position;
    // 弹力 = 弹性系数 * （弹簧自然长度 - 弹簧当前长度）
    double force = s->k * (s->rest_length - direct.norm());
    // 将弹力加到两端的质点的受力上，注意方向正负
    s->m1->forces += (force * direct.unit());
    s->m2->forces += (-force * direct.unit());
}

计算完弹力后，需要进行重力和阻尼的运算。依次遍历各个质点，进行计算。若质点固定则不需要计算。

重力已经给出，直接加到合力m->forces上即可。物体受到的阻力与速度成正比例，比例系数即为阻尼系数，是可以调整的参数。速度选用上一时刻物体的速度即可，方向与物体运动方向相反，即速度的反方向，合力减去阻尼系数乘以速度即可。

考虑了弹力、重力、阻力后，就能得到各个质点受到的合力，除以质量就得到了加速度。通过乘以给定的时间差delta_t，加上上一时刻的速度就得到了下一时刻的速度。通过速度就能得到下一时刻的物体位置。此处可以采用显式欧拉法，移动的距离为上一时刻的速度乘以时间差，或是半隐式欧拉法，位移为下一时刻的速度乘以时间差。

最后，将所有质点的合力清零，便于下一次计算。

for (auto &m : masses)
{	// 若质点固定则不考虑
    if (!m->pinned)
    {	// 加上重力
        m->forces += gravity;
        // 加上阻力
        double k_d = 0.01;
        m->forces -= (k_d*m->velocity);
        // 计算下一时刻的速度为位置
        // m->position = m->position + m->velocity * delta_t;	// 显式欧拉法
        m->velocity = m->velocity + m->forces / m -> mass * delta_t;
        m->position = m->position + m->velocity * delta_t;		// 半隐式欧拉法
    }
    // Reset all forces on each mass
    m->forces = Vector2D(0, 0);
}

2.2 调参与运行结果

将application.cpp中的质点数改为16：

ropeEuler = new Rope(Vector2D(0, 200), Vector2D(-400, 200), 16, config.mass,
                       config.ks, {0});

显式与半隐式欧拉法

将阻尼系数设置为0.001，步数为默认值64，比较显示和半隐式欧拉法。

显示欧拉法先更新位置再更新速度：

m->position = m->position + m->velocity * delta_t;	// 显式欧拉法
m->velocity = m->velocity + m->forces / m -> mass * delta_t;

半隐式欧拉法先更新速度再更新位置：

m->velocity = m->velocity + m->forces / m -> mass * delta_t;
m->position = m->position + m->velocity * delta_t;		// 半隐式欧拉法

使用半隐式欧拉法，能够成功地得出模拟结果，绳子正常摆动，过了一段时间趋于竖直的稳定状态：

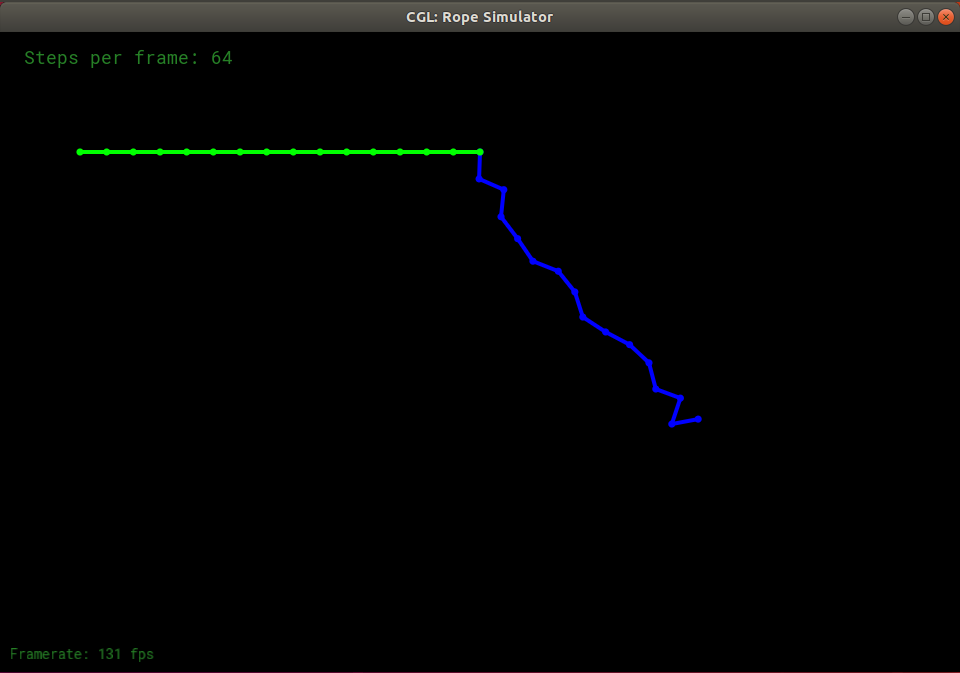
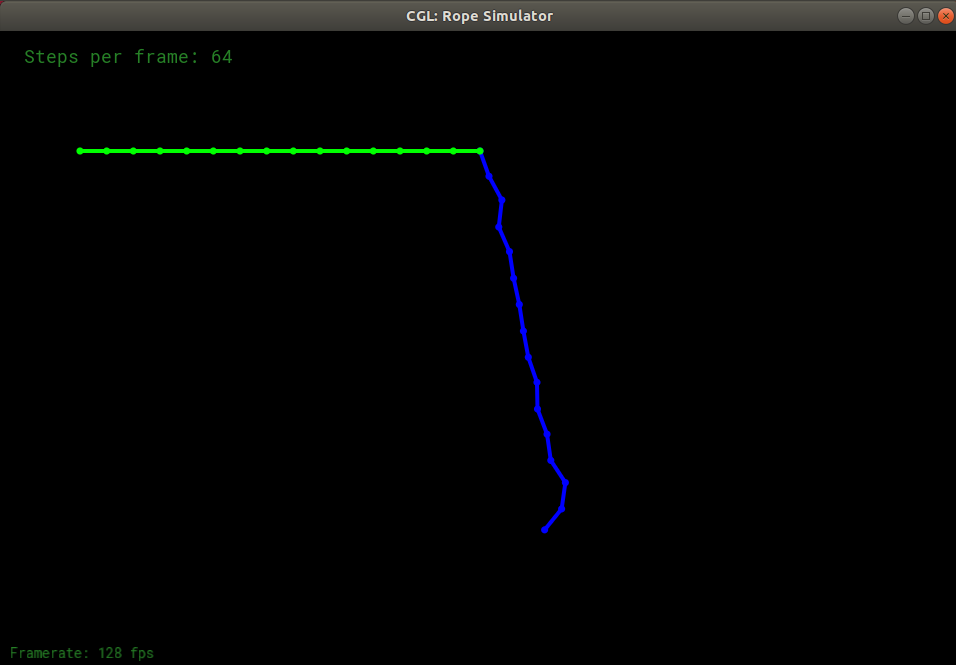
而在显示欧拉方法中，绳子鬼畜了一下，很快就消失了：

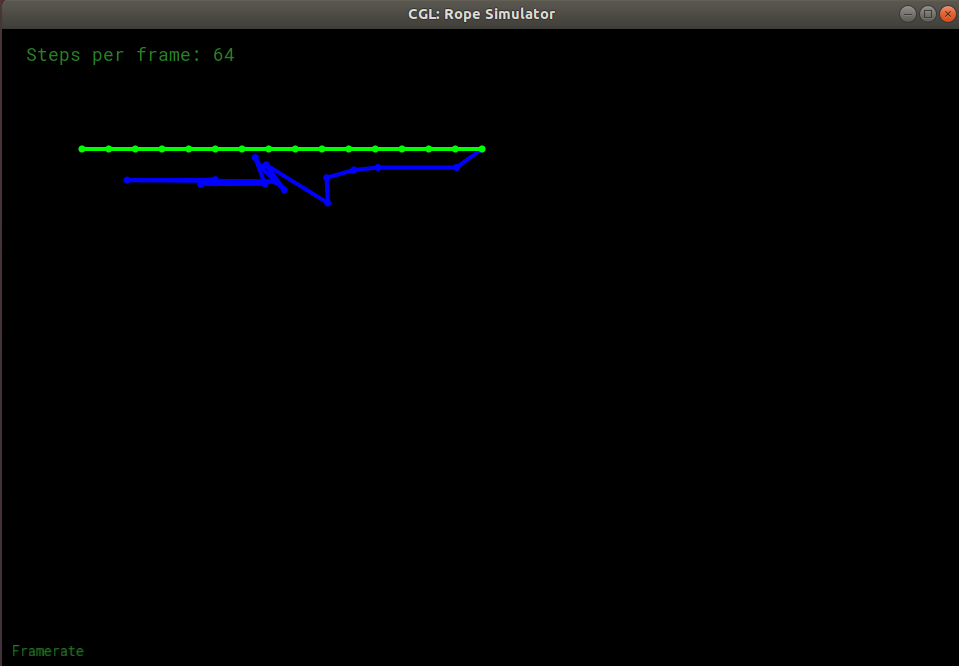
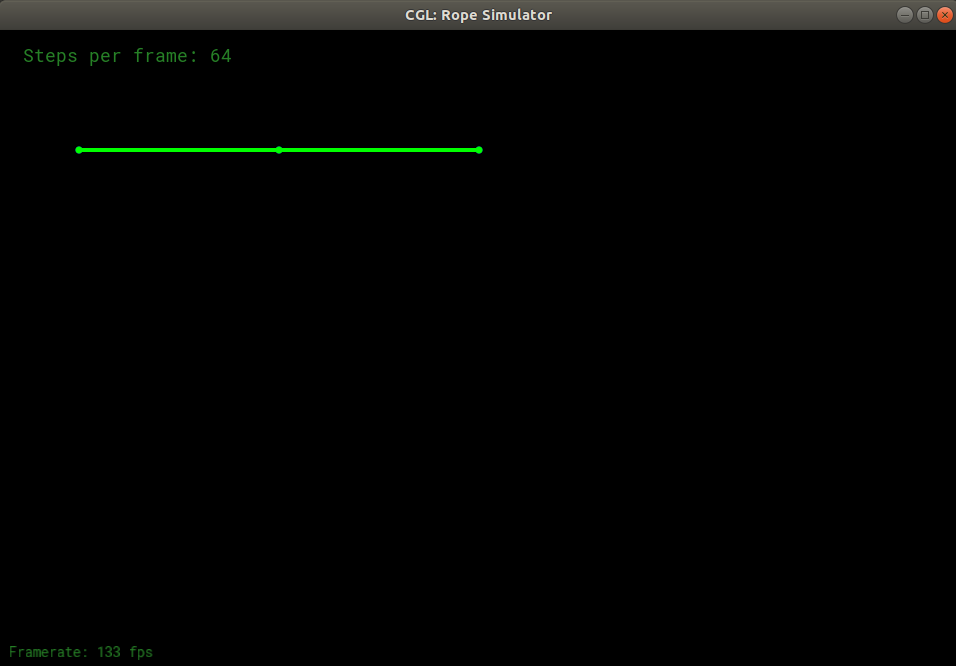
经过反复尝试，我发现当步数设置得很大时，显示欧拉法在早期能够普通地进行绳子的摆动，之后的震荡越来越不正常，直至绳子被拉的很长。将步长设置为1024时，其中的两张截图如下：

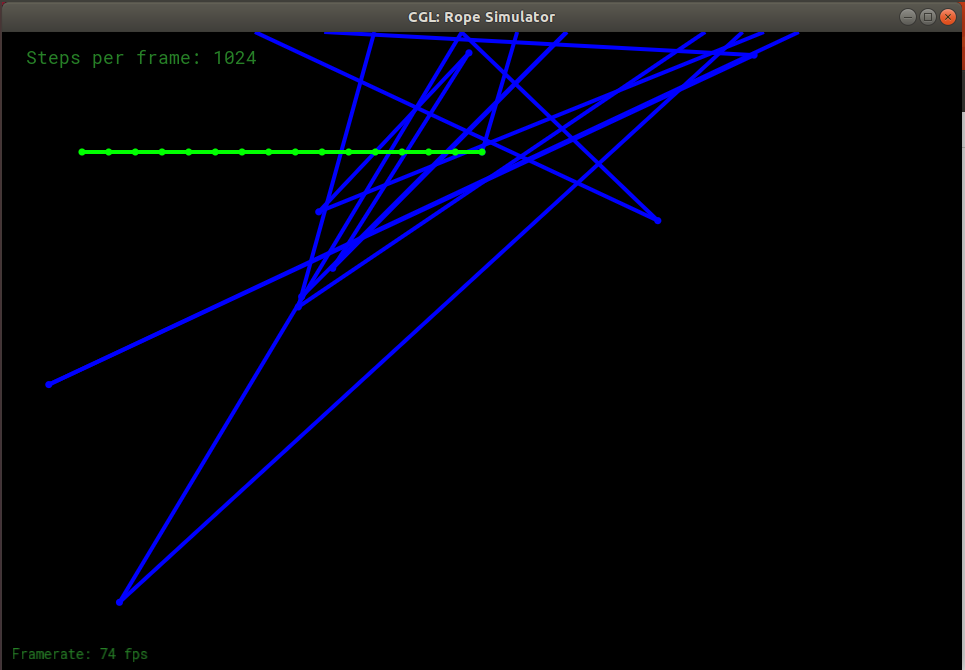
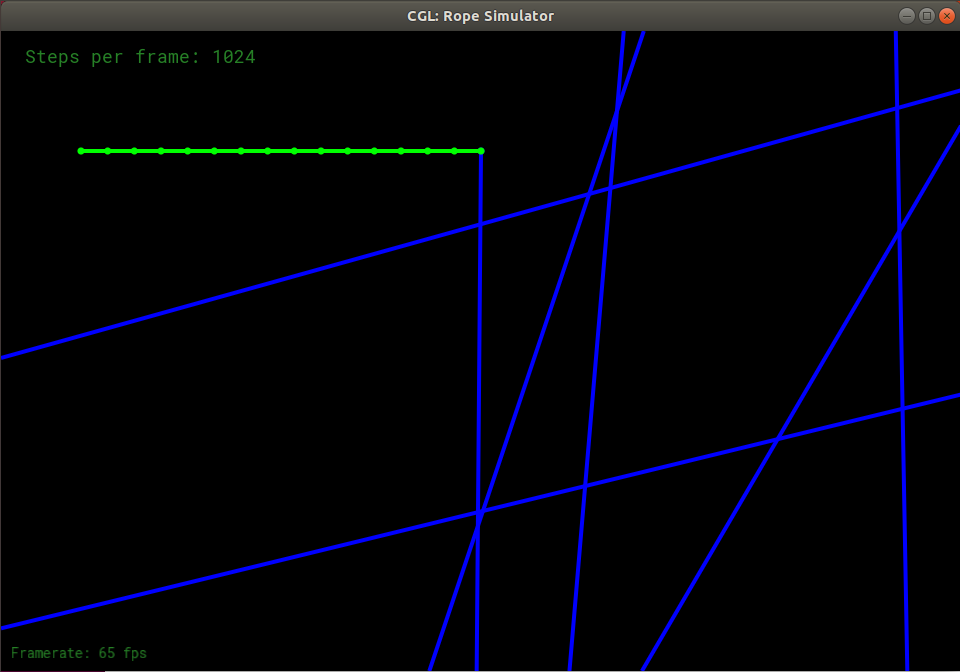
这是因为显示欧拉法不不稳定。考虑下面的一阶常微分方程：
$$\begin{gathered} \dot{x}(t)=-\lambda x(t) \\ x(0)=\hat{x} \end{gathered}$$
其中，$x(t)$为 $t$ 时刻的质点位置，$\dot{x}(t)$为此时的速度，位置的初始值为$x(0)=\hat{x}$，正数$\lambda$为参数。将上式代入显示欧拉法公式有：
$$x(t+1)=x(t)-\lambda x(t)\ast \Delta t$$
通过数学归纳法解得：
$$x(t+1)=(1-\lambda \Delta t{)}^{n+1}\hat{x}$$
这是个指数函数。当时间步长小于$\frac{2}{\lambda }$时，条件稳定，即不会发生指数爆炸。否则，系统不稳定，就会得到上述的结果，随着时间递进，参数数值变得很大，即发生了参数爆炸。在程序运行时，数值爆炸后位置参数变成了nan，不能读出确切的位置，因此打印不出绳子，看上去绳子消失了。

在我们的程序中，FPS是基本确定的，也就是说，每一帧的时间可以认为是定值。在步长较小时，每一步的时长越长，就越可能导致不稳定的结果。随着步长的逐渐增大，每一步的时间减少，则需要更多的时间系统的参数才会到达巨大的值，从而延长了数值爆炸的时间。这就是为什么步数为64时马上就会出现参数爆炸问题，而1024时会正常震荡一会儿才爆炸。理论上，只要步数够大，就能达到稳定。

步数调整

我在阻尼系数为0.001，步数为16、64、256、1024四种情况下对两种绳子进行了测试。

正如上面分析的一样，使用显示欧拉法的绳子不稳定，但随着步数的增大，绳子达到数值爆炸的时间明显增长了。而使用半隐式欧拉法的绳子在这几个绳子的参数下都能稳定，在反复摆动后停留在竖直状态。然而，半隐式方法并不是无条件稳定的。在步数降为9甚至更低时，半隐式方法的绳子也会产生参数爆炸的现象。

阻尼系数调整

设置步数为默认的64，依次将阻尼系数设置为0、0.001、0.01、0.1。考虑到显示欧拉法的绳子不稳定，下面只使用半隐式欧拉法的绳子。

在阻尼系数为 0 时，绳子不断抽动，停不下来。这是很好理解的。只考虑恒定重力和弹簧弹力的理想条件下，达到了物理的机械能守恒状态，动能、重力势能、弹性势能不断转换，导致系统不能稳定在某一恒定状态。

随着阻尼系数的增大，考虑了阻力的影响，会不断消磨机械能，导致最后整个系统稳定在绳子竖直垂下的状态。阻尼系数越大，则相同条件下的阻力越大，机械能消耗越多，因此到达最终稳定位置的时间就越快。在阻尼系数到0.1时，几乎是绳子首次下落到最低点就已经稳定。

Verlet模拟

3.1 代码编写

先在application.cpp中将绳子节点数改为16：

ropeVerlet = new Rope(Vector2D(0, 200), Vector2D(-400, 200), 16, config.mass,
                      config.ks, {0});

首先计算弹簧的形变长度，移动弹簧两端的质点，从而使得弹簧形变量为0。两个质点的位置相减即可得到表示弹簧的方向和长度的向量。将长度与自然长度相减得到形变长度diff_length，再将上述向量单位化得到弹簧方向。接着调整质点位置即可。需要注意的是，如果两个质点中有一个是固定的，则只能将另一个移动diff_length长度，否则两个质点都移动diff_length / 2的长度。移动方向由长度差的正负和计算的方向direct共同决定，两个质点的移动方向相反。

for (auto &s : springs)
{	// 计算弹簧形变的方向和长度
    Vector2D direct = s->m1->position - s->m2->position;
    double diff_length = s->rest_length - direct.norm();
    direct = direct.unit();
    // 若有一个质点固定，则移动另一个质点diff_length长度
    if(s->m1->pinned){
        s->m2->position = s->m2->position - diff_length * direct;
    }
    else if(s->m2->pinned){
        s->m1->position = s->m1->position + diff_length * direct;
    }
    // 若都不固定，则两个质点各移动diff_length/2的距离
    else{
        s->m1->position = s->m1->position + diff_length * direct / 2;
        s->m2->position = s->m2->position - diff_length * direct / 2;
    }
}

接着依据Verlet的公式，利用重力更新位置。如果质点不固定，则直接将公式：
$$x(t+1)=x(t)+(1-k_d)\ast (x(t)-x(t-1))+a\ast dt\ast dt$$
代入即可。其中，$k_d$为阻尼系数，$a$为重力加速度，可以用重力除以质点质量得到，$dt$为时间间隔。因为公式使用了当前位置和上一位置，每次更新位置时还需要记录上一次的位置，即更新m->last_position。

for (auto &m : masses)
{
    if (!m->pinned)
    {
        Vector2D temp_position = m->position;
        double k_d = 0.00005;
        m->position = m->position + (1-k_d) * (m->position - m->last_position) + gravity / m->mass * delta_t * delta_t;
        m->last_position = temp_position;
    }
}

3.2 调参与运行结果

为了方便展示，我暂时将之前的欧拉绳子更新位置的语句注释掉了。

在步数为默认值64、阻尼系数为0.00005时，程序正常运行。过程中截图如下：

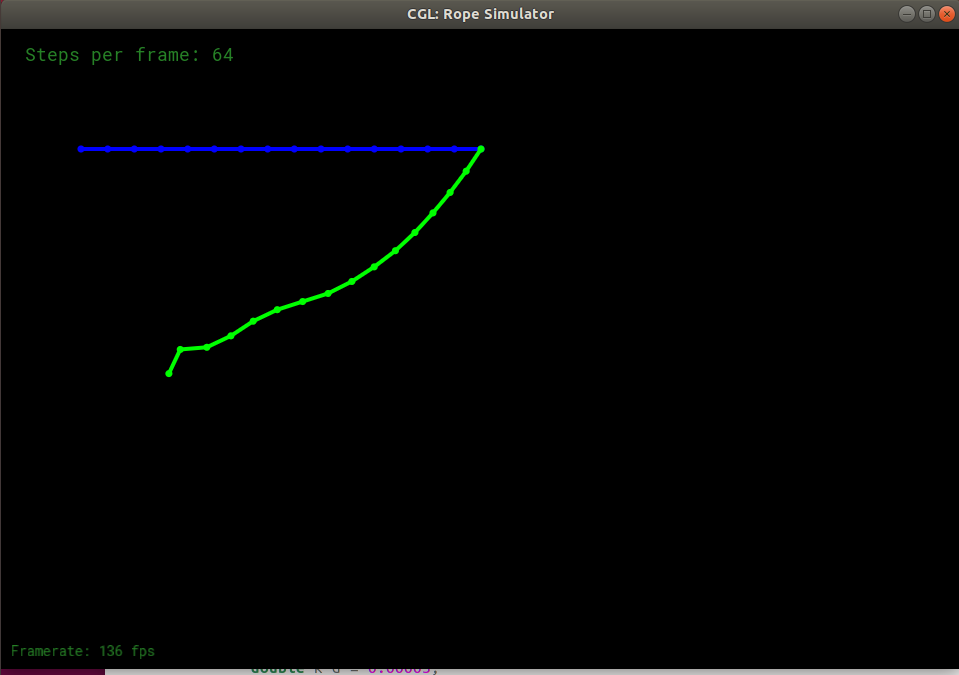
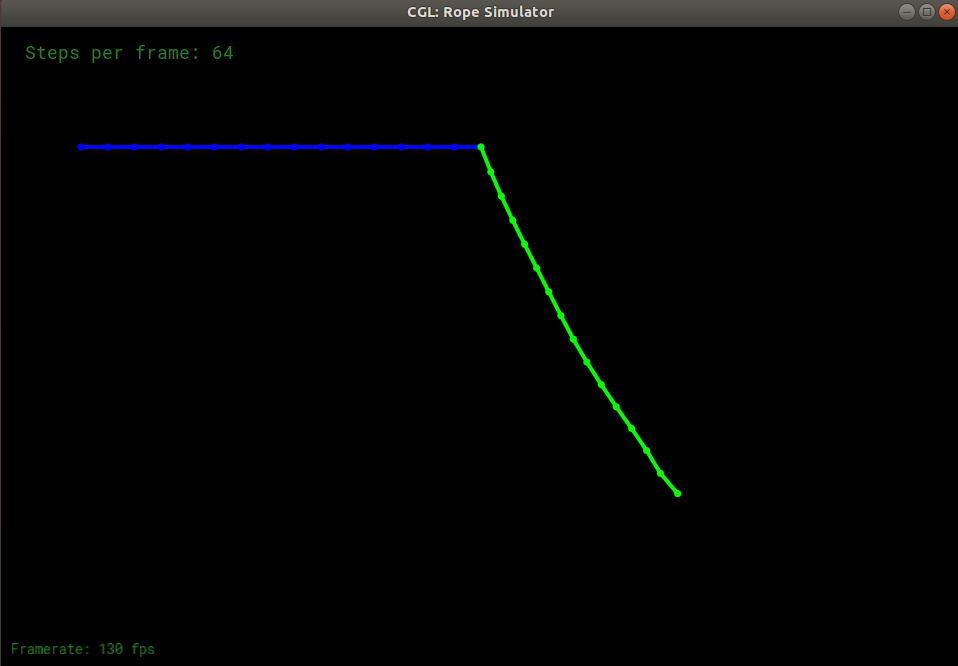
步数调整

我在阻尼系数为0.00005，步数为1、16、64、256、1024四种情况下对Verlet绳子进行了测试。

Verlet算法下的绳子是稳定的，在步数很低时也不会出现参数爆炸的情形。

随着步数的变大，绳子的运动变得越发平滑，同时到达稳定位置的速度越快。在步数较小，如16时，绳子会反复摆动很久才到达稳定位置，而在1024下却能很快就到达平衡位置。

在步数较低时，总体来说，绳子更像是模拟的那样，即质点与弹簧的集合。弹簧的伸长缩短的过程更加明显。随着步数的增加，绳子整体更像我们生活中所认知的绳子，长度几乎不变，像一般的绳子一样进行摆动。步数越多，则每一帧内由弹簧长度和重力影响的质点位移就越多次迭代，重力不变而弹簧形变不断被质点更新位移而归零，重力引发的形变又不足以使得绳子产生较大的弹力，达到稳定时往往会趋于原长；而步数少时，形变被质点移动消除后，重力又引发新的形变，弹簧的形变难以被完全制衡，随着帧数的增加，弹簧则会表现出更强的弹簧特性。

在步数为1（左边）和1024（右边）时的稳定状态的结果如下：

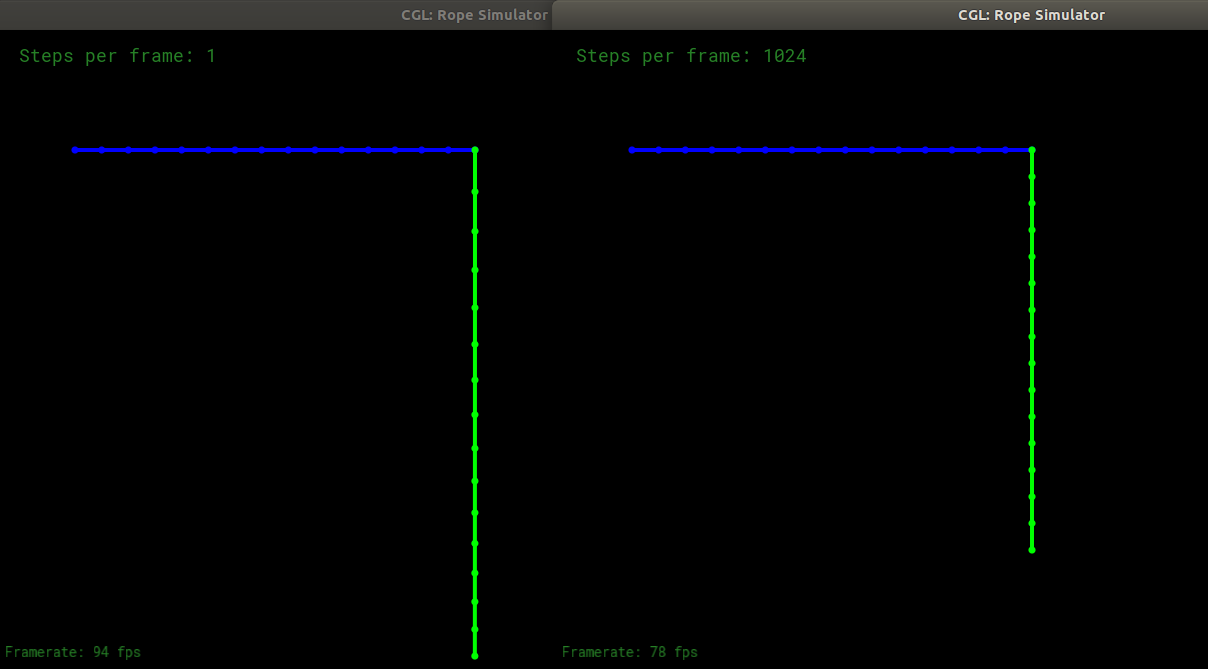
可以看出，左边的各段弹簧越靠上则下面吊的质点越多，因此就被拉得更长。直观来看，绳子整体更像是弹簧；下面的弹簧更短。而右图的各段弹簧基本都处于原长，整体更像是我们生活中所认知的绳子。

阻尼系数调整

我对阻尼系数依次为0、0.0000.5、0.0005、0.005进行了测试。

在阻尼为0时，系统仍能到达平衡位置。在步数较低时，进入平衡状态的速度更快。这说明verlet绳子系统下并不是机械能守恒的，即便没有阻力的影响，系统也不能持续运动。

而在阻尼系数增大后，绳子运动的速度放缓了。这在步数也较高的时候尤为明显，绳子就像是羽毛一样慢慢地飘了下来。因为绳子的速度的放缓，到达平衡时间可能反而变慢了，但到达平衡位置前的摆动次数变少了。这种改变在公式中是很直观的：阻尼系数影响了因重力产生的位移的大小。每一帧产生的位移减小了，看上去就是速度放缓了。

♻️ 资源

大小： 1.33MB
➡️ 资源下载：https://download.csdn.net/download/s1t16/87377754