RSA大作业 实验报告

程序使用说明

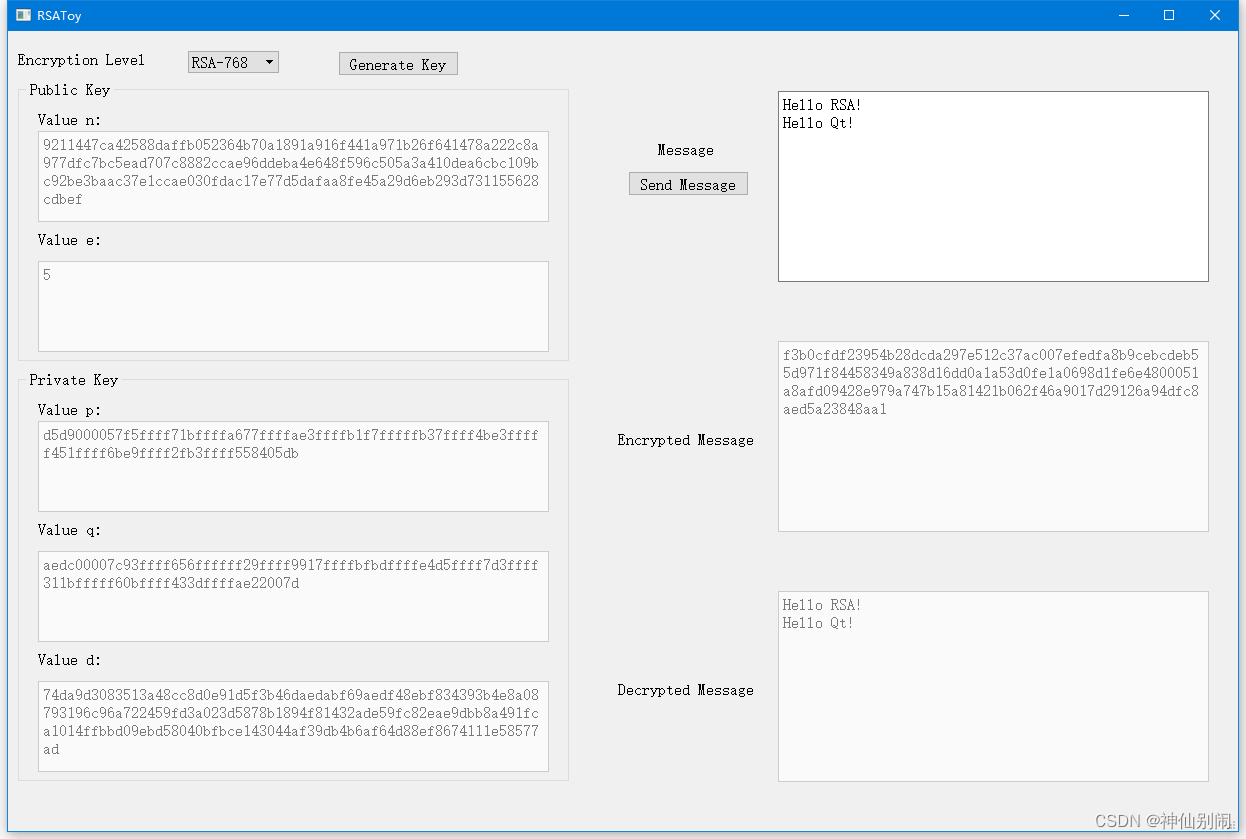
双击RSAToy.exe运行程序，界面主要分为两部分：

1. 左侧为RSA密钥生成部分，可以选择RSA-768，RSA-1024或者RSA-2048作为标准，并点击Generate Key按钮生成密钥。生成完成后，密钥中的$$p,q,n,e,d$$都会显示在文本框中。

2. 右侧为消息发送部分，用户可以在消息输入框输入要发送的消息(目前只支持ASCI编码)，并点击Send Message按钮即可发送消息。RSA算法会对消息先进行加密、再进行解密，并将加密和解密的结果都显示在对应的文本框中。

   (注：目前仅支持1080P分辨率，在较高分辨率如2k\3k\4k下界面可能会显示异常)

算法实现亮点

在本次大作业中，实现了如下基本算法：

1. 加、减、乘、除、移位、幂取模的高精度算法
2. 利用快速幂和牛顿迭代法加速取模运算
3. 中国剩余定理
4. Miller Rabin检测

在RSA密钥的生成过程中，大素数生成是时间瓶颈，因此在素数生成过程中，我使用了以下方法来进行优化或加速：

快速幂

在Miller Rabin算法中，需要多次进行幂取模运算$$a^d(\mathrm{mod}n)$$，其中$$a,d,n$$均为大整数，经过测试，这一步是Miller Rabin判据最耗时的步骤，因此，对这一步进行优化非常关键。对幂取模这一步运算做优化，最直观和简单的算法是快速幂算法。

在计算$$a^d(\mathrm{mod}n)$$时，如果$$d$$为偶数，那么可以计算$$(a^{\frac{d}{2}}{)}^2(\mathrm{mod}n)$$，如果$$d$$为奇数，那么可以计算$$(a^{\frac{d-1}{2}}{)}^{2}a(\mathrm{mod}n)$$，根据维基百科，快速幂的伪代码为：

function modular_pow(base, exponent, modulus) is
    if modulus = 1 then
        return 0
    Assert :: (modulus - 1) * (modulus - 1) does not overflow base
    result := 1
    base := base mod modulus
    while exponent > 0 do
        if (exponent mod 2 == 1) then
            result := (result * base) mod modulus
        exponent := exponent >> 1
        base := (base * base) mod modulus
    return result

不难发现，朴素的幂取模算法的时间复杂度为$$O(d)$$，而使用了快速幂之后，时间复杂度为$$O(log(d))$$.以$$RSA-768$$为例，$$d$$在二进制下是$$384$$位的整数，因此经过384次迭代即可得到结果，相比线性复杂度，节省了相当多的时间。

牛顿迭代法

使用快速幂算法之后，发现计算$$a^d(\mathrm{mod}n)$$的时间仍然很长，发现主要是计算$$a\mathrm{mod}n$$比较耗时，因为计算$$a\mathrm{mod}n$$需要使用高精度除法，当$$a$$远远大于$$n$$时，将会使用相当多次的减法，从而导致这一步非常耗时。

因此我使用了基于牛顿迭代法的求模算法，记$$n$$在二进制下有$$m$$位，该算法通过寻找$$n^{\prime }$$，使得$$(n{n}^{\prime })=1<<2m$$，这里$$<<$$是左移符号，这样$$a=a-((an{n}^{\prime })<<2m)(\mathrm{mod}n)$$.并且$$a\mathrm{mod}n$$与$$a-((an{n}^{\prime })<<2m)\mathrm{mod}n$$的值非常接近（事实上它们在大多数情况下是相等的），从而大大减少了减法的次数。

问题的关键在于：如何寻找$$n^{\prime }$$，这里我使用的是牛顿迭代法，定义函数$$f(x)=\frac{1<<2m}{x}-n$$,那么函数的零点即为$$n^{\prime }$$，从而可以使用牛顿迭代法求解。在实验中发现，通常经过10-20次迭代，就可以找到$$n^{\prime }$$.

同时，注意到，如果要计算多个$$a_0,a_1,...a_k$$对$$n$$的模，牛顿迭代法只需要计算一次即可，这又大大减少了取模的时间。

这一步优化是整个算法中最为关键的一步，如果不使用该方法，在几分钟的时间内甚至跑不完一次完整的Miller Rabin检测。

多线程

因为寻找素数的过程是可并行的，所以我利用了c++的多线程库，使用多线程来寻找素数。

我使用了多个线程同时判断整数的素性，并设置一个标志位，一旦某个线程找到一个素数，它将会修改此标志位，其余线程检查到标志位被修改后将会立刻退出。我使用了C++中的mutex来保护标志位以避免冲突。

其它小优化

1. 随机递增搜索。在寻找素数时，不必每次都随机生成一个数，然后判断它的素性。而是首先生成一个奇数$$n$$，如果$$n$$不是素数，就给$$n$$加$$2$$，重复此过程。在RSA-768下，平均需要380次即可找到一个素数。
2. 利用小素数优化。对一个未知素性的整数进行Miller Rabin检测之前，可以先尝试该整数能否整除小素数，以检测该整数的素性。因为Miller Rabin检测相对比较耗时，这样做可以尽可能减少Miller Rabin检测的次数。在实现中，我使用了$$10000$$以内的所有素数，在RSA-768下，平均找到每个素数仅需47次Miller Rabin检测。

实验结果

实验环境

操作系统: Windows 10

CPU: Intel® Core™ i7-8565U CPU @ 1.80GHz 1.99GHz

编程语言：C++

编译器：Microsoft Visual C++ Compiler16.4.29806.167

集成开发环境：Qt Creator(Qt 5.9.9 MSVC2015 64bit)

实验结果

在上述实验环境中，分别在RSA-768，RSA-1024和RSA-2048三种标准下生成100次公钥和密钥，并计算平均耗时，结果如下表所示：

附：一开始我是用的是MinGW编译器，不论怎么优化，生成RSA-768平均需要2s。走投无路之下，改用MSVC编译器，没想到速度快了4倍，真是蛋疼啊。。。。。。

♻️ 资源

大小： 19.7MB
➡️ 资源下载：https://download.csdn.net/download/s1t16/87354376