引言

上一节介绍了随机梯度变分推断(Stochastic Gradient Variational Inference,SGVI)。本节将介绍SGVI求解过程中遇到的问题，并针对为题介绍一种处理方法——重参数化技巧。

回顾：随机梯度变分推断

由于基于平均场假设的经典变分推断(Classical Variational Inference)的假设条件非常苛刻，基本无法在真实环境中使用。

因此，介绍了随机梯度变分推断，从$P(\mathcal{Z}\mid \mathcal{X})$整体角度进行求解。

SGVI的核心是将分布$\mathcal{Q}(\mathcal{Z})$视为概率模型，既然是概率模型，自然存在描述概率模型的模型参数。
这里定义 $\mathcal{Q}(\mathcal{Z})$的模型参数为$\varphi$，将求解$\mathcal{Q}(\mathcal{Z})$的梯度转化为求解模型参数$\varphi$的梯度。
实际上，$\mathcal{Q}(\mathcal{Z})$本身并不是‘隐变量的边缘概率分布’，而是条件概率分布$\mathcal{Q}(\mathcal{Z}\mid \mathcal{X})$。只是$\mathcal{X}$是观测数据，是已知量，因此省略。
$$\begin{gathered} \mathcal{Q}(\mathcal{Z})\to \mathcal{Q}(\mathcal{Z}\mid \varphi ) \\ \begin{array}{rl}\mathcal{L}[\mathcal{Q}(\mathcal{Z})]& ={\int }_{\mathcal{Z}\mid \varphi }\mathcal{Q}(\mathcal{Z}\mid \varphi )\cdot \log \left[\frac{P(\mathcal{X},\mathcal{Z})}{\mathcal{Q}(\mathcal{Z}\mid \varphi )}\right]d\mathcal{Z}\\ & =\mathcal{L}(\varphi )\end{array} \end{gathered}$$
随后$\mathcal{L}(\varphi )$对$\varphi$求解梯度，最终化简结果如下：
∇ ϕ L ( ϕ ) = E Q ( Z ∣ ϕ ) { ∇ ϕ log ⁡ Q ( Z ∣ ϕ ) ⋅ [ l o g P ( X , Z ) − log ⁡ Q ( Z ∣ ϕ ) ] } \nabla_{\phi} \mathcal L(\phi) = \mathbb E_{\mathcal Q(\mathcal Z \mid \phi)} \left\{ \nabla_{\phi} \log \mathcal Q(\mathcal Z \mid \phi) \cdot \left[log P(\mathcal X,\mathcal Z) - \log \mathcal Q(\mathcal Z \mid \phi)\right] \right\} ∇ϕ​L(ϕ)=EQ(Z∣ϕ)​{∇ϕ​logQ(Z∣ϕ)⋅[logP(X,Z)−logQ(Z∣ϕ)]}
至此，将梯度结果${\nabla }_{\varphi }\mathcal{L}(\varphi )$表示为期望形式，后续操作可以通过蒙特卡洛采样方法对期望结果进行估计。
假设从 概率模型$P(\mathcal{Z}\mid \varphi )$中采集了$N$个样本。即：
$$z^{(n)}\sim \mathcal{Q}(\mathcal{Z}\mid \varphi )(n=1,2,\cdots ,N)$$
上述期望使用蒙特卡洛采样方法近似表示为：
$${\nabla }_{\varphi }\mathcal{L}(\varphi )\approx \frac{1}{N}\sum _{n=1}^N\left\{{\nabla }_{\varphi }\log \mathcal{Q}(z^{(n)}\mid \varphi )\left[\log P(\mathcal{X},z^{(n)})-\log \mathcal{Q}(z^{(n)}\mid \varphi )\right]\right\}$$

随机梯度变分推断的问题

公式推导方式本身没有问题，问题在于采样过程中出现的高方差现象(High Variance)。该现象产生的具体原因如下：

• 观察基于蒙特卡洛方法的近似公式，大括号内主要包含两项，两项均包含$z^{(n)}$。观察第一项：
  $${\nabla }_{\varphi }\log \mathcal{Q}(z^{(n)}\mid \varphi )$$

• 注意，该项并不是求解$\log \mathcal{Q}(z^{(n)}\mid \varphi )$的结果，而是该结果的梯度。$\mathcal{Q}(z^{(n)}\mid \varphi )$是一个 描述概率的函数，因此它的值域是$(0,1)$。观察$\log \mathcal{Q}(z^{(n)}\mid \varphi )$在$(0,1)$范围内的结果以及梯度分别表示如下：
  
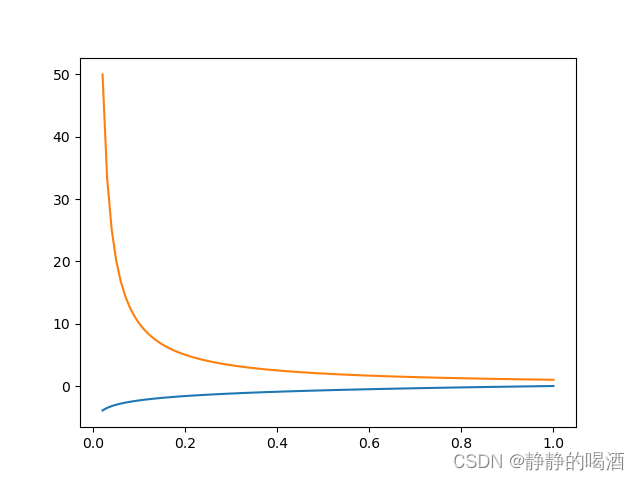
  其中橙色线表示梯度，蓝色线表示数值结果。由于 从$\mathcal{Q}(\mathcal{Z}\mid \varphi )$中采样$z$是纯随机采样，对应的结果$\mathcal{Q}(z\mid \varphi )$也必然是 $(0,1)$范围内的随机结果。那么对于极小的$\mathcal{Q}(z\mid \varphi )$结果对应的梯度反而是极高的数值。因此，采集出的样本中会存在少数数值极高的结果，从而对${\nabla }_{\varphi }\mathcal{L}(\varphi )$的近似计算产生更大的误差。

  本身通过蒙特卡洛方法求出的${\nabla }_{\varphi }\mathcal{L}(\varphi )$在梯度下降算法过程中就存在一定误差；如果${\nabla }_{\varphi }\mathcal{L}(\varphi )$也存在较大误差，这种误差叠加的结果自然使$\mathcal{Q}(\mathcal{Z}\mid \varphi )$的模型参数$\varphi$更加 难以保证其准确性。

至此，需要寻找方法，降低数据采样的高方差问题(Variance Reduction)。
本节将介绍通过重参数化技巧(Reparameterization Trick)来降低采样结果的高方差问题。

重参数化技巧

在对某概率分布$\mathcal{Q}(\mathcal{Z})$进行采样的过程中，如果直接从$\mathcal{Q}(\mathcal{Z})$中进行采样，可能出现高方差问题。

重参数化技巧的具体思想是：
已知条件：
随机变量$z$服从概率分布$\mathcal{Q}(z\mid \varphi )$。

• 随机变量$ϵ$服从某一分布$\mathcal{P}(ϵ)$，并且$ϵ$与$z$之间存在如下关系：
  $$z=\mathcal{G}(ϵ,\mathcal{X}\mid \varphi )$$
• 此时，可以通过对概率分布$\mathcal{P}(ϵ)$进行采样，通过与$ϵ$在$\mathcal{P}(ϵ)$中的期望间接求解$z$在概率分布$\mathcal{Q}(z\mid \varphi )$的期望结果。

示例：假设随机变量$z$服从均值为$\mu$，方差为${\sigma }^2$的高斯分布：
$$z\sim \mathcal{N}(\mu ,{\sigma }^2)$$
此时，想要求解上述概率分布下，关于$z$的函数$f(z)$的期望结果：
$${\mathbb{E}}_{\mathcal{P}(z)}[f(z)]$$
此时，存在一个随机变量$ϵ$，该变量服从于均值为0，方差为1的高斯分布：
$$ϵ\sim \mathcal{N}(0,1)$$
如何通过对$ϵ$进行采样从而对${\mathbb{E}}_{\mathcal{P}(z)}[f(z)]$进行求解？根据重参数化技巧，这里需要一个$z$和$ϵ$之间的关联关系：
$$z=\mathcal{G}(ϵ)=\mu +\sigma \times ϵ$$

${\mathbb{E}}_{\mathcal{P}(z)}[f(z)]$的求解过程如下：

• 将${\mathbb{E}}_{\mathcal{P}(z)}[f(z)]$展开为积分形式，并将$\mathcal{P}(z)$的 概率密度函数带入公式中：
  $$\begin{array}{rl}{\mathbb{E}}_{\mathcal{P}(z)}[f(z)]& ={\int }_z\mathcal{P}(z)f(z)dz\\ & ={\int }_z\left(\frac{1}{\sqrt{2\pi }\sigma }{e}^{-\frac{(z-\mu {)}^2}{2{\sigma }^2}}\right)\cdot f(z)dz\end{array}$$
• 将$z=\mathcal{G}(ϵ)$带入上式：
  $${\int }_{ϵ}\left(\frac{1}{\sqrt{2\pi }\sigma }{e}^{-\frac{(\mu +\sigma \cdot ϵ-\mu {)}^2}{2{\sigma }^2}}\right)f\left[\mathcal{G}(ϵ)\right]d[\mathcal{G}(ϵ)]$$
• 继续展开，得到如下结果：
  $$\begin{array}{rl}{\mathbb{E}}_{\mathcal{P}(z)}[f(z)]& ={\int }_{ϵ}\left(\frac{1}{\sqrt{2\pi }\sigma }{e}^{-\frac{(\mu +\sigma \cdot ϵ-\mu {)}^2}{2{\sigma }^2}}\right)f\left[\mathcal{G}(ϵ)\right]\cdot \sigma dϵ\\ & ={\int }_{ϵ}\frac{1}{\sqrt{2\pi }}{e}^{-\frac{{ϵ}^2}{2}}f[\mathcal{G}(ϵ)]dϵ\left(\frac{1}{\sqrt{2\pi }}{e}^{-\frac{{ϵ}^2}{2}}\to \mathcal{N}(0,1)\to \mathcal{P}(ϵ)\right)\\ & ={\int }_{ϵ}\mathcal{P}(ϵ)f[\mathcal{G}(ϵ)]dϵ\\ & ={\mathbb{E}}_{\mathcal{P}(ϵ)}[f[\mathcal{G}(ϵ)]]\end{array}$$
  至此，我们将 随机变量为$z$的期望转化为随机变量为$ϵ$的期望形式。

更泛化地说，只要$\mathcal{Q}(z)$和$\mathcal{P}(ϵ)$之间满足如下关系：
$$\mathcal{Q}(z)=\int \delta [z-\mathcal{G}(ϵ,\mathcal{X}\mid \varphi )]\mathcal{P}(ϵ)dϵ$$
都可以实现：
$${\mathbb{E}}_{\mathcal{Q}(z)}[f(z)]={\mathbb{E}}_{\mathcal{P}(ϵ)}[f[\mathcal{G}(ϵ,\mathcal{X}\mid \varphi )]]$$

基于重参数化技巧的求解过程

继续观察${\nabla }_{\varphi }\mathcal{L}(\varphi )$：
∇ ϕ L ( ϕ ) = E Q ( Z ∣ ϕ ) { ∇ ϕ log ⁡ Q ( Z ∣ ϕ ) ⋅ [ l o g P ( X , Z ) − log ⁡ Q ( Z ∣ ϕ ) ] } \nabla_{\phi} \mathcal L(\phi) = \mathbb E_{\mathcal Q(\mathcal Z \mid \phi)} \left\{ \nabla_{\phi} \log \mathcal Q(\mathcal Z \mid \phi) \cdot \left[log P(\mathcal X,\mathcal Z) - \log \mathcal Q(\mathcal Z \mid \phi)\right] \right\} ∇ϕ​L(ϕ)=EQ(Z∣ϕ)​{∇ϕ​logQ(Z∣ϕ)⋅[logP(X,Z)−logQ(Z∣ϕ)]}

• 假设存在$ϵ\sim \mathcal{P}(ϵ)$，并且$\mathcal{Z}$和$ϵ$满足：
  $$\mathcal{Z}=\mathcal{G}(ϵ,\mathcal{X}\mid \varphi )$$
  必然有：
  概率密度积分~
  $$\begin{array}{r}{\int }_{\mathcal{Z}}\mathcal{Q}(\mathcal{Z}\mid \varphi )d\mathcal{Z}={\int }_{ϵ}\mathcal{P}(ϵ)dϵ=1\end{array}$$
  从而有：
  $$|\mathcal{Q}(\mathcal{Z}\mid \varphi )d\mathcal{Z}|=|\mathcal{P}(ϵ)dϵ|$$
• 将上述变换直接带入${\nabla }_{\varphi }\mathcal{L}(\varphi )$中：
  $$\begin{array}{rl}{\nabla }_{\varphi }\mathcal{L}(\varphi )& ={\nabla }_{\varphi }{\int }_{\mathcal{Z}}\left[\log P(\mathcal{X},\mathcal{Z})-\log \mathcal{Q}(\mathcal{Z}\mid \varphi )\right]\cdot \mathcal{Q}(\mathcal{Z}\mid \varphi )d\mathcal{Z}\\ & ={\nabla }_{\varphi }{\int }_{\mathcal{Z}}\left[\log P(\mathcal{X},\mathcal{Z})-\log \mathcal{Q}(\mathcal{Z}\mid \varphi )\right]\cdot \mathcal{P}(ϵ)dϵ\end{array}$$
  使用牛顿-莱布尼兹公式将${\nabla }_{\varphi }$写入积分号中：
  $${\int }_{\mathcal{Z}}{\nabla }_{\varphi }\left[\log P(\mathcal{X},\mathcal{Z})-\log \mathcal{Q}(\mathcal{Z}\mid \varphi )\right]\cdot \mathcal{P}(ϵ)dϵ$$
  因为${\nabla }_{\varphi }$是对$\varphi$求解积分，因此和$\mathcal{P}(ϵ)$无关。进而化简得：
  $${\mathbb{E}}_{\mathcal{P}(ϵ)}[{\nabla }_{\varphi }(\log P(\mathcal{X},\mathcal{Z})-\log \mathcal{Q}(\mathcal{Z}\mid \varphi ))]$$
  为了将$\mathcal{Z}=\mathcal{G}(ϵ,\mathcal{X}\mid \varphi )$代入公式，通过链式求导法则，引入$\mathcal{Z}$，对${\nabla }_{\varphi }$进行重新表示：
  $${\mathbb{E}}_{\mathcal{P}(ϵ)}[{\nabla }_{\mathcal{Z}}(\log P(\mathcal{X},\mathcal{Z})-\log \mathcal{Q}(\mathcal{Z}\mid \varphi ))\cdot {\nabla }_{\varphi }\mathcal{Z}]$$
  最终将$\mathcal{Z}=\mathcal{G}(ϵ,\mathcal{X}\mid \varphi )$代入上式，则有：
  $$\begin{array}{r}{\mathbb{E}}_{\mathcal{P}(ϵ)}[{\nabla }_{\mathcal{Z}}(\log P(\mathcal{X},\mathcal{Z})-\log \mathcal{Q}(\mathcal{Z}\mid \varphi ))\cdot {\nabla }_{\varphi }\mathcal{G}(ϵ,\mathcal{X}\mid \varphi )]\end{array}$$
  至此，将最初始的基于$\mathcal{Q}(\mathcal{Z})$的期望转化为基于$\mathcal{P}(ϵ)$的期望。
  具体的执行流程如下：
• 从概率分布$\mathcal{P}(ϵ)$中获取$L$个样本：
  $${ϵ}^{(l)}\sim \mathcal{P}(ϵ)l=1,2,\cdots ,L$$
• 对期望结果进行处理：
  $$\begin{array}{rl}& {\mathbb{E}}_{\mathcal{P}(ϵ)}[{\nabla }_{\mathcal{Z}}(\log P(\mathcal{X},\mathcal{Z})-\log \mathcal{Q}(\mathcal{Z}\mid \varphi ))\cdot {\nabla }_{\varphi }\mathcal{G}(ϵ,\mathcal{X}\mid \varphi )]\\ & ={\mathbb{E}}_{\mathcal{P}(ϵ)}\left[\left(\frac{{\nabla }_{\mathcal{Z}}P(\mathcal{X},\mathcal{Z})}{P(\mathcal{X},\mathcal{Z})}-\frac{{\nabla }_{\mathcal{Z}}\mathcal{Q}(\mathcal{Z}\mid \varphi )}{Q(\mathcal{Z}\mid \varphi )}\right)\cdot {\nabla }_{\varphi }\mathcal{G}(ϵ,\mathcal{X}\mid \varphi )\right]\end{array}$$
• 将$\mathcal{Z}=\mathcal{G}(ϵ,\mathcal{X}\mid \varphi )$代入，此时整个期望中，就仅剩余$ϵ$一个变量。最后将${ϵ}^{(l)}(l=1,2,\cdots ,L)$代入， 使用蒙特卡洛方法求解均值近似期望结果 即可，最终近似求解${\nabla }_{\varphi }\mathcal{L}(\varphi )$。
  从而继续使用随机梯度变分推断，使用梯度上升法求解概率分布$\mathcal{Q}(\mathcal{Z}\mid \varphi )$的最优参数$\hat{\varphi }$：
  $${\varphi }^{(t+1)}\leftarrow {\varphi }^{(t)}+{\lambda }^{(t)}\cdot {\nabla }_{\varphi }\mathcal{L}(\varphi )$$

至此，变分推断部分的介绍结束。下一节将介绍马尔可夫链蒙特卡洛采样方法(Markov Chain Monte Carlo,MCMC)。

相关参考：
机器学习-变分推断5（随机梯度变分推断-SGVI-2）
机器学习：VAE重参数技巧一个细节理解