C#，骑士游历问题（Knight‘s Tour Problem）的恩斯多夫（Warnsdorff‘s Algorithm）算法与源代码

古往今来，对国际象棋及其战略游戏的迷恋鼓励了许多类型的复杂和分析性谜题。其中之一是《骑士之旅》，在过去的两个世纪里，它吸引了数学和游戏解决方案领域的一些最伟大的头脑。

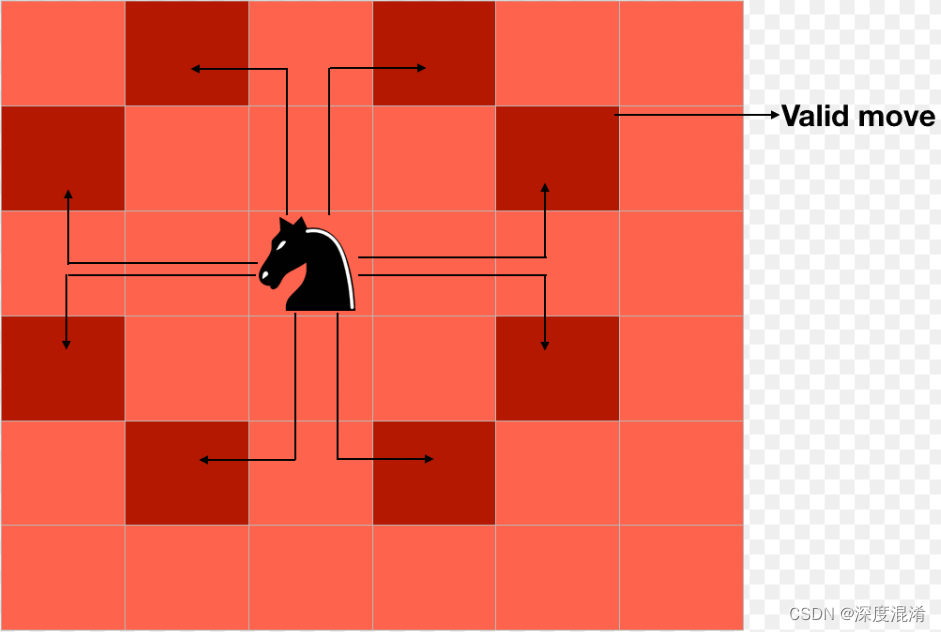
问题涉及在标准大小的棋盘上的任何位置放置一个棋子骑士，该棋盘由8X8配置的64个方块组成，然后将骑士从一个方块移动到另一个方块，直到所有64个方块都被访问一次且仅访问一次。国际象棋骑士的合法移动是在垂直或水平方向上两个方块，然后一个方块垂直于前一个方块（如图1所示）。

当你被介绍到这个谜题时，你的第一次尝试可能是把骑士放在棋盘上，然后在棋盘上任意移动。即使你知道如何在棋盘上移动骑士，你也会发现在两到三次尝试后，某些问题区域会出现。如果这些问题区域没有尽快消除，它们可能会发展成问题，最终会终止骑士的巡演。

此任意移动方法的示例如图2所示。骑士的行程由数字1到34表示，字母K表示骑士的当前位置。标有字母C的正方形表示可能的故障区域。故障区域是只有一个入口点和一个出口点的正方形。如图2箭头所示，如果骑士在任何相邻方块上着陆时未穿过该方块，则该方块将作为终止方块结束。在该示例中，正方形A和B是终止正方形。显然，如果在一次巡更中生成多个终止方块，则巡更无法完成。

这种任意的试错方法最终会产生问题的解决方案，但只有经过多次尝试和多次回溯之后。但由于无法保证行程将从任何给定点完成，数学家和谜题爱好者都试图找到不同的方法，无论骑士从何处出发，都可以找到解决方案。

早期方法

18世纪初，德莫伊夫、欧拉、勒让德、罗吉、范德蒙德和沃恩斯多夫等人为这个迷人的问题设计了一些非常艺术和实用的解决方案。要了解这些有趣的解决方案，请咨询W.W.R.Ball的数学再现和Eassays（Macmillan and Company，Ltd.，NY，1905）。

在这本书中讨论的许多方法中，作者找到了骑士之旅的奢侈解决方案。例如，一些人只对创建既可重复进入又在构图上对称的旅行感兴趣。重入式巡演是指骑士在最后一个方阵中只需一步就能回到最初的方阵。图3显示了此教程的一个示例，它在形式上是不对称的。

数学家们还对在完成的路线的编号平方之间找到某种算术关系感兴趣。一些人在寻找相邻正方形之间的奇偶关系，或是每行或每列中260个正方形的常数和。后一种方案产生了一个半幻方，其中对角线的总和不同；迄今为止，没有一种解决方案能够同时提供一个完美的魔方和一次完整的棋盘之旅。

J、 德国数学家C·沃恩斯多夫（C.Warnsdorff）几乎得出了所有可能的3100万个解。他的方法被称为沃恩斯多夫规则（Warnsdorff Rule）或双前瞻（double look ahead），指出骑士应该前进到下两步中可用方块数最小的方块。虽然1823年制定的这条规则从未被证明是准确的，但也从未发现过例外。Warnsdorff规则比任何其他规则都更适用于定位问题区域和为骑士提供提前消除问题的方法。

根据沃恩斯多夫规则，计算用于比较的数字可分为四个步骤。第一步是找到与骑士当前位置相邻的每个可用方块；在图4中，这些方块标有字母I、L和X。

第二步是从步骤1中标记的方块中计算可以访问的可用方块；所有与标记为I的正方形“相邻”的正方形都用字母O标记。因此，正方形的总数为七个，如图4中字母I上的下标所示。骑士目前占据的方格不计算在内。

第三步是计算从下标中指出的O平方可以达到的平方。

第四步是将步骤2和3中计算的所有数字相加；因此，为I平方计算的数字将是7+8+6+4+3+3+4+6，总共41个。L平方的数字为5+8+8+6+3+4或34。在为剩余的X标记方块计算完每个数字后，骑士移动到具有最小值的方块。通过这种方式，Warnsdorff能够提前看到可能的故障区域。

随着计算机的发明，一种全新的人群对骑士之旅产生了兴趣，这一问题可以通过计算机来解决。在过去的几年中，出现了新的尝试和修改的尝试，如巴耶拉夫·乔希教授对沃恩斯多夫规则的修改（创造性计算，1980年8月）。这些算法成功地完成了奈特的智能，但它们忽视了计算机半模拟人脑的能力。

计算机程序员过去的尝试对骑士的行动施加了许多限制；由于棋盘上只有64个可能的起始方块，每个算法只能产生64个不同的巡更。然而，如果比较不同算法生成的路径，yu会发现它们完全不同。

通过在算法中加入许多限制，程序员消除了计算机选择骑士下一步行动的能力。在骑士离开初始位置之前确定其路径的程序的一个例子是Joshi对Warnsdorff规则的修改。在他的算法中，Joshi认为最好告诉计算机将骑士移动到哪里，而不是让计算机选择将骑士移动到一个不完整的旅行中。然而，沃恩斯多夫法则确实允许算法选择骑士的下一步行动——如果计算出的最小数字之间存在平局。虽然从未证明这种随机选择会危及解决方案，但Joshi认为最好将其排除，从而将路由数量限制在64条。

新方法

即使程序中安装了任意选择，它仍然不会考虑所有可能的旅行。原因有两个：第一，提前检查两个动作有限制，第二，与第二级相邻方块相关的数字从一开始就固定。然而，这里介绍的方法只做一个限制，然后允许计算机在两个动作之间做出最终决定。计算机可以使用多种方法在移动之间进行任意选择。最常用的方法，也是我在程序中加入的方法，是随机数生成器。虽然这种方法本身永远无法模拟人脑的犹豫不决，但如果生成器在选择数字时确实是随机的，它就可以接近。

我开发的生成这个谜题的许多解决方案的算法，使用了Warnsdorff规则的一部分以及任意移动方法。我决定向前看，就像沃恩斯多夫（Warnsdorff）的规则一样，很重要，但不像乔希（Joshi）所做的那样重要。

通过向前看，Joshi保证了成功，但同时大大减少了做出武断决定的机会。因此，我决定只查看骑士当前位置附近的方块。算法从中选择相邻方块数最少的一个。这不仅确保了问题区域的消除，而且还增加了计算机必须做出决策的可能性，从而产生了一种高效的算法，可以为骑士之旅生成几乎无限数量的解决方案。

在介绍我的算法之前，我必须首先定义和解释确保正确结果所需的四个术语。首先，棋盘（CB）是一组8x8的正方形，每个正方形从左到右标记，从左上角的数字1开始（见图5）。

其次，表示新定义CB的平方的集合是：设S=（1,2,3，…64）。给定集合S，我可以定义S上的二元关系R，使得（a，b）在R中，当且仅当存在从a到b的合法移动。例如，对（1,11）在R中，而对（1,5）不在R中。由于对（11,1）也在R中，二元关系R被定义为S上的对称关系。这种对称关系允许更简单地确定骑士的下一步移动。图6所示的表格形式是算法计算的基础。

第三，CB上每个方块的退出值（EV）是在巡演过程中，在给定情况下从该方块合法移动的总数。该EV是通过扫描与表格形式的序列相关联的列，并计算每个发现的X来生成的，如图6所示。EV决定骑士在巡演中的下一步行动。

选择正确正方形的过程如下：1。）通过向下扫描相应的列，找到一个或多个EV最小的正方形，找到所有合法的正方形。2）如果存在多个小型电动汽车，请任意选择。应注意，在步骤1中选择最小EV的原因与Warnsdorff规则中所述的相同。第2步中的任意选择是我的算法产生不同行程的原因。

综上所述，算法如下：

步骤1：创建一个64 x 64矩阵，并通过在图6中表格形式中出现x的地方放置1，在其余正方形中放置0来初始化它。创建数组EV以存储上述64个值，并使用图6所示的值对其进行初始化。创建arry CB来存储骑士的移动，并创建变量KMC来跟踪骑士的移动。将KMC初始化为1。

步骤2：将对应于骑士当前位置（KMC）的矩阵行归零，并从相应列中找到1的每个EV中减去1。进行此减法的原因是为了避免在每次移动后在每列中计算1。

步骤3：检查骑士当前位置（KMC）所指的列，并找到EV最小的可用正方形。如果存在多个正方形，请使用随机数生成器确定下一步。

步骤4：将KMC增加1，并用新值标记CB数组中的正确位置。

步骤5：重复步骤2到4，直到KMC等于64（已找到完整的巡更），或者不再有可能移动到的方块。

步骤6：打印出CB数组，该数组现在包含骑士通过棋盘的当前路径。

我使用过时的Fortran IV版本在一台旧的IBM 1130计算机上测试了我的算法。我使用数字生成器在3秒钟的CPU时间内生成了20条不同的路线，而Joshi教授在APL的Itel as/6计算机上的时间为4.946秒。

然后，我在9.6秒内从同一起始广场生成了64条不同的路线。这与Joshi教授从不同出发点出发的64条行程的6秒时间相比。我的算法可能生成和测试的不同旅行次数取决于系统的随机数生成器。计算机内存应能够存储生成的每个新回路的计算结果，以便与之前由算法创建的其他回路进行比较。

源程序（POWER  BY  315SOFT.COM）

using System;
using System.Collections;
using System.Collections.Generic;

namespace Legalsoft.Truffer.Algorithm
{
	class Cell
	{
		public int X { get; set; } = 0;
		public int Y { get; set; } = 0;

		public Cell(int x, int y)
		{
			this.X = x;
			this.Y = y;
		}
	}

	public static partial class Algorithm_Gallery
	{
		private static Random rand { get; set; } = new Random((int)DateTime.Now.Ticks);

		public static int[] Move_Pattern_X = { 1, 1, 2, 2, -1, -1, -2, -2 };
		public static int[] Move_Pattern_Y = { 2, -2, 1, -1, 2, -2, 1, -1 };

		private static bool Limits(int N, int x, int y)
		{
			return ((x >= 0 && y >= 0) && (x < N && y < N));
		}

		private static bool IsEmpty(int N, int[] a, int x, int y)
		{
			return (Limits(N, x, y)) && (a[y * N + x] < 0);
		}

		private static int Get_Degree(int N, int[] a, int x, int y)
		{
			int count = 0;
			for (int i = 0; i < N; ++i)
			{
				if (IsEmpty(N, a, (x + Move_Pattern_X[i]), (y + Move_Pattern_Y[i])))
				{
					count++;
				}
			}
			return count;
		}

		private static Cell Next_Move(int N,ref int[] a, Cell cell)
		{
			int min_deg_idx = -1;
			int min_deg = (N + 1);

			int nx;
			int ny;
			int start = rand.Next() % N;
			for (int count = 0; count < N; ++count)
			{
				int i = (start + count) % N;
				nx = cell.X + Move_Pattern_X[i];
				ny = cell.Y + Move_Pattern_Y[i];
				int c = Get_Degree(N, a, nx, ny);
				if ((IsEmpty(N, a, nx, ny)) && (c) < min_deg)
				{
					min_deg_idx = i;
					min_deg = c;
				}
			}

			if (min_deg_idx == -1)
			{
				return null;
			}
			nx = cell.X + Move_Pattern_X[min_deg_idx];
			ny = cell.Y + Move_Pattern_Y[min_deg_idx];

			a[ny * N + nx] = a[(cell.Y) * N + (cell.X)] + 1;

			cell.X = nx;
			cell.Y = ny;

			return cell;
		}

		private static bool Neighbour(int N, int x, int y, int xx, int yy)
		{
			for (int i = 0; i < N; ++i)
			{
				if (((x + Move_Pattern_X[i]) == xx) && ((y + Move_Pattern_Y[i]) == yy))
				{
					return true;
				}
			}
			return false;
		}

		public static bool Find_Closed_Tour(int N, out int[] a)
		{
			a = new int[N * N];
			for (int i = 0; i < N * N; ++i)
			{
				a[i] = -1;
			}
			int sx = 3;
			int sy = 2;

			Cell cell = new Cell(sx, sy);

			a[cell.Y * N + cell.X] = 1;

			Cell ret = null;
			for (int i = 0; i < N * N - 1; ++i)
			{
				ret = Next_Move(N,ref a, cell);
				if (ret == null)
				{
					return false;
				}
			}

			if (!Neighbour(N, ret.X, ret.Y, sx, sy))
			{
				return false;
			}
			//print(a);
			return true;
		}
	}
}