提供了编程的基础技术教程

zl程序教程

您现在的位置是：首页 >  其它

当前栏目

复分析－欧拉公式的几何解读

解读 公式 几何 欧拉
2023-09-11 14:15:47 时间

常用的复数表达方式有很多种，比如最常见的一种

a+bi

还有一种类似于极坐标的表达方式

r\angle \theta

但是还有一种工程中应用最广发，最漂亮，奇迹般的表达方式，它就是大名鼎鼎的欧拉公式：

e^{i\theta}=cos(\theta)+i sin(\theta)

这个公式是欧拉再1740年左右发现的，那个时候乾隆才当了４年皇帝．

下面用运动的方式来图形化演示欧拉公式到底说了什么.

回忆一下一个基本的事实，e^x是它自身的导数，也就是

\frac{d}{dx}e^x=e^x

虽然是推导出来的，但是在微积分中，这是一个可以拿来作为定义的事实，也就是说，如果有人说一个函数满足

\frac{d}{dx}f(x)=f(x)

并且

f(0)=1

那么可以肯定的得到结论：

f(x)=e^x

类似的，如果k是一个实常数，则f(x)=e^{kx}和下面的条件等价

\frac{d}{dx}f(x)=kf(x)

并且

f(0)=1

为了把通常的指数函数e^x从x的实数域推广到虚数值，我们可以抓住这一点不放，坚定认定，当k=i时，此式为真，即:

\frac{d}{dx}e^{i\cdot t}=i\cdot e^t

实函数的导数理解为斜率，但是怎样理解虚函数的求导呢？

还记得在高等数学中，老师介绍微积分的时候，是通过速度，位移引入的，速度和位移同样都是矢量，可以用复数表示．

v(t)=\frac{d}{dt}f(t)=\lim_{\Delta s \to0 }\frac{f(t+\Delta s)-f(t)}{\Delta s}=\lim_{\Delta s \to0 }\frac{M}{\Delta s}

M是位移．

所以，无论是实数域还是复数域，给定了一个自变量的复函数，总可以把f(t)看成是运动过程中动点的位置，运用求导的方法，得到它的矢量速度．

把这个想法应用到

f(t)=e^{it}

上面，

v(t)=\frac{d}{dt}f(t)=ie^{it}=if(t)

上面的式子得到一个结论，就是速度始终和位置大小相同，但是垂直于当前的位置．

我们知道初始位置的值是

f(0)=e^0=1

所以运动过程的初始速度是i,也就是垂直向上运动，一段时间后，将运动到新的位置，而新位置的速度与新位置的向量仍然成直角，按照此种方法构造的运动，很明显，将会是如下方式的圆运动：　

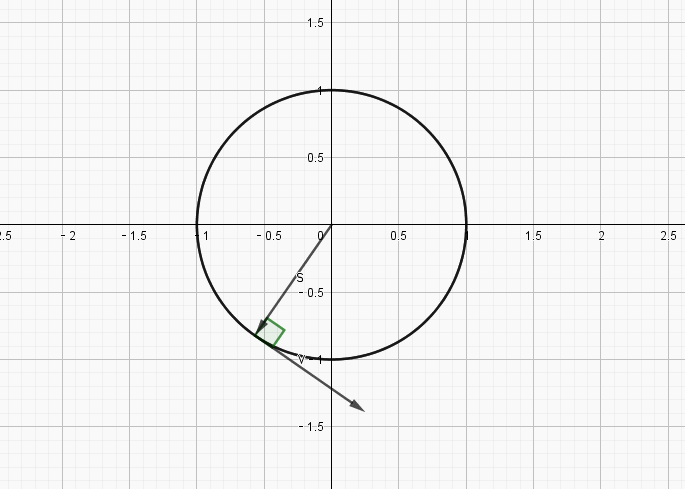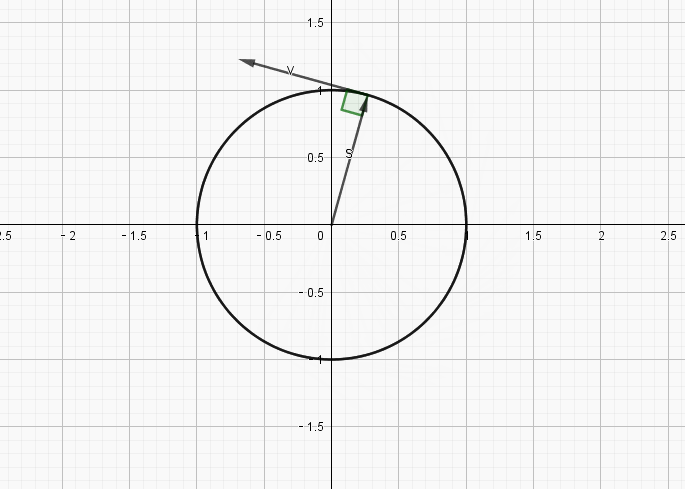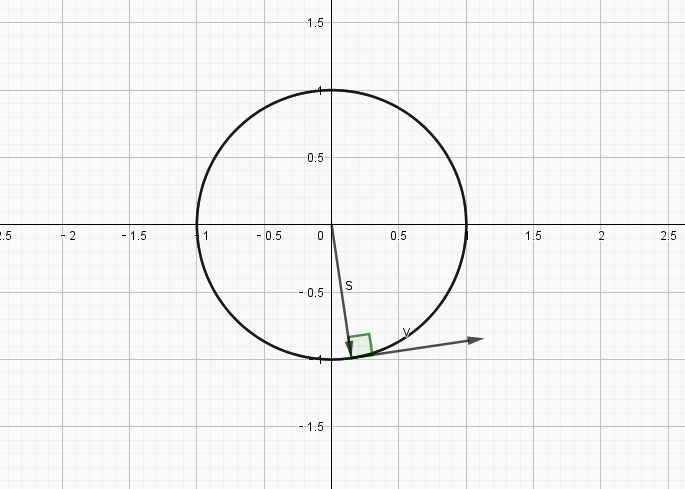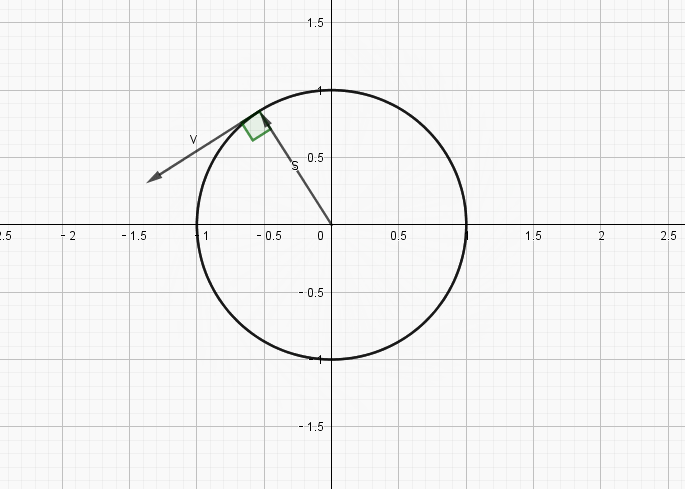
接下来看一下，为什么一定要是e指数才可以呢？其它的实数为什么不行呢，e的特殊性究竟再哪里呢？

对于a\in R

a^{it}=e^{lna^{it}}=e^{it\cdot lna}=cos(lna \cdot t)+i sin(lna\cdot t)

如果a=e

 则

e^{it}=e^{lne^{it}}=e^{it\cdot lne}=cos(lne \cdot t)+i sin(lne\cdot t)=cos(t)+isin(t)

恰好是欧拉公式，我们看一下当a=5, a=e, a=2的时候，运动图像会有什么不同:

从动图可以看出，A点在区间

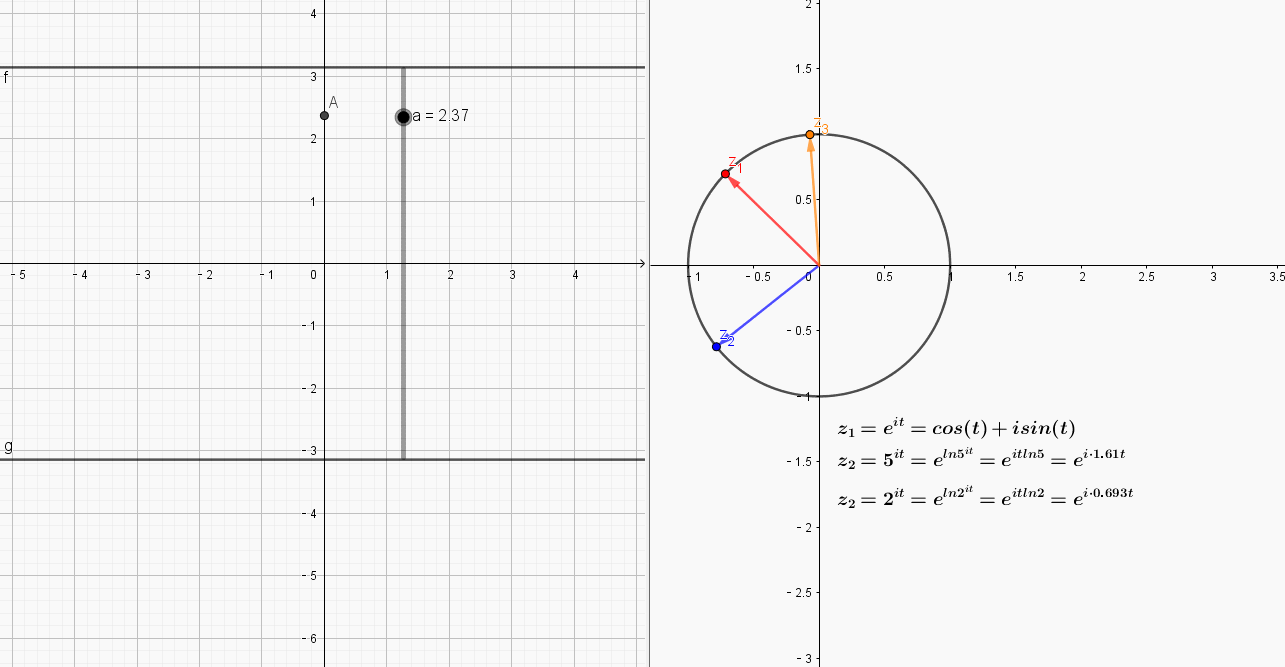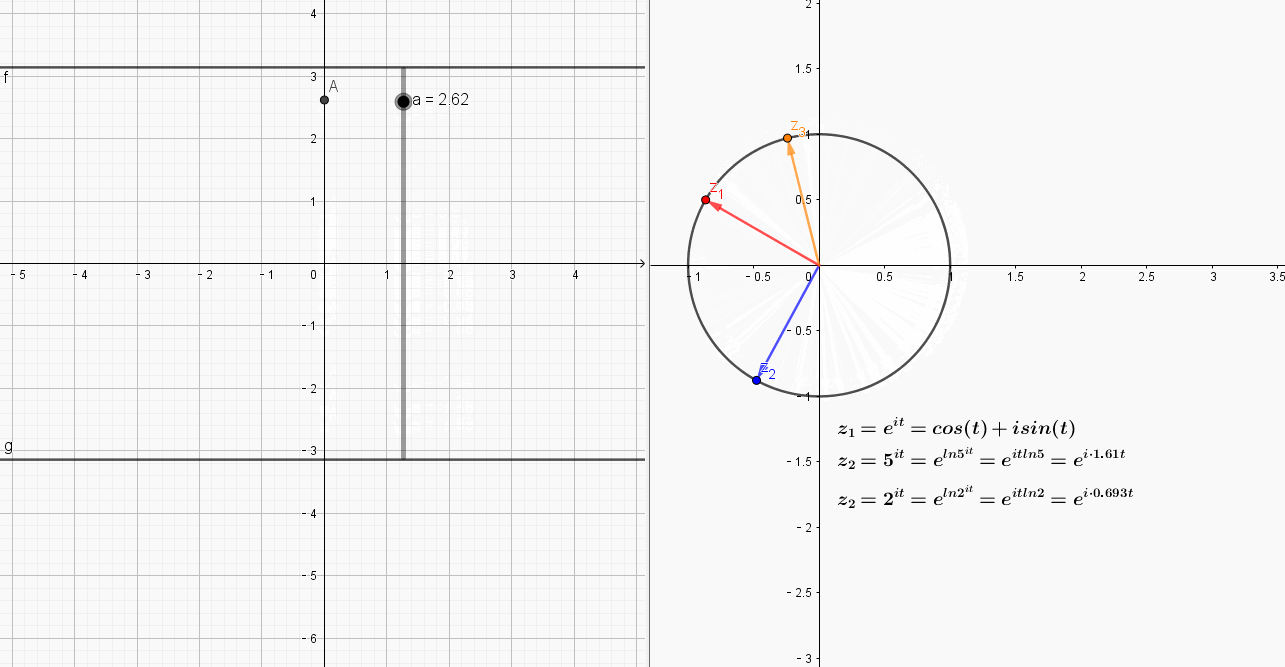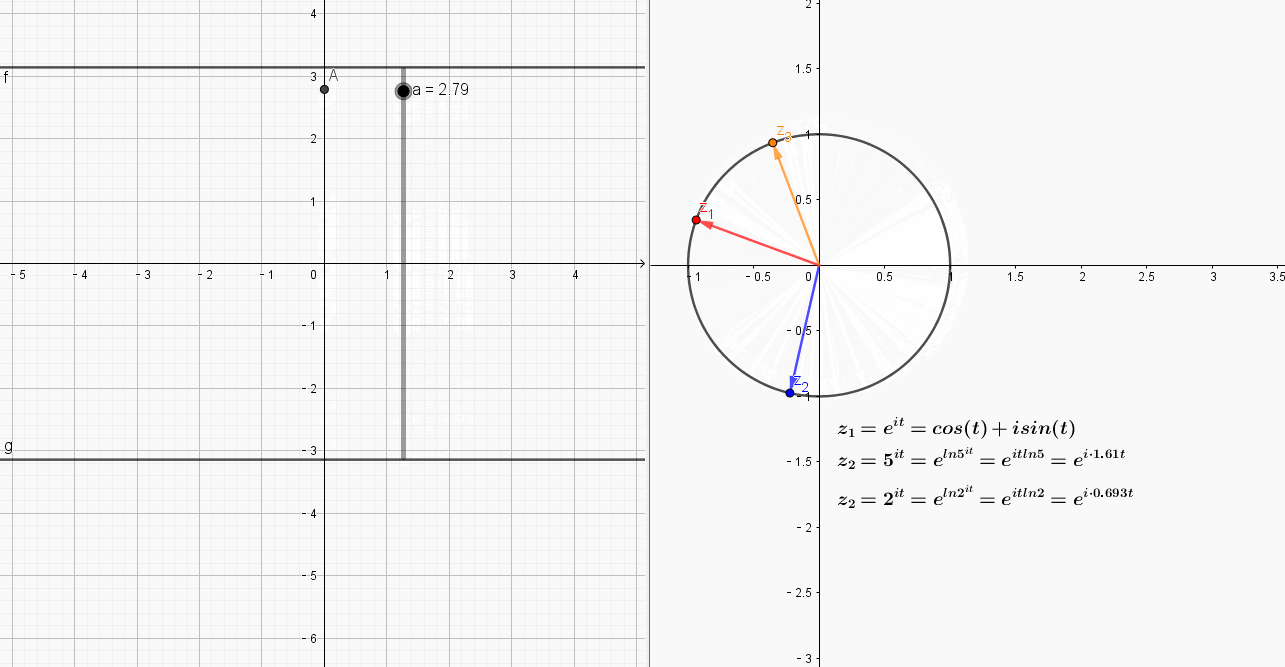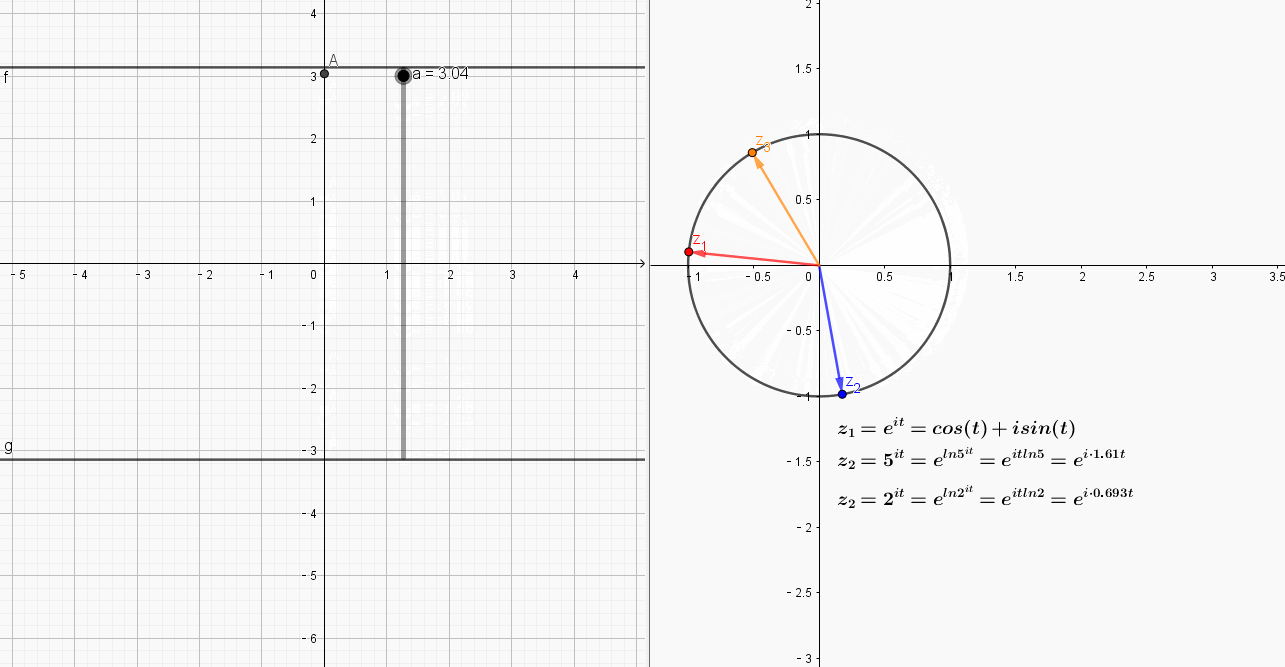
\bigg[-\pi, \pi \bigg]

运动时，只有z_1=e^{it}，也就是红色的向量，围绕原点运动了整整一圈,z_2由于角速度过大，围绕原点超过了１圈，而z_3则由于角速度过小，当自变量A变动一周后，像点运动不到一圈．

特别的，当A运动到\pi点时，z_1恰好运动到负实轴的-1，也就是

e^{-i\pi}=cos(\pi)+isin(\pi)=-1

就是号称世界上最美公式的欧拉公式！

如果指数用复数代替纯虚数，则可以写成

z=a+bi

f(z)=e^z=1+z+\frac{1}{2!}z^2+\frac{1}{3!}z^3+\frac{1}{4!}z^4+\cdots

下图表示当z=1+2i时，

e^z=e^{1+2i}=e\cdot e^{2i}=e(cos2+isin2)\mathbf{}

随着级数的增加，级数和螺旋式样收敛于 e圆上，其与远点的距离为e^a,角度为b弧度．对于z=1+2i的情况，2 弧度=114.59156 度，收敛于e圆上．实际上，这种曲线有一个专门的名字，叫做对数螺线，老鹰抓小鸡，飞蛾扑火，导弹追踪目标，走出的都是对数螺线的轨迹。

另一种推导

根据棣莫弗公式：

cos(\theta)+isin(\theta) = \big(cos(\frac{\theta}{n})+isin(\frac{\theta}{n})\big)^n=\bigg[cos(\frac{\theta}{n})\big(1+\frac{isin(\frac{\theta}{n})}{cos(\frac{\theta}{n})}\big)\bigg]^n

当n趋近于无穷大时：

\lim_{n \to\infty }\bigg[cos(\frac{\theta}{n})\big(1+\frac{isin(\frac{\theta}{n})}{cos(\frac{\theta}{n})}\big)\bigg]^n=[1+isin(\frac{\theta}{n})]^n=(1+\frac{i\theta}{n})^n=e^{i\theta}

不失为另一种有趣的证明方式。

扩展，关于e

银行复利与自然常数e之间的关系,我们拿1元到银行去存，存一年，年利息是100%,聪明的你一眼就得出年收入是2元,这实在太少了，我们拿到第二家银行去存，利息半年算一次,一年的收入就是2.25元,计算方法是：

(1+\frac{1}{2})^2=2.25

以此类推，一年内结算n次就是：

(1+\frac{1}{n})^n

典型的，如果一天一结算，就是：

(1+\frac{1}{365})^{365}\approx 1.72

这个值不是无限增大的，当n趋于无穷大时，会趋于某个稳定值，这个值就是e了，我们用图形画出来就是如下图所示：

根据函数图像也可以看出，当n趋向负无穷时，极限也是e,推算一下,下式x>0,则-x<0：

\\ y=(1-\frac{1}{x})^{-x}=\frac{1}{(1-\frac{1}{x})^{x}}=\frac{1^x}{(1-\frac{1}{x})^{x}}=\big(\frac{1}{1-\frac{1}{x}}\big)^x=\big(\frac{x}{x-1}\big)^x \\ =\big(\frac{x-1+1}{x-1}\big)^x=(1+\frac{1}{x-1})^x=(1+\frac{1}{x-1})^{x-1}\cdot (1+\frac{1}{x-1})=e\cdot 1=e

现在的数学刻本从高中到大学的教学方法是首先教授e指数函数的泰勒展开：

e^x=1+\frac{x}{1!} + \frac{x^2}{2!}+\cdots +\frac{x^n}{n!}+\cdots

然后经过微分学的学习之后偶然的，与任何学习经历无关的发现：

cos(x)=1-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}+(-1)^n\frac{x^{2n}}{(2n)!}+o(x^{2n+1})=\sum_{n=0}^{\infty }(-1)^n\frac{x^{2n}}{(2n)!}

sin(x)=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+(-1)^n\frac{x^{2n+1}}{(2n+1)!}+o(x^{2n+2})=\sum_{n=0}^{\infty }(-1)^n\frac{x^{2n+1}}{(2n+1)!}

而如果把：

e^x

中的x换成ix,联立两个级数，即可得到：

e^{ix}=1+i\frac{x}{1!} - \frac{x^2}{2!}-i\frac{x^3}{3!}+\frac{x^4}{4!}+i\frac{x^5}{5!}+\cdots +\frac{(ix)^n}{n!}+\cdots = cos(x) + i\cdot sin(x)

课本中是用这种毫不自然的方式介绍欧拉公式的，观点LOWB，跳跃太大，如果结合数形介绍，会效果会好很多。

参考资料

人人需要学习：银行复利与自然常数e之间的关系

结束！

相关文章