导航学说解密 飞蛾扑火现象
飞蛾扑火,自取灭亡。飞蛾为什么扑火啊?
今天我们就来讨论一下飞蛾扑火的问题。飞蛾扑火自取灭亡,它快到火的时候感觉到很热,它为什么不跑?这跟飞蛾的习性有关,火对飞蛾的吸引力非常强,究竟有多强?

昆虫学家做过一个实验:在一个屋子里边放了一只雌蛾,还放了一个篝火,然后让这个雄蛾飞进来。结果这个飞蛾朝篝火就过去了。有了火之后连雌蛾都不要了。就这么厉害,那么为什么飞蛾有这么强烈的对火的欲望?有一种说法就是飞蛾利用光来导航。这种导航说,现在科学界是比较公认的。这个在以前人类没有掌握火的技术和灯光的时候,在晚上飞蛾出行时只有星光和月光。星光和月光离我们非常遥远,所以近似认为是平行光线。那么飞蛾想飞,而且它希望能够飞直线,于是飞蛾在飞行的时候就希望自己的飞行路径能与这个光线成一个固定角度。比如说成30度角,它时时刻刻都与这个光线呈30度角,而光线是平行的,所以飞蛾飞行的就是直线。这就是飞蛾在飞行的时候利用光线来进行导航,就这么一个道理。

那么为什么现在飞蛾开始扑火了?是因为,现在人类已经掌握了火的技术,动不动给点把火或者是点个灯泡什么的。那么在这种情况下,这个光源可就不是无限远的!而是近处的光源,比如说有一个灯泡,它发的光是发散型的,并不是一个平行光线,那么飞蛾过来之后它不知道这事,它以为这个光线还是平行光线,于是飞蛾就按照自己的习性,它飞行方向与光线成固定角度。结果越飞越近,最后就撞到这个光源上了。

它在飞的时候总是保持这个固定角度,他以为自己飞的是直线,事实它却飞出一个旋来。就这么一个道理,它靠得特别特别近,想离开火的时候已经来不及了。因为他本性使然,就会沿着这样的一个路径走,它以为只要这样走就会走直线,实际上却不是这样的。就好比说咱们打个比方,人类行走在周围景物是不动的情况下,往前走的时候可以走直线,假如说在一个房间里,这个房间里所有其他的景物都在摇晃的话,想象一下你还能走直线吗?有些科技馆里就有这种东西,人是很难走直线的。那时候的人就变成了这里边的飞蛾了。飞蛾走出这个路径,大家知道叫什么曲线,这个曲线叫等角螺旋!

等角螺旋还有一个名字黄金螺旋。勒内·笛卡尔,法国的哲学家、数学家、物理学家。在1638年发现了这个曲线,研究出它的方程来了,然后就觉得它非常美,最典型的一件事就是它无法放大。
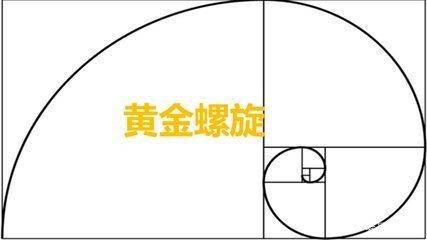

假如你把这个螺旋放大一倍,你会发现这个螺旋长得跟原先一模一样。这就是因为他这个螺旋是无限的,你放大了之后它的形状,你会发现这个曲线跟原来是完全重合的。笛卡尔看到这个曲线之后非常高兴,他就要求自己死了之后工匠把这个曲线刻在自己的墓碑上,而且还要写一句话叫“纵使改变依然故我”,这个就是笛卡尔的啊希望给自己定的墓志铭,但是最后很遗憾,工匠把这个螺旋画错了,画成了这个阿基米德螺旋或者叫等螺旋了。
其实飞蛾不想扑火的,只是导航出问题了,生活中大家也不要过于相信导航。
老鹰抓兔子,导弹打击目标也同样遵循对数螺线的规律。
在复平面上随便取一个复数z=a+bi, 那么z^n则是一个对数螺旋:
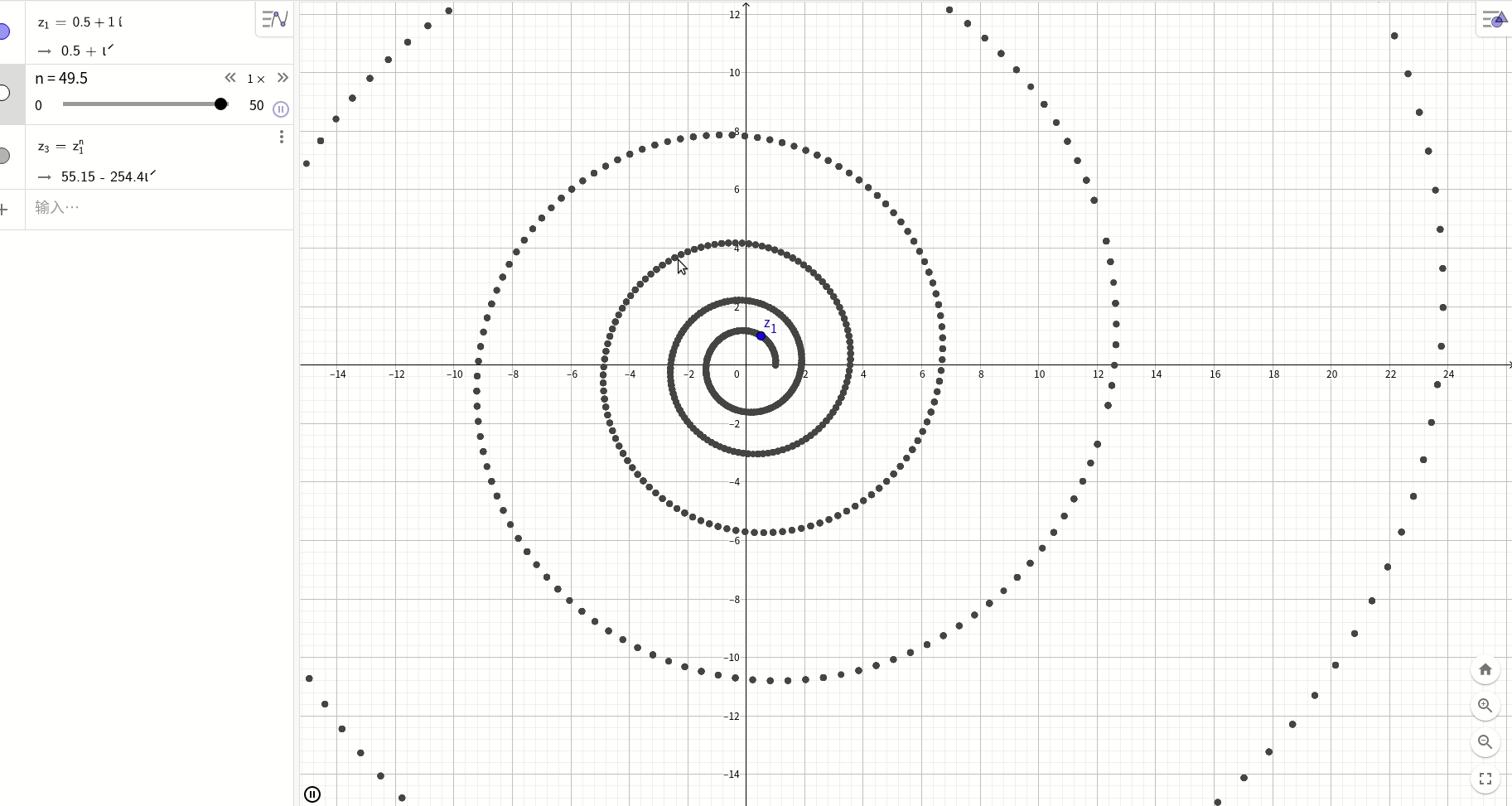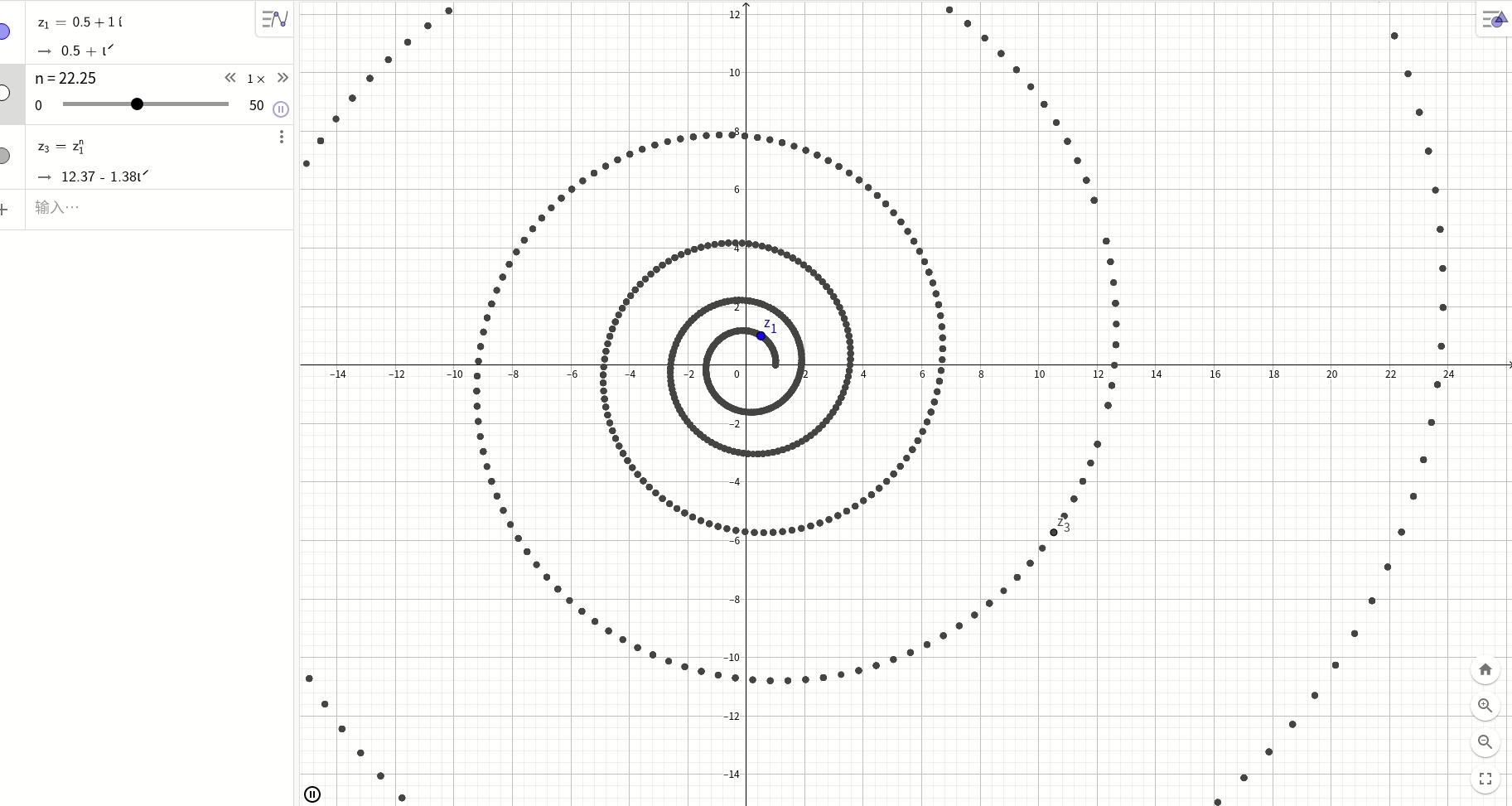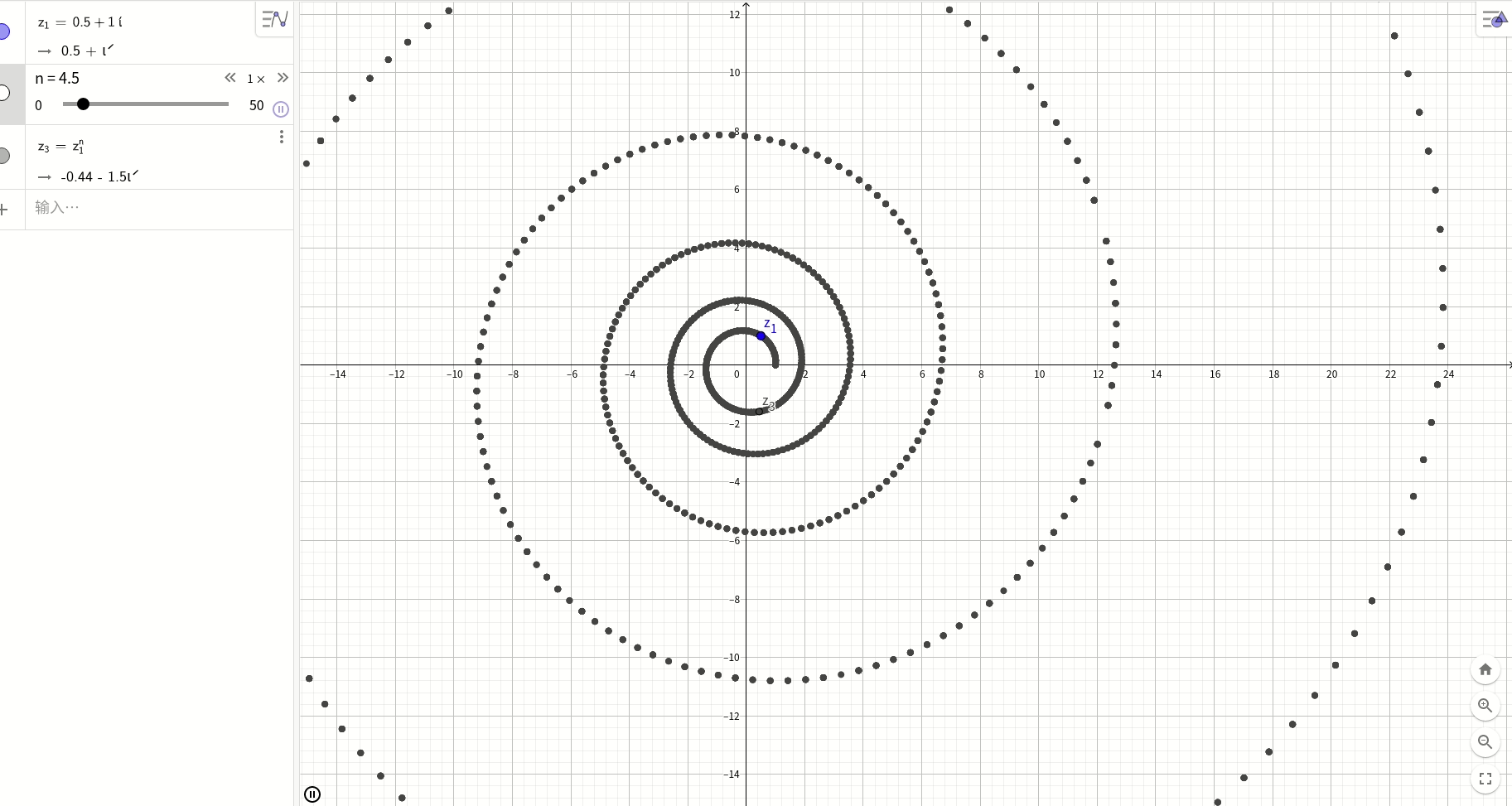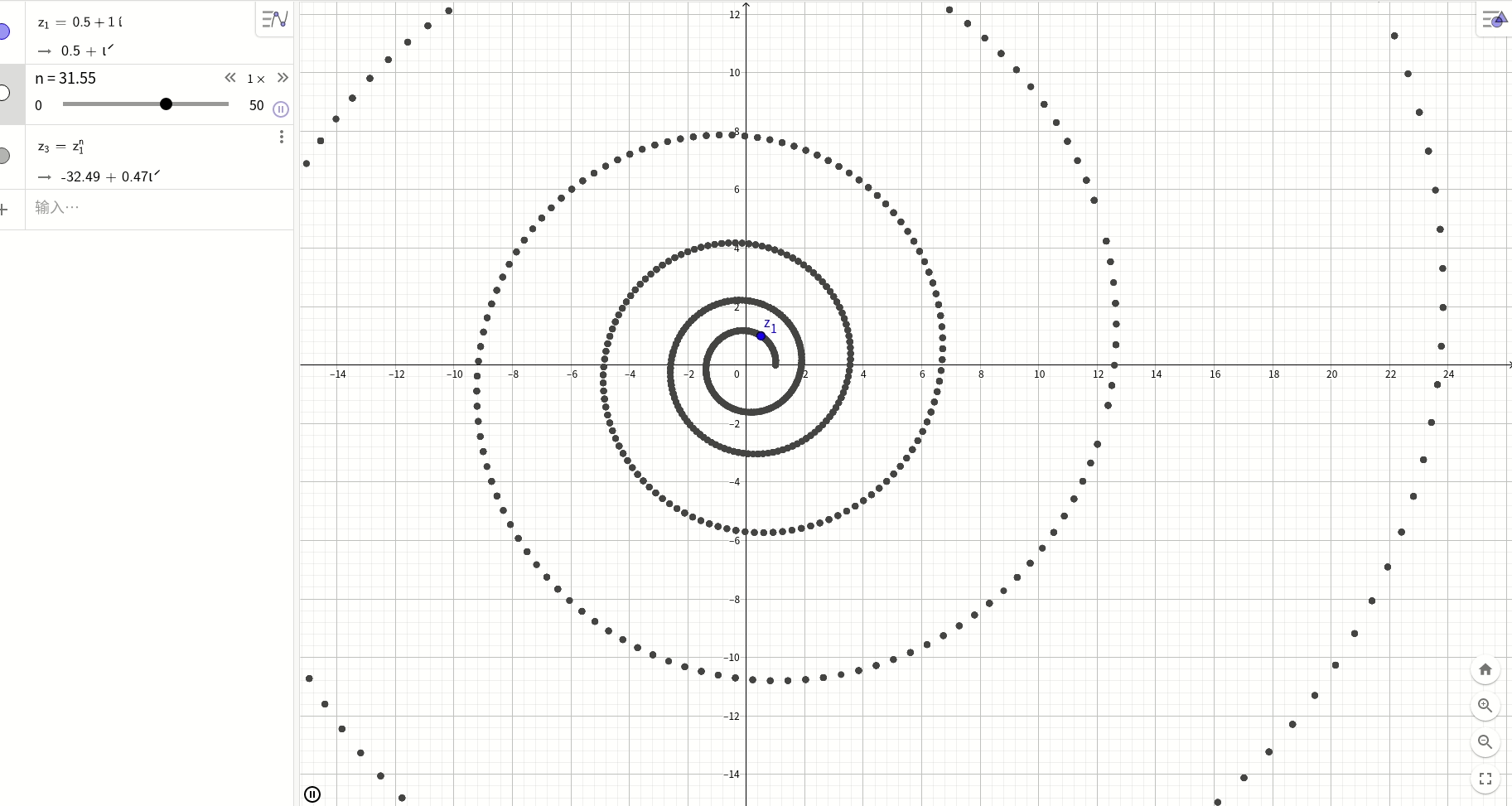
总结:
对数螺线是一根无止尽的螺线,它永远向着极绕,越绕越靠近极,但又永远不能到达极。据说,使用最精密的仪器也看不到一根完全的对数螺线,这种图形只存在科学家的假想中。 螺线特别是对数螺线的美学意义可以用指数的形式来表达: ρ=αe^(kφ) 其中,α和k为常数,φ是极角,ρ是极径,e是自然对数的底。为了讨论方便,我们把e或由e经过一定变换和复合的形式定义为“自然律”。因此,“自然律”的核心是e,其值为2.71828……,是一个无限不循环小数。 对数螺线在自然界中最为普遍存在,其它螺线也与对数螺线有一定的关系,不过目前我们仍未找到螺线的通式。


