题目

存在一个 无向图 ，图中有 n 个节点。其中每个节点都有一个介于 0 到 n - 1 之间的唯一编号。给你一个二维数组 graph ，其中 graph[u] 是一个节点数组，由节点 u 的邻接节点组成。形式上，对于 graph[u] 中的每个 v ，都存在一条位于节点 u 和节点 v 之间的无向边。该无向图同时具有以下属性：

• 不存在自环（graph[u] 不包含 u）。
• 不存在平行边（graph[u] 不包含重复值）。
• 如果 v 在 graph[u 内，那么 u也应该在 graph[v] 内（该图是无向图）
• 这个图可能不是连通图，也就是说两个节点 u 和 v 之间可能不存在一条连通彼此的路径。

二分图 定义：如果能将一个图的节点集合分割成两个独立的子集 A 和 B ，并使图中的每一条边的两个节点一个来自 A 集合，一个来自 B 集合，就将这个图称为 二分图 。

如果图是二分图，返回 true ；否则，返回 false 。

示例1：

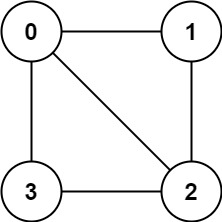
输入：graph = [[1,2,3],[0,2],[0,1,3],[0,2]]
输出：false
解释：不能将节点分割成两个独立的子集，以使每条边都连通一个子集中的一个节点与另一个子集中的一个节点。

示例2：

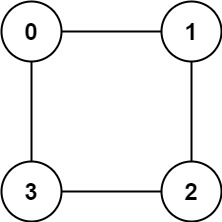
输入：graph = [[1,3],[0,2],[1,3],[0,2]]
输出：true
解释：可以将节点分成两组: {0, 2} 和 {1, 3} 。

提示：

• $graph.length==n$
• $1<=n<=100$
• $0<=graph[u].length<n$
• $0<=graph[u][i]<=n-1$
• $graph[u]$ 不会包含 $u$
• $graph[u]$ 的所有值 互不相同
• 如果 $graph[u]$ 包含 $v$，那么 $graph[v]$ 也会包含 $u$

题解

【前言】

对于图中的任意两个节点 $u$ 和 $v$，如果它们之间有一条边直接相连，那么 $u$ 和 $v$ 必须属于不同的集合。

如果给定的无向图连通，那么我们就可以任选一个节点开始，给它染成红色。随后我们对整个图进行遍历，将该节点直接相连的所有节点染成绿色，表示这些节点不能与起始节点属于同一个集合。我们再将这些绿色节点直接相连的所有节点染成红色，以此类推，直到无向图中的每个节点均被染色。

如果我们能够成功染色，那么红色和绿色的节点各属于一个集合，这个无向图就是一个二分图；如果我们未能成功染色，即在染色的过程中，某一时刻访问到了一个已经染色的节点，并且它的颜色与我们将要给它染上的颜色不相同，也就说明这个无向图不是一个二分图。

【算法的流程】

我们任选一个节点开始，将其染成红色，并从该节点开始对整个无向图进行遍历；

在遍历的过程中，如果我们通过节点 $u$ 遍历到了节点 $v$（即 $u$ 和 $v$ 在图中有一条边直接相连），那么会有两种情况：

• 如果 $v$ 未被染色，那么我们将其染成与 $u$ 不同的颜色，并对 $v$ 直接相连的节点进行遍历；
• 如果 $v$ 被染色，并且颜色与 $u$ 相同，那么说明给定的无向图不是二分图。我们可以直接退出遍历并返回 $\text{False}$ 作为答案。
• 当遍历结束时，说明给定的无向图是二分图，返回 $\text{True}$ 作为答案。

我们可以使用「深度优先搜索」或「广度优先搜索」对无向图进行遍历，下文分别给出了这两种搜索对应的代码。

注意：题目中给定的无向图不一定保证连通，因此我们需要进行多次遍历，直到每一个节点都被染色，或确定答案为 $\text{False}$为止。每次遍历开始时，我们任选一个未被染色的节点，将所有与该节点直接或间接相连的节点进行染色。

解法一：深度优先搜索

class Solution {
private:
    static constexpr int UNCOLORED = 0;
    static constexpr int RED = 1;
    static constexpr int GREEN = 2;
    vector<int> color;
    bool valid;
public:
    void dfs(int node, int c, const vector<vector<int>> &graph) {
        color[node] = c;
        int cNei = (c == RED ? GREEN : RED);
        for (int neighbor : graph[node]) {
            if (color[neighbor] == UNCOLORED) {
                dfs(neighbor, cNei, graph);
                if (!valid) return ;
            } else if (color[neighbor] != cNei) {
                valid = false;
                return ;
            }
        }
    }
    bool isBipartite(vector<vector<int>>& graph) {
        int n = graph.size();
        valid = true;
        color.assign(n, UNCOLORED);
        for (int i = 0; i < n && valid; i++) {
            if (color[i] == UNCOLORED) {
                dfs(i, RED, graph);
            }
        }
        return valid;
    }
};

【复杂度分析】

• 时间复杂度：$O(N+M)$，其中 $N$ 和 $M$ 分别是无向图中的点数和边数。
• 空间复杂度：$O(N)$，存储节点颜色的数组需要 $O(N)$ 的空间，并且在深度优先搜索的过程中，栈的深度最大为$N$，需要 $O(N)$ 的空间。

解法二：广度优先搜索

class Solution {
private:
    static constexpr int UNCOLORED = 0;
    static constexpr int RED = 1;
    static constexpr int GREEN = 2;
    vector<int> color;    
public:
    bool isBipartite(vector<vector<int>>& graph) {
        int n = graph.size();
        color.assign(n, UNCOLORED);
        for (int i = 0; i < n; i++) {
            if (color[i] == UNCOLORED) {
                queue<int> que;
                que.push(i);
                color[i] = RED;
                while (!que.empty()) {
                    int node = que.front();
                    int cNei = (color[node] == RED ? GREEN : RED);
                    que.pop();
                    for (int neighbor : graph[node]) {
                        if (color[neighbor] == UNCOLORED) {
                            que.push(neighbor);
                            color[neighbor] = cNei;
                        } else if (color[neighbor] != cNei) {
                            return false;
                        }
                    }
                }
            }
        }
        return true;
    }
};

【复杂度分析】

• 时间复杂度：$O(N+M)$，其中 $N$ 和 $M$ 分别是无向图中的点数和边数。
• 空间复杂度：$O(N)$，存储节点颜色的数组需要 $O(N)$ 的空间，并且在广度优先搜索的过程中，队列中最多有 $N-1$ 个节点，需要 $O(N)$ 的空间。

解法三：并查集

【思路】

根据二分图的定义，一条边上的两个点要在不同的集合中。于是遍历图中的每个点，将该点的所有邻接点进行合并，如果邻接的点中有与当前点在同一个集合中，则该图不是二分图。

【代码】

class UnionSet {
private:
    vector<int> parent;
    vector<int> rank;
public:
    UnionSet(int n) {
        parent.resize(n);
        rank.resize(n);
        for (int i = 0; i < n; i++) {
            parent[i] = i;
            rank[i] = 1;
        }
    }

    int find(int u) {
        return parent[u] == u ? u : parent[u] = find(parent[u]);
    }

    bool isConnected(int u, int v) {
        return find(u) == find(v);
    }

    void merge(int u, int v) {
        int pu = find(u), pv = find(v);
        if (pu == pv) return ;
        if (rank[pu] < rank[pv]) {
            parent[pu] = pv;
            rank[pv] += rank[pu];
        } else {
            parent[pv] = pu;
            rank[pu] += rank[pv];
        }
    }
};

class Solution {
public:
    bool isBipartite(vector<vector<int>>& graph) {
        UnionSet us(graph.size());
        for (int i = 0; i < graph.size(); i++) {
            for (int j = 0; j < graph[i].size(); j++) {
                //判断与i点邻接的点是否与i点在同一个集合中
                //若在同一集合中，则直接返回false
                if (us.isConnected(graph[i][j], i)) return false;
                //若不在同一集合中，则将邻接点进行合并,注意：合并的是邻接点，而不是该点与邻接点进行合并
                us.merge(graph[i][0], graph[i][j]);
            }
        }
        return true;
    }
};

【复杂度分析】

• 时间复杂度：$O(m+n)$，其中 $m$ 和 $n$ 分别是无向图的点数和边数。
• 空间复杂度：$O(m)$， 其中 $m$ 是无向图的点数。