【Neo4j】第 4 章:图形数据科学Library and Path Finding
🔎大家好,我是Sonhhxg_柒,希望你看完之后,能对你有所帮助,不足请指正!共同学习交流🔎
📝个人主页-Sonhhxg_柒的博客_CSDN博客 📃
🎁欢迎各位→点赞👍 + 收藏⭐️ + 留言📝
📣系列专栏 - 机器学习【ML】 自然语言处理【NLP】 深度学习【DL】
🖍foreword
✔说明⇢本人讲解主要包括Python、机器学习(ML)、深度学习(DL)、自然语言处理(NLP)等内容。
如果你对这个系列感兴趣的话,可以关注订阅哟👋
文章目录
在本章中,我们将首次使用Graph Data Science ( GDS ) 库,它是 Neo4j 的 Graph Algorithm 库的继承者。在介绍了该库的主要原理之后,我们将了解寻路算法。之后,我们将使用Python 和 Java中的实现来了解它们是如何工作的。然后我们将学习如何使用这些算法的优化版本,在 GDS 插件中实现。我们将介绍Dijkstra 和 A* 最短路径算法,以及其他与路径相关的方法,例如旅行商问题和最小生成树。
本章将涵盖以下主题:
- 介绍图形数据科学插件
- 通过其应用了解最短路径的重要性
- 通过 Dijkstra 的最短路径算法
- 使用 A* 算法及其启发式查找最短路径
- 在 GDS 库中发现其他与路径相关的算法
- 使用图表优化我们的流程
技术要求
本章将使用以下工具:
- Neo4j (≥ 3.5) 与 Neo4j Graph Data Science ≥ 1.0 插件
- 部分代码示例将使用 Python 编写(推荐 ≥ 3.6)
- 使用的完整代码文件位于:
https ://github.com/PacktPublishing/Hands-On-Graph-Analytics-with-Neo4j/ch4/
如果您使用的是Neo4j < 4.0,那么GDS插件的最新兼容版本是1.1, 而如果您使用的是Neo4j ≥ 4.0,那么GDS插件的第一个兼容版本是1.2。
介绍图形数据科学插件
我们将从介绍 GDS 插件开始。由 Neo4j 提供,它扩展了其图形数据库的功能以用于分析目的。在本节中,我们将介绍命名约定并介绍非常重要的图形投影概念,我们将在本书的其余部分集中使用它。
该插件的第一个实现是在 2017 年 6 月首次发布的图形算法库中完成的。2020 年,它被 GDS 插件所取代。GDS 插件包括对最常用算法的性能优化,以便它们可以在巨大的图(数十亿个节点)上运行。尽管我将重点介绍本书中的优化算法,但我建议您参考最新的文档以确保您获得最新的信息(https://neo4j.com/docs/graph-data-science /当前/)。
使用自定义函数和过程扩展 Neo4j
在前面的章节中,我们实际上已经使用了几个 Neo4j 扩展。APOC 和 neo4j-nlp 都是使用 Neo4j 提供的工具构建的,用于从外部库访问核心数据库。Neo4j 在其 3.0 版本中开始提供此功能。
用户有机会定义自定义功能和/或程序。我们先来了解一下这两类对象的区别。
过程和函数的区别
函数和过程之间的主要区别在于每行返回的结果数。函数必须每行返回一个且仅返回一个结果,而过程可以返回更多值。
功能
要获取正在运行的 Neo4j 实例中的可用函数列表,您可以使用以下命令:
CALL dbms.functions()默认安装(不带插件)已经包含一些函数——例如,randomUUID函数。
函数的结果可以通过正常的 Cypher 查询访问。例如,要生成随机 UUID,您可以使用以下命令:
RETURN randomUUID()这可用于在创建这样的节点时生成随机 UUID:
CREATE (:Node {uuid: randomUUID()})将使用uuid包含随机生成的 UUID 的属性创建一个新节点。
程序
可以使用以下查询获得可用过程的列表:
CALL dbms.procedures()要调用一个过程,我们必须使用CALL关键字。
例如,db.labels是一个在默认安装中可用的过程。通过使用以下查询,您将看到活动图中使用的标签列表:
CALL db.labels()由于它返回多行,因此不能像randomUUID设置节点属性的函数那样使用它。这就是为什么它是一个过程而不是一个函数。
在 Neo4j 中编写自定义函数
如果您有兴趣编写自己的自定义过程,Neo4j 为此提供了一个 Java API。在 Maven 项目中,您必须包含以下依赖项:
<dependency>
<groupId>org.neo4j</groupId>
<artifactId>neo4j</artifactId>
<version>${neo4j.version}</version>
<scope>provided</scope>
</dependency>可以使用以下代码实现简单地将两个数字相乘的用户定义函数:
@UserFunction
@Description("packt.multiply(value, value)")
public Double multiply(
@Name("number1") Double number1,
@Name("number2") Double number2
) {
if (number1 == null || number2 == null) {
return null;
}
return number1 * number2;
}让我们分解这段代码:
- @UserFunction注解声明了一个用户定义的函数。类似地,可以使用@Procedure注解声明过程。
- 然后我们声明一个名为 的函数multiply,返回类型为Double。它接受两个参数:( number1)Double和number2( Double)。
- 如果这些数字中的任何一个为 null,则该函数返回 null,否则,它返回两个数字的乘积。
在构建项目并将生成的 JAR 复制到我们图的 plugins 目录后,我们将能够使用这个新功能,如下所示:
RETURN packt.multiply(10.1, 2)现在让我们关注 GDS 插件。
GDS 库内容
GDS 插件包含几种类型的算法。在本章中,我们将专注于最短路径算法,但在后面的章节中,我们还将学习如何执行以下操作:
- 测量节点重要性:我们为此使用的算法称为中心性算法。例如,它们包括 Google 开发的用于对搜索结果进行排名的 PageRank 算法(参见第 5 章,节点重要性)。
- 识别节点社区(参见第 7 章,社区检测和相似性度量)。
- 提取特征以执行链接预测(参见第 9 章,预测关系)。
- 运行图嵌入算法以从图结构中学习特征(参见第 10 章,图嵌入——从图到矩阵)。
过程的名称有一个共同的语法:
gds.<tier>.<algo>.<write|stream>(graphName, configuration)让我们详细看看每个组件:
- tier是可选的。如果过程名称不包含tier,则表示该算法完全受支持并且具有生产就绪的实现。其他可能的值为alpha或beta。该alpha层包含从图形算法库移植的算法,但尚未优化。
- algo是算法名称,例如shortestPath.
- write | stream允许您控制结果的呈现方式(下一节将详细介绍)。
- graphName是算法将在其上运行的投影图的名称。
- configuration是定义算法参数的映射。
configuration我们将在地图中详细介绍我们将在本书中学习的每种算法的可用选项。但在此之前,我们需要了解投影图是什么。
要查找过程的确切名称,可以使用以下查询:
CALL gds.list() YIELD name, description, signature
WHERE name =~ ".*shortestPath.*"
RETURN name, description, signature定义投影图
在实践中,大多数时候,您不想在完整的 Neo4j 图上运行 GDS 算法。您可以通过在特定情况下选择您感兴趣的节点和关系来减少算法中使用的数据的大小。GDS 插件为此目的实现了投影图 概念。
投影图是 Neo4j 图的轻量级版本,仅包含节点、关系和属性的子集。减小图形的大小使其能够适应 RAM,从而使访问更容易和更快。
我们可以使用为会话长度定义的命名投影图,或在运行算法时动态定义的匿名投影图。虽然这不是强制性的,但我们在本书中将主要使用命名投影图,它允许我们拆分投影图定义和算法配置。
投影图是高度可定制的。您可以选择特定标签和类型,重命名它们,甚至创建新标签。
原生投影
创建投影图的第一种方法是列出要包含的节点标签、关系类型和属性。为此,我们将使用该gds.graph.create过程来创建一个命名的投影图。其签名如下:
CALL gds.graph.create(
graphName::STRING,
nodeProjection::STRING, LIST or MAP,
relationshipProjection::STRING, LIST or MAP,
configuration::MAP
)使用此过程的最简单方法是包含所有节点和关系,如下所示:
CALL gds.graph.create("projGraphAll", "*", "*")该projGarphAll图现在可用,我们将能够告诉图算法在该图上运行。
如果您需要更多自定义,这里是节点投影的完整签名:
{
<node-label>: {
label: <neo4j-label>,
properties: {
<property-key-1>: {
property: <neo-property-key>,
defaultValue: <numeric-value>
},
[...]
}
},
[...]
}以下节点投影包括具有User标签和name属性的节点。如果给定节点缺少该属性,则使用空字符串代替(默认值):
{
"User": {
label: "User",
properties: {name: {property: "name", defaultValue: ""}}
}
}同样,关系投影定义如下:
{
<relationship-type>: {
type: <neo4j-type>,
projection: <projection-type>,
aggregation: <aggregation-type>,
properties: {
<property-key-1>: {
property: <neo4j-property-key>,
defaultValue: <numeric-value>,
aggregation: <aggregation-type>
},
[...]
}
},
[...]
}幸运的是,当我们不想重新定义一切时,捷径是可能的。例如,要选择带有 User 标签的所有节点以及带有类型的所有关系FOLLOWS,可以使用以下命令:
CALL gds.graph.create("myProjectedGraph", "User", "FOLLOWS")此语法已经允许对要包含在投影图中的对象进行大量自定义。如果这还不够,还可以通过 Cypher 查询定义投影图,正如我们现在将讨论的那样。
Cypher projections
为了进一步自定义投影图,您可以使用 Cypher 投影。它使我们能够动态创建仅在投影图中而不是在 Neo4j 图中创建的关系。创建投影图的语法与原生投影图语法非常相似,只是节点和关系的配置是通过 Cypher 查询完成的:
CALL gds.graph.create.cypher(
graphName::STRING,
nodeQuery::STRING,
relationshipQuery::STRING,
configuration::MAP
)唯一的限制如下:
- nodeQuery必须返回一个名为 的属性id,其中包含一个节点唯一标识符。
- relationshipQuery必须包含两个属性source和destination,指示源节点和目标节点标识符。
与 Cypher 投影的等价物myProjectedGraph如下:
CALL gds.graph.create.cypher(
"myProjectedCypherGraph",
"MATCH (u:User) RETURN id(u) as id",
"MATCH (u:User)-[:FOLLOWS]->(v:User) RETURN id(u) as source, id(v) as destination"
)Cypher投影对于在投影图中动态添加关系或属性非常有用。我们将在本书后面看到这个特性的几个例子(第 5 章,空间数据和第 8 章,在机器学习中使用基于图形的特征)。
将结果流式传输或写回图表
一旦我们定义了我们的图算法过程的输入,投影图,我们还必须决定插件将如何处理结果。有三种可能的选择:
- 流式传输结果:结果将以流的形式提供,可以在 Neo4j 浏览器中使用,也可以从 Neo4j 驱动程序以不同语言(Java、Python、Go、.NET 等)读取。
- 将结果写入 Neo4j 图:如果受影响的节点数量非常大,则流式传输结果可能不是一个好的选择。在那种情况下,可以将算法的结果写入初始图中;例如,向受影响的节点添加属性或添加关系。
- 改变投影图:算法结果作为新属性保存在内存图中。稍后必须使用该gds.graph.writeNodeProperties过程将它们复制到 Neo4j 图表中。
在本书中,我们将使用流或写入模式处理静态投影图。下图总结了完整的流水线: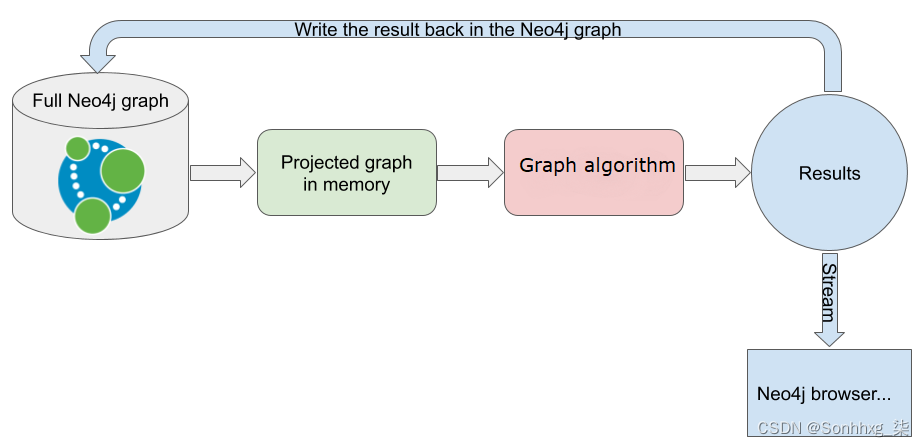
这两种返回模式之间的选择是通过过程名称进行的:
- gds.<tier>.<algo>.stream获得流式传输的结果
- gds.<tier>.<algo>.write将结果写回原始图中
牢记 GDS 的所有原则,我们可以继续我们的第一个用例:最短路径算法。在进入实现细节之前,让我们回顾一下寻路算法的一些应用,包括(但不限于)路由应用。
通过应用了解最短路径算法的重要性
当试图在图上寻找最短路径查找器的应用时,我们会想到通过 GPS 进行的汽车导航,但还有更多用例。本节概述了寻路的不同应用。我们将讨论网络和视频游戏,并介绍旅行商问题。
网络内的路由
路由通常是指 GPS 导航,但一些更令人惊讶的应用也是可能的。
GPS
GPS这个名称实际上用于两种不同的技术:
- 全球定位系统( GPS )本身就是一种在地球上找到精确位置的方法。它是通过围绕地球运行并发送连续信号的卫星星座来实现的。根据您的设备接收到的信号,基于三角测量方法的算法可以确定您的位置。
- 路由算法:根据您的位置和目的地的位置,对您周围的道路有充分了解的算法应该计算从您的位置 A 点到您的目的地 B 点的最短路线。
由于图表,这里的第二个要点成为可能。正如我们在第 1 章“图数据库”中所讨论的,道路网络是图的完美应用,其中交汇点是图的顶点(节点),它们之间的路段是边。本章将讨论最短路径算法,在下一章(第 5 章,空间数据)中,我们将创建一个路由引擎。
社交网络中的最短路径
在社交网络中,两个人之间的最短路径称为分离度。研究分离度的分布可以深入了解网络的结构。
其他应用
与图的情况一样,寻路算法在现实世界中有很多应用。以下部分是有趣的用例的两个示例,但在不同领域可以找到更多示例。
视频游戏
图表在视频游戏中经常使用。游戏环境可以建模为一个网格,而网格又可以看作是一个图,其中每个单元格是一个节点,相邻单元格通过一条边连接。在该图中查找路径允许玩家在环境中移动,避免与障碍物发生碰撞。
科学
图内寻路的一些应用已经在多个科学领域进行了研究,特别是遗传学,研究人员研究给定序列中基因之间的关系。
您可能会想到您专业领域中的其他应用程序。
现在让我们关注最著名的最短路径算法,Dijkstra 算法。
Dijkstra 的最短路径算法
Dijkstra 的算法是由荷兰计算机科学家 EW Dijkstra 在 1950 年代开发的。它的目的是找到图中两个节点之间的最短路径。第一部分将指导您了解算法的工作原理。第二小节将专门介绍在 Neo4j 和 GDS 插件中使用 Dijkstra 算法。
理解算法
Dijkstra 算法可能是最著名的寻路算法。它是一种贪心算法,会先遍历图的宽度(见下图),从给定节点(起始节点)开始,并尝试在每一步做出关于最短路径的最优选择: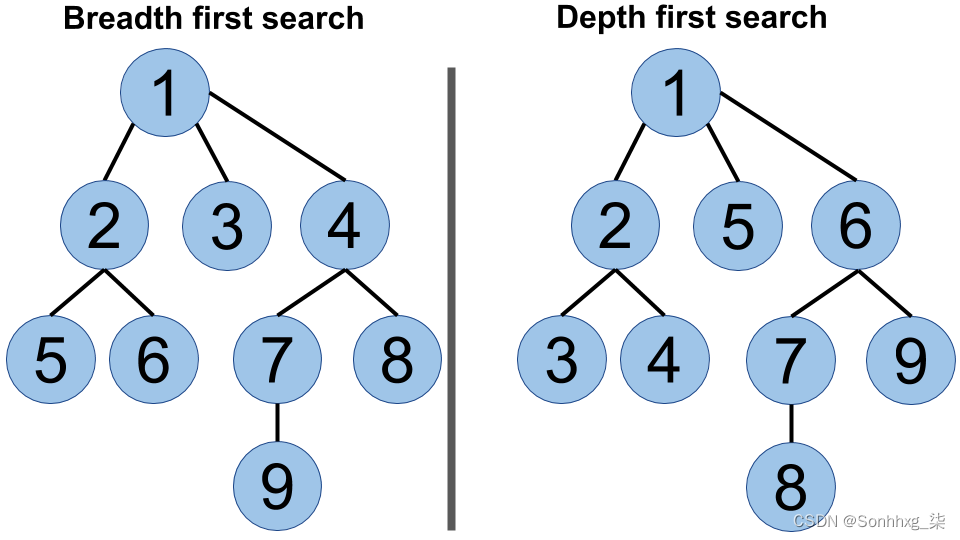
为了理解算法,让我们在一个简单的图上运行它。
在简单图上运行 Dijkstra 算法
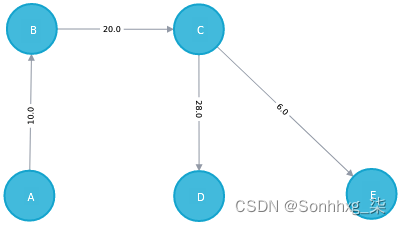
例如,我们将使用以下无向加权图:
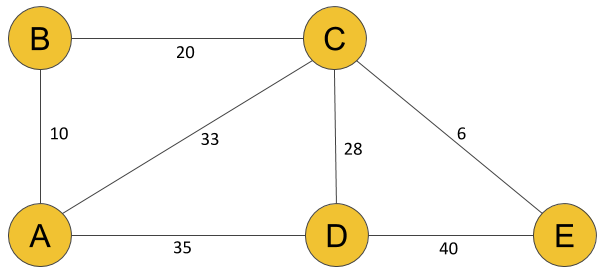
我们正在寻找节点A和E之间的最短加权路径。
不同的步骤如下:
- 初始化(表的第一行):我们将起始节点A与所有其他节点之间的距离初始化为无穷大,但从A到A的距离设置为 0。
- 第一次迭代(下表的第二行):
- 从节点A开始,算法将图遍历到A、B、C和D的每个邻居。
- 它记住从起始节点A到其他每个节点的距离。如果我们只对最短路径长度感兴趣,我们只需要距离。但是如果我们还想知道最短路径由哪些节点组成,我们还需要保留有关传入节点(父节点)的信息。在接下来的迭代中,原因将变得更加清晰。在本次迭代中,由于我们从节点A开始,所有计算的距离都是相对于节点A 的。
- 该算法选择到目前为止最接近A 的节点。在第二次迭代中,它从这个新的起始节点执行相同的操作。在这种情况下,B是最接近A的节点,因此第二次迭代将从B开始。
- 第二次迭代:从B开始,算法访问C——它唯一尚未在算法的任何迭代中用作起始节点的邻居。A到C经B的距离如下:
10 (A -> B) + 20 (B -> C) = 30这意味着从A到C通过B而不是直接从A到C更短。然后算法记住从A到C的最短路径是 30 并且到达C之前的前一个节点是B。换句话说,C的父级是B。
- 第三次迭代:在第三次迭代中,算法将从节点C开始,该节点距离上一次迭代最近的节点A,距离为 30。它访问D和E。从A到D通过C的距离为 58,高于从A到C的直接距离,因此不记忆这条新路径。
- 第四次迭代:第四次迭代从D开始,只访问节点E,这是唯一剩下的节点。同样,这是我们第二次在遍历中看到节点E,但似乎从C到达E的路径比从D的路径短得多,因此算法只会记住通过C的路径。
下表说明了所采取的步骤:
| Iteration | Start | A | B | C | D | E | Next node |
| 0 | A | 0 | ∞ | ∞ | ∞ | ∞ | A |
| 1 | A | x | 10 - A | 33 - A | 35 - A | ∞ | B |
| 2 | B | x | x | 33 - A 30 (10+20) - B | 35 - A | ∞ | C |
| 3 | C | x | x | x | 35 - A 58 (30+28) - C | 36 (30+4) - C | D |
| 4 | D | x | x | x | x | 36 (30+4) - C 75 (35+40) - D | E |
下图说明了相同的算法: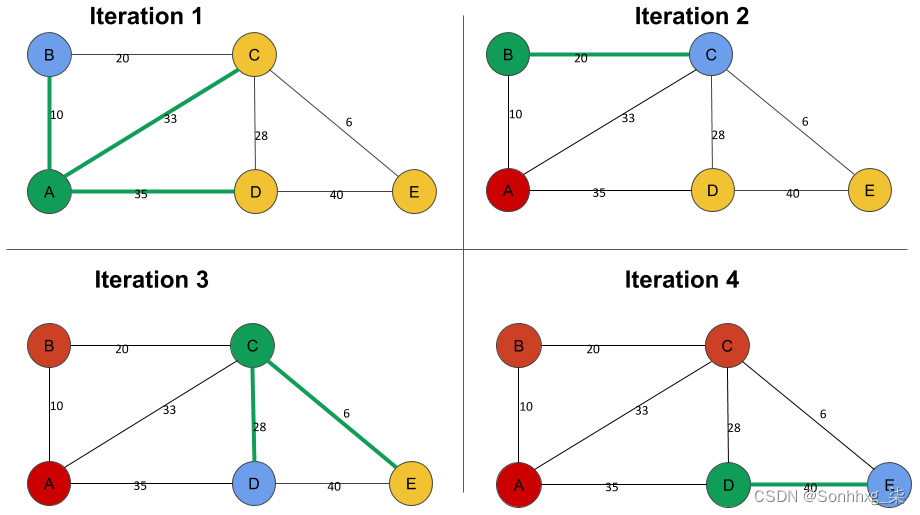
绿色节点代表每次迭代的起始节点。红色节点是已经访问过的节点,蓝色节点是将被选为下一次迭代的起始节点的节点。
我们现在已经研究了初始图中的所有节点。让我们回顾一下结果。为此,我们将从结束节点E开始。E列告诉我们从A到E的最短路径的总距离为 36。为了重建完整路径,我们必须按以下方式导航表:
- 从E列开始,我们寻找路径最短的行,并确定路径中的前一个节点:C。
- 我们从C列重复同样的操作:我们可以看到从A到C的最短路径是 30,这条路径中的前一个节点是B。
- 最后,我们可以从B列重复相同的过程,得出A和B之间的最短路径是直接路径,其成本为 10。
综上所述,A和E之间的最短路径如下:
A -> B -> C -> E
下一节给出了这个算法在纯 Python 中的示例实现。
示例实现
为了完全理解该算法,我们将看一个 Python 中的示例实现。
图形表示
首先,我们必须定义一个结构来存储图形。可以通过多种方式表示图形以执行计算。就我们的目的而言,最简单的方法是使用以图形节点为键的字典。与每个键关联的值包含另一个字典,表示从该节点开始的边及其相应的权重。例如,我们在本章学习的图可以写成如下:
G = {
'A': {'B': 10, 'C': 33, 'D': 35},
'B': {'A': 10, 'C': 20},
'C': {'A': 20, 'B': 33, 'D': 28, 'E': 6},
'D': {'A': 35, 'C': 28, 'E': 40},
'E': {'C': 6, 'D' : 40},
}这意味着顶点A 连接到其他三个顶点:
- B, 权重 10
- C, 重量 33
- D, 重量 35
此结构将用于在图形中导航以找到A和E之间的最短路径。
算法
以下代码重现了我们在上一节中遵循的步骤。
给定一个图 ,G该shortest_path函数将遍历该图以找到起点和终点节点之间的最短路径。
从 开始的每次迭代step_start_node都将执行以下操作:
- 找到 的邻居step_start_node。
- 对于每个邻居, (如果已经访问过,则n 跳过)执行以下操作:n
- 计算 和 之间的距离,n并step_start_node使用与 和 之间的边相关的权n重step_start_node。
- 如果新距离比之前保存的距离短(如果有),则将距离和传入(父)节点保存到shortest_distances字典中。
- 添加step_start_node到访问节点列表。
- step_start_node下一次迭代的更新:
- 下一次迭代将从最接近start_node 尚未访问的节点开始。
- 重复直到end_node被标记为已访问。
代码应如下所示:
def shortest_path(G, start_node, end_node):
"""Dijkstra 算法示例实现
:param dict G: 图形表示
:param str start_node: 起始节点名
:param str end_node: 结束节点名
"""
# 初始化shortest_distances到所有节点到 Infinity
shortest_distances = {k: (float("inf"), None) for k in G}
# 已经访问过的节点列表
visited_nodes = []
# 到起始节点的最短距离为0 shortest_distances
shortest_distances[start_node] = (0, start_node)
# 第一次迭代从 start_node 开始
step_start_node = start_node
while True:
print("-"*20, "Start iteration with node", step_start_node)
# 中断条件:当算法到达end_node
if step_start_node == end_node:
#return shortest_distances[end_node][0]
return nice_path(start_node, end_node, shortest_distances)
# 遍历当前 step_start_node 的所有直接邻居
for neighbor, weight in G[step_start_node].items():
# 如果邻居已经访问过,什么也不做
print("-"*10, "Neighbor", neighbor, "with weight", weight)
if neighbor in visited_nodes:
print("\t already visited, skipping")
continue
# 否则,将之前的距离与该节点进行比较
previous_dist = shortest_distances[neighbor][0]
# 通过 step_start_node 与新距离进行比较
new_dist = shortest_distances[step_start_node][0] + weight
# 如果新距离比之前的更短
# 记住新路径
if new_dist < previous_dist:
shortest_distances[neighbor] = (new_dist, step_start_node)
print("\t found new shortest path between", start_node, "and", neighbor, ":", new_dist)
else:
print("\t distance", new_dist, "higher than previous one", previous_dist, "skipping")
visited_nodes.append(step_start_node)
unvisited_nodes = {
node: shortest_distances[node][0] for node in G if node not in visited_nodes
}
step_start_node = min(unvisited_nodes, key=unvisited_nodes.get)我们可以使用上一节中定义的图形来使用这个函数:
shortest_path(G, "A", "E")这会产生以下输出:
==================== Start ====================
-------------------- Start iteration with node A
---------- Neighbors B with weight 10
found new shortest path between A and B : 10
---------- Neighbors C with weight 33
found new shortest path between A and C : 33
---------- Neighbors D with weight 35
found new shortest path between A and D : 35
-------------------- Start iteration with node B
---------- Neighbors A with weight 10
already visited, skipping
---------- Neighbors C with weight 20
found new shortest path between A and C : 30
-------------------- Start iteration with node C
---------- Neighbors A with weight 20
already visited, skipping
---------- Neighbors B with weight 33
already visited, skipping
---------- Neighbors D with weight 28
distance 58 higher than previous one 35 skipping
---------- Neighbors E with weight 6
found new shortest path between A and E : 36
-------------------- Start iteration with node D
---------- Neighbors A with weight 35
already visited, skipping
---------- Neighbors C with weight 28
already visited, skipping
---------- Neighbors E with weight 40
distance 75 higher than previous one 36 skipping
-------------------- Start iteration with node E
=============== Result ===============
36
==================== End ====================因此,我们找到了 36 的最短路径长度,这与我们的手动方法一致。
A如果我们需要的不仅仅是to的距离E,例如这条最短路径内的节点,我们可以从shortest_distances字典中检索此信息。
显示从 A 到 E 的完整路径
该变量在函数shortest_distances末尾包含以下数据:shortest_path
{
'A':(0,'A'),
'B':(10,'A'),
'C':(30,'B'),
'D':(35,'A'),
' E': (36, 'C')
}A我们可以使用这些信息很好地显示和之间的完整路径E。从结束节点开始,E,shortest_distances["E"][1]包含最短路径中的前一个节点。同理,包含从到到shortest_distances["C"][1]的最短路径中的前一个节点,以此类推。AE
我们可以编写以下函数来检索路径中的每个节点和距离:
def nice_path(start_node, end_node, shortest_distances):
node = end_node
result = []
while node != start_node:
result.append((node, shortest_distances[node][0]))
node = shortest_distances[node][1]
result.append((start_node, 0))
return list(reversed(result))此函数返回以下结果:
=============== Result ===============
[('A', 0), ('B', 10), ('C', 30), ('E', 36)]
==================== End ====================这些结果与我们在上一节中填写表格时发现的结果一致。
创建此实现是为了让您了解算法背后的原理。如果您打算将此算法用于实际应用程序,则存在最先进的库,在内存使用方面具有更优化的解决方案。在 Python 中,主图形库称为networkx:https ://networkx.github.io 。但是,使用此库或存储在 Neo4j 中的数据中的另一个库需要您将数据导出到 Neo4j 中,对其进行处理,并可能再次导入结果。使用 GDS 库可以简化流程,因为它允许我们直接在 Neo4j 中运行优化算法。
在 Neo4j 中使用最短路径算法
为了测试 GDS 库中是否实现了最短路径算法,我们将使用自本章开始以来一直使用的相同图。所以让我们首先在 Neo4j 中创建我们的测试图:
CREATE (A:Node {name: "A"})
CREATE (B:Node {name: "B"})
CREATE (C:Node {name: "C"})
CREATE (D:Node {name: "D"})
CREATE (E:Node {name: "E"})
CREATE (A)-[:LINKED_TO {weight: 10}]->(B)
CREATE (A)-[:LINKED_TO {weight: 33}]->(C)
CREATE (A)-[:LINKED_TO {weight: 35}]->(D)
CREATE (B)-[:LINKED_TO {weight: 20}]->(C)
CREATE (C)-[:LINKED_TO {weight: 28}]->(D)
CREATE (C)-[:LINKED_TO {weight: 6 }]->(E)
CREATE (D)-[:LINKED_TO {weight: 40}]->(E)Neo4j 中的结果图如下图所示:
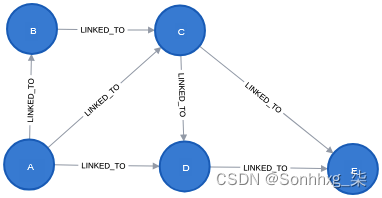
找到两个节点之间的最短路径的过程如下:
gds.alpha.shortestPath.stream(
graphName::STRING,
{
startNode::NODE,
endNode::NODE,
relationshipWeightProperty::STRING
)
(nodeId::INTEGER, cost::FLOAT)配置参数如下:
- 起始节点
- 结束节点
- 包含要用作权重的关系属性的字符串
它返回包含两个元素的最短路径中的节点列表:
- Neo4j 内部节点 ID
- 到该节点的遍历成本
让我们在测试图上使用它来找到 和 之间的最短A路径E。但在我们这样做之前,我们需要定义投影图。在我们的例子中,我们将使用带有标签的节点和带有 Node 标签的关系,LINKED_TO所以创建这个投影图的过程调用如下:
CALL gds.graph.create("graph", "Node", "LINKED_TO")然后我们可以使用这样的最短路径过程:
MATCH (A:Node {name: "A"})
MATCH (E:Node {name: "E"})
CALL gds.alpha.shortestPath.stream("graph", {startNode: A, endNode: E})
YIELD nodeId, cost
RETURN nodeId, cost此查询的结果如下表所示:
╒════════╤══════╕
│"nodeId"│"cost"│
╞════════╪══════╡
│45 │0.0 │
├────────┼──────┤
│48 │1.0 │
├────────┼──────┤
│49 │2.0 │
└────────┴──────┘该nodeId列包含 Neo4j 提供给节点以供内部使用的 ID。您获得的值可能与我的不同,但最重要的是,它们很难解释,因为我们不知道它们对应于哪些节点。幸运的是,GDS 插件包含一个帮助函数来从其 ID 获取节点:gds.util.asNode。因此,让我们更新我们的查询以返回更有意义的内容:
MATCH (A:Node {name: "A"})
MATCH (E:Node {name: "E"})
CALL gds.alpha.shortestPath.stream("graph", {startNode: A, endNode: E})
YIELD nodeId, cost
RETURN gds.util.asNode(nodeId).name as name, cost此查询产生以下输出:
╒══════╤══════╕
│"name"│"cost"│
╞══════╪══════╡
│"A" │0.0 │
├──────┼──────┤
│"D" │1.0 │
├──────┼──────┤
│"E" │2.0 │
└──────┴──────┘现在节点名称是可以理解的。但是,此输出还有另一个问题:它与我们在上一节中找到的不匹配。这是因为该shortestPath过程的默认行为是计算从一个节点到另一个节点的跳数,而不考虑与边相关的任何权重。这相当于将所有边的权重设置为 1。就跳数而言,这个结果是正确的——从A到的可能最短路径E是通过节点 中转D。
要考虑边权重或节点之间的距离,我们必须使用 relationshipWeightProperty配置参数:
MATCH (A:Node {name: "A"})
MATCH (E:Node {name: "E"})
CALL gds.alpha.shortestPath.stream("graph", {
startNode: A,
endNode: E,
relationshipWeightProperty: "weight"
}
)
YIELD nodeId, cost
RETURN gds.util.asNode(nodeId).name as name, cost如果您尝试运行此过程,您将收到以下错误消息:
Failed to invoke procedure `gds.alpha.shortestPath.stream`: Caused by: java.lang.IllegalArgumentException: Relationship weight property `weight` not found in graph with relationship properties: []实际上,我们的投影图graph不包含任何关系属性。您可以使用以下gds.graph.list过程进行检查:
CALL gds.graph.list("graph")
YIELD relationshipProjection
RETURN *这给出了以下结果:
{
"LINKED_TO": {
"aggregation": "DEFAULT",
"projection": "NATURAL",
"type": "LINKED_TO",
"properties": {
}
}
}您可以识别空属性列表。
为了解决这个问题,让我们创建另一个投影图,这次包括weight属性:
CALL gds.graph.create("graph_weighted", "Node", "LINKED_TO", {
relationshipProperties: [{weight: 'weight' }]
}
)现在调用的列表过程graph_weighted告诉我们,我们有一个weight与关系类型相关联的属性LINKED_TO:
{
"LINKED_TO": {
"aggregation": "DEFAULT",
"projection": "NATURAL",
"type": "LINKED_TO",
"properties": {
"weight": {
"property": "weight",
"defaultValue": NaN,
"aggregation": "DEFAULT"
}
}
}
}我们现在可以在这个新的投影图上运行最短路径过程graph_weighted:
MATCH (A:Node {name: "A"})
MATCH (E:Node {name: "E"})
CALL gds.alpha.shortestPath.stream("graph_weighted", {
startNode: A,
endNode: E,
relationshipWeightProperty: "weight"
}
)
YIELD nodeId, cost
RETURN gds.util.asNode(nodeId).name as name, cost这一次,我们得到了我们预期的结果:
╒════╤══════╕
│"id"│"cost"│
╞════╪══════╡
│"A" │0.0 │
├────┼──────┤
│"B" │10.0 │
├────┼──────┤
│"C" │30.0 │
├────┼──────┤
│"E" │36.0 │
└────┴──────┘如果您检查此结果的图形可视化,您会发现四个节点 、、A和,以及它们之间的所有现有关系,而没有过滤属于最短路径的关系。这意味着我们失去了需要访问节点的顺序。这是由于 Neo4j 浏览器中的配置默认选项。要禁用它,您需要转到 Neo4j Desktop 中的设置视图并禁用名为Connect result nodes的选项。在禁用该选项的情况下重新运行上一个查询将仅显示节点。我们现在要稍微调整这个查询,以便可视化真实路径。BCE
路径可视化
为了可视化我们的路径,我们将首先将结果写入图中。这不是强制性的,但会稍微简化以下查询。
gds.alpha.shortestPath.stream我们将调用该gds.alpha.shortestPath.write过程,而不是使用。参数类似,但返回值完全不同:
MATCH (A:Node {name: "A"})
MATCH (E:Node {name: "E"})
CALL gds.alpha.shortestPath.write("graph_weighted", {
startNode: A,
endNode: E,
relationshipWeightProperty: "weight"
}
) YIELD totalCost
RETURN totalCost这会将最短路径算法的结果写入sssp属于最短路径的节点上的属性。
如果我们想检索该路径,包括关系,我们必须找到路径中两个连续节点之间的关系并将其与节点一起返回。这正是以下查询所做的:
MATCH (n:Node)
WHERE n.sssp IS NOT NULL
WITH n
ORDER BY n.sssp
WITH collect(n) as path
UNWIND range(0, size(path)-1) AS index
WITH path[index] AS currentNode, path[index+1] AS nextNode
MATCH (currentNode)-[r:LINKED_TO]-(nextNode)
RETURN currentNode, r, nextNode此 Cypher 查询执行以下操作:
- sssp通过仅保留具有该属性的节点并对它们进行排序来选择属于最短路径的节点。
- 将所有这些节点分组到一个由语句调用的列表path中collect(如果您需要一些提醒,请参阅第 2 章,Cypher 查询语言)。
- 迭代此列表的索引,从 0 到 n-1,其中 n 是 中的节点数path。
- 然后我们可以访问一个节点 ( path[index]) 及其在路径 ( path[index+1]) 中的后续节点。
- 最后,我们可以找到LINDED_TO这两个节点之间的类型关系,并将其作为最终结果的一部分返回。
此查询生成以下图表:

了解关系方向
到目前为止,我们对投影关系的方向使用了默认配置。默认情况下,它与 Neo4j 图相同。
下图说明了传出关系和传入关系之间的区别。就节点A而言,与B的关系是传出的,即从A开始,到B结束,而与C的关系是传入的,即A是结束节点:
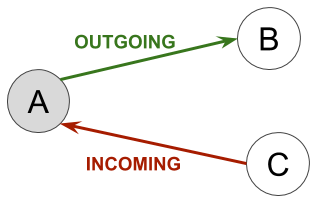
在 GDS 中,您始终可以选择是仅使用传出或传入关系,还是使用双向关系。最后一种情况允许您将图形视为无向的,而所有 Neo4j 关系都必须是有向的。
为了说明这个概念,让我们在测试图中添加一条新边:
MATCH (A:Node {name: "A"})
MATCH (C:Node {name: "C"})
MATCH (E:Node {name: "E"})
CREATE (C)-[:LINKED_TO {weight: 20}]->(A)
CREATE (E)-[:LINKED_TO {weight: 5}]->(C)我们的图表现在看起来像这样:
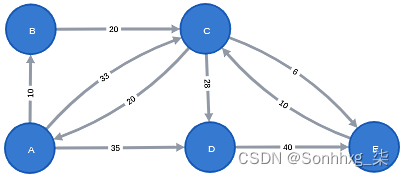
现在让我们创建一个新的投影图,它将使用相反方向的关系:
CALL gds.graph.create("graph_weighted_reverse", "Node", {
LINKED_TO: {
type: 'LINKED_TO',
projection: 'REVERSE',
properties: "weight"
}
}
)请注意,我们还通过将关系属性直接添加到投影关系定义中来简化图形创建查询。
我们现在可以在这个新创建的上运行相同的最短路径算法graph_weighted_reverse:
MATCH (A:Node {name: "A"})
MATCH (E:Node {name: "E"})
CALL gds.alpha.shortestPath.stream("graph_weighted_reverse", {
startNode: A,
endNode: E,
relationshipWeightProperty: "weight"
}
)
YIELD nodeId, cost
RETURN gds.util.asNode(nodeId).name as name, cost结果现在不同了:
╒══════╤══════╕
│"name"│"cost"│
╞══════╪══════╡
│"A" │0.0 │
├──────┼──────┤
│"C" │20.0 │
├──────┼──────┤
│"E" │30.0 │
└──────┴──────┘实际上,考虑到反向关系,最短路径现在直接通过C。
最后但同样重要的是,还可以在投影图中包含两个方向的关系:
CALL gds.graph.create("graph_weighted_undirected", "Node", {
LINKED_TO: {
type: 'LINKED_TO',
projection: 'UNDIRECTED',
properties: "weight"
}
}
)A投影图之间和E上的最短路径graph_weighted_undirected如下:
╒══════╤══════╕
│"name"│"cost"│
╞══════╪══════╡
│"A" │0.0 │
├──────┼──────┤
│"C" │20.0 │
├──────┼──────┤
│"E" │26.0 │
└──────┴──────┘两种情况下选择的路径如下图所示: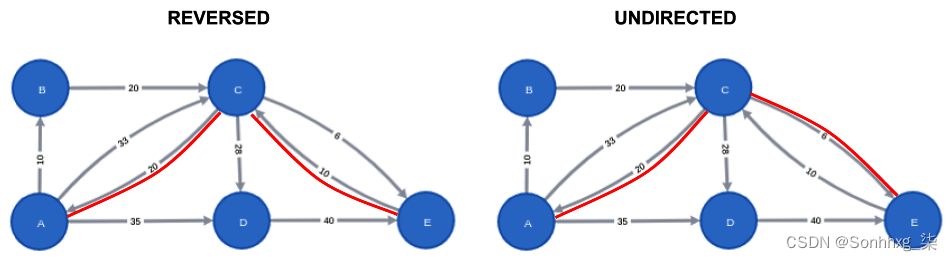
在相反的情况下,算法只能选择反向的关系,这意味着它的迭代在起始节点处结束。在无向场景中,它可以选择传出或传入关系。然后它将选择最小化总成本的路径。
我们对 Dijkstra 算法的讨论到此结束。在审查了算法的功能之后,我们已经能够通过 GDS 插件直接在存储在 Neo4j 数据库中的图形上使用它。尽管这可能是最著名的寻路算法,但 Dijkstra 的算法并不总是表现最好的。在下一节中,我们将讨论 A* 算法,这是另一种受 Dijkstra 算法启发的寻路算法。
使用 A* 算法及其启发式查找最短路径
A* 算法(发音为A-star )由 P. Hart、N. Nilsson 和 B. Raphael 于 1968 年开发,是 Dijkstra 算法的扩展。由于启发式算法,它试图通过猜测遍历方向来优化搜索。由于这种方法,已知它比 Dijkstra 的算法更快,尤其是对于大型图。
算法原理
在 Dijkstra 算法中,探索了所有可能的路径。这可能非常耗时,尤其是在大型图表上。A* 算法试图克服这个问题,其想法是它可以猜测要遵循的路径以及哪些路径扩展不太可能是最短路径。这是通过在每次迭代中修改选择下一个起始节点的标准来实现的。A* 算法不是仅使用从起点到当前节点的路径成本,而是添加了另一个组件:从当前节点到终点节点的估计成本。可以表示如下:
虽然costSoFar(currentNode)与 Dijkstra 算法中计算的结果相同,但它estimatedCost(currentNode, endNode)是对从当前节点到结束节点的剩余成本的猜测。猜测函数,通常记为h,是一个启发式函数。
定义 A* 的启发式
启发式函数的选择很重要。如果我们h(n) = 0为所有节点设置,A* 算法等效于 Dijkstra 算法,我们不会看到性能提升。如果h(n)距离真实距离太远,算法就会冒着找不到真实最短路径的风险。启发式的选择是速度和准确性之间的平衡问题。
在 GDS 插件中,实施的启发式算法使用hasrsine方程。这是一个计算地球表面两点之间距离的公式,给定它们的纬度和经度。它对应于大圆距离,如下图所示: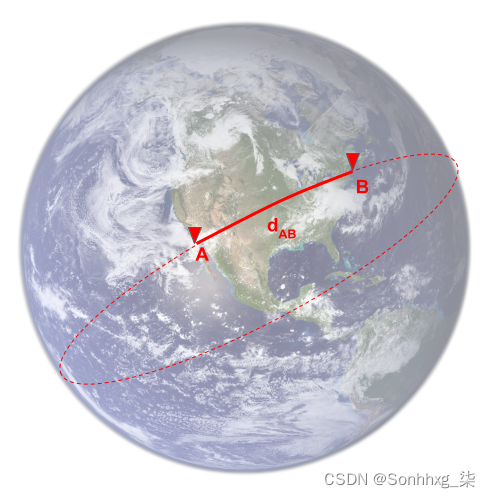
猜测函数忽略了网络的确切形状,但可以说,从A到B,你更有可能通过开始向右移动而不是向左移动来找到最短路径,所以你会到达目标节点的迭代次数更少。
使用 hasrsine 公式意味着只有在投影图中的节点具有空间属性(纬度和经度)的情况下,才能使用 Neo4j 的 A* 算法。
在 Neo4j GDS 插件中使用 A*
A* 算法可通过该gds.alpha.shortestPath.astar过程访问。签名遵循与其他算法相同的模式:第一个参数是算法将使用的投影图的名称,而第二个参数是每个算法特定的映射。在 A* 算法配置中,我们将找到相同的startNode, endNode,并且relationshipWeightProperty我们已经用于该shortestPath过程。最重要的是,添加了两个新属性来指定保存纬度和经度的节点属性的名称:propertyKeyLat和propertyKeyLon。下面是在投影图上调用 A* 算法的示例:
MATCH (A:Node {name: "A"})
MATCH (B:Node {name: "B"})
CALL gds.alpha.shortestPath.astar.stream("graph", {
startNode: A,
endNode: B,
relationshipWeightProperty: "weight",
propertyKeyLat: "latitude",
propertyKeyLon: "longitude",
}
) YIELD nodeId, cost
RETURN gds.asNode(nodeId).name, cost我们将在下一章(第 5 章,空间数据)中使用这个算法,在那里我们将能够构建一个真正的路由引擎。
但在此之前,我们将了解与最短路径查找相关的其他算法,例如全对最短路径或生成树算法。
在 GDS 插件中发现其他与路径相关的算法
能够找到两个节点之间的最短路径很有用,但并不总是足够的。幸运的是,可以扩展最短路径算法以提取更多关于图中路径的信息。以下小节详细介绍了在 GDS 插件中实现的那些算法的部分。
K-最短路径
Dijkstra 算法和 A* 算法只返回两个节点之间可能的最短路径。如果您对第二最短路径感兴趣,则必须选择 k 最短路径或Yen 算法。它在 GDS 插件中的使用与我们之前研究的算法非常相似,只是我们必须指定要返回的路径数。在以下示例中,我们指定k=2:
MATCH (A:Node {name: "A"})
MATCH (E:Node {name: "E"})
CALL gds.alpha.kShortestPaths.stream("graph_weighted", {
startNode: A,
endNode: E,
k:2,
relationshipWeightProperty: "weight"}
)
YIELD index, sourceNodeId, targetNodeId, nodeIds
RETURN index,
gds.util.asNode(sourceNodeId).name as source,
gds.util.asNode(targetNodeId).name as target,
gds.util.asNodes(nodeIds) as path 结果如下表所示。第一条最短路径是我们已经知道的:A, B, C, E。第二个最短路径是A, C, E:
╒═══════╤════════╤════════╤═══════════════════════════════════════════════════════╕
│"index"│"source"│"target"│"path" │
╞═══════╪════════╪════════╪═══════════════════════════════════════════════════════╡
│0 │"A" │"E" │[{"name":"A"},{"name":"B"},{"name":"C"},{"name":"E"}] │
├───────┼────────┼────────┼───────────────────────────────────────────────────────┤
│1 │"A" │"E" │[{"name":"A"},{"name":"C"},{"name":"E"}] │
└───────┴────────┴────────┴───────────────────────────────────────────────────────┘在尝试定义替代路线时,此算法非常有用。
单源最短路径 (SSSP)
SSSP 算法的目的是找到给定节点与图中所有其他节点之间的最短路径。它也基于 Dijkstra 算法,但通过将节点打包到桶中并单独处理每个桶来实现并行执行。并行度由存储桶大小控制,存储桶大小本身由delta参数决定。设置 时delta=1,SSSP 完全等同于使用 Dijkstra 算法,即不使用并行性。delta 值太高(大于所有边权重的总和)会将所有节点放在同一个桶中,从而抵消并行性的影响。
GDS 库中的过程称为deltaStepping. 它的签名符合预期:
CALL gds.shortestPath.deltaStepping.stream(graphName::STRING, configuration::MAP)但是,它的配置略有不同:
- startNode: 计算所有最短路径的节点
- relationshipWeightProperty:通常的关系属性承载重量
- delta: 控制并行度的 delta 参数
使用我们的简单图表,我们可以使用这个过程来delta=1使用这个查询:
MATCH (A:Node {name: "A"})
CALL gds.alpha.shortestPath.deltaStepping.stream("graph_weighted", {
startNode: A,
relationshipWeightProperty: "weight",
delta: 1
}
)
YIELD nodeId, distance
RETURN gds.util.asNode(nodeId).name, distance返回值如下:
╒════════════════════════════╤══════════╕
│"gds.util.asNode(nodeId).name"│"distance"│
╞════════════════════════════╪══════════╡
│"A" │0.0 │
├────────────────────────────┼──────────┤
│"B" │10.0 │
├────────────────────────────┼──────────┤
│"C" │30.0 │
├────────────────────────────┼──────────┤
│"D" │35.0 │
├────────────────────────────┼──────────┤
│"E" │36.0 │
└────────────────────────────┴──────────┘第一列包含图中的每个节点,第二列是从startNode, A, 到其他节点的距离。A在这里我们再次遇到了36的最短距离E。我们还发现了之前运行 Dijkstra 算法时发现的结果:和之间的最短距离A是B10,和之间A的最短距离是C30。除此之外,我们还有一个新结果:到 的最短距离A为D35。
All-pairs shortest path
All-pairs shortest path算法更进一步:它返回投影图中每对节点之间的最短路径。它相当于为每个节点调用 SSSP,但进行了性能优化以使其更快。
该算法的 GDS 实现过程如下所示:
CALL gds.alpha.allShortestPaths.stream(graphName::STRING, configuration::MAP)
YIELD sourceNodeId, targetNodeId, distance与往常一样,配置参数包括relationshipWeightProperty投影图中要用作权重的关系属性。
有两个额外的参数来设置并发线程的数量:concurrency和readConcurrency.
我们可以在我们的小测试图上使用它,如下所示:
CALL gds.alpha.allShortestPaths.stream("graph_weighted", {
relationshipWeightProperty: "weight"
})
YIELD sourceNodeId, targetNodeId, distance
RETURN gds.util.asNode(sourceNodeId).name as start,
gds.util.asNode(targetNodeId).name as end,
distance结果是以下矩阵:
╒═══════╤═════╤══════════╕
│"start"│"end"│"distance"│
╞═══════╪═════╪══════════╡
│"B" │"B" │0.0 │
├───────┼─────┼──────────┤
│"B" │"C" │20.0 │
├───────┼─────┼──────────┤
│"B" │"D" │48.0 │
├───────┼─────┼──────────┤
│"B" │"E" │26.0 │
├───────┼─────┼──────────┤
│"A" │"A" │0.0 │
├───────┼─────┼──────────┤
│"A" │"B" │10.0 │
├───────┼─────┼──────────┤
│"A" │"C" │30.0 │
├───────┼─────┼──────────┤
│"A" │"D" │35.0 │
├───────┼─────┼──────────┤
│"A" │"E" │36.0 │
├───────┼─────┼──────────┤
│"C" │"C" │0.0 │
├───────┼─────┼──────────┤
│"C" │"D" │28.0 │
├───────┼─────┼──────────┤
│"C" │"E" │6.0 │
├───────┼─────┼──────────┤
│"D" │"D" │0.0 │
├───────┼─────┼──────────┤
│"D" │"E" │40.0 │
├───────┼─────┼──────────┤
│"E" │"E" │0.0 │
└───────┴─────┴──────────┘您现在可以从图表中提取以下与路径相关的信息:
- 两个节点之间的一条或多条最短路径
- 图中一个节点与所有其他节点之间的最短路径
- 所有节点对之间的最短路径。
在下一节中,我们将讨论图优化问题。旅行商问题是最著名的图优化问题。
使用图表优化流程
优化问题的目标是在大量候选者中找到最优解。您最喜欢的汽水罐的形状源自一个优化问题,试图在给定体积(33 cl)下尽量减少使用的材料(表面)量。在这种情况下,曲面,即要最小化的量,也称为目标函数。
优化问题通常伴随着对变量的一些限制。从数学上讲,长度必须为正的事实已经是一个约束。但是约束可以用许多不同的形式来表达。
优化问题的更简单形式是所谓的线性优化,其中目标函数和约束都是线性的。
图优化问题也是数学优化问题的一部分。其中最著名的是旅行商问题(TSP)。我们将在下一节中更多地讨论这个特定问题。
旅行商问题
TSP 是计算机科学中的一个著名问题。给定一个城市列表和每个城市之间的最短距离,目标是找到访问所有城市一次且仅一次并返回起点的最短路径。下面的地图说明了旅行商问题的解决方案,访问了德国的一些城市:
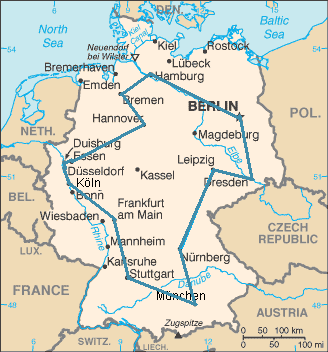
所以我们有一个优化问题如下:
- 目标函数:路径的成本。这个成本可以是总距离,但如果司机只按小时付费,那么使用总行程时间作为最小化目标可能更有用。
- 约束:
- 每个城市必须访问一次,而且只能访问一次。
- 路径必须在同一个城市开始和结束。
尽管公式很简单,但这是一个 NP-hard 问题。在所有情况下达到精确解决方案的唯一方法是蛮力方法,您可以计算每对节点之间的最短路径(allPairsShortestPath算法的应用)并检查所有可能的排列。这种方法的时间复杂度是O(number of nodes!)。你可以想象,只有几个节点,这种解决方案对于普通计算机来说是不可能的。假设每个组合需要 1 毫秒的处理时间,那么具有 15 个节点的配置将需要 15 毫秒,这意味着测试所有可能的组合需要超过 41 年。有了 20 个节点,这个计算时间增加到超过 7700 万年。
幸运的是,存在一些算法来找到不能保证 100% 准确但足够接近的解决方案。提供此类解决方案的详尽列表超出了本书的范围,但我们可以引用两个最常见的解决方案,它们都基于科学和自然的类比:
- 蚁群优化( ACO ):该算法基于观察蚂蚁在蚁群中如何使用信息素(气味分子)相互通信以实现完美同步。在该算法中,许多探索者蚂蚁(代理)被发送到图中并基于一些局部优化沿着其边缘移动。
- 基因算法( GA ):这些算法基于与遗传学的类比,以及基因如何通过突变代代相传,以选择更强大的个体。
TSP 可以扩展到更复杂的用例。例如,如果一家快递公司有不止一辆可用的车辆,我们可以扩展 TSP 问题以确定对不止一位推销员的最佳行动方案。这被称为多重旅行商问题( MTSP )。还可以添加更多约束,例如:
- 容量限制,每辆车都有容量限制,最多只能运载一定数量的货物。
- 时间窗口限制:在某些情况下,包裹只能在某个时间窗口内交付。
这些 TSP 算法(尚未)在 GDS 插件中实现。但是,我们可以使用生成树算法找到最优解的上限。
生成树
生成树是从原始图构建的,这样:
- 生成树中的节点与原始图中的节点相同。
- 在原始图中选择生成树边,以使生成树中的所有节点都连接起来,而不会创建循环。
下图说明了我们在本章中研究过的图的一些生成树: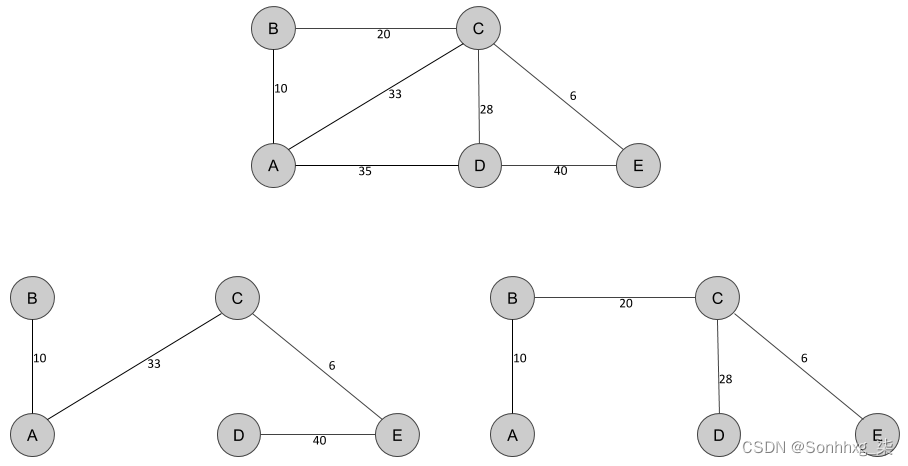
在所有可能的生成树中,最小生成树是所有边的权重和最小的生成树。在上图中,左下生成树的权重总和为 89(10+33+6+40),而右下生成树的权重总和为 64(10+20+28 +6)。因此,右下生成树更可能是最小生成树。为了验证这一点,在下一节中,我们将讨论 GDS 插件中实现的用于查找生成树的算法,即 Prim 算法。
Prim 算法
这就是 Prim 算法在我们简单的测试图上运行的方式:
- 它选择一个起始节点——下图中的节点A。
- 迭代 1:它检查连接到该节点的所有边,并选择权重最低的边。选择顶点B ,并将A和B之间的边添加到树中。
- 从B开始,它访问C。在C和D中是已经访问过的节点。权重最低的是C,因此选择了C并将B和C之间的边添加到树中。
- 从C开始,可以到A、D和E。A已经被访问过,新的边(C -> A)会比已经存在的边增加一个更高的权重,所以这个边被跳过。但是,您可以看到到达D ( C -> D ) 的新边的权重低于先前选择的边 ( A -> D ),这意味着从树中删除了前一条边并添加了新边。
- 最后一步包括检查最后一个节点E。在这里,添加D和E之间的边会使总权重增加 40 而不是 6(C和E之间的边的权重),因此最后一条边被跳过。
下图总结了这四次迭代,包括边缘创建(绿线)、边缘未考虑(绿色虚线)和边缘移除(红色虚线):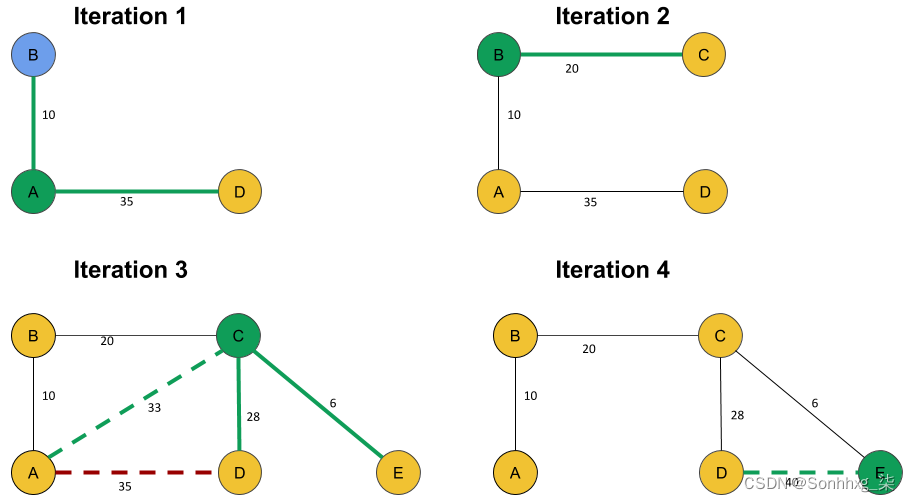
我们图的最小生成树由以下边组成:
A-B (weight 10)
B-C (weight 20)
C-D (weight 28)
C-E (weight 6)您可以检查所有节点是否连接(图中每对节点之间有一条路径),总权重为64。
让我们尝试从 Neo4j 中检索这些信息。
在 Neo4j 图中找到最小生成树
在 GDS 插件中查找最小生成树的过程如下:
MATCH (A:Node {name: "A"})
CALL gds.alpha.spanningTree.minimum.write("graph_weighted", {
startNodeId: id(A),
relationshipWeightProperty: 'weight',
writeProperty: 'MINST',
weightWriteProperty: 'writeCost'
})
YIELD createMillis, computeMillis, writeMillis, effectiveNodeCount
RETURN *这实际上将为最小生成树中的每条边创建新的关系。要检索这些边,您可以使用以下命令:
MATCH (n)-[r:MST]-(m)
RETURN n, r, m此查询产生以下输出,与我们之前通过运行 Prim 算法获得的结果一致:
请注意,您还可以找到最大生成树和 k 生成树来找到仅使用 k 个节点的生成树。
概括
这一章很长,因为它是我们对 GDS 插件的介绍。了解如何定义投影图以及要包含在其中的不同实体非常重要。我们将在接下来的章节中看到更多示例,因为我们将在本书的所有剩余章节中使用这个库。
下表总结了我们在本章中研究的不同算法,并记住了一些重要的特征:
| 算法 | 描述 | Stream/Write | Negative weights |
| shortestPath | 使用 Dijkstra 算法的两个节点之间的最短路径 | 两个都 | 不 |
| shortestPath.astar | 使用 A* 算法和大圆启发式算法的两个节点之间的最短路径(需要具有纬度和经度属性的节点) | Stream | 不 |
| kShortestPath | 使用 Yen 算法的两个节点之间的 k 最短路径 | 两个都 | 是的 |
| shortestPath.deltaStepping | 单源最短路径:图中一个节点与所有其他节点之间的最短路径 | 两个都 | 不 |
| allShortestPaths | 图中每对节点之间的最短路径 | Stream | 不 |
| spanningTree.* | 图中的最小、最大或 k 生成树 | Write | 是的 |
正如您将在接下来的章节中发现的那样,最短路径也可用于推断图上的其他指标,例如节点重要性(第 5 章,节点重要性)。但在进入这些算法之前,正如我们在本章中讨论了很多关于路由和地理数据的那样,下一章将专门介绍 Neo4j 中的地理数据管理,使用内置数据类型和另一个 Neo4j 插件:neo4j-spatial.
问题
为了测试您的理解,请尝试回答以下问题。本书末尾的评估部分提供了答案:
1.GDS 插件和投影图:
- 为什么 GDS 插件使用投影图?
- 这些投影图存储在哪里?
- 命名投影图和匿名投影图有什么区别?
- 创建一个投影图,其中包含:
- 节点:标签Node
- 关系:类型REL1和REL2
- 创建一个投影图:
- 节点:标签Node1和Node2
- 关系:类型REL1和属性prop1以及prop2
- 您如何使用 GDS 插件中的图形算法的结果?
2.寻找路径:
- 哪些算法基于 Dijkstra 算法?
- 这些算法的边权重的重要限制是什么?
- 使用 A* 算法需要哪些信息?
进一步阅读
- 图算法在视频游戏中的应用:游戏中 AI 的图算法 [视频], D. Jallov,Packt Publishing
- https://github.com/stellasia/neoplus提供了具有自定义功能和过程的示例项目。它包括使用 Neo4j Java API 的 Dijkstra 算法的实现。
- A* 和启发式:http ://theory.stanford.edu/~amitp/GameProgramming/Heuristics.html
- 路由优化求解器,包括旅行商问题,由 Google 提供:https ://developers.google.com/optimization/routin
相关文章
- 大数据必学Java基础(八十八):通过案例和概念体会反射的好处
- Nature子刊:大脑时间工具箱-将电生理数据与脑动力学结合
- Mock数据 – Java最好用的工具JMockData
- mybatis 处理数组类型及使用Json格式保存数据 JsonTypeHandler and ArrayTypeHandler详解编程语言
- 【MySQL查询获取日期数据】(mysql取date)
- 数据Oracle客户端快速导出数据指南(oracle客户端导出)
- Redis Persistence: Ensure Secure Data Storage and Retrieval(redis保存数据)
- Oracle数据库中的AND查询(oracle and查询)
- MySQL中in用法详解,让你轻松掌握数据查询技巧(mysql中in用法)
- 深入探究Mysql中IN与AND逻辑运算的应用(mysql中in与and)
- MySQL中如何正确使用AND运算符(mysql中and怎么用)
- MySQL轻松实现一秒插入万条数据(MySQL一秒插入条)
- 清空历史Redis中的零点清零(redis零点清零数据)
- c#将Excel数据导入到数据库的实现代码
- JSON数据转换成Java对象的方法

