Python小白的数学建模课-B3. 新冠疫情 SIS模型

传染病的数学模型是数学建模中的典型问题，常见的传染病模型有 SI、SIR、SIRS、SEIR 模型。

SIS 模型型将人群分为 S 类和 I 类，考虑患病者可以治愈而变成易感者，但不考虑免疫期。

本文详细给出了 SIS 模型的建模、例程、运行结果和模型分析，让小白都能懂。

『Python小白的数学建模课 @ Youcans』带你从数模小白成为国赛达人。

Python小白的数学建模课-A3.12个新冠疫情数模竞赛赛题及短评
Python小白的数学建模课-B2. 新冠疫情 SI模型
Python小白的数学建模课-B3. 新冠疫情 SIS模型
Python小白的数学建模课-B4. 新冠疫情 SIR模型
Python小白的数学建模课-B5. 新冠疫情 SEIR模型
Python小白的数学建模课-B6. 新冠疫情 SEIR改进模型

---

1. 疫情传播 SIS 模型

传染病动力学是对传染病进行定量研究的重要方法。它依据种群繁衍迁移的特性、传染病在种群内产生及传播的机制、医疗与防控条件等外部因素，建立可以描述传染病动力学行为的数学模型，通过对模型进行定性、定量分析和数值计算，模拟传染病的传播过程，预测传染病的发展趋势，研究防控策略的作用。

1.1 SI 模型

SI 模型把人群分为易感者（S类）和患病者（I类）两类，易感者（S类）与患病者（I类）有效接触即被感染，变为患病者，无潜伏期、无治愈情况、无免疫力。

SI 模型适用于只有易感者和患病者两类人群，且无法治愈的疾病。

按照 SI 模型，最终所有人都会被传染而变成病人，这是因为模型中没有考虑病人可以治愈。因此只能是健康人患病，而患病者不能恢复健康（甚至也不会死亡，而是不断传播疫情），所以终将全部被传染。

1.2 SIS 模型

SIS 模型将人群分为 S 类和 I 类，考虑患病者（I 类）可以治愈而变成易感者（S 类），但不考虑免疫期，因此患病者（I 类）治愈变成易感者以后还可以被感染而变成患病者。

SIS 模型适用于只有易感者和患病者两类人群，可以治愈，但会反复发作的疾病，例如脑炎、细菌性痢疾等治愈后也不具有免疫力的传染病。

SIS 模型假设：

1. 考察地区的总人数 N 不变，即不考虑生死或人口流动；
2. 人群分为易感者（S类）和患病者（I类）两类；
3. 易感者（S类）与患病者（I类）有效接触即被感染，变为患病者；患病者（I类）可被治愈而变为易感者，无潜伏期、无免疫力；
4. 每个患病者每天有效接触的易感者的平均人数（日接触数）是 $\lambda$，称为日接触率；
5. 每天被治愈的患病者人数占患病者总数的比例为 $\mu$ ，即日治愈率；
6. 将第 t 天时 S类、I 类人群的占比记为 $s(t)$、$i(t)$，数量为 $S(t)$、$I(t)$；初始日期 $t=0$ 时， S类、I 类人群占比的初值为 $s_0$、$i_0$。

需要说明的是，不考虑生死或人口流动，通常是由于考虑一个封闭环境而且假定疫情随时间的变化比生死、迁移随时间的变化显著得多, 因此后者可以忽略不计。

SIS 模型的微分方程：

由
$$N\frac{di}{dt}=N\lambda si-N\mu i$$
得：
$$\frac{di}{dt}=\lambda i(1-i)-\mu i，i(0)=i_0$$
由日治愈率 $\mu$ 可知平均治愈天数为 $1/\mu$，也称平均传染期。定义 $\sigma =\lambda /\mu$，其含义是每个病人在传染期内所传染的平均人数，称为传染期接触数。例如，平均传染期 $1/\mu =5$，日接触率 $\lambda =2$（每天传染 2人），则传染期接触数 $\sigma =10$。

SIS 模型的解析解为：
$$\{\begin{array}{l}\begin{array}{rlr}& i(t)=\frac{i_0}{1+\lambda t{i}_0}& ,\lambda =\mu \\ & i(t)=[\frac{\lambda }{\lambda -\mu }+(\frac{1}{i_0}-\frac{\lambda }{\lambda -\mu })\ast e^{-(\lambda -\mu )t}{]}^{-1}& ,\lambda \ne \mu \end{array}\end{array}$$

注意：网上有些博文中解析解的公式误写成 $exp((\lambda -\mu )t)$ ，漏掉了一个负号。

---

2. SIS 模型的 Python 编程

2.1 Scipy 工具包求解 SIS 模型

SIS 模型是常微分方程初值问题，可以使用 Scipy 工具包的 scipy.integrate.odeint() 函数求数值解。

scipy.integrate.odeint(func, y0, t, args=())

**scipy.integrate.odeint() **是求解微分方程的具体方法，通过数值积分来求解常微分方程组。

odeint() 的主要参数：

• func: callable(y, t, …) 　　导数函数 $f(y,t)$ ，即 y 在 t 处的导数，以函数的形式表示
• y0: array：　　初始条件 $y_0$，对于常微分方程组 $y_0$ 则为数组向量
• t: array：　　求解函数值对应的时间点的序列。序列的第一个元素是与初始条件 $y_0$ 对应的初始时间 $t_0$；时间序列必须是单调递增或单调递减的，允许重复值。
• args: 向导数函数 func 传递参数。当导数函数 $f(y,t,p1,p2,..)$ 包括可变参数 p1,p2… 时，通过 args =(p1,p2,…) 可以将参数p1,p2… 传递给导数函数 func。

odeint() 的返回值：

• y: array 　　数组，形状为 (len(t),len(y0)，给出时间序列 t 中每个时刻的 y 值。

odeint() 的编程步骤：

1. 导入 scipy、numpy、matplotlib 包；
2. 定义导数函数 $f(i,t)=\lambda i(1-i)-\mu i$ ；
3. 定义初值 $y_0$ 和 $y$ 的定义区间 $[t_0,t]$；
4. 调用 odeint() 求 $y$ 在定义区间 $[t_0,t]$ 的数值解。

2.2 Python例程：SIS 模型的解析解与数值解

# 1. SIS 模型，常微分方程，解析解与数值解的比较
from scipy.integrate import odeint  # 导入 scipy.integrate 模块
import numpy as np  # 导入 numpy包
import matplotlib.pyplot as plt  # 导入 matplotlib包

def dy_dt(y, t, lamda, mu):  # SIS 模型，导数函数
    dy_dt = lamda*y*(1-y) - mu*y  # di/dt = lamda*i*(1-i)-mu*i
    return dy_dt

# 设置模型参数
number = 1e5  # 总人数
lamda = 1.2  # 日接触率, 患病者每天有效接触的易感者的平均人数
sigma = 2.5  # 传染期接触数
mu = lamda/sigma  # 日治愈率, 每天被治愈的患病者人数占患病者总数的比例
fsig = 1-1/sigma
y0 = i0 = 1e-5  # 患病者比例的初值
tEnd = 50  # 预测日期长度
t = np.arange(0.0,tEnd,1)  # (start,stop,step)
print("lamda={}\tmu={}\tsigma={}\t(1-1/sig)={}".format(lamda,mu,sigma,fsig))

# 解析解
if lamda == mu:
    yAnaly = 1.0/(lamda*t +1.0/i0)
else:
    yAnaly= 1.0/((lamda/(lamda-mu)) + ((1/i0)-(lamda/(lamda-mu))) * np.exp(-(lamda-mu)*t))
# odeint 数值解，求解微分方程初值问题
ySI = odeint(dy_dt, y0, t, args=(lamda,0))  # SI 模型
ySIS = odeint(dy_dt, y0, t, args=(lamda,mu))  # SIS 模型

# 绘图
plt.plot(t, yAnaly, '-ob', label='analytic')
plt.plot(t, ySIS, ':.r', label='ySIS')
plt.plot(t, ySI, '-g', label='ySI')

plt.title("Comparison between analytic and numerical solutions")
plt.axhline(y=fsig,ls="--",c='c')  # 添加水平直线
plt.legend(loc='best')  # youcans
plt.axis([0, 50, -0.1, 1.1])
plt.show()

2.3 SIS 模型解析解与数值解的比较

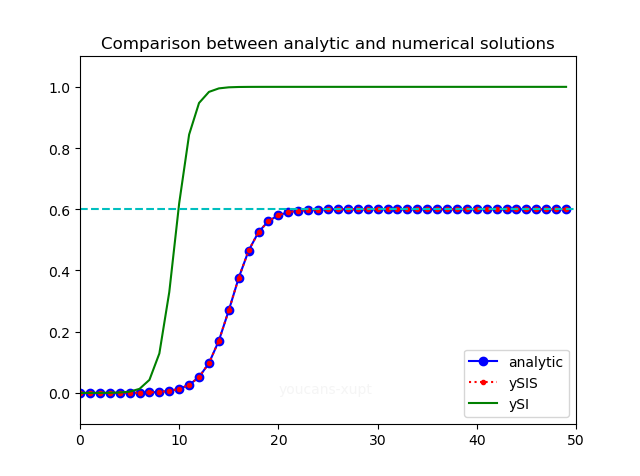
本图为例程 2.2 的运行结果，图中对解析解（蓝色）与使用 odeint() 得到的数值解（红色）进行比较。在该例中，无法观察到解析解与数值解的差异，表明数值解的误差很小。

本图也比较了对相同日接触率和患病者初值下 SI模型与 SIS模型进行了比较。SI 模型更早进入爆发期，最终收敛到 100%；SIS 模型下进入爆发期较晚，患病者的比例最终收敛到某个常数（与模型参数有关）。

考察 SI 模型与 SIS模型的关系，显然 SI 模型是 SIS 模型在 $\mu =0$ 时的特殊情况。

---

3. SIS 模型参数的影响

对于 SIS 模型，需要考虑日接触率 $\lambda$ 与日治愈率 $\mu$ 的关系、患病者比例的初值 $i_0$ 的影响，总人数 N 没有影响。

3.1 日接触率 $\lambda$ 与日治愈率 $\mu$ 关系的影响

直观地考虑，如果每天治愈的人数高于感染的人数，则疫情逐渐好转，否则疫情逐渐严重。因此日接触率 $\lambda$ 与日治愈率 $\mu$ 的关系非常关键，这就是传染期接触数 $\sigma =\lambda /\mu$ 的意义。

（1） $\sigma \le 1$

当 $\sigma <1$ 时，传染期接触数小于 1，日接触率小于日治愈率，患病率单调下降，最终清零，与患病率初值无关。 $\sigma$ 越小，疫情清零速度越快； $\sigma$ 越接近于 1，疫情清零越慢，但最终仍将清零。

分析其实际意义，传染期接触数小于 1，表明在传染期内经过接触而使易感者变成患病者的数量，小于在传染期内治愈的患病者的数量，因此患病者数量、比例都会逐渐降低，所以最终可以清零，称为无病平衡点。

当 $\sigma =1$ 时，不论患病率初值如何，患病率也是单调下降，最终趋近于 0。虽然在数学上患病率只能趋近于 0 而不等于 0，但考虑到总人数 N 是有限的，而患病者和易感者人数需要取整，因此 $\sigma =1$ 时最终也会清零。

（2） $\sigma >1$

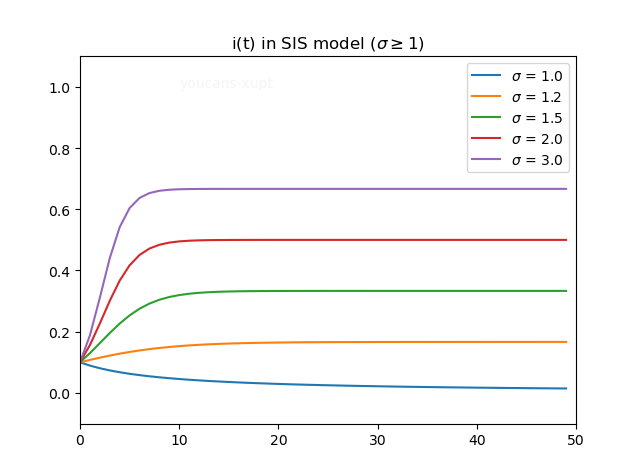
当 $\sigma >1$ 时，传染期接触数大于 1，日接触率大于日治愈率，患病率的升降有两种情况：

当患病率很低时，患病者人数少而易感者人数多，患病率上升；但随着患病率增大，患病者越来越多而易感者越来越少，患病率虽然仍然上升但上升速度趋缓，最终趋于定值。

当患病率很高时，患病者人数多而易感者人数少，患病率下降；但随着患病率减小，患病者越来越少而易感者越来越多，患病率虽然仍然下降但下降速度趋缓，最终也趋于相同的定值。

患病率最终都会收敛到稳态特征值 $i_{\infty }=1-1/\sigma$。当 $i_0>i_{\infty }$ 即患病率初值大于稳态特征值时，疫情曲线单调上升收敛；当 $i_0<i_{\infty }$ 即患病率初值小于稳态特征值时，疫情曲线单调下降收敛；当 $i_0=i_{\infty }$ 时，患病率始终大于稳态特征值，疫情曲线为水平直线。

这表明，当 $\sigma >1$ 时疫情终将稳定但不会清零，而是长期保持一定的患病率，称为地方病平衡点。

当 $\sigma =1$ 时，不论患病率初值如何，患病率都单调下降并最终趋于 0。

3.2 传染期接触数 $\sigma$ 与 $di/dt$ 的关系

患病率的一阶导数 $di/dt$ 的变化曲线，表明不论传染期接触数和初值如何，患病率的变化率都将收敛到 0，因此疫情终将稳定。当 $\sigma <1$ 时， $di/dt$ 始终是负值，单调上升趋近于 0； 当 $\sigma >1$ 时， $di/dt$ 始终是正值，先上升达到峰值后再逐渐减小趋近于 0。

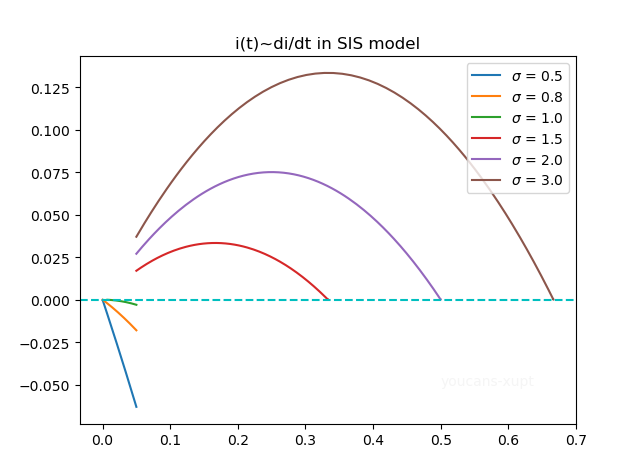
本图为患病率 $i(t)$ 与一阶导数 $di/dt$ 在不同传染期接触数下的关系曲线（相空间图）。当 $\sigma \le 1$ 时，曲线收敛到原点 $(0,0)$，即存在无病平衡点； 当 $\sigma >1$ 时，曲线收敛到 $(1-1/\sigma ,0)$，即存在地方病平衡点。

3.3 Python例程：传染期接触数 $\sigma$ 与 $di/dt$ 的关系

# 4. SIS 模型，模型参数对 di/dt的影响
from scipy.integrate import odeint  # 导入 scipy.integrate 模块
import numpy as np  # 导入 numpy包
import matplotlib.pyplot as plt  # 导入 matplotlib包

def dy_dt(y, t, lamda, mu):  # SIS 模型，导数函数
    dy_dt = lamda*y*(1-y) - mu*y  # di/dt = lamda*i*(1-i)-mu*i
    return dy_dt

# 设置模型参数
number = 1e5  # 总人数
lamda = 1.2  # 日接触率, 患病者每天有效接触的易感者的平均人数
# sigma = np.array((0.1, 0.5, 0.8, 0.95, 1.0))  # 传染期接触数
sigma = np.array((0.5, 0.8, 1.0, 1.5, 2.0, 3.0))  # 传染期接触数
y0 = i0 = 0.05  # 患病者比例的初值
tEnd = 100  # 预测日期长度
t = np.arange(0.0,tEnd,0.1)  # (start,stop,step)

for p in sigma:
    ySIS = odeint(dy_dt, y0, t, args=(lamda,lamda/p))  # SIS 模型
    yDeriv = lamda*ySIS*(1-ySIS) - ySIS*lamda/p
    # plt.plot(t, yDeriv, '-', label=r"$\sigma$ = {}".format(p))
    plt.plot(ySIS, yDeriv, '-', label=r"$\sigma$ = {}".format(p)) #label='di/dt~i'
    print("lamda={}\tmu={}\tsigma={}\t(1-1/sig)={}".format(lamda,lamda/p,p,(1-1/p)))

# 绘图
plt.axhline(y=0,ls="--",c='c')  # 添加水平直线
plt.title("i(t)~di/dt in SIS model") # youcans-xupt
plt.legend(loc='best')
plt.show()

---

4. SIS 模型结果讨论

SIS 模型表明：

1. 若 $\sigma >1$，则 $\underset{t\to \infty }{\lim }i(t)=1-1/\sigma$， 表明患病者始终存在，成为地方病。
2. 若 $\sigma \le 1$，则 $\underset{t\to \infty }{\lim }i(t)=0,(\sigma \le 1)$ ，表明患病者人数不断减少，最终可以清零。
3. SIS 模型说明，对于传染病，需要对患病者进行隔离以减少有效接触，通过减少日接触率 $\lambda$ 来减小接触数 $\sigma$ ，打破传播链，最终控制疫情。

需要指出的是，本文讨论的 SIS模型是把考察地区视为一个疫情均匀分布的整体进行研究。实际上，在考察区域的疫情分布必然是不均衡的，可能在局部区域发生疫情爆发导致该区域患病人数激增，是否会影响 SIS 模型的演化过程和稳定性呢？相关研究表明，扩散速度的不同可能导致种群空间分布的差异，在低风险区域将达到无病平衡点，在高风险区域仍将达到地方病平衡点。

【本节完】

版权声明：

欢迎关注『Python小白的数学建模课 @ Youcans』 原创作品

原创作品，转载必须标注原文链接：https://blog.csdn.net/youcans/article/details/117786272

Copyright 2021 Youcans, XUPT

Crated：2021-06-10

欢迎关注 『Python小白的数学建模课 @ Youcans』 系列，持续更新
Python小白的数学建模课-01.新手必读
Python小白的数学建模课-02.数据导入
Python小白的数学建模课-03.线性规划
Python小白的数学建模课-04.整数规划
Python小白的数学建模课-05.0-1规划
Python小白的数学建模课-06.固定费用问题
Python小白的数学建模课-07.选址问题
Python小白的数学建模课-09.微分方程模型
Python小白的数学建模课-10.微分方程边值问题
Python小白的数学建模课-A1.国赛赛题类型分析
Python小白的数学建模课-A2.2021年数维杯C题探讨
Python小白的数学建模课-A3.12个新冠疫情数模竞赛赛题及短评
Python小白的数学建模课-B2. 新冠疫情 SI模型
Python小白的数学建模课-B3. 新冠疫情 SIS模型
Python小白的数学建模课-B4. 新冠疫情 SIR模型
Python小白的数学建模课-B5. 新冠疫情 SEIR模型
Python小白的数学建模课-B6. 新冠疫情 SEIR改进模型
Python数模笔记-PuLP库
Python数模笔记-StatsModels统计回归
Python数模笔记-Sklearn
Python数模笔记-NetworkX
Python数模笔记-模拟退火算法