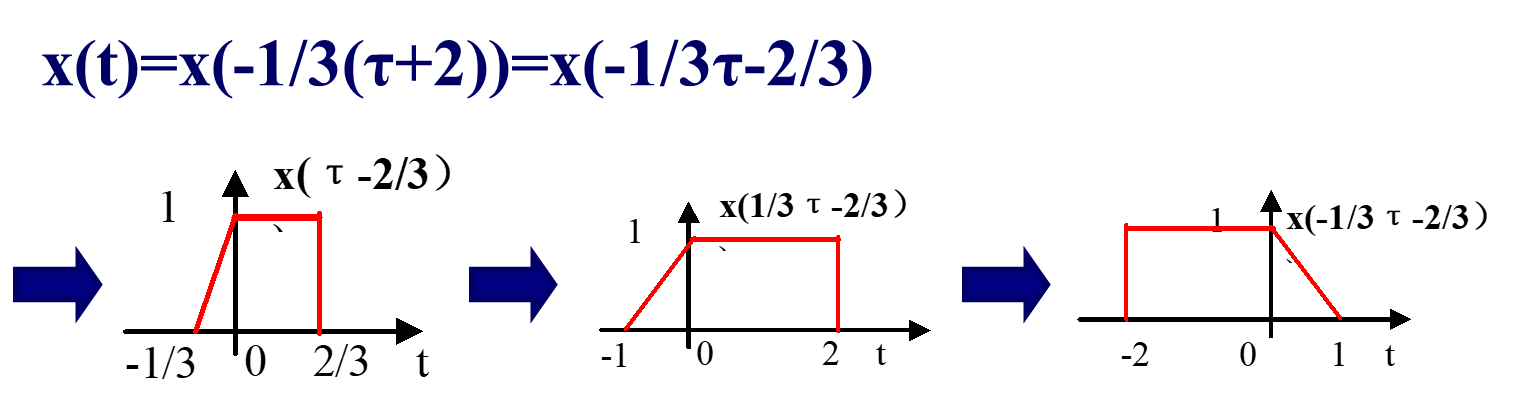信号的运算与变换
目录
前言
《信号与系统》是一门很难的课,也是许多学校考研要考的专业课,由于每周只有两节课,所以每次上完都要及时的去复习,这里参考的教材是奥本海姆著作,刘海棠译,北京:电子工业出版社,2013年。
本章内容介绍
信号与系统分析当中一个重要的概念是关于信号的变化概念。例如,在飞机控制系统中对应于驾驶员动作的信号,经由电和机械的系统变换为飞行推力或飞机控制翼面(如舵或副翼)位置上的改变,进而再进过该机体的动力学和运动学原来变换为飞机速度和航行上的方向上的变化。在这里,我们只关注很有限但很重要的几种最基本的信号变换,且只涉及自变量的简单变换。
信号的运算与变换
在信号的传输及处理过程中往往需要进行信号的运算,包括相加、相乘、移位、反折、尺度变换、以及(微分)差分和积分(累加)等等。
-
相加
两个(或多个)信号之和构成另一个信号,它在任意瞬间的值等于两个或多个信号在同一瞬间的代数和。
连续:x(t)=x1(t)+x2(t)
离散:y[n]=x1[n]+x2[n]
这里就是对应的地方进行相加,只是需要注意离散只有整数有效。
-
相乘
指的是两个(或多个)信号相乘构成另一个信号时,把所有相同瞬间的值一一相乘。
连续:x(t)=x1(t)x2(t)
离散:y[n]=x1[n]x2[n]
与相加有些相同,对应的部分对其进行相乘。
-
时移
遵循一个原则"左加右减",且时移后,形状、幅度不变。
连续信号x(t),设t0>0
x(t-t0),则原信号向右平移t0时间;
x(t-t0),则原信号向左平移t0时间;
离散信号x[n],当m>0
x[n-m]:右移m位
x[n+m]:左移m位
-
反折
即为x(-t),将x(t)沿纵坐标进行反折。
实际就是沿着y轴方向进行对称绘制。
-
尺度变换
将信号x(t)的自变量乘以正系数a为x(at),则:
a>1,将波形进行压缩;
a<1,将波形进行扩展;
压缩和扩展提现在x轴上。
举一个实例:
若x(t)是已录制声音的磁带:
x(-t)表示磁带倒转播放产生的信号
x(2t)表示磁带以二倍速加快播放的结果
x(t/2)表示原磁带放音速度降至一半产生的信号
-
微分(差分)
微分(Differential)
差分(Difference)
一阶前向差分定义为:
一阶后向差分定义为:
-
积分(累加)
积分(Integration)
累加(accumulation)
-
信号的奇偶求解
对于连续信号:
,
则有:
有上面的式子,可以有这样的结论:
对于离散信号也是同样如此。
信号与其偶分量和奇分量之间还满足以下能量关系:
连续信号:
离散信号:
例题:已知下图为x(t),求、
:

-
信号的实虚分解
则:
合适的例题
既然已经了解了上面的知识,做做这里的例题巩固一下吧。
1、时移+反折
求:x(-t+2)
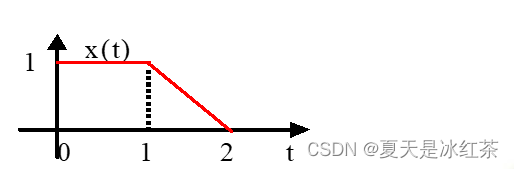

2、时移+尺度
求:x(3t-2)

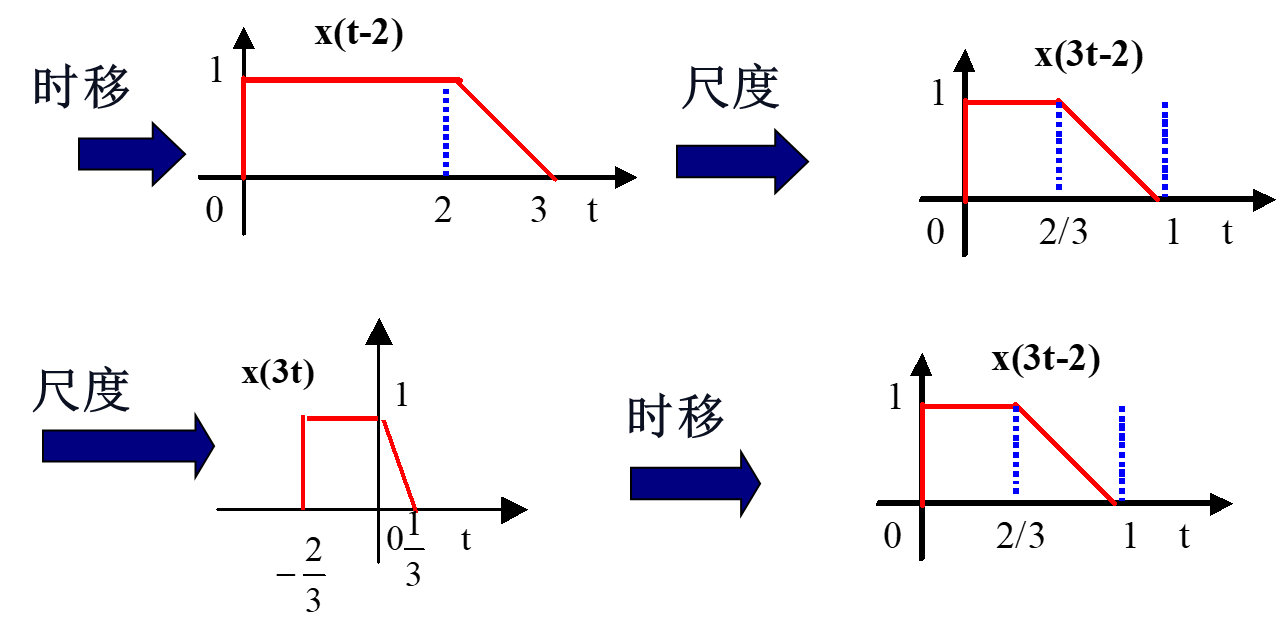
3、时移+反折+尺度
求:x(-3t-2)
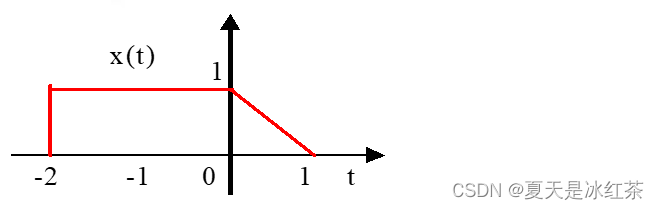
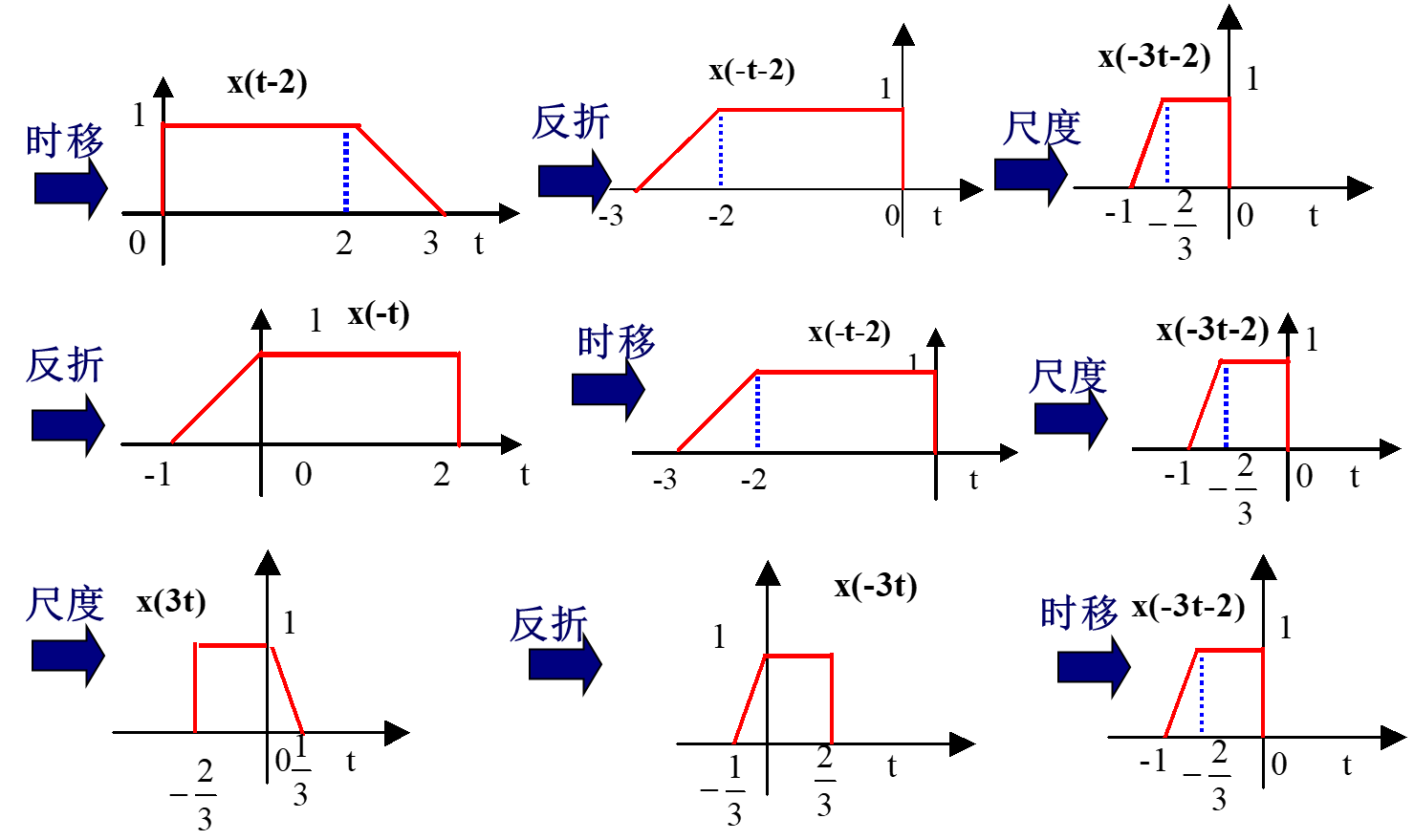
4、反求x(t)
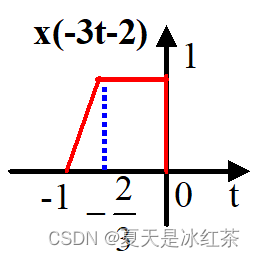
解1:反折-尺度-时移
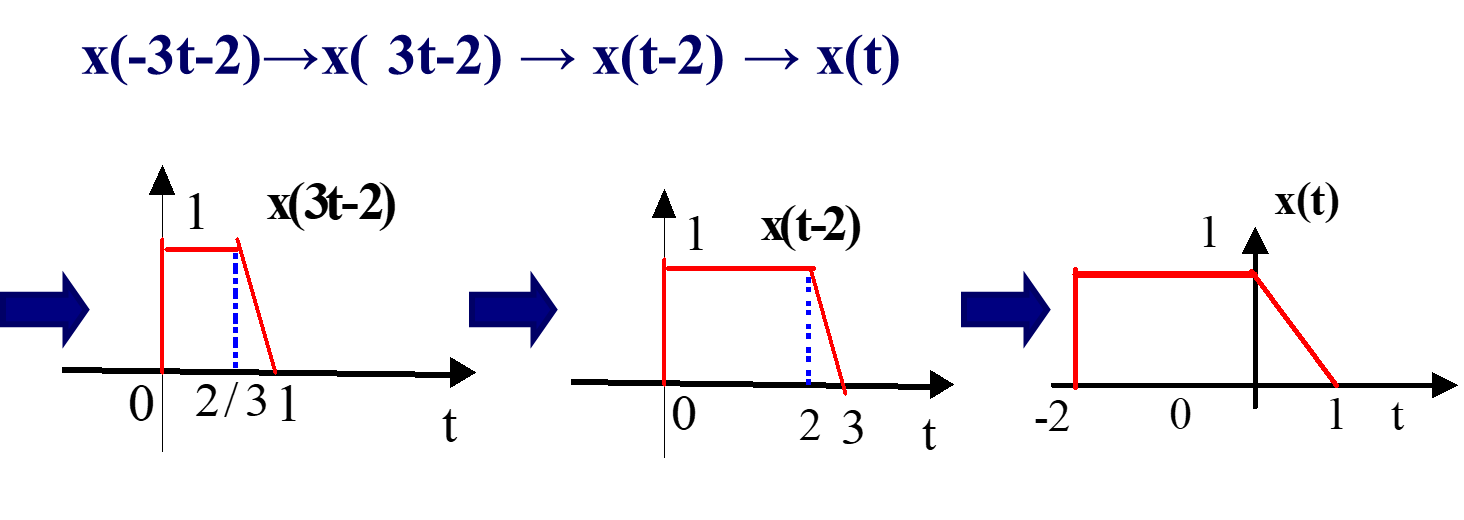
解2:令