一、判断系统是否 " 非时变 "

---

1、案例二

给定 输入序列 x ( n ) = { 0 , 1 , 2 , 3 , 4 , 5 , 0 } x(n) = \{ 0, 1 , 2, 3, 4, 5 , 0 \} x(n)={0,1,2,3,4,5,0} , $n$ 取值 $-1$ ~ $5$

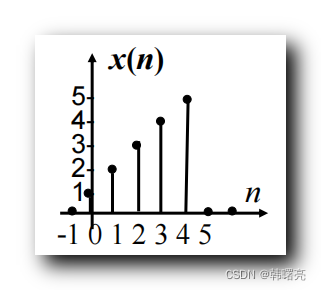
判断其输出序列 $y(n)=x(n^2)$ 的 " 变换 " 操作是否是 " 时不变 " 的 ;

$y(n)=x(n^2)$ 变换操作 :

$y(n)$ 只有在 $n=-1,0,1,2$ 取值时 , 才有值 ,

如果 $n=3$ , $n^2=9$ , $x(9)$ 没有值 ;
如果 $n=4$ , $n^2=16$ , $x(16)$ 没有值 ;
如果 $n=5$ , $n^2=25$ , $x(10)$ 没有值 ;

因此 , 正常变换后 , $y(n)$ 的取值是 $n=0,1,2$ 时的取值 ,

当 $n=-1$ 时 , $y(n)=x(n^2)=x((-1{)}^2)=x(1)=2$ ;
当 $n=0$ 时 , $y(n)=x(n^2)=x(0^2)=x(0)=1$ ;
当 $n=1$ 时 , $y(n)=x(n^2)=x(1^2)=x(1)=2$ ;
当 $n=2$ 时 , $y(n)=x(n^2)=x(2^2)=x(4)=5$ ;

其中 $-1$ 和 $1$ 的平方都为 $1$ , 合并成一个 ;

$x(n)$ 正常变换后的取值为 :

y ( n ) = { 1 , 2 , 5 } y(n) = \{ 1, 2, 5 \} y(n)={1,2,5}

① 时不变系统概念

时不变系统 ( time-invariant ) : 系统特性 , 不随着时间的变化而变化 ;

$$y(n-m)=T[x(n-m)]$$

输入延迟后 , 输出也随之延迟 ;

与 " 时不变 " 系统对应的是 " 时变 " 系统 ;

② 先变换后移位

将 " 输出序列 " 进行移位 , 先 " 变换 " 后 " 移位 " ;

先将 " 输入序列 " 进行 " 变换 " 操作 , 得到 " 输出序列 " , 然后对 输出序列 进行 " 移位 " 操作 ;

其中 " 变换 " 指的是 , 离散时间系统 , 将 " 输入序列 " 变换 为 " 输出序列 " , 输入序列 到 输出序列 之间的操作 , 是 " 变换 " ;

变换操作 : 先将 输入序列 $x(n)$ 进行 变换 操作 , 得到 输出序列 $x(n^2)$ ,

移位操作 : 然后 对 $x(n^2)$ 输出序列 进行移位 $n-n_0$ 得到 $x((n-n_0{)}^2)$ ,

完整运算过程如下 :

$$y(n-n_0)=x((n-n_0{)}^2)$$

先变换 , 变换后输出为 :
y ( n ) = { 1 , 2 , 5 } y(n) = \{ 1, 2, 5 \} y(n)={1,2,5}

后移位的取值为 : 向右移一位 ;

y ( n − 1 ) = { 0 , 1 , 2 , 5 } y(n-1) = \{ 0, 1, 2, 5 \} y(n−1)={0,1,2,5}

③ 先移位后变换

将 " 输入序列 " 进行移位 , 先进行移位 , 将 " 输入序列 $x(n)$ " 先进行 " 移位 " 操作 , 得到 新的 " 输入序列 " 为 $x(n-n_0)$ , 然后 对新的输入序列进行 " 变换 " 操作 , 得到 " 输出序列 " ;

变换过程是 $T[x(n-n_0)]=x(n^2-n_0)$ , 变换时 , 只是将 $n$ 值变为 $n^2$ , $n_0$ 值不动 ;

$x(n-n_0)$ 变换时 , 只将 $n$ 乘以 $2$ , $n_0$ 不变 , 变换结果如为 $x(2n-n_0)$ ;

完整过程如下 :

$$T[x(n-n_0)]=x(n^2-n_0)$$

先将 x ( n ) = { 0 , 1 , 2 , 3 , 4 , 5 , 0 } x(n) = \{ 0, 1 , 2, 3, 4, 5 , 0 \} x(n)={0,1,2,3,4,5,0} , $n$ 取值 $-1$ ~ $5$ , 向右移位 , 移位后的序列 :
x ( n ) = { 0 , 1 , 2 , 3 , 4 , 5 } x(n) = \{ 0, 1 , 2, 3, 4, 5 \} x(n)={0,1,2,3,4,5} $n$ 取值 $0$ ~ $6$ , 移位后的序列图式如下 :

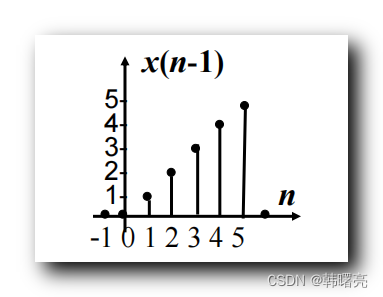
向右移位 1 后 , $n$ 取值 由原来的 $-1$ ~ $5$ 变为了 $0$ ~ $6$ ,

$y(n)$ 只有在 $n=0,1,2$ 取值时 , 才有值 ,

如果 $n=3$ , $n^2=9$ , $x(9)$ 没有值 ;
如果 $n=4$ , $n^2=16$ , $x(16)$ 没有值 ;
如果 $n=5$ , $n^2=25$ , $x(10)$ 没有值 ;

因此 , 正常变换后 , $y(n)$ 的取值是 $n=0,1,2$ 时的取值 ,

当 $n=0$ 时 , $y(n)=x(n^2)=x(0^2)=x(0)=0$ ;
当 $n=1$ 时 , $y(n)=x(n^2)=x(1^2)=x(1)=1$ ;
当 $n=2$ 时 , $y(n)=x(n^2)=x(2^2)=x(4)=4$ ;

$x(n-1)$ 正常变换后的取值为 :

T ( x ( n − 1 ) ) = { 0 , 1 , 4 } T(x(n -1 )) = \{ 0, 1, 4 \} T(x(n−1))={0,1,4}

④ 结论

先 " 变换 " 后 " 移位 " , 结果是 $x((n-n_0{)}^2)$ , 输出序列 为 y ( n − 1 ) = { 0 , 1 , 2 , 5 } y(n-1) = \{ 0, 1, 2, 5 \} y(n−1)={0,1,2,5}

先 " 移位 " 后 " 变换 " , 结果是 $x(n^2-n_0)$ , 输出序列为 T ( x ( n − 1 ) ) = { 0 , 1 , 4 } T(x(n -1 )) = \{ 0, 1, 4 \} T(x(n−1))={0,1,4}

该系统是 " 时变系统 " ;