在社交网络中，个人或单位（结点）之间通过某些关系（边）联系起来。他们受到这些关系的影响，这种影响可以理解为网络中相互连接的结点之间蔓延的一种相互作用，可以增强也可以减弱。而结点根据其所处的位置不同，其在网络中体现的重要性也不尽相同。

“紧密度中心性”是用来衡量一个结点到达其它结点的“快慢”的指标，即一个有较高中心性的结点比有较低中心性的结点能够更快地（平均意义下）到达网络中的其它结点，因而在该网络的传播过程中有更重要的价值。在有N个结点的网络中，结点vi​的“紧密度中心性”Cc(vi​)数学上定义为vi​到其余所有结点vj​ (j=i) 的最短距离d(vi​,vj​)的平均值的倒数：

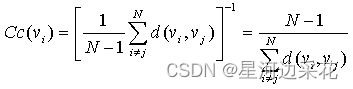
对于非连通图，所有结点的紧密度中心性都是0。

给定一个无权的无向图以及其中的一组结点，计算这组结点中每个结点的紧密度中心性。

输入格式:

输入第一行给出两个正整数N和M，其中N（≤104）是图中结点个数，顺便假设结点从1到N编号；M（≤105）是边的条数。随后的M行中，每行给出一条边的信息，即该边连接的两个结点编号，中间用空格分隔。最后一行给出需要计算紧密度中心性的这组结点的个数K（≤100）以及K个结点编号，用空格分隔。

输出格式:

按照Cc(i)=x.xx的格式输出K个给定结点的紧密度中心性，每个输出占一行，结果保留到小数点后2位。

输入样例:

9 14
1 2
1 3
1 4
2 3
3 4
4 5
4 6
5 6
5 7
5 8
6 7
6 8
7 8
7 9
3 3 4 9

输出样例:

Cc(3)=0.47
Cc(4)=0.62
Cc(9)=0.35

思路：

这道题有好多做法，对于要查询的每个点，每次用一次dijkstra的话也可以，只不过时间复杂度高一点，由于要一个点到其他点的最短距离，每个点用Dijkstra求一遍，或者Floyd算法，其实时间复杂度上都超了，但数据不强（说是1e4,其实最大1e3），勉强能用，科学的办法还是宽搜。

这里提供两种算法：

详细解释一下宽搜，因为边权是1，每次新搜到的点就是上一个点到起点的距离加1，所有点都搜完以后再算总的距离，如果有不可达的点，直接返回-1（表示不可达）即可。

宽搜的实现，使用邻接表存图，一个队列来实现

邻接表模板：

代码一 （宽搜）：

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 200020,M = 10010;
int n, m, q, a, b, x;
int h[N], e[N], ne[N], idx;
int d[M];
bool st[M];
void add(int a, int b) {
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
ll bfs(int x) {
    ll ans = 0;
    memset(st, false, sizeof st);
    memset(d, 0x3f, sizeof d);
    queue<int> q;
    q.push(x);
    st[x] = true;
    d[x]=0;
    while (q.size()) {
        int t = q.front();
        q.pop();

        for (int i = h[t]; i != -1; i = ne[i]) {
            int j = e[i];
            if (!st[j]) {
                d[j] = d[t] + 1;
                st[j] = true;
                q.push(j);
            }
        }
    }
    for (int i = 1; i <= n; i++) {
        if (d[i] == 0x3f3f3f3f)return -1;
        else ans += d[i];
    }
    return ans;
}
int main()
{
    cin >> n >> m;
    memset(h, -1, sizeof h);
    while (m--) {
        cin >> a >> b;
        add(a, b), add(b, a);
    }
    cin >> q;
    bool fg = false;
    for (int i = 0; i < q; i++) {
        cin >> x;
        ll res = 0;
        res = bfs(x);
        if (res == -1) { 
            fg = true;
        }if (fg) {
            printf("Cc(%d)=0.00\n", x);
        }
        else {
            double ans = (double)(n - 1) / res;
            printf("Cc(%d)=%.2lf\n", x, ans);
        }
    }
}

代码二（Floyd算法）：

#include <bits/stdc++.h>
using namespace std;
const int N = 1010, M = 10010, INF = 1e9;
long long res = 0;
int n, m, q , x;
int d[N][N];
void floyd() {
    for (int k = 1; k <= n; k++) {
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= n; j++) {
                d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
            }
        }
    }
}

int main() {
    cin >> n >> m;
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= n; j++) {
            if (i == j)d[i][j] = 0;
            else d[i][j] = INF;
        }
    }
    for (int i = 0; i < m; i++) {
        int a, b;
        cin >> a >> b;
        d[a][b] = d[b][a] = 1;
    }
    floyd();
    cin >> q;
    bool fg = false;
    for (int i = 0; i < q; i++) {
        res = 0;
        cin >> x;
        if(!fg)
        for (int j = 1; j <= n; j++) {
            if (x == j)continue;
            if (d[x][j] > INF / 2) {
                fg = true;
                break;
            }
            res += d[x][j];
        }
        if (fg)printf("Cc(%d)=0.00\n", x);
        else {
            double ans = (double)(n - 1) / res;
            printf("Cc(%d)=%.2lf\n", x, ans);
        }
    }
	return 0;
}