广义最小残量法
Arnoldi迭代
目标:得到一组标准正交基
v
1
,
⋯
,
v
m
\mathbf{v}_1,\cdots,\mathbf{v}_m
v1,⋯,vm,使得
K
m
(
A
,
r
0
)
=
span
{
v
1
,
⋯
,
v
m
}
\mathcal{K}_m\left(\mathbf{A},\mathbf{r}_0\right)=\operatorname{span}\left\{\mathbf{v}_1,\cdots,\mathbf{v}_m\right\}
Km(A,r0)=span{v1,⋯,vm}
显然
v
1
=
r
0
∥
r
0
∥
\mathbf{v}_1=\frac{\mathbf{r}_0}{\|\mathbf{r}_0\|}
v1=∥r0∥r0
假设已经得到
K
j
(
A
,
r
0
)
=
span
(
v
1
,
⋯
,
v
j
)
\mathcal{K}_j\left(\mathbf{A},\mathbf{r}_0\right)=\operatorname{span}\left(\mathbf{v}_1,\cdots,\mathbf{v}_j\right)
Kj(A,r0)=span(v1,⋯,vj)
现在要求
v
j
+
1
\mathbf{v}_{j+1}
vj+1
v
j
∈
K
j
(
A
,
r
0
)
⇒
A
v
j
∈
A
K
j
(
A
,
r
0
)
⊂
K
j
+
1
(
A
,
r
0
)
\mathbf{v}_j\in\mathcal{K}_j\left(\mathbf{A},\mathbf{r}_0\right)\Rightarrow\mathbf{A}\mathbf{v}_j\in \mathbf{A}\mathcal{K}_j\left(\mathbf{A},\mathbf{r}_0\right)\subset\mathcal{K}_{j+1}\left(\mathbf{A},\mathbf{r}_0\right)
vj∈Kj(A,r0)⇒Avj∈AKj(A,r0)⊂Kj+1(A,r0)
那么
A
v
j
=
∑
i
=
0
j
+
1
h
i
j
v
i
\mathbf{A}\mathbf{v}_j=\sum_{i=0}^{j+1}h_{ij}\mathbf{v}_i
Avj=i=0∑j+1hijvi
v
i
T
A
v
j
=
h
i
j
(
i
=
0
,
1
,
⋯
,
j
)
\mathbf{v}_i^T\mathbf{A}\mathbf{v}_j=\mathbf{h}_{ij}\left(i=0,1,\cdots,j\right)
viTAvj=hij(i=0,1,⋯,j)
于是
h
j
+
1
,
j
v
j
+
1
=
A
v
j
−
∑
i
=
0
j
h
i
j
v
j
h_{j+1,j}\mathbf{v}_{j+1}=\mathbf{A}\mathbf{v}_j-\sum_{i=0}^{j}h_{ij}\mathbf{v}_j
hj+1,jvj+1=Avj−i=0∑jhijvj
所以
{
v
j
+
1
=
A
v
j
−
∑
i
=
0
j
h
i
j
v
j
∥
A
v
j
−
∑
i
=
0
j
h
i
j
v
j
∥
h
j
+
1
,
j
=
∥
A
v
j
−
∑
i
=
0
j
h
i
j
v
j
∥
\begin{cases} \mathbf{v}_{j+1}=\frac{\mathbf{A}\mathbf{v}_j-\sum_{i=0}^{j}h_{ij}\mathbf{v}_j}{\|\mathbf{A}\mathbf{v}_j-\sum_{i=0}^{j}h_{ij}\mathbf{v}_j\|}\\ h_{j+1,j}=\|\mathbf{A}\mathbf{v}_j-\sum_{i=0}^{j}h_{ij}\mathbf{v}_j\|\\ \end{cases}
⎩
⎨
⎧vj+1=∥Avj−∑i=0jhijvj∥Avj−∑i=0jhijvjhj+1,j=∥Avj−∑i=0jhijvj∥
如果某一轮迭代中,
h
j
+
1
,
j
=
0
h_{j+1,j}=0
hj+1,j=0,则可以提前停止
可以证明Arnoldi迭代提前停止,当且仅当
dim
K
k
<
k
\operatorname{dim}\mathcal{K}_k<k
dimKk<k
令
q
m
(
A
)
q_m\left(\mathbf{A}\right)
qm(A)是
m
m
m阶多项式
v
1
=
q
0
(
A
)
v
1
\mathbf{v}_1=q_0\left(\mathbf{A}\right)\mathbf{v}_1
v1=q0(A)v1
假设当
i
≤
j
i\le j
i≤j时,
v
j
=
q
j
−
1
(
A
)
v
1
\mathbf{v}_j=q_{j-1}\left(\mathbf{A}\right)\mathbf{v}_1
vj=qj−1(A)v1成立,则
h
j
+
1
,
j
v
j
+
1
=
A
v
j
−
∑
i
=
0
j
h
i
j
v
j
=
q
j
+
1
(
A
)
v
1
h_{j+1,j}\mathbf{v}_{j+1}=\mathbf{A}\mathbf{v}_j-\sum_{i=0}^{j}h_{ij}\mathbf{v}_j=q_{j+1}\left(\mathbf{A}\right)\mathbf{v}_1
hj+1,jvj+1=Avj−∑i=0jhijvj=qj+1(A)v1
也就是说,只要没有提前停止,就有
K
m
(
A
,
r
0
)
=
span
{
v
1
,
⋯
,
v
m
}
\mathcal{K}_m\left(\mathbf{A},\mathbf{r}_0\right)=\operatorname{span}\left\{\mathbf{v}_1,\cdots,\mathbf{v}_m\right\}
Km(A,r0)=span{v1,⋯,vm}

Arnoldi迭代最后会产生一个Hessenberg矩阵
H
ˉ
∈
R
(
k
+
1
)
×
k
\bar{\mathbf{H}}\in\mathbb{R}^{\left(k+1\right)\times k}
Hˉ∈R(k+1)×k
使得
A
V
m
=
V
m
+
1
H
ˉ
m
=
V
m
H
m
+
v
m
+
1
(
h
m
+
1
,
m
e
m
T
)
=
V
m
H
m
+
w
m
e
m
T
V
m
T
A
V
m
=
H
m
\begin{aligned} \mathbf{A}\mathbf{V}_m &=\mathbf{V}_{m+1}\bar{\mathbf{H}}_m\\ &=\mathbf{V}_m\mathbf{H}_m+\mathbf{v}_{m+1}\left(h_{m+1,m}\mathbf{e}_m^T\right)\\ &=\mathbf{V}_m\mathbf{H}_m+\mathbf{w}_m\mathbf{e}_m^T\\ \mathbf{V}_m^T\mathbf{A}\mathbf{V}_m &=\mathbf{H}_m \end{aligned}
AVmVmTAVm=Vm+1Hˉm=VmHm+vm+1(hm+1,memT)=VmHm+wmemT=Hm
其中
H
m
\mathbf{H}_m
Hm是
H
ˉ
m
\bar{\mathbf{H}}_m
Hˉm的前
m
m
m行
注意
V
k
+
1
T
V
k
+
1
=
I
\mathbf{V}_{k+1}^T\mathbf{V}_{k+1}=\mathbf{I}
Vk+1TVk+1=I,但是
V
k
+
1
V
k
+
1
T
\mathbf{V}_{k+1}\mathbf{V}_{k+1}^T
Vk+1Vk+1T不一定等于单位矩阵
修改版

主要区别就是
h
i
j
=
(
w
j
,
v
i
)
h_{ij}=\left(w_j,v_i\right)
hij=(wj,vi),因为
v
i
T
v
j
=
0
\mathbf{v}_i^T\mathbf{v}_j=0
viTvj=0,所以数值上是一样的
Householder变换

其中3-5行是产生Householder的反射矩阵
其实相当于对 v , A v 1 , A v 2 , ⋯ , A v m \mathbf{v},\mathbf{A}\mathbf{v}_1,\mathbf{A}\mathbf{v}_2,\cdots,\mathbf{A}\mathbf{v}_m v,Av1,Av2,⋯,Avm做householder正交化或者householder版QR分解
令
Q
j
=
P
j
P
j
−
1
⋯
P
1
\mathbf{Q}_j=\mathbf{P}_j\mathbf{P}_{j-1}\cdots\mathbf{P}_1
Qj=PjPj−1⋯P1
由第8行
Q
j
A
v
j
=
z
j
+
1
\mathbf{Q}_j\mathbf{A}\mathbf{v}_j=\mathbf{z}_{j+1}\\
QjAvj=zj+1
由第6行
h
j
=
P
j
+
1
z
j
+
1
=
P
j
+
1
Q
j
A
v
j
=
Q
j
+
1
A
v
j
\mathbf{h}_j=\mathbf{P}_{j+1}\mathbf{z}_{j+1}=\mathbf{P}_{j+1}\mathbf{Q}_j\mathbf{A}\mathbf{v}_j=\mathbf{Q}_{j+1}\mathbf{A}\mathbf{v}_j
hj=Pj+1zj+1=Pj+1QjAvj=Qj+1Avj
注意到
h
j
\mathbf{h}_{j}
hj的
j
+
1
,
⋯
,
n
j+1,\cdots,n
j+1,⋯,n分量都是
0
0
0,所以
P
i
h
j
=
h
j
(
i
≥
j
+
2
)
\mathbf{P}_i\mathbf{h}_j=\mathbf{h}_j\left(i\ge j+2\right)
Pihj=hj(i≥j+2),于是
h
j
=
P
m
⋯
P
j
+
2
h
j
=
Q
m
A
v
j
\mathbf{h}_j=\mathbf{P}_m\cdots\mathbf{P}_{j+2}\mathbf{h}_j=\mathbf{Q}_m\mathbf{A}\mathbf{v}_j
hj=Pm⋯Pj+2hj=QmAvj
于是
Q
m
(
v
,
A
v
1
,
⋯
,
A
v
m
)
=
(
h
0
,
⋯
,
h
m
)
\mathbf{Q}_m\left(\mathbf{v},\mathbf{A}\mathbf{v}_1,\cdots,\mathbf{A}\mathbf{v}_m\right)=\left(\mathbf{h}_0,\cdots,\mathbf{h}_m\right)
Qm(v,Av1,⋯,Avm)=(h0,⋯,hm)
(
h
0
,
⋯
,
h
m
)
\left(\mathbf{h}_0,\cdots,\mathbf{h}_m\right)
(h0,⋯,hm)是
n
×
(
m
+
1
)
n\times \left(m+1\right)
n×(m+1)的矩阵,
Q
m
\mathbf{Q}_m
Qm是标准正交矩阵
令
H
ˉ
m
\bar{\mathbf{H}}_m
Hˉm为
(
h
1
,
⋯
,
h
m
)
\left(\mathbf{h}_1,\cdots,\mathbf{h}_m\right)
(h1,⋯,hm)的前
m
+
1
m+1
m+1行
A
v
j
=
Q
j
+
1
T
h
j
=
Q
j
+
1
T
∑
i
=
1
j
+
1
h
i
j
e
i
=
∑
i
=
1
j
+
1
h
i
j
Q
j
+
1
T
e
i
\mathbf{A}\mathbf{v}_j=\mathbf{Q}_{j+1}^T\mathbf{h}_j=\mathbf{Q}_{j+1}^T\sum_{i=1}^{j+1}h_{ij}\mathbf{e}_i=\sum_{i=1}^{j+1}h_{ij}\mathbf{Q}_{j+1}^T\mathbf{e}_i
Avj=Qj+1Thj=Qj+1Ti=1∑j+1hijei=i=1∑j+1hijQj+1Tei
注意到
P
k
e
i
=
e
i
(
i
<
k
)
\mathbf{P}_k\mathbf{e}_i=\mathbf{e}_i\left(i<k\right)
Pkei=ei(i<k)
Q
j
+
1
T
e
i
=
P
1
⋯
P
j
+
1
e
i
=
v
i
(
i
≤
j
+
1
)
\mathbf{Q}_{j+1}^T\mathbf{e}_i=\mathbf{P}_1\cdots\mathbf{P}_{j+1}\mathbf{e}_i=\mathbf{v}_i\left(i\le j+1\right)
Qj+1Tei=P1⋯Pj+1ei=vi(i≤j+1)
于是
A
v
j
=
∑
i
=
1
j
+
1
h
i
j
v
i
\mathbf{A}\mathbf{v}_j=\sum_{i=1}^{j+1}h_{ij}\mathbf{v}_i
Avj=i=1∑j+1hijvi
所以
A
V
m
=
V
m
+
1
H
ˉ
m
\mathbf{A}\mathbf{V}_m=\mathbf{V}_{m+1}\bar{\mathbf{H}}_m
AVm=Vm+1Hˉm
广义极小残量法
广义极小残量法(Generalized Minimal RESidual,GMRES)
考虑大型线性方程组
A
x
=
b
\mathbf{Ax}=\mathbf{b}
Ax=b
考虑Krylov子空间
K
m
(
A
,
r
0
)
=
span
{
r
0
,
A
r
0
,
⋯
,
A
m
−
1
r
0
}
\mathcal{K}_m\left(\mathbf{A},\mathbf{r}_0\right)=\operatorname{span}\left\{\mathbf{r}_0,\mathbf{A}\mathbf{r}_0,\cdots,\mathbf{A}^{m-1}\mathbf{r}_0\right\}
Km(A,r0)=span{r0,Ar0,⋯,Am−1r0}
设
x
(
0
)
\mathbf{x}^{(0)}
x(0)为起点
GMRES考虑解
min
x
∈
x
(
0
)
+
K
m
(
A
,
r
0
)
∥
A
x
−
b
∥
\min\limits_{\mathbf{x}\in \mathbf{x}^{(0)}+\mathcal{K}_m\left(\mathbf{A},\mathbf{r}_0\right)}\|\mathbf{A}\mathbf{x}-\mathbf{b}\|
x∈x(0)+Km(A,r0)min∥Ax−b∥
设
v
1
,
⋯
,
v
m
\mathbf{v}_1,\cdots,\mathbf{v}_m
v1,⋯,vm为一组标准正交基
V
m
=
(
v
1
,
⋯
,
v
m
)
∈
R
n
×
m
\mathbf{V}_m=\left(\mathbf{v}_1,\cdots,\mathbf{v}_m\right)\in\mathbb{R}^{n\times m}
Vm=(v1,⋯,vm)∈Rn×m
则
x
(
m
)
∈
x
(
0
)
+
K
m
(
A
,
r
0
)
\mathbf{x}^{(m)}\in\mathbf{x}^{(0)}+\mathcal{K}_m\left(\mathbf{A},\mathbf{r}_0\right)
x(m)∈x(0)+Km(A,r0)可以写作
x
(
m
)
=
x
(
0
)
−
V
m
y
\mathbf{x}^{(m)}=\mathbf{x}^{(0)}-\mathbf{V}_m\mathbf{y}
x(m)=x(0)−Vmy,其中
y
∈
R
m
\mathbf{y}\in\mathbb{R}^m
y∈Rm
由Arnoldi迭代
b
−
A
x
=
b
−
A
(
x
(
0
)
+
V
m
y
)
=
r
0
−
A
V
m
y
=
β
v
1
−
V
m
+
1
H
ˉ
m
y
=
V
m
+
1
(
β
e
1
−
H
ˉ
m
y
)
\begin{aligned} \mathbf{b}-\mathbf{Ax} &= \mathbf{b}-\mathbf{A}\left(\mathbf{x}^{(0)}+\mathbf{V}_m\mathbf{y}\right)\\ &= \mathbf{r}_0-\mathbf{A}\mathbf{V}_m\mathbf{y}\\ &= \beta \mathbf{v}_1-\mathbf{V}_{m+1}\bar{\mathbf{H}}_m\mathbf{y}\\ &=\mathbf{V}_{m+1}\left(\beta\mathbf{e}_1-\bar{\mathbf{H}}_m\mathbf{y}\right) \end{aligned}
b−Ax=b−A(x(0)+Vmy)=r0−AVmy=βv1−Vm+1Hˉmy=Vm+1(βe1−Hˉmy)
其中
r
0
=
b
−
A
x
(
0
)
,
β
=
∥
r
0
∥
,
v
1
=
r
0
β
\mathbf{r}_0=\mathbf{b}-\mathbf{A}\mathbf{x}^{(0)},\beta=\|\mathbf{r}_0\|,\mathbf{v}_1=\frac{\mathbf{r}_0}{\beta}
r0=b−Ax(0),β=∥r0∥,v1=βr0
于是
min
x
∈
x
(
0
)
+
K
m
(
A
,
r
0
)
∥
A
x
−
b
∥
=
min
y
∈
R
m
∥
r
0
−
A
V
m
y
∥
=
min
y
∈
R
m
∥
β
e
1
−
H
ˉ
m
y
∥
\min\limits_{\mathbf{x}\in \mathbf{x}^{(0)}+\mathcal{K}_m\left(\mathbf{A},\mathbf{r}_0\right)}\|\mathbf{A}\mathbf{x}-\mathbf{b}\|=\min\limits_{\mathbf{y}\in\mathbb{R}^m}\|\mathbf{r}_0-\mathbf{A}\mathbf{V}_m\mathbf{y}\|=\min\limits_{\mathbf{y}\in\mathbb{R}^m} \|\beta\mathbf{e}_1-\bar{\mathbf{H}}_m\mathbf{y}\|
x∈x(0)+Km(A,r0)min∥Ax−b∥=y∈Rmmin∥r0−AVmy∥=y∈Rmmin∥βe1−Hˉmy∥
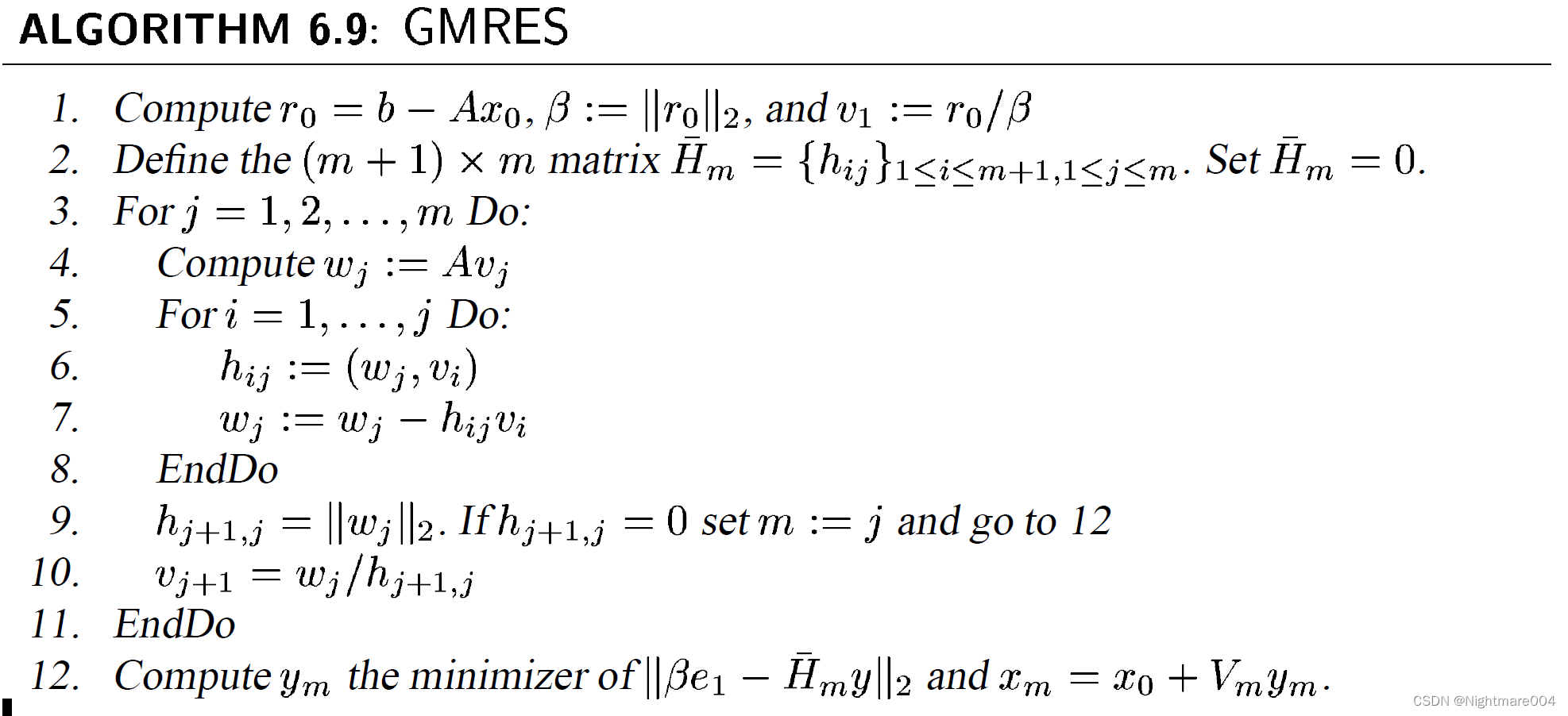
Arnoldi-Householder
设
y
m
=
(
η
1
⋮
η
m
)
\mathbf{y}_m=\begin{pmatrix} \eta_1\\ \vdots\\ \eta_m \end{pmatrix}
ym=⎝
⎛η1⋮ηm⎠
⎞
则
x
(
m
)
=
x
(
0
)
+
η
1
v
1
+
⋯
+
η
m
v
m
\mathbf{x}^{(m)}=\mathbf{x}^{(0)}+\eta_1\mathbf{v}_1+\cdots+\eta_m\mathbf{v}_m
x(m)=x(0)+η1v1+⋯+ηmvm
因为
v
j
=
P
1
⋯
P
j
e
j
\mathbf{v}_j=\mathbf{P}_1\cdots\mathbf{P}_j\mathbf{e}_j
vj=P1⋯Pjej
所以
x
(
m
)
=
x
(
0
)
+
η
1
v
1
+
⋯
+
η
m
v
m
=
x
(
0
)
+
η
1
P
1
e
1
+
⋯
+
η
m
P
1
⋯
P
m
e
m
=
x
(
0
)
+
P
1
(
η
1
e
1
+
P
2
(
η
2
e
2
+
⋯
P
m
−
1
(
η
m
−
1
e
m
−
1
+
P
m
η
m
e
m
)
)
)
\begin{aligned} \mathbf{x}^{(m)} &= \mathbf{x}^{(0)}+\eta_1\mathbf{v}_1+\cdots+\eta_m\mathbf{v}_m\\ &=\mathbf{x}^{(0)}+\eta_1\mathbf{P}_1\mathbf{e}_1+\cdots+\eta_m\mathbf{P}_1\cdots\mathbf{P}_m\mathbf{e}_m\\ &=\mathbf{x}^{(0)}+\mathbf{P}_1\left(\eta_1\mathbf{e}_1+\mathbf{P}_2\left(\eta_2\mathbf{e}_2+\cdots\mathbf{P}_{m-1}\left(\eta_{m-1}\mathbf{e}_{m-1}+\mathbf{P}_m\eta_m\mathbf{e}_m\right)\right)\right) \end{aligned}
x(m)=x(0)+η1v1+⋯+ηmvm=x(0)+η1P1e1+⋯+ηmP1⋯Pmem=x(0)+P1(η1e1+P2(η2e2+⋯Pm−1(ηm−1em−1+Pmηmem)))
最后就可以减小代价

进一步化简
使用Givens旋转变换,把Hessenberg矩阵
H
ˉ
m
\bar{\mathbf{H}}_m
Hˉm化成上三角矩阵加一行
0
0
0
设
Ω
i
\Omega_i
Ωi为第
i
i
i个旋转矩阵
Q
m
=
Ω
m
Ω
m
−
1
⋯
Ω
1
R
ˉ
m
=
Q
m
H
ˉ
m
g
ˉ
m
=
Q
m
(
β
e
1
)
=
(
γ
1
,
⋯
,
γ
m
+
1
)
T
\mathbf{Q}_m=\Omega_m\Omega_{m-1}\cdots\Omega_1\\ \bar{\mathbf{R}}_m=\mathbf{Q}_m\bar{\mathbf{H}}_m\\ \bar{\mathbf{g}}_m=\mathbf{Q}_m\left(\beta\mathbf{e}_1\right)=\left(\gamma_1,\cdots,\gamma_{m+1}\right)^T
Qm=ΩmΩm−1⋯Ω1Rˉm=QmHˉmgˉm=Qm(βe1)=(γ1,⋯,γm+1)T
于是
min
y
∈
R
m
∥
β
e
1
−
H
ˉ
m
y
∥
=
min
y
∈
R
m
∥
g
ˉ
m
−
R
ˉ
m
y
∥
\min\limits_{\mathbf{y}\in\mathbb{R}^m} \|\beta\mathbf{e}_1-\bar{\mathbf{H}}_m\mathbf{y}\|=\min\limits_{\mathbf{y}\in\mathbb{R}^m} \|\bar{\mathbf{g}}_m-\bar{\mathbf{R}}_m\mathbf{y}\|
y∈Rmmin∥βe1−Hˉmy∥=y∈Rmmin∥gˉm−Rˉmy∥
令
R
m
\mathbf{R}_m
Rm为
R
ˉ
m
\bar{\mathbf{R}}_m
Rˉm删掉最后一行,
g
m
=
(
γ
1
⋮
γ
m
)
\mathbf{g}_m=\begin{pmatrix} \gamma_1\\ \vdots\\ \gamma_m \end{pmatrix}
gm=⎝
⎛γ1⋮γm⎠
⎞
∥
g
ˉ
m
−
R
ˉ
m
y
∥
2
=
∥
g
m
−
R
m
y
∥
2
+
∣
γ
m
+
1
∣
2
\begin{aligned} \|\bar{\mathbf{g}}_m-\bar{\mathbf{R}}_m\mathbf{y}\|^2 &= \|\mathbf{g}_m-\mathbf{R}_m\mathbf{y}\|^2+\left|\gamma_{m+1}\right|^2 \end{aligned}
∥gˉm−Rˉmy∥2=∥gm−Rmy∥2+∣γm+1∣2
A
V
m
=
V
m
+
1
H
ˉ
m
=
V
m
+
1
Q
m
T
R
ˉ
m
⇒
rank
(
A
V
m
)
=
rank
(
R
ˉ
m
)
\mathbf{A}\mathbf{V}_m=\mathbf{V}_{m+1}\bar{\mathbf{H}}_m=\mathbf{V}_{m+1}\mathbf{Q}_m^T\bar{\mathbf{R}}_m\Rightarrow\operatorname{rank}\left(\mathbf{A}\mathbf{V}_m\right)=\operatorname{rank}\left(\bar{\mathbf{R}}_m\right)
AVm=Vm+1Hˉm=Vm+1QmTRˉm⇒rank(AVm)=rank(Rˉm)
所以只要
r
i
i
≠
0
r_{ii}\neq 0
rii=0,
A
V
m
\mathbf{A}\mathbf{V}_m
AVm非奇异
因为
R
m
\mathbf{R}_m
Rm是上三角矩阵,可以通过回代解,
y
m
=
R
m
−
1
g
m
\mathbf{y}_m=\mathbf{R}_m^{-1}\mathbf{g}_m
ym=Rm−1gm
min
y
∈
R
m
∥
g
ˉ
m
−
R
ˉ
m
y
∥
=
∣
γ
m
+
1
∣
\min\limits_{\mathbf{y}\in\mathbb{R}^m} \|\bar{\mathbf{g}}_m-\bar{\mathbf{R}}_m\mathbf{y}\|=\left|\gamma_{m+1}\right|
y∈Rmmin∥gˉm−Rˉmy∥=∣γm+1∣
重启
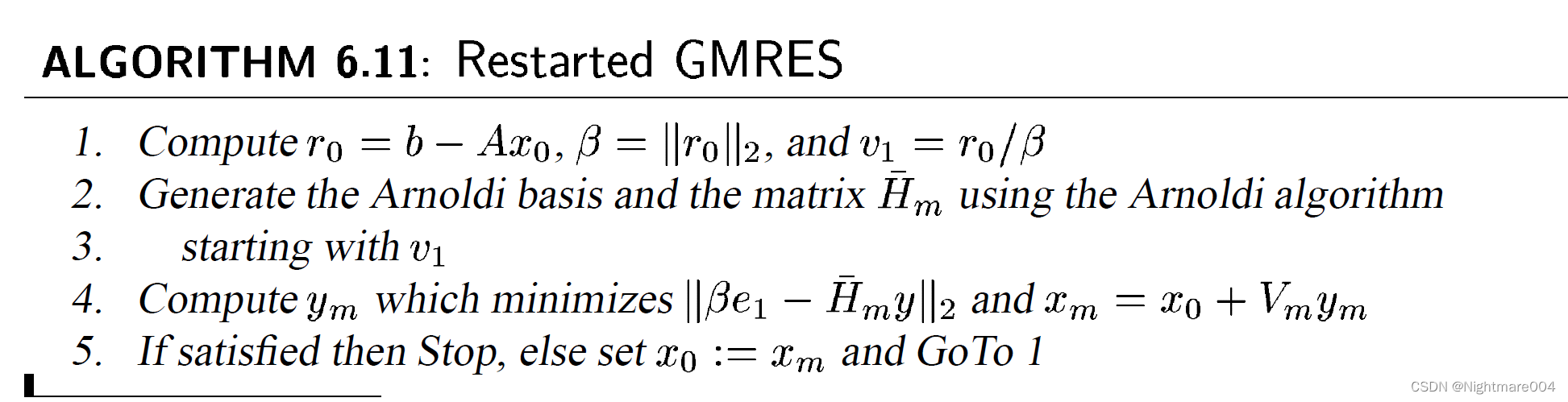
收敛性
假设
A
\mathbf{A}
A可对角化,即
A
=
X
Λ
X
−
1
\mathbf{A}=\mathbf{X}\Lambda\mathbf{X}^{-1}
A=XΛX−1
其中
Λ
=
diag
(
λ
1
,
⋯
,
λ
n
)
\Lambda=\operatorname{diag}\left(\lambda_1,\cdots,\lambda_n\right)
Λ=diag(λ1,⋯,λn)是
A
\mathbf{A}
A的特征值组成的对角矩阵
令
ϵ
(
m
)
=
min
p
∈
P
m
,
p
(
0
)
=
1
max
i
=
1
,
⋯
,
n
∣
p
(
λ
i
)
∣
\epsilon^{(m)}=\min_{p\in\mathbb{P}_m,p\left(0\right)=1}\max_{i=1,\cdots,n}\left|p\left(\lambda_i\right)\right|
ϵ(m)=p∈Pm,p(0)=1mini=1,⋯,nmax∣p(λi)∣
则
∥
r
m
∥
≤
κ
2
(
x
)
ϵ
(
m
)
∥
r
0
∥
\|\mathbf{r}_m\|\le \kappa_2\left(\mathbf{x}\right)\epsilon^{(m)}\|\mathbf{r}_0\|
∥rm∥≤κ2(x)ϵ(m)∥r0∥
证明:因为
x
∈
K
m
\mathbf{x}\in\mathcal{K}_m
x∈Km,有
b
−
A
x
=
p
(
A
)
r
0
\mathbf{b}-\mathbf{Ax}=p\left(\mathbf{A}\right)\mathbf{r}_0
b−Ax=p(A)r0
∥
b
−
A
x
∥
=
∥
X
p
(
Λ
)
X
−
1
r
0
∥
≤
∥
X
∥
2
∥
X
−
1
∥
2
∥
r
0
∥
∥
p
(
Λ
)
∥
≤
κ
2
(
X
)
ϵ
(
m
)
∥
r
0
∥
\|\mathbf{b}-\mathbf{Ax}\|=\|\mathbf{X}p\left(\Lambda\right)\mathbf{X}^{-1}\mathbf{r}_0\|\le\|\mathbf{X}\|_2\|\mathbf{X}^{-1}\|_2\|\mathbf{r}_0\|\|p\left(\Lambda\right)\|\le\kappa_2\left(\mathbf{X}\right)\epsilon^{(m)}\|\mathbf{r}_0\|
∥b−Ax∥=∥Xp(Λ)X−1r0∥≤∥X∥2∥X−1∥2∥r0∥∥p(Λ)∥≤κ2(X)ϵ(m)∥r0∥
推论
假设
A
\mathbf{A}
A可对角化,即
A
=
X
Λ
X
−
1
\mathbf{A}=\mathbf{X}\Lambda\mathbf{X}^{-1}
A=XΛX−1
其中
Λ
=
diag
(
λ
1
,
⋯
,
λ
n
)
\Lambda=\operatorname{diag}\left(\lambda_1,\cdots,\lambda_n\right)
Λ=diag(λ1,⋯,λn)是
A
\mathbf{A}
A的特征值组成的对角矩阵
假设
A
\mathbf{A}
A的特征值落在椭圆
E
(
c
,
d
,
a
)
E\left(c,d,a\right)
E(c,d,a)中(
c
c
c为中心,
d
d
d为焦距长,
a
a
a为长半轴)
则
∥
r
m
∥
≤
κ
2
(
X
)
C
m
(
a
d
)
∣
C
m
(
c
d
)
∣
∥
r
0
∥
\|\mathbf{r}_m\|\le \kappa_2\left(\mathbf{X}\right)\frac{C_m\left(\frac{a}{d}\right)}{\left|C_m\left(\frac{c}{d}\right)\right|}\|\mathbf{r}_0\|
∥rm∥≤κ2(X)∣
∣Cm(dc)∣
∣Cm(da)∥r0∥
其中
C
C
C为切比雪夫多项式
证明:
摸了
参考
相关文章
- ☆打卡算法☆LeetCode 209. 长度最小的子数组 算法解析
- 广义最小二乘法是加权最小二乘法的特例_简述广义最小二乘法
- 求最大公约数和最小公倍数的算法[通俗易懂]
- 最小二乘法求回归直线方程的推导过程
- 生成树和最小生成树prim,kruskal
- 最小可用maven+springboot 项目(无法使用外网,但是有maven私库情况)
- 【最小表示法】模板级运用的“困难”题
- 最小可行架构注意事项:必须考虑分布式处理和数据的位置
- 每日一题(2022-04-30)—— 最小差值 I
- 【移动端网页布局】移动端网页布局基础概念 ③ ( meta 视口标签简介 | 利用 meta 视口标签 设置 网页宽度 / 是否允许用户缩放 / 初始缩放比例 / 最小缩放比例 / 最大缩放比例 )
- 移植busybox构建最小根文件系统的步骤详解
- 室温下最小尺寸全介质微纳激光问世
- 原则Linux的最小权限原则:安全更稳妥(linux最小权限)
- Oracle特性:最大致胜,最小不失。(oracle最大最小)
- 时间MSSQL源码运行告警最小时间的极限考验(mssql源码运行)
- 世界上最小的磁体诞生!IBM 实现在单原子上存储位数据
- python实现获取序列中最小的几个元素

