pumping lemma
正规语言版本
L
L
L是正规语言,则存在整数
p
≥
1
p\ge 1
p≥1
对于任意长度大于等于
p
p
p的字符串
w
∈
L
w\in L
w∈L,存在一种分解
w
=
x
y
z
w=xyz
w=xyz,满足下面3个条件
∣
y
∣
≥
1
\left|y\right|\ge 1
∣y∣≥1
∣
x
y
∣
≤
p
\left|xy\right|\le p
∣xy∣≤p
∀
n
≥
0
,
x
y
n
z
∈
L
\forall n\ge 0,xy^nz\in L
∀n≥0,xynz∈L
即
(
∀
L
⊆
Σ
∗
)
(
regular
(
L
)
⇒
(
(
∃
p
≥
1
)
(
(
∀
w
∈
L
)
(
(
∣
w
∣
≥
p
)
⇒
(
(
∃
x
,
y
,
z
∈
Σ
∗
)
(
w
=
x
y
z
∧
(
∣
y
∣
≥
1
∧
∣
x
y
∣
≤
p
∧
(
∀
n
≥
0
)
(
x
y
n
z
∈
L
)
)
)
)
)
)
)
)
\begin{aligned} &\left(\forall L \subseteq \Sigma^*\right) \\ &\quad(\text { regular }(L) \Rightarrow \\ &\quad((\exists p \geq 1)((\forall w \in L)((|w| \geq p) \Rightarrow \\ &\left.\left.\left.\left.\quad\left(\left(\exists x, y, z \in \Sigma^*\right)\left(w=x y z \wedge\left(|y| \geq 1 \wedge|x y| \leq p \wedge(\forall n \geq 0)\left(x y^n z \in L\right)\right)\right)\right)\right)\right)\right)\right) \end{aligned}
(∀L⊆Σ∗)( regular (L)⇒((∃p≥1)((∀w∈L)((∣w∣≥p)⇒((∃x,y,z∈Σ∗)(w=xyz∧(∣y∣≥1∧∣xy∣≤p∧(∀n≥0)(xynz∈L))))))))
证明:
根据Myhill–Nerode theorem,正则语言可以转为有限自动机
设这个有限自动机由
p
p
p个状态
对于一个长度大于等于
p
p
p字符串
w
w
w,进入自动机需要经过
p
+
1
p+1
p+1个状态
根据抽屉原理,至少有一个状态被访问两遍,如图
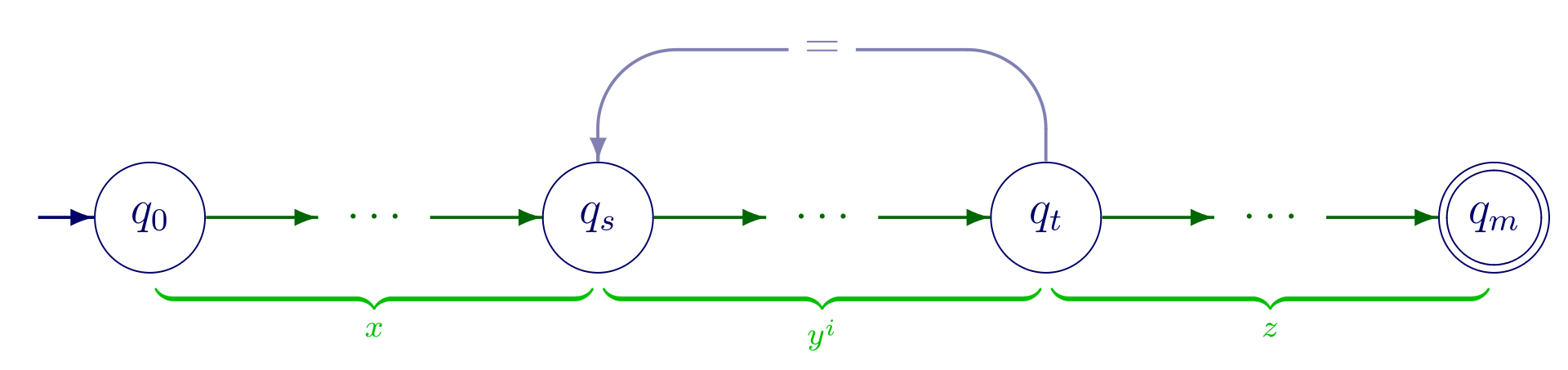
∣
y
∣
≥
1
\left|y\right|\ge 1
∣y∣≥1,因为要有环
∣
x
y
∣
≤
p
\left|xy\right|\le p
∣xy∣≤p,(因为还没走完?
显然
x
y
i
z
∈
L
xy^i z\in L
xyiz∈L
举个例子,比如
L
=
{
0
n
1
n
∣
n
>
0
}
L=\left\{0^n1^n|n>0\right\}
L={0n1n∣n>0}不是正则语言
w
=
0
p
1
p
w=0^p1^p
w=0p1p
因为
∣
x
y
∣
≤
p
\left|xy\right|\le p
∣xy∣≤p,所以
y
∈
0
∗
y\in 0^*
y∈0∗
令
x
=
0
p
−
m
,
y
=
0
m
,
z
=
1
p
(
m
≥
1
)
x=0^{p-m},y=0^m,z=1^p\left(m\ge1\right)
x=0p−m,y=0m,z=1p(m≥1)
于是
w
=
x
y
z
=
0
p
−
m
1
m
1
p
w=xyz=0^{p-m}1^m1^p
w=xyz=0p−m1m1p
而
x
y
0
z
=
x
z
=
0
p
−
m
1
p
∉
L
xy^0z=xz=0^{p-m}1^p\notin L
xy0z=xz=0p−m1p∈/L
另一个例子:
L
=
{
a
b
c
d
}
L=\left\{abcd\right\}
L={abcd}
取
p
=
5
p=5
p=5,因为没有
∣
w
∣
≥
5
\left|w\right|\ge5
∣w∣≥5,所以成立
反过来不一定成立:
L
=
{
a
b
n
c
n
∣
n
≥
1
}
∪
{
a
k
(
b
∣
c
)
∗
∣
k
≠
1
}
L=\left\{ab^nc^n|n\ge1\right\}\cup\left\{a^k(b|c)^*|k\neq 1\right\}
L={abncn∣n≥1}∪{ak(b∣c)∗∣k=1}
选定
p
=
2
p=2
p=2
对于
w
=
a
b
n
c
n
w=ab^nc^n
w=abncn,选择
x
=
ϵ
,
y
=
a
,
z
=
b
n
c
n
x=\epsilon,y=a,z=b^nc^n
x=ϵ,y=a,z=bncn
对于
w
=
(
b
∣
c
)
∗
w=\left(b|c\right)^*
w=(b∣c)∗,选择
x
=
ϵ
x=\epsilon
x=ϵ,
y
y
y选择第一个/前两个字符,
z
z
z选择剩下的
对于
w
=
a
k
(
b
∣
c
)
∗
k
≥
2
w=a^k\left(b|c\right)^*\ k\ge 2
w=ak(b∣c)∗ k≥2,选定
x
=
ϵ
,
y
=
a
a
x=\epsilon,y=aa
x=ϵ,y=aa,
z
z
z选择剩下的
即可满足pumping lemma
但是显然
{
a
b
n
c
n
∣
n
≥
1
}
∩
{
a
k
(
b
∣
c
)
∗
∣
k
≠
1
}
=
∅
\left\{ab^nc^n|n\ge1\right\}\cap\left\{a^k(b|c)^*|k\neq 1\right\}=\empty
{abncn∣n≥1}∩{ak(b∣c)∗∣k=1}=∅,
并且
{
a
b
n
c
n
∣
n
≥
1
}
\left\{ab^nc^n|n\ge1\right\}
{abncn∣n≥1}不是正则语言,所以
L
L
L不是正则语言

