LeetCode - 1703 得到连续 K 个 1 的最少相邻交换次数
目录
题目来源
1703. 得到连续 K 个 1 的最少相邻交换次数 - 力扣(LeetCode)
题目描述
给你一个整数数组 nums 和一个整数 k 。 nums 仅包含 0 和 1 。每一次移动,你可以选择 相邻 两个数字并将它们交换。
请你返回使 nums 中包含 k 个 连续 1 的 最少 交换次数。
示例
| 输入 | nums = [1,0,0,1,0,1], k = 2 |
| 输出 | 1 |
| 解释 | 在第一次操作时,nums 可以变成 [1,0,0,0,1,1] 得到连续两个 1 。 |
| 输入 | nums = [1,0,0,0,0,0,1,1], k = 3 |
| 输出 | 5 |
| 解释 | 通过 5 次操作,最左边的 1 可以移到右边直到 nums 变为 [0,0,0,0,0,1,1,1] 。 |
| 输入 | nums = [1,1,0,1], k = 2 |
| 输出 | 0 |
| 解释 | nums 已经有连续 2 个 1 了。 |
提示
1 <= nums.length <= 105nums[i]要么是0,要么是1。1 <= k <= sum(nums)
题目解析
本题和前面的
算法 - 最少交换次数来组合所有的1_伏城之外的博客-CSDN博客
题目类似,区别在于本题:“每一次移动,你可以选择 相邻 两个数字并将它们交换。”
而前面两题的交换是任意两个位置的数字可以直接交换。
因此本题的滑窗设计和前面略有不同。
比如
nums = [1,0,0,1,0,1], k = 2
如果才有下面这种滑窗设计,则是非常低效,不仅滑窗移动次数多,并且需要判断滑窗外部的1来到滑窗内部的最近距离
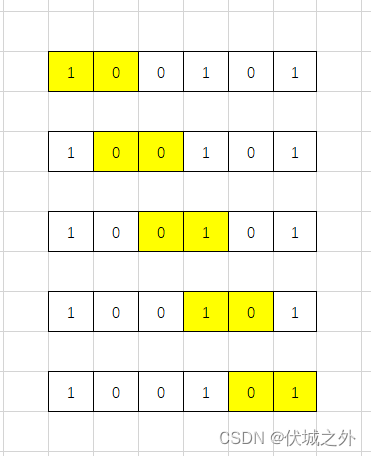
因此,我们不能采用上面滑窗设计。
题目要求,我们要让K个1组合到一起,我们可以直接让滑窗内含有K个1即可,如下
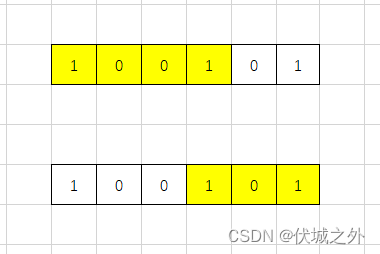
可以发现,此时滑窗情况大大减少,并且我们只需要关注滑窗内部K个1的移动即可,不需要关注滑窗外部的1。
但是此时滑窗的移动是非连续的,如上图,第一个滑窗起始位置是0,第二个滑窗起始位置直接跳到了3,但是我们可以换个角度看问题,第一个滑窗的起始位置是第一个1,第二个滑窗位置起始位置是第二个1,这样看的话,滑窗的移动就是连续的了。
因此我们需要统计输入数列中1的位置,将输入数列转为1位置数列,如下图所示
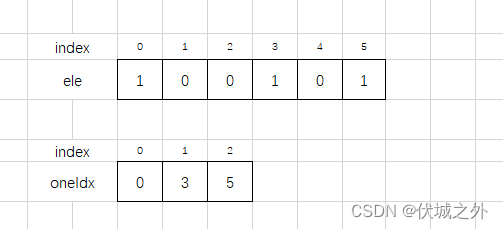
此时滑窗移动就可以转为下面连续情况
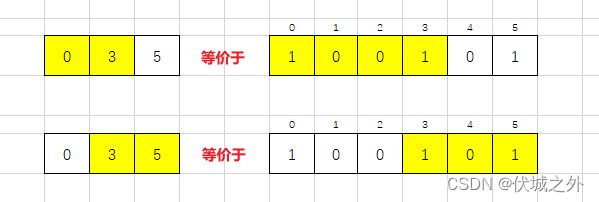
滑窗的移动问题解决后,我们就可以着手解决滑窗内部K个1组合到一起的问题,比如下面情况,

我们需要将索引0的一和索引3的一组合到一起,则可以让有两种方式:
- 将索引0的一交换到索引2的位置,即2-0,需要交换2次
- 将索引3的一交换到索引1的位置,即3-1,需要交换2次
上面两种方式是等价的。
我们将nums中1元素的索引选取出来定义为数组ones,

则当K=2时,每种滑窗情况需要交换:
- ones[1] - ones[0] 次
- ones[2] - ones[1] 次
- ....
- ones[ones.length - 1] - ones[ones.length - 2] 次
我们比较上面每种滑窗的交换次数,取最小值。
上面是K=2时的情况,算是特殊情况,下面我们看下K>2的情况,比如
输入数组nums = [0,1,0,0,1,1,0,1,0,1,1,1,1,0,1,0],K=7
则滑窗情况如下
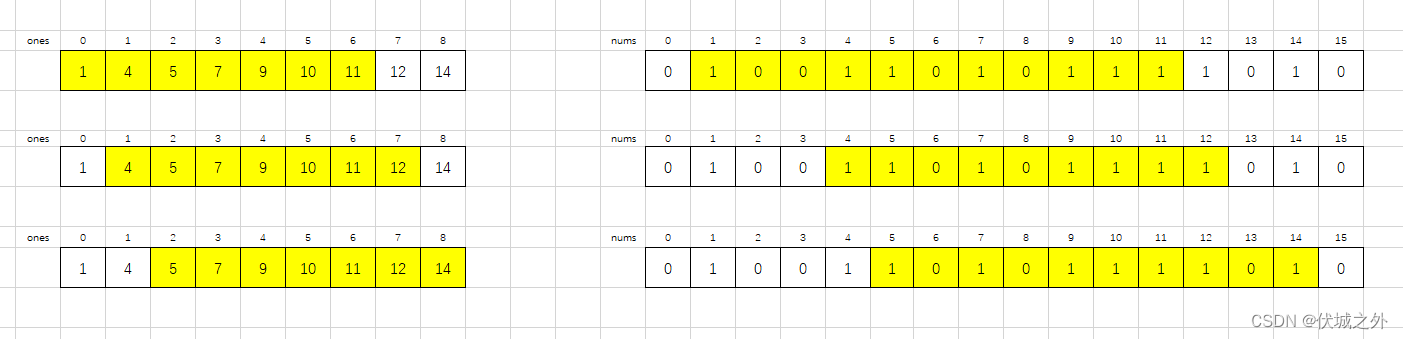
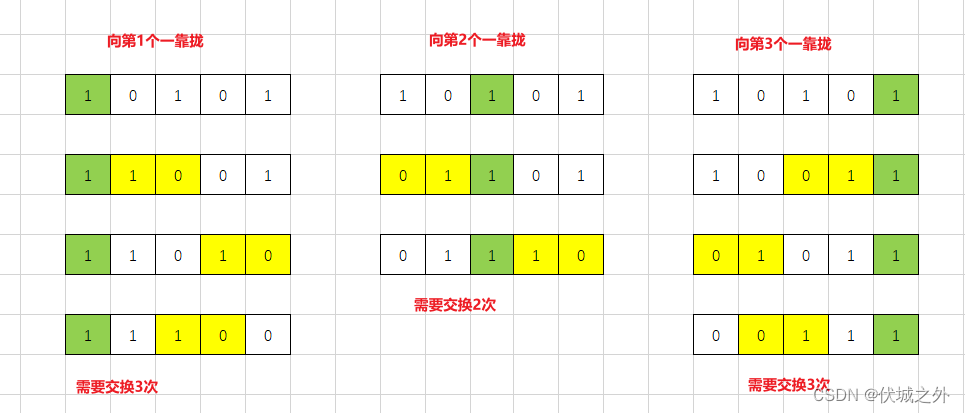
此时,我们会发现想要将7个1组合到一起,则情况非常多,比如第一种滑窗情况,我们可以选取一个1的位置,然后让剩余的1都往选取1的位置靠拢,那么就会有K种移动策略,我们要选取其中移动次数最少的那种策略。那么选取哪个位置的1的移动次数最少呢?
答案是中间位置的1。
我们通过下面例子来理解
可以发现,向中间位置的1靠拢所花费的交换次数是最少的。
因此我们需要求解出滑窗内,中间位置的1的索引,求解方程如下
i + Math.floor(k/2),
i 是滑窗中第一个1的索引位置(注意 i 取自ones数组,而不是nums数组),k就是滑窗内1的个数
公式最终结果也是ones数组的索引位置
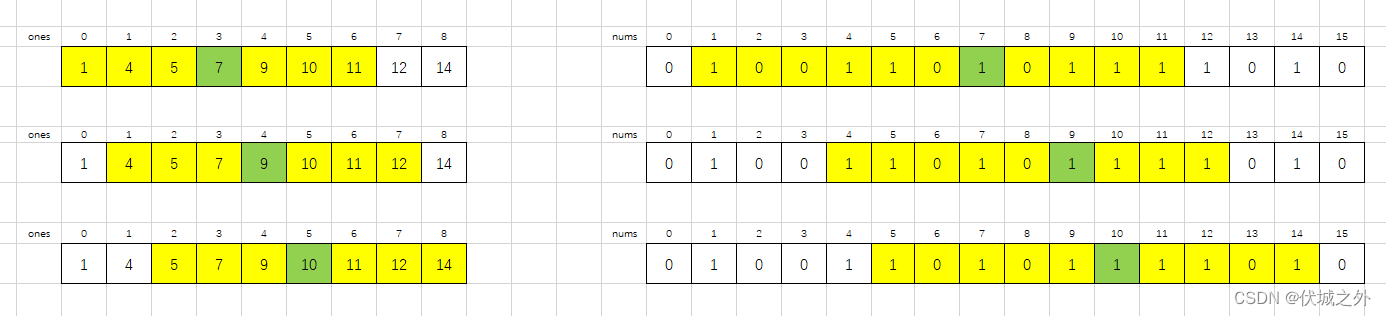
比如上面图示中,第一个滑窗情况中间位置的1的所有是:0 + Math.floor(7/2) = 3,即ones[3]就是滑窗内中间位置1的索引。
求得中间位置1后,我们就可以让两边的1往中间位置1靠拢,比如上面第一个滑窗情况,中间位置1的索引是7,而中间位置左边有3个1,右边有3个1,因此
我们需要预留索引4,5,6给左边的1,预留8,9,10索引给右边的1。
即如下图中,橙色部分就是预留位置

此时我们发现预留位置上已经有1了,因此我们判断如果预留位置有1的话,则跳过,但是这种方式会增加判断逻辑,让本就复杂的算法更加复杂。
实际上,我们有两种移动策略,让左边的1到预留位置

第一种,如上图,需要交换5次

第二种,如上图,需要交换5次
因此上面两种方式其实是等价的。但是第二种方式用代码实现起来更简单。
同理我们可以让中间位置1的右边1移动到预留位置

上面是基于nums的角度看的,我们再换一个视角用ones来看,红色数字就是预留位置
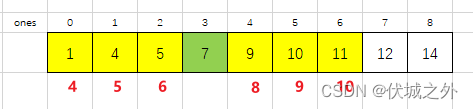
即让 左边的 索引5交换到6,4交换到5,1交换到4,交换次数一共是 (6-5) + (5-4) + (4-1) = 5
让 右边的 索引9交换到8,10交换到9,11交换到10 ,交换次数一共是 (9-8) + (10-9) + (11-10) = 3
因此,每一种滑窗都需花费O(K)的时间复杂度来计算最少交换次数。

而滑窗的情况有O(ones.length - K + 1),差不多是O(n)复杂度,因此计算所有滑窗情况种的最少交换次数需要O(n^2)复杂度,并不符合题目要求。
因此我们需要优化。
下面是起始位置在第1个一的滑窗和 起始位置在第2个一的滑窗,它们存在交集区域,如下红框
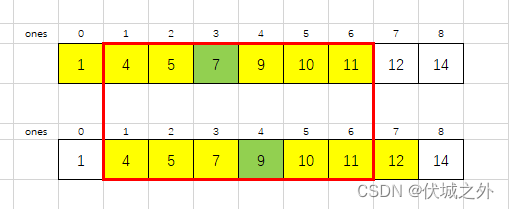
这两个交集区域是有关系的,它们其中元素相同,而中心位置不同,但是中心位置是相邻的
| 第一个滑窗 | 第二个滑窗 | |
| 4 | → 5 交换次数+1 | → 6 交换次数+2 |
| 5 | → 6 交换次数+1 | → 7 交换次数+2 |
| 7 | 中心位置,两边向我靠拢 | → 8 交换次数+1 |
| 9 | → 8 交换次数+1 | 中心位置,两边向我靠拢 |
| 10 | → 9 交换次数+1 | → 10 交换次数+0 |
| 11 | → 10 交换次数+1 | → 11 交换次数+0 |
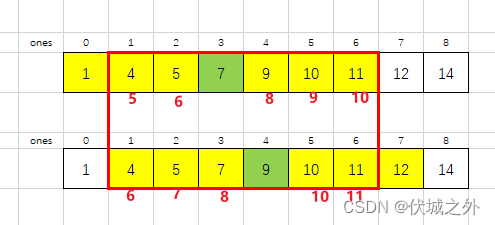
我们可以发现,中心位置从7变为9后,左边元素4,5的交换次数在原有基础上多加了一次,而这多出来的一次,其实就是上一次中心位置7 交换到 本次中心位置9 左边的8后,多出来的一次。
而右边元素10,11在原有基础上少了一次,二者少的一次,也是上一次中心位置7 交换到 本次中心位置9 左边的8后的影响导致的。
而无论是9到中心位置7的右边8,还是7到中心位置9的左边8的交换次数都是相同的。因此上面两个滑窗交集区域的交换次数差别,取决于7左边(不包含7)元素新增的交换次数,和9右边(不包含9)元素减少的交换次数 的 总和。
上面情况滑窗中元素个数刚好是奇数个,因此两个滑窗交集区域的7左边元素和9右边元素的个数是相同的,因此两个交集区域的交换次数是相等的。
如果滑窗中元素个数是偶数个,则此时导致两个滑窗的交集区域的交换次数不一致,如下例所示
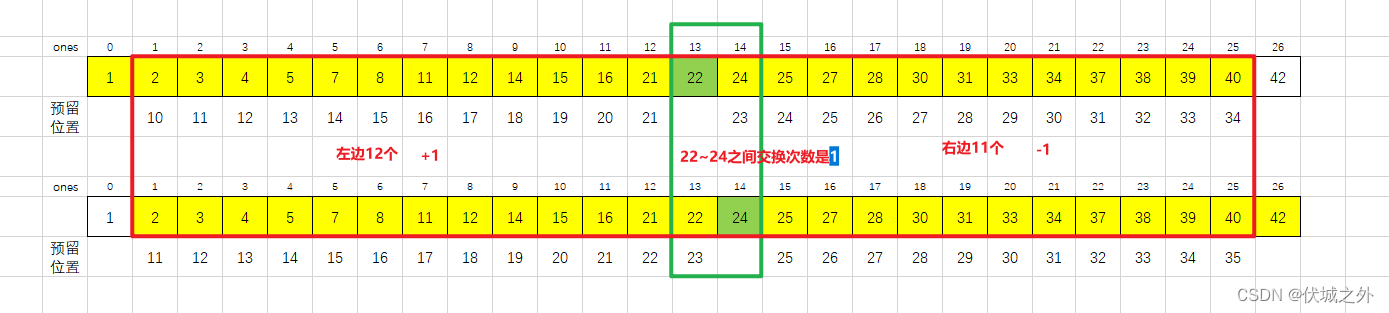
上面图示中,第二个滑窗的交集区域要比第一个滑窗的交集区域的交换次数 多1次 。
当我们知道了两次滑窗交集区域的交换次数 关系后,我们就可以避免重新计算每一个元素到中心位置的交换次数了,直接基于推导的关系计算出来即可。
而滑窗在向右移动一次后,就会失去一个元素,比如上图失去了ones[0],新增了ones[26]
因此,我们只需要在上一个滑窗的交换次数基础上,减去ones[0]到上一次的中心位置one[13]的交换次数,加上ones[26]到本次的中心位置ones[14]的交换次数,再加上两次滑窗交叉区域的差异交换次数,就是最终的题解。
算法源码
var minMoves = function (nums, k) {
// ones存储的是nums中1的索引位置
let ones = [];
nums.forEach((num, idx) => {
if (num === 1) ones.push(idx);
});
// 如果K=1, 即只要求1个1相连,则不需要交换
if (k === 1) {
return 0;
}
// 如果K=2,即要求2个1相连,则只需要分别计算
// ones[1] - 1 - ones[0], 第0个1 到 第1个1左边的位置的交换次数
// ones[2] - 1 - ones[1], 第1个1 到 第2个1左边的位置的交换次数
// ......
// ones[ones.len-1] - 1 - ones[ones.len - 2],
// 并求得以上所有结果中的最小值
else if (k === 2) {
let minSwapCount = ones[1] - 1 - ones[0];
for (let i = 2; i <= ones.length - 1; i++) {
minSwapCount = Math.min(minSwapCount, ones[i] - 1 - ones[i - 1]);
}
return minSwapCount;
}
// 如果K>2,即要求3个或3个以上1相连,则此时
else {
let minSwapCount = 0;
// 我们需要先求得中间位置的1的索引mid(ones数组)
let mid = Math.floor(k / 2);
// 再求出中间位置左边预留位置left(nums数组)
let left = ones[mid] - 1;
// 然后将位于中间位置左边的1依次交换到预留位置
for (let i = mid - 1; i >= 0; i--) {
minSwapCount += left - ones[i];
left--;
}
// 同理求出中间位置右边的预留位置right(nums数组)
let right = ones[mid] + 1;
// 然后将位于中间位置右边的1依次交换到预留位置
for (let i = mid + 1; i < k; i++) {
minSwapCount += ones[i] - right;
right++;
}
// ⬆ 以上得到的minSwapCount,就是第一个滑窗的交换次数
// 下面开始求解第一个滑窗之后的滑窗的交换次数,这里不再采用第一个滑窗的求解交换次数的方法,因为时间复杂度太大
let tmpSwapCount = minSwapCount;
// 第一个滑窗的起始位置是0(ones数组),则第二个滑窗的起始位置是1,最后一格滑窗的起始位置是ones.len - k
for (let i = 1; i <= ones.length - k; i++) {
// 本轮滑窗的中心位置curMid(ones数组)
let curMid = Math.floor(k / 2) + i;
// 上一轮滑窗的中心位置preMid(ones数组)
let preMid = curMid - 1;
// 计算两个中心位置间的交换次数
let midSwapCount = ones[curMid] - 1 - ones[preMid];
// 本轮和上一轮滑窗交集区域内,preMid左边的1个数
let leftOneCount = preMid - i;
// 本轮和上一轮滑窗交集区域内,curMid右边的1个数
let rightOneCount = i + k - 2 - curMid;
// 两轮滑窗交集区域交换次数的差异
let diff = (leftOneCount - rightOneCount) * midSwapCount;
// 本轮滑窗新增的1的索引位置
let curRight = i + k - 1;
// 本轮滑窗失去的1的所有位置
let preLeft = i - 1;
// 失去的1对应的交换次数
let minusCount = ones[preMid] - (preMid - preLeft) - ones[preLeft];
// 新增的1对应的交换次数
let addCount = ones[curRight] - (ones[curMid] + (curRight - curMid));
// 则本路滑窗的交换次数 = 上轮滑窗的交换次数 + diff - minusCount + addCount
tmpSwapCount = tmpSwapCount - minusCount + addCount + diff;
// 比较本轮和上轮的交换次数,只保留最小的
minSwapCount = Math.min(minSwapCount, tmpSwapCount);
}
return minSwapCount;
}
};