目录

1.函数作用

2.归一化的思想 

3.归一化的数学基础 

4.归一化Initializer::Normalize代码解读

4.1 构造函数

4.2 归一化的代码解读 

1.函数作用

        归一化特征点到同一尺度，作为后续normalize DLT的输入

2.归一化的思想 

        为什么要归一化？ Ah=0 矩阵A是利用8点法求基础矩阵的关键，所以Hartey就认为，利用8点法求基础矩阵不稳定的一个主要原因就是原始的图像像点坐标组成的系数矩阵A不好造成的，而造成A不好的原因是像点的齐次坐标各个分量的数量级相差太大。基于这个原因，Hartey提出一种改进的8点法，在应用8点法求基础矩阵之前，先对像点坐标进行归一化处理，即对原始的图像坐标做同向性变换，这样就可以减少噪声的干扰，大大的提高8点法的精度。

        预先对图像坐标进行归一化有以下好处： 能够提高运算结果的精度利用归一化处理后的图像坐标，对任何尺度缩放和原点的选择是不变的。        

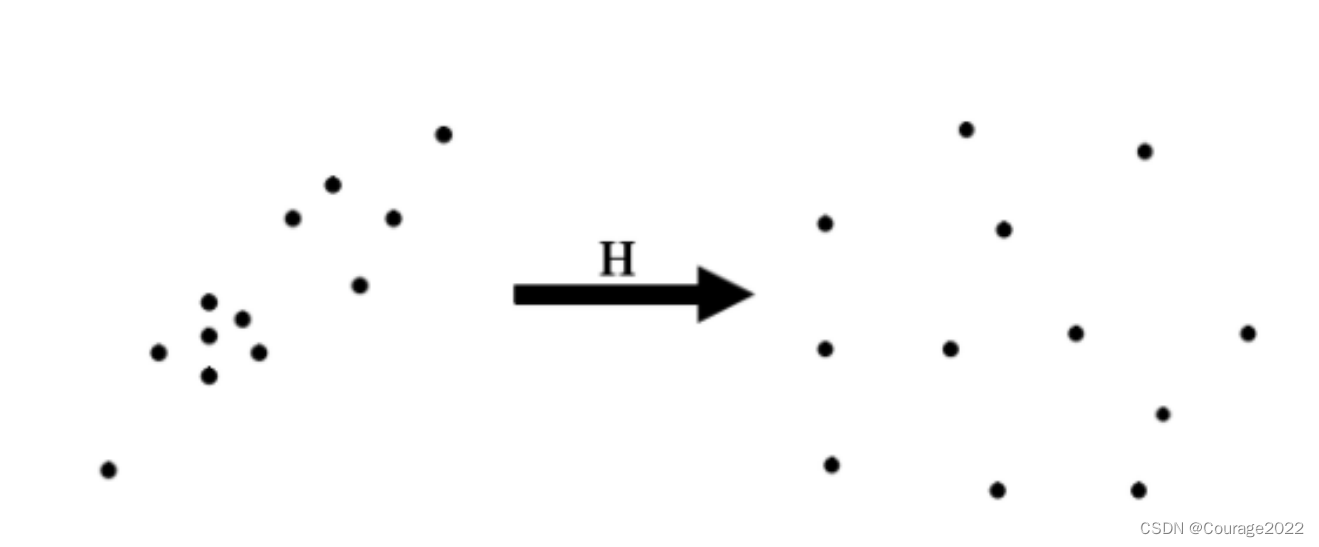
        归一化步骤预先为图像坐标选择了一个标准的坐标系中，消除了坐标变换对结果的影响。 归一化操作分两步进行，首先对每幅图像中的坐标进行平移（每幅图像的平移不同）使图像中匹配的点组成的点集的形心（Centroid）移动到原点；接着对坐标系进行缩放使得各个分量总体上有一样的平均值，各个坐标轴的缩放相同的。如下图所示：

         使用归一化的坐标虽然能够在一定程度上消除噪声、错误匹配带来的影响，但还是不够的。

3.归一化的数学基础 

        一阶矩就是随机变量的期望，二阶矩就是随机变量平方的期望；一阶绝对矩定义为变量与均值绝对值的平均。

4.归一化Initializer::Normalize代码解读

4.1 构造函数

 * @param[in] vKeys                               待归一化的特征点
 * @param[in & out] vNormalizedPoints             特征点归一化后的坐标
 * @param[in & out] T                             归一化特征点的变换矩阵

void Initializer::Normalize(const vector<cv::KeyPoint> &vKeys, vector<cv::Point2f> &vNormalizedPoints, cv::Mat &T)                           //将特征点归一化的矩阵

        我们输入参数为待归一化的特征点，输出参数为特征点归一化后的坐标与归一化变换矩阵。

4.2 归一化的代码解读 

void Initializer::Normalize(const vector<cv::KeyPoint> &vKeys, vector<cv::Point2f> &vNormalizedPoints, cv::Mat &T)                           //将特征点归一化的矩阵
{
    // 归一化的是这些点在x方向和在y方向上的一阶绝对矩（随机变量的期望）。

    // Step 1 计算特征点X,Y坐标的均值 meanX, meanY
    float meanX = 0;
    float meanY = 0;

	//获取特征点的数量
    const int N = vKeys.size();

	//设置用来存储归一后特征点的向量大小，和归一化前保持一致
    vNormalizedPoints.resize(N);

	//开始遍历所有的特征点
    for(int i=0; i<N; i++)
    {
		//分别累加特征点的X、Y坐标
        meanX += vKeys[i].pt.x;
        meanY += vKeys[i].pt.y;
    }

    //计算X、Y坐标的均值
    meanX = meanX/N;
    meanY = meanY/N;

    // Step 2 计算特征点X,Y坐标离均值的平均偏离程度 meanDevX, meanDevY，注意不是标准差
    float meanDevX = 0;
    float meanDevY = 0;

    // 将原始特征点减去均值坐标，使x坐标和y坐标均值分别为0
    for(int i=0; i<N; i++)
    {
        vNormalizedPoints[i].x = vKeys[i].pt.x - meanX;
        vNormalizedPoints[i].y = vKeys[i].pt.y - meanY;

		//累计这些特征点偏离横纵坐标均值的程度
        meanDevX += fabs(vNormalizedPoints[i].x);
        meanDevY += fabs(vNormalizedPoints[i].y);
    }

    // 求出平均到每个点上，其坐标偏离横纵坐标均值的程度；将其倒数作为一个尺度缩放因子
    meanDevX = meanDevX/N;
    meanDevY = meanDevY/N;
    float sX = 1.0/meanDevX;
    float sY = 1.0/meanDevY;

    // Step 3 将x坐标和y坐标分别进行尺度归一化，使得x坐标和y坐标的一阶绝对矩分别为1 
    // 这里所谓的一阶绝对矩其实就是随机变量到取值的中心的绝对值的平均值（期望）
    for(int i=0; i<N; i++)
    {
		//对，就是简单地对特征点的坐标进行进一步的缩放
        vNormalizedPoints[i].x = vNormalizedPoints[i].x * sX;
        vNormalizedPoints[i].y = vNormalizedPoints[i].y * sY;
    }

    // Step 4 计算归一化矩阵：其实就是前面做的操作用矩阵变换来表示而已
    // |sX  0  -meanx*sX|
    // |0   sY -meany*sY|
    // |0   0      1    |
    T = cv::Mat::eye(3,3,CV_32F);
    T.at<float>(0,0) = sX;
    T.at<float>(1,1) = sY;
    T.at<float>(0,2) = -meanX*sX;
    T.at<float>(1,2) = -meanY*sY;
}

        我们首先计算输入八点坐标的值和值的平均值meanX和meanY ，即

        计算每个特征点与值和值的平均值的偏差程度之和meanDevX和meanDevY，即

        计算meanDevX和meanDevY的倒数sX和sY，即

        用 SX 与 vNormalizedPoints[i].x 相乘为归一化的坐标，

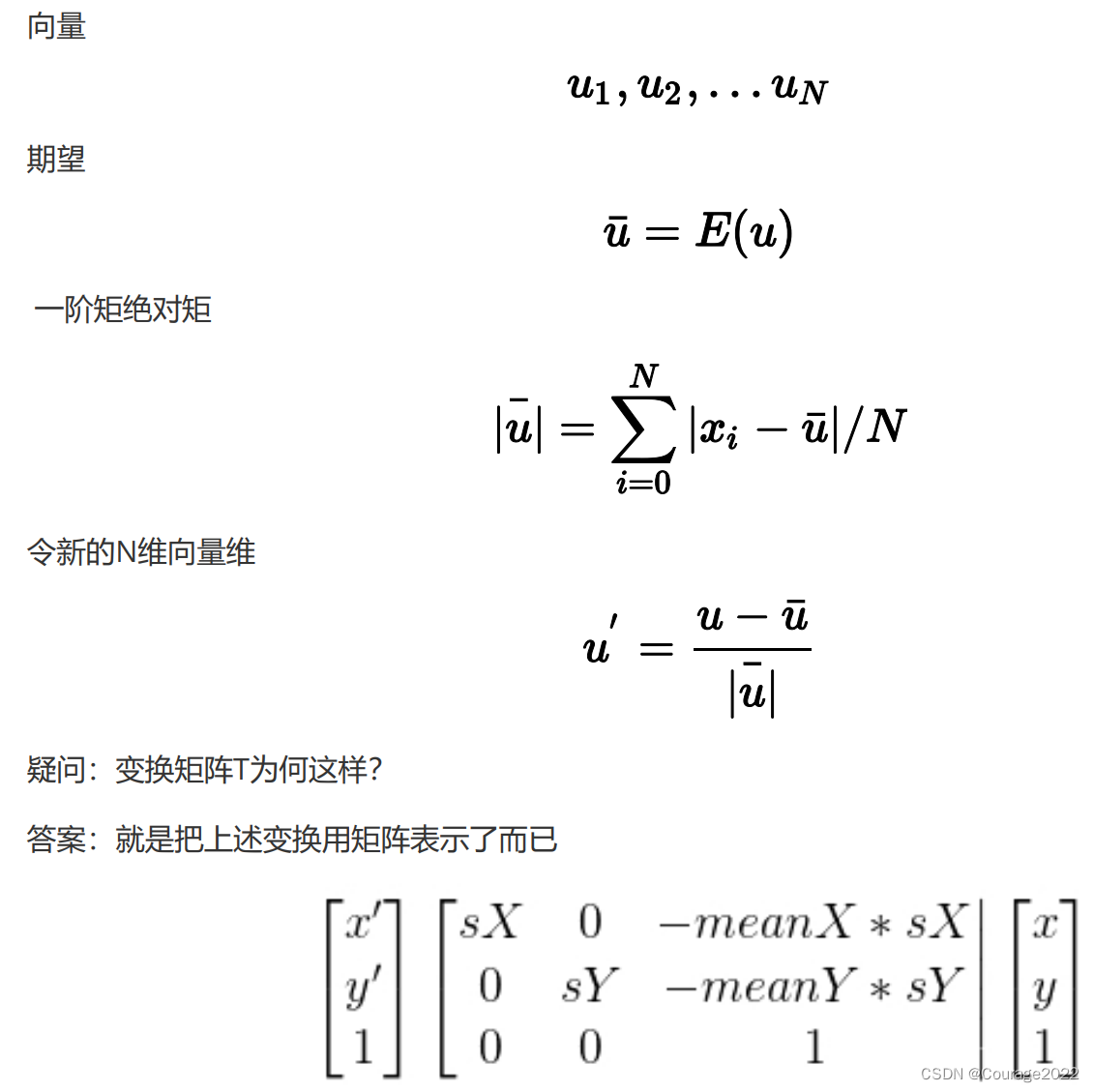
        变换矩阵可以表示为如上矩阵，即，矩阵为变换矩阵。