使用线段树解决数组任意区间元素修改问题
使用线段树解决数组任意区间元素修改问题
作者:Grey
原文地址:
要解决的问题
数组任意区间内的元素修改,增加,求和,时间复杂度都要达到 \(O(logN)\) 水平, 方法说明如下:
在数组 arr 中,L...R区间上的元素值都加上 V,如下方法
void add(L, R, V, arr)
在数组 arr 中,L...R区间上的元素值都更新成 V,如下方法
void update(L, R, V, arr)
在数组 arr 中,L...R区间上的元素求和并返回求和结果,如下方法
int query(L, R, arr)
注:L和R表示数组编号,通常数组的编号是从 0 开始,但是本文中涉及的线段树结构,人为规定,编号从1开始,0位置弃而不用。
之所以要弃而不用,是因为在进行线段树的下标换算的时候,可以用位运算来替代加减乘除运行,提高效率。
预处理
线段树要求数组长度必须是\(2^N\),如果不满足,则必须要对原始数组进行预处理,即通过在数组后面补 0 的方式将数组长度变成最近的一个满足\(2^N\)长度的数组,
接下来,将数组划分成一个个的区间,区间大小分别为:
1
2
4
8
……
\(2^N\)
例如:数组的长度为 8,我们将数组下标从 1 开始编号到 8,则按上述区间划分规则,可以得到一个满二叉树,如下图
1~8
/ \
1~4 5~8
/ \ / \
1~2 3~4 5~6 7~8
/ \ / \ / \ / \
1 2 3 4 5 6 7 8
如果数组长度不满足\(2^N\),要变成满二叉树,则需要通过补 0 的方式,比如数组只有 6 个元素,编号为1~6,其长度不满足 \(2^N\),那么 7 号位置和 8 号位置补 0,使数组长度满足\(2^3\)(即满足 \(2^N\) 长度)。然后再按上述过程构建满二叉树。满二叉树的节点覆盖了所有划分的区间数。
如果数组长度满足\(2^N\),则仅需要 \(2N\) 个区间就可以装下数组按规则划分的所有区间,如果不满足\(2^N\),则仅需要 \(4N\) 个区间就可以装下数组按规则划分的所有区间。
线段树这里的下标都用 1 开始,0 位置弃而不用 就是为了在任意位置(假设位置为i)有:
左孩子对应的下标是 \(2*i\) ,即:\(i<<1\);
右孩子对应的下标是 \(2*i+1\),即:\((i<<1)|1\)。
所以,假设原始数组为 origin, 长度为 \(N\) ,线段树需要将 origin 这个数组做如下预处理:
第一步,准备一个 \(N+1\) 长度的数组 arr ,arr 的 0 号位置弃而不用,从 1 号位置开始,arr 的 i 位置存原始数组 i-1 位置的值。
第二步,准备四个长度均为 \(4*(N+1)\) 的数组,每个数组的含义如下:
sum 数组
用来维护区间和
lazy 数组
用于累加和懒惰标记
change 数组
更新的值数组
update 数组
存放更新的慵懒标记
每个数组的用法后面会提到。
预处理部分的代码如下
public SegmentTree(int[] origin) {
final int n = origin.length + 1;
arr = new int[n];
// 0位置不用 从1位置开始使用
// 把 origin 的数组复制到 arr 数组中
// O(N)
System.arraycopy(origin, 0, arr, 1, origin.length);
final int range = n << 2;
sum = new int[range];
lazy = new int[range];
change = new int[range];
update = new boolean[range];
}
线段树初始化
完成预处理以后,线段树在初始化阶段,会把每个划分区间的累加和先计算出来,放入 sum 数组中,初始化代码和说明如下
// l...r 区间进行初始化
public void build(int l, int r, int i) {
if (l == r) {
// 区间l..r只有一个数,则这个数的值就是这个数所代表区间的累加和
sum[i] = arr[l];
return;
}
int mid = (l + r) >> 1;
build(l, mid, i << 1);
build(mid + 1, r, i << 1 | 1);
pushUp(i);
}
比如:arr[1...8] 这个数组,经过 build 操作后,会得到以下区间的累加和:
[1...8],[1...4],[5...8],[1...2],[3...4],[5...6],[7...8],[1...1],[2...2],[3...3],[4...4],[5...5],[6...6],[7...7],[8...8]
并保存在 sum 数组中。
private void pushUp(int rt) {
sum[rt] = sum[rt << 1] + sum[rt << 1 | 1];
}
pushUp方法很容易理解,即:每个区间的和等于它左右两个区间的和相加得到。前面提到,对于rt位置来说,左右孩子分别为rt << 1和rt << 1 | 1。所以sum[rt] = sum[rt << 1] + sum[rt << 1 | 1]。
例如:
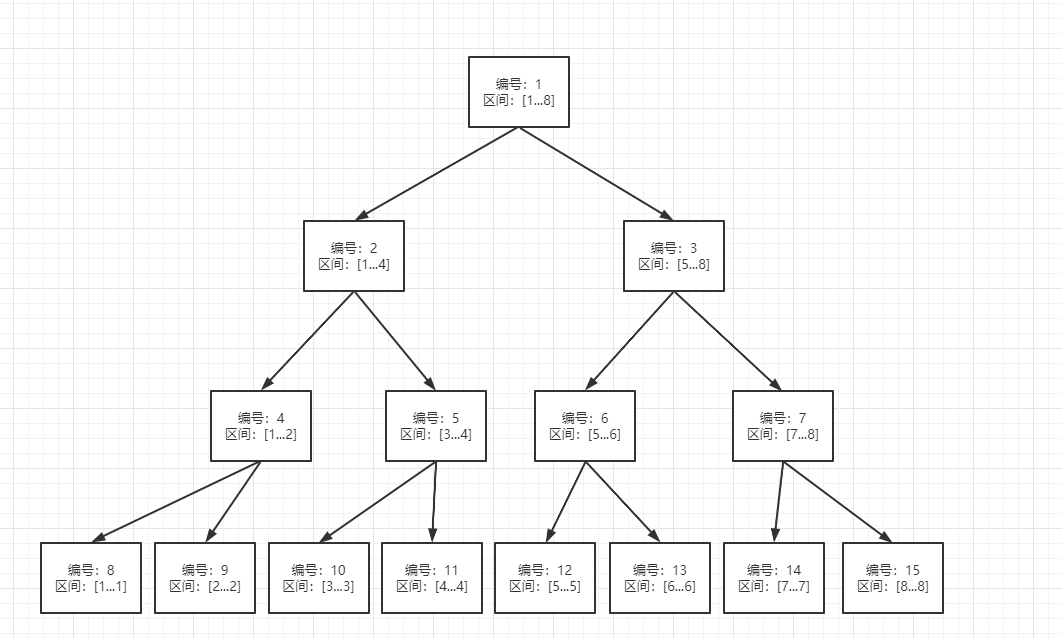
从上图中可以看出,当rt=5(上图中就是编号为 5 的格子所代表的区间)时,(rt << 1) = 10, (rt << 1 | 1) = 11,
sum[5] = sum[11] + sum[12]
即:编号5的区间的累加和等于编号10的累加和与编号11累加和再求和
再如:如上图,编号3的区间的累加和等于编号6和编号7的累加和再求累加。
其他位置同理。
build是递归方法,且满足master公式的计算条件,可以得到整个方法的复杂度为\(O(N)\),但也仅仅是在初始化的时候调用一次。
线段树后续的add,update,query方法都是 \(O(logN)\) 的复杂度。
区间内每个数都加一个值
即线段树的add方法,源码如下
public void add(int L, int R, int C, int l, int r, int rt) {
// 任务如果把此时的范围全包了!
if (L <= l && r <= R) {
sum[rt] += C * (r - l + 1);
lazy[rt] += C;
return;
}
int mid = (l + r) >> 1;
pushDown(rt, mid - l + 1, r - mid);
if (L <= mid) {
add(L, R, C, l, mid, rt << 1);
}
if (R > mid) {
add(L, R, C, mid + 1, r, rt << 1 | 1);
}
pushUp(rt);
}
注:L...R为任务区间, l...r是在数组在预处理的时候的划分区间
所以add方法表示:在L...R这个区间内的元素值,都加上一个 C 。
如果任务的范围把此时数组某个划分区间l...r包住了,则这个l...r这个区间范围内的值都要加上 C ,
即代码中 base case 的第一个逻辑
sum[rt] += C * (r - l + 1)
而
lazy[rt] += C
表示「加 C」这个任务hold在l...r区间内,不下发给子节点处理,这就是线段树的懒更新机制。
如果任务的范围无法把数组某个划分区间l...r包住,则l...r这个区间就要下发给左右子树进行处理。
但是在下发之前,要进行pushDown操作,在pushDown操作中,add方法会触发到的逻辑是:
private void pushDown(int rt, int ln, int rn) {
....
if (lazy[rt] != 0) {
lazy[rt << 1] += lazy[rt];
sum[rt << 1] += lazy[rt] * ln;
lazy[rt << 1 | 1] += lazy[rt];
sum[rt << 1 | 1] += lazy[rt] * rn;
lazy[rt] = 0;
}
....
}
这个操作表示:在l...r把任务下发到左右子树之前,先把l...r之前hold住的更新,即lazy[rt]中存的值,同步下发到左右子树进行更新,其中就包括两步:
第一步,左右子树都要加上之前父节点的lazy值,因为当时父节点在更新lazy的时候,是没有下发到左右子树的(懒更新),此时要下发了,
就必须把之前所有的lazy信息更新到左右子树,对应就是代码中的如下两行
lazy[rt << 1] += lazy[rt];
lazy[rt << 1 | 1] += lazy[rt];
第二步,左右子树的 sum 值,也会随着父节点的 lazy 值更新过来而整体更新,对应代码中如下两行
sum[rt << 1 | 1] += lazy[rt] * rn;
sum[rt << 1] += lazy[rt] * ln;
pushDown的这两个步骤时间复杂度 \(O(logN)\)。
此时,add方法在执行完pushDown操作后,就可以下发任务了,核心代码如下
if (L <= mid) {
add(L, R, C, l, mid, rt << 1);
}
if (R > mid) {
add(L, R, C, mid + 1, r, rt << 1 | 1);
}
pushUp(rt);
使用的类似二分的方式下发给左右两个孩子区间,主要判断依据是任务区间到底在左右子树的哪个子树范围内。
最后,执行pushUp方法,即把累加信息传递给父节点。
综上,线段树的add逻辑说明完毕。
区间内的值都更新为某个值
即线段树的update方法,update方法需要change数组和update数组配合。
public void update(int L, int R, int C, int l, int r, int rt) {
if (L <= l && r <= R) {
update[rt] = true;
change[rt] = C;
sum[rt] = C * (r - l + 1);
lazy[rt] = 0;
return;
}
// 当前任务躲不掉,无法懒更新,要往下发
int mid = (l + r) >> 1;
pushDown(rt, mid - l + 1, r - mid);
if (L <= mid) {
update(L, R, C, l, mid, rt << 1);
}
if (R > mid) {
update(L, R, C, mid + 1, r, rt << 1 | 1);
}
pushUp(rt);
}
base case的逻辑和add方法类似,如果任务范围包住了区间范围,则在区间内直接做更新,
update[rt] = true用于标识编号为rt的这个区间做了更新;
change[rt] = C;用于记录编号为rt的这个区间的值更新成了什么;
如果某个区间的值收到一个update方法,要求把这个区间内的值都更新为 C ,
这个 C 首先会被保存在change数组中,而且这个区间的所有lazy信息失效,
这个区间的sum值直接变成数据个数 * C,所以有如下逻辑。
sum[rt] = C * (r - l + 1);
lazy[rt] = 0;
如果任务包不住区间范围,和add类似,也需要下发,下发过程可以查看pushDown逻辑的如下分支:
private void pushDown(int rt, int ln, int rn) {
....
if (update[rt]) {
update[rt << 1] = true;
update[rt << 1 | 1] = true;
change[rt << 1] = change[rt];
change[rt << 1 | 1] = change[rt];
lazy[rt << 1] = 0;
lazy[rt << 1 | 1] = 0;
sum[rt << 1] = change[rt] * ln;
sum[rt << 1 | 1] = change[rt] * rn;
update[rt] = false;
}
....
}
下发过程中,左右子树的更新标志位都需要设置为 true, 且左右子树区间需要更新的值均为父区间需要更新的值,即:
update[rt << 1] = true;
update[rt << 1 | 1] = true;
change[rt << 1] = change[rt];
change[rt << 1 | 1] = change[rt];
由于区间需要更新,所以lazy失效,设置为0,sum可以直接通过公式:数组区间元素个数*更新值计算出来。
任务下发后,和add方法一样,判断更新的区间在哪个子树范围,递归调用update执行更新操作即可,
最后更新完毕后,需要把更新后的左右子树之和信息传给父节点的sum信息中。
综上,线段树的update方法说明完毕。
返回区间之和
求区间之和的方法query和之前的add,update方法类似,
public long query(int L, int R, int l, int r, int rt) {
if (L <= l && r <= R) {
return sum[rt];
}
int mid = (l + r) >> 1;
pushDown(rt, mid - l + 1, r - mid);
long ans = 0;
if (L <= mid) {
ans += query(L, R, l, mid, rt << 1);
}
if (R > mid) {
ans += query(L, R, mid + 1, r, rt << 1 | 1);
}
return ans;
}
需要注意:求和之前,如果任务范围没包住区间范围,要执行一次pushDown操作,才能把各个相关区间的信息最后整合出来。
线段树的适用场景
父节点如果可以通过左右简单加工得到,就可以用线段树
什么时候不能用线段树呢?
比如:
要求数组某个区间出现次数最多的值
这个就无法用线段树,因为出现次数最多的值可以既不是左边出现最多的值,也不是右边出现最多的值
线段树完整源码(含对数器)
public class Code_SegmentTree {
public static class SegmentTree {
// 原序列的信息从0开始,但在arr里是从1开始的
private int[] arr;
// 维护区间和
private int[] sum;
// lazy[]为累加和懒惰标记
private int[] lazy;
// change[]为更新的值
private int[] change;
// update[]为更新慵懒标记
private boolean[] update;
public SegmentTree(int[] origin) {
final int n = origin.length + 1;
arr = new int[n];
// 0位置不用 从1位置开始使用
System.arraycopy(origin, 0, arr, 1, origin.length);
final int range = n << 2;
sum = new int[range];
lazy = new int[range];
change = new int[range];
update = new boolean[range];
}
// 在初始化阶段调用 O(N)
public void build(int l, int r, int i) {
if (l == r) {
sum[i] = arr[l];
return;
}
int mid = (l + r) >> 1;
build(l, mid, i << 1);
build(mid + 1, r, i << 1 | 1);
pushUp(i);
}
private void pushUp(int rt) {
sum[rt] = sum[rt << 1] + sum[rt << 1 | 1];
}
// 之前的,所有懒增加,和懒更新,从父范围,发给左右两个子范围
// 分发策略是什么
// ln表示左子树元素结点个数,rn表示右子树结点个数
private void pushDown(int rt, int ln, int rn) {
if (update[rt]) {
update[rt << 1] = true;
update[rt << 1 | 1] = true;
change[rt << 1] = change[rt];
change[rt << 1 | 1] = change[rt];
lazy[rt << 1] = 0;
lazy[rt << 1 | 1] = 0;
sum[rt << 1] = change[rt] * ln;
sum[rt << 1 | 1] = change[rt] * rn;
update[rt] = false;
}
if (lazy[rt] != 0) {
lazy[rt << 1] += lazy[rt];
sum[rt << 1] += lazy[rt] * ln;
lazy[rt << 1 | 1] += lazy[rt];
sum[rt << 1 | 1] += lazy[rt] * rn;
lazy[rt] = 0;
}
}
// L~R 所有的值变成C
public void update(int L, int R, int C, int l, int r, int rt) {
if (L <= l && r <= R) {
update[rt] = true;
change[rt] = C;
sum[rt] = C * (r - l + 1);
lazy[rt] = 0;
return;
}
int mid = (l + r) >> 1;
pushDown(rt, mid - l + 1, r - mid);
if (L <= mid) {
update(L, R, C, l, mid, rt << 1);
}
if (R > mid) {
update(L, R, C, mid + 1, r, rt << 1 | 1);
}
pushUp(rt);
}
// L...R是任务区间,在这个区间范围内都加C
public void add(int L, int R, int C, int l, int r, int rt) {
if (L <= l && r <= R) {
sum[rt] += C * (r - l + 1);
lazy[rt] += C;
return;
}
int mid = (l + r) >> 1;
pushDown(rt, mid - l + 1, r - mid);
if (L <= mid) {
add(L, R, C, l, mid, rt << 1);
}
if (R > mid) {
add(L, R, C, mid + 1, r, rt << 1 | 1);
}
pushUp(rt);
}
// 1~6 累加和是多少? 1~8 rt
public long query(int L, int R, int l, int r, int rt) {
if (L <= l && r <= R) {
return sum[rt];
}
int mid = (l + r) >> 1;
pushDown(rt, mid - l + 1, r - mid);
long ans = 0;
if (L <= mid) {
ans += query(L, R, l, mid, rt << 1);
}
if (R > mid) {
ans += query(L, R, mid + 1, r, rt << 1 | 1);
}
return ans;
}
}
public static class Right {
public int[] arr;
public Right(int[] origin) {
arr = new int[origin.length + 1];
System.arraycopy(origin, 0, arr, 1, origin.length);
}
public void update(int L, int R, int C) {
for (int i = L; i <= R; i++) {
arr[i] = C;
}
}
public void add(int L, int R, int C) {
for (int i = L; i <= R; i++) {
arr[i] += C;
}
}
public long query(int L, int R) {
long ans = 0;
for (int i = L; i <= R; i++) {
ans += arr[i];
}
return ans;
}
}
public static int[] genarateRandomArray(int len, int max) {
int size = (int) (Math.random() * len) + 1;
int[] origin = new int[size];
for (int i = 0; i < size; i++) {
origin[i] = (int) (Math.random() * max) - (int) (Math.random() * max);
}
return origin;
}
public static boolean test() {
int len = 100;
int max = 1000;
int testTimes = 50000;
int addOrUpdateTimes = 1000;
int queryTimes = 500;
for (int i = 0; i < testTimes; i++) {
int[] origin = genarateRandomArray(len, max);
SegmentTree seg = new SegmentTree(origin);
int S = 1;
int N = origin.length;
int root = 1;
seg.build(S, N, root);
Right rig = new Right(origin);
for (int j = 0; j < addOrUpdateTimes; j++) {
int num1 = (int) (Math.random() * N) + 1;
int num2 = (int) (Math.random() * N) + 1;
int L = Math.min(num1, num2);
int R = Math.max(num1, num2);
int C = (int) (Math.random() * max) - (int) (Math.random() * max);
if (Math.random() < 0.5) {
seg.add(L, R, C, S, N, root);
rig.add(L, R, C);
} else {
seg.update(L, R, C, S, N, root);
rig.update(L, R, C);
}
}
for (int k = 0; k < queryTimes; k++) {
int num1 = (int) (Math.random() * N) + 1;
int num2 = (int) (Math.random() * N) + 1;
int L = Math.min(num1, num2);
int R = Math.max(num1, num2);
long ans1 = seg.query(L, R, S, N, root);
long ans2 = rig.query(L, R);
if (ans1 != ans2) {
return false;
}
}
}
return true;
}
public static void main(String[] args) {
int[] origin = {2, 1, 1, 2, 3, 4, 5};
SegmentTree seg = new SegmentTree(origin);
int S = 1; // 整个区间的开始位置,规定从1开始,不从0开始 -> 固定
int N = origin.length; // 整个区间的结束位置,规定能到N,不是N-1 -> 固定
int root = 1; // 整棵树的头节点位置,规定是1,不是0 -> 固定
int L = 2; // 操作区间的开始位置 -> 可变
int R = 5; // 操作区间的结束位置 -> 可变
int C = 4; // 要加的数字或者要更新的数字 -> 可变
// 区间生成,必须在[S,N]整个范围上build
seg.build(S, N, root);
// 区间修改,可以改变L、R和C的值,其他值不可改变
seg.add(L, R, C, S, N, root);
// 区间更新,可以改变L、R和C的值,其他值不可改变
seg.update(L, R, C, S, N, root);
// 区间查询,可以改变L和R的值,其他值不可改变
long sum = seg.query(L, R, S, N, root);
System.out.println(sum);
System.out.println("对数器测试开始...");
System.out.println("测试结果 : " + (test() ? "通过" : "未通过"));
}
}
LeetCode 上可参考如下题目
LeetCode 307. Range Sum Query - Mutable
更多
参考资料
相关文章
- Java面试题总结
- 记一次 .NET 某桌面奇侠游戏 非托管内存泄漏分析
- 2021 VDC :vivo 互联网服务亿级用户的技术架构演进之路
- vivo浏览器的快速开发平台实践-总览篇
- 字节码引用检测原理与实战
- vivo 敏感词匹配系统的设计与实践
- Redis线程模型的前世今生
- 服务API版本控制设计与实践
- Chrome 插件特性及实战场景案例分析
- vivo统一告警平台设计与实践
- 如何“拼”出一个页面-游戏中心模块化实践
- 深入剖析 RocketMQ 源码 - 消息存储模块
- vivo 全球商城:商品系统架构设计与实践
- 深入剖析Redis客户端Jedis的特性和原理
- 高并发场景下JVM调优实践之路
- 你分库分表的姿势对么?——详谈水平分库分表
- 高效动画实现原理-Jetpack Compose 初探索
- Redis大集群扩容性能优化实践
- 深入剖析 Spring WebFlux
- 设计模式如何提升 vivo 营销自动化业务扩展性 | 引擎篇01

