1 基本的定义

　　正定和半正定这两个词的英文分别是 positive definite 和 positive semi-definite，其中，definite是一个形容词，表示“明确的、确定的”等意思。

　　定义1：给定一个大小为  $n \times n$  的实对称矩阵  $A$ ，若对于任意长度为  $n$  的非零向量  $\boldsymbol{x}$  有 $ \boldsymbol{x}^{T} A \boldsymbol{x}>0$  恒成立， 则矩阵  $A$  是一个正定矩阵。

　　正定矩阵：对于 $n$ 阶实对称矩阵 $A$ ，下列条件是等价的：

1. $A$ 是正定矩阵；
2. $A$ 的一切顺序主子式均为正；
3. $A$ 的一切主子式均为正；
4. $A$ 的特征值均为正；
5. 存在实可逆矩阵 $C$，使 $A=C′C$；
6. 存在秩为 $n$ 的 $m×n$ 实矩阵 B，使 $A=B′B$；
7. 存在主对角线元素全为正的实三角矩阵 $R$，使 $A=R′R$  。

例1：单位矩阵 $I \in \mathbb{R}^{2 \times 2}$ 是否是正定矩阵?
　　解：设向量 $ \boldsymbol{x}=\left[\begin{array}{l}x_{1} \\ x_{2}\end{array}\right] \in \mathbb{R}^{2}$ 为非零向量， 则

　　　　$\boldsymbol{x}^{T} \boldsymbol{I} \boldsymbol{x}=\boldsymbol{x}^{T} \boldsymbol{x}=x_{1}^{2}+x_{2}^{2}$

　　由于 $ \boldsymbol{x} \neq \mathbf{0} $，故$ \boldsymbol{x}^{T} I \boldsymbol{x}>0$ 恒成立，即单位矩阵 $ I \in \mathbb{R}^{2 \times 2}$ 是正定矩阵。

扩展：对于任意单位矩阵 $I \in \mathbb{R}^{n \times n}$ 而言，给定任意非零向量 $\boldsymbol{x} \in \mathbb{R}^{n}$ ， 恒有

　　　　$\begin{array}{l} \boldsymbol{x}^{T} I \boldsymbol{x}=\boldsymbol{x}^{T} \boldsymbol{x} \\ =x_{1}^{2}+x_{2}^{2}+\cdots+x_{n}^{2}>0 \end{array}$

例2：实对称矩阵 $A=\left[\begin{array}{ccc}2 & -1 & 0 \\ -1 & 2 & -1 \\ 0 & -1 & 2\end{array}\right] \in \mathbb{R}^{3 \times 3} $ 是否是正定矩阵? 　　

　　解：设向量 $\boldsymbol{x}=\left[\begin{array}{l}x_{1} \\ x_{2} \\ x_{3}\end{array}\right] \in \mathbb{R}^{3}$ 为非零向量，则

　　　　$\begin{array}{l} \boldsymbol{x}^{T} A \boldsymbol{x}=\left[\begin{array}{ll} \left(2 x_{1}-x_{2}\right) & \left(-x_{1}+2 x_{2}-x_{3}\right) & -x_{2}+2 x_{3} \end{array}\right]\left[\begin{array}{l} x_{1} \\ x_{2} \\ x_{3} \end{array}\right]  \end{array}$　

　　　　$ =x_{1}^{2}+\left(x_{1}-x_{2}\right)^{2}+\left(x_{2}-x_{3}\right)^{2}+x_{3}^{2}>0$

　　因此，矩阵 A 是正定矩阵。

　　定义2：给定一个大小为  $n \times n$  的实对称矩阵  $A$ ，  若对于任意长度为  $n$  的向量  $\boldsymbol{x} $， 有  $\boldsymbol{x}^{T} A \boldsymbol{x} \geq 0$  恒成立，则矩阵  $A $ 是一个半正定矩阵。

　　半正定矩阵：设 A 是 n 阶实对称矩阵，则下列的条件等价：

　　1.$A$ 是半正定的。

　　2.$A$ 的所有主子式均为非负的。

　　3.$A$ 的特征值均为非负的。

　　4.存在 $n$ 阶实矩阵 $C$，使 $A=C′C$.

　　5.存在秩为 $r$ 的 $r×n$ 实矩阵 $B$，使 $A=B′B$.

　　根据正定矩阵和半正定矩阵的定义，我们也会发现：半正定矩阵包括了正定矩阵

2 从二次函数到正定/半正定矩阵

　　我们学习过二次函数 $y=a x^{2}$ ， 该函数的曲线会经过坐标原点，当参数 $a>0$ 时，曲线的 “开口" 向上，参数 $a<0$ 时，曲线的 "开口" 向下。
　　以 y=2 x^{2} 为例, 曲线如下:

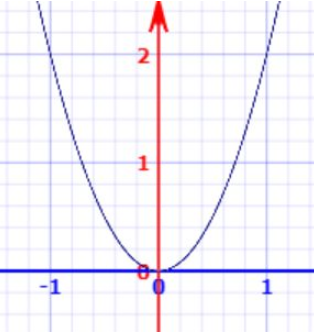
　　实际上，我们可以将 $y=\boldsymbol{x}^{T} A \boldsymbol{x}$ 视作 $y=a x^{2}$ 的多维表达式。
　　当我们希望 $ y=\boldsymbol{x}^{T} A \boldsymbol{x} \geq 0$ 对于任意向量 $ \boldsymbol{x}$ 都恒成立，就要求矩阵 $ A$ 是一个半正定矩阵，对应于二次函数， $ y=a x^{2}>0$，$ \forall x $  需要使得 $ a \geq 0 $。
　　另外，在 $ y=a x^{2}$ 中，我们还知道：若 $ a>0$ ，则对于任意 $ x \neq 0$， 有 $ y>0$ 恒成立。 这在 $ y=\boldsymbol{x}^{T} A \boldsymbol{x}$ 也有契合之处，当矩阵 $ A$ 是正定矩阵时，对于任意 $\boldsymbol{x} \neq \mathbf{0}, \quad y>0$ 恒成 立。

3 正定矩阵和半正定矩阵的直观解释

 若给定任意一个正定矩阵  $A \in \mathbb{R}^{n \times n}$  和一个非零向量  $\boldsymbol{x} \in \mathbb{R}^{n}$，则两者相乘得到的向量 $ \boldsymbol{y}=A \boldsymbol{x} \in \mathbb{R}^{n}$  与向量  $\boldsymbol{x}$  的夹角恒小于  $\frac{\pi}{2} $。 (等价于:  $\boldsymbol{x}^{T} A \boldsymbol{x}>0$。)

例3：给定向量 $\boldsymbol{x}=\left[\begin{array}{l}2 \\ 1\end{array}\right] \in \mathbb{R}^{2}$， 对于单位矩阵 $I=\left[\begin{array}{ll}1 & 0 \\ 0 & 1\end{array}\right] \in \mathbb{R}^{2 \times 2} $， 则

　　　　$\boldsymbol{y}=I \boldsymbol{x}=\boldsymbol{x}=\left[\begin{array}{l} 2 \\1 \end{array}\right]$

　　向量 $ \boldsymbol{x}, \boldsymbol{y} \in \mathbb{R}^{2}$ 之间的夹角为

　　　　$\begin{array}{l} \cos \langle\boldsymbol{x}, \boldsymbol{y}\rangle=\frac{\boldsymbol{x}^{T} \boldsymbol{y}}{\|\boldsymbol{x}\| \cdot\|\boldsymbol{y}\|} \\ =\frac{2 \times 2+1 \times 1}{\sqrt{2^{2}+1^{2}} \cdot \sqrt{2^{2}+1^{2}}} \\ =1 \end{array}$

　　即两个向量之间的夹角为 $0^{\circ}$。

若给定任意一个半正定矩阵  $A \in \mathbb{R}^{n \times n}$  和一个向量  $\boldsymbol{x} \in \mathbb{R}^{n} $，  则两者相乘得到的向量  $\boldsymbol{y}=A \boldsymbol{x} \in \mathbb{R}^{n}$  与向量  $\boldsymbol{x}$  的夹角恒小于或等于  $\frac{\pi}{2}$ .  (等价于:  $\boldsymbol{x}^{T} A \boldsymbol{x} \geq 0$) 

例4：给定向量 $\boldsymbol{x}=\left[\begin{array}{l}1 \\ 2 \\ 1\end{array}\right] \in \mathbb{R}^{3}$，对于实对称矩阵 $A=\left[\begin{array}{ccc}2 & -1 & 0 \\ -1 & 2 & -1 \\ 0 & -1 & 2\end{array}\right] \in \mathbb{R}^{3 \times 3} $ ，则

　　　　$\boldsymbol{y}=A \boldsymbol{x}=\left[\begin{array}{l} 0 \\ 2 \\ 0 \end{array}\right]$

　　向量 $ \boldsymbol{x}, \boldsymbol{y} \in \mathbb{R}^{2}$ 之间的夹角为

　　　　$\cos \langle\boldsymbol{x}, \boldsymbol{y}\rangle=\frac{\boldsymbol{x}^{T} \boldsymbol{y}}{\|\boldsymbol{x}\| \cdot\|\boldsymbol{y}\|}=\frac{\sqrt{6}}{3}$

$