提供了编程的基础技术教程

zl程序教程

您现在的位置是：首页 >  其他

当前栏目

【快速幂】斐波那契数列

2023-03-14 09:45:14 时间

快速幂运算：

　　快速幂的目的就是做到快速求幂，假设我们要求a^b,按照朴素算法就是把a连乘b次，这样一来时间复杂度是O(b)也即是O(n)级别，快速幂能做到O(logn)，快了好多好多。它的原理如下：

　　假设我们要求a^b，那么其实b是可以拆成二进制的，该二进制数第i位的权为2^(i-1)，例如当b==11时：

　　　　 a11=a(2^0+2^1+2^3)

　　11的二进制是1011，11 = 2³×1 + 2²×0 + 2¹×1 + 2º×1，因此，我们将a¹¹转化为算式 a2^0*a2^1*a2^3，也就是a1*a2*a8 ，看出来快的多了吧原来算11次，现在算三次，其中a1  a2  a8的计算方式代码注释里面写着。

　　代码：

 1 public class NExponent {
 2 
 3     public static void main(String[] args) {
 4         System.out.println(ex2(2, 3));
 5     }
 6     
 7     public static int ex(int a,int n){
 8         if(n==0)return 1;
 9         if(n==1)return a;
10         int temp = a; // a的1次方
11         int res = 1;
12         int exponent = 1;
13         while((exponent<<1)<n){
14             temp = temp * temp;
15             exponent = exponent << 1;
16         }
17         res *= ex(a,n-exponent);
18         return res * temp;
19     }
20     
21     /**
22      * 快速幂  O(lgn)
23      */
24     public static long ex2(long n,long m){
25         if(n==0) return 1;
26         long pingFangShu = n; // n 的 1 次方
27         long result = 1;
28         while (m != 0) {
29             // 遇1累乘现在的幂
30             if ((m & 1) == 1)
31                 result *= pingFangShu;
32             // 每移位一次，幂累乘方一次
33             pingFangShu = pingFangShu * pingFangShu;
34             // 右移一位
35             m >>= 1;
36         }
37         return result;
38     }
39 }

题目：矩阵快速幂求解斐波那契数列

　　

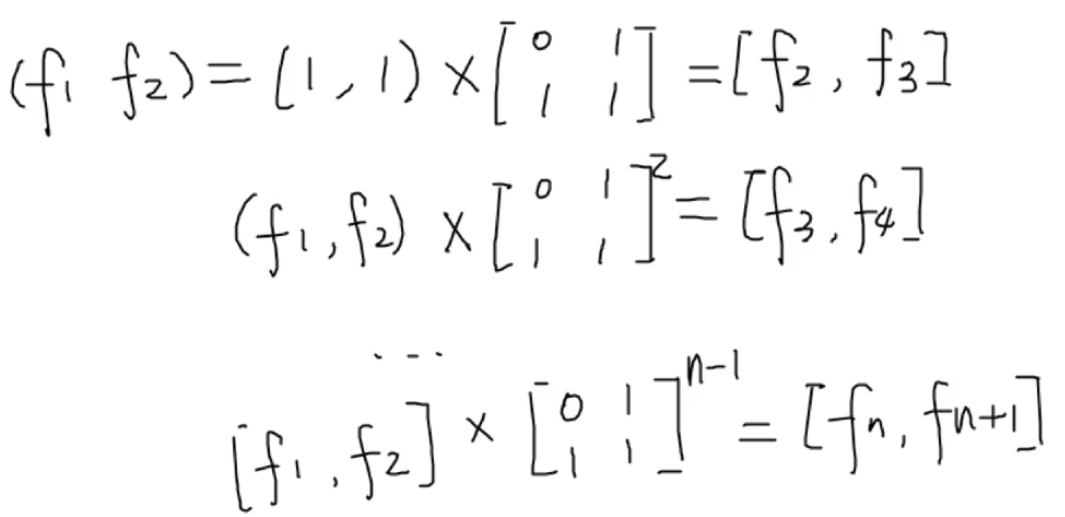
　　代码：

 1 public class Fib {
 2 
 3     public static void main(String[] args) {
 4         for (int i = 1; i < 10; i++) {
 5             System.out.print(fib(i)+" ");
 6         }
 7     }
 8     
 9     // 矩阵运算求解斐波那契数列
10     static long fib(long n){
11         if (n == 1 || n == 2) return 1;
12         long[][] matrix = { 
13                 { 0, 1 }, 
14                 { 1, 1 } 
15                 };
16         long[][] res = matrixPower(matrix, n - 1);// 乘方
17         res = matrixMultiply(new long[][] { { 1, 1 } }, res);// 矩阵相乘
18         return res[0][0];
19     }
20     
21     public static long[][] matrixPower(long[][] matrix, long p) {
22         // 初始化结果为单位矩阵，对角线为1
23         long[][] result = new long[matrix.length][matrix[0].length];
24         // 单位矩阵，相当于整数的1
25         for (int i = 0; i < result.length; i++) {
26             result[i][i] = 1;
27         }
28 
29         // 平方数
30         long[][] pingFang = matrix; // 一次方
31         while (p != 0) {
32             if ((p & 1) != 0) { // 当前二进制位最低位为1，将当前平方数乘到结果中
33                 result = matrixMultiply(result, pingFang);//
34             }
35             // 平方数继续上翻
36             pingFang = matrixMultiply(pingFang, pingFang);
37             p >>= 1;
38         }
39         return result;
40     }
41     
42     /**
43      * 矩阵乘法 矩阵1为n*m矩阵，矩阵2为m*p矩阵 结果为n*p矩阵
44      */
45     public static long[][] matrixMultiply(long[][] m1, long[][] m2) {
46         final int n = m1.length;
47         final int m = m1[0].length;
48         if (m != m2.length)
49             throw new IllegalArgumentException();
50         final int p = m2[0].length;
51 
52         long[][] result = new long[n][p];// 新矩阵的行数为m1的行数，列数为m2的列数
53 
54         for (int i = 0; i < n; i++) {// m1的每一行
55             for (int j = 0; j < p; j++) {// m2的每一列
56                 for (int k = 0; k < m; k++) {
57                     result[i][j] += m1[i][k] * m2[k][j];
58                 }
59             }
60         }
61         return result;
62     }
63 
64 }

　　结果：

　　　　

 

相关文章