「数学」平面分割

本题为3月14日23上半学期集训每日一题中A题的题解

题面

题目描述

同一平面内有n（ (n leq 500) ）条直线，已知其中p（ (p geq 2) ）条直线相交于同一点，则这n条直线最多能将平面分割成多少个不同的区域？

输入

两个整数n（ (n leq 500) ）和p（如果 (ngeq 2) 则 (2leq p leq n) ）。

输出

一个正整数，代表最多分割成的区域数目。

样例输入

12  5

样例输出

73

思路分析

如果你还有少许高中或初中数学知识的记忆的话,应该知道直线分割平面的数量是有规律的.这里我们通过观察法来找找规律.

相交于同一点

先来看看相交于同一点的几条直线能把平面分成多少个部分.

当只有一条直线时,平面会被它分成两个部分:

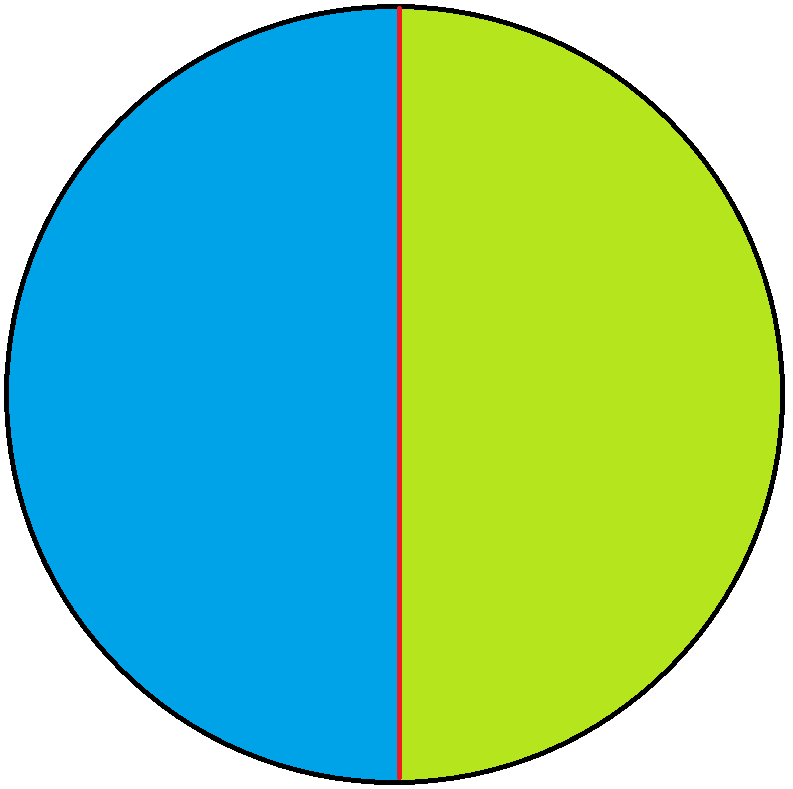
当我们加入第二条边时,当前已有的两个部分再次被一分为二,总共形成4个部分:

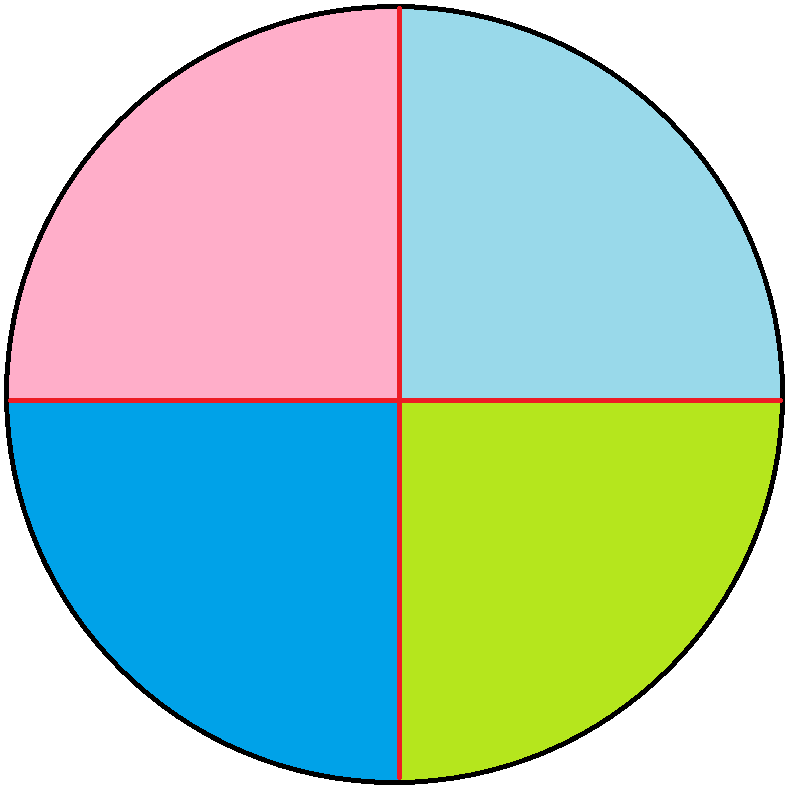
显然,再加入第三条边时,它同样也最多也只能将已有部分中的两个一分为二(你怎么画也不可能经过第三个平面区域),使得总数加2

所以如果有p条相交于同一个点的直线,那么平面最多会被划分为 $ p imes 2$ 个部分.这便是相交于同一点的多条直线的规律.

可以不相交于同一点

如果直线可以不相交于同一点,可以使得最后划分出来的平面数变多嘛?显然是可以的.

可以证明,一定存在一种画法,使得当前这条直线和前面所有的直线相交(此时一定不会过之前已有的任何一个交点),而这时划分出来的平面数时最多的:

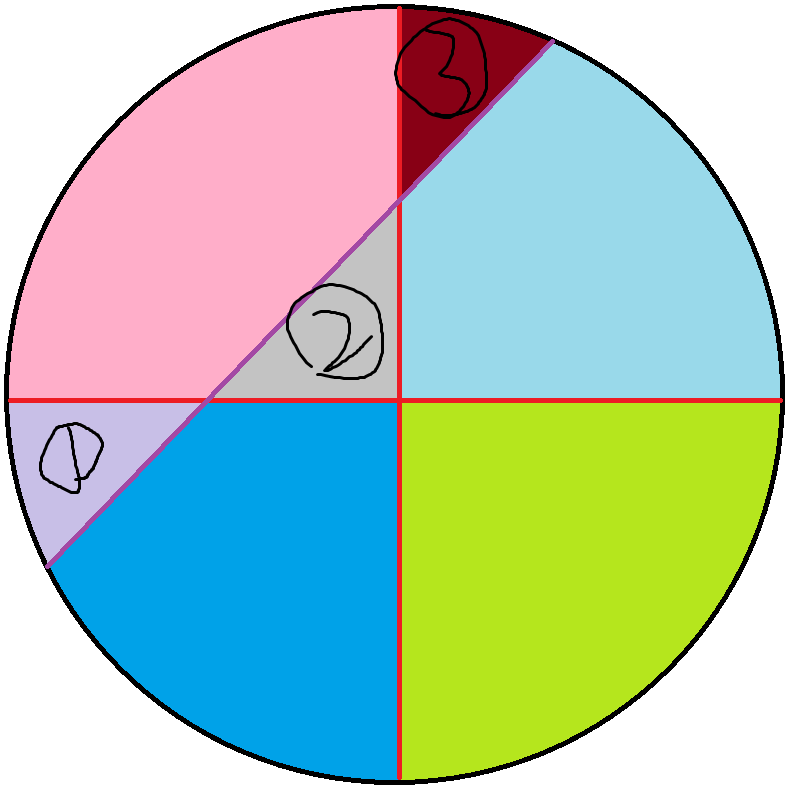
此处这条紫色的直线于原本的两条红色直线相交,可以划分出 $ m + 1 $ (m为原本直线数)个新的部分,也就是 (n) (n为当前总共直线数)个部分.这是因为新的直线和原本每条直线相交时,都可以划分出两个新的部分,但是这两个新的部分中的一个,也可以看成是和下一条直线相交划分出来的,所以除了最后一条直线外(因为他没有下一条直线),每一组都会重复计算一个部分,等效于只能多划分出一个部分,所以总共是多 $ m + 1$ 个部分.

所以初始没有边划分时(即一开始平面区域数量是1),n条可以不相交于同一点的边,可以划分出的平面数量为 $ 1 + 2 + 3 + ... + n = sum_{i = 1}^{n} i = frac{(1 + n) imes n}{2}$ .如果初始时已有p条边进行了划分,那么继续使用n条可以不相交于同一点的边划分可以增加(因为前面p条边的划分方式可以是交于一点的或其他方式,所以我们只能计算增加的)的部分数为: $ (p + 1) + (p + 2) + ... + (p + n) = sum_{i = p + 1}^{p + n} i = frac{(p + 1 + p + n) imes n}{2}$ .这就是可以不相交于同一点的多条直线划分出最大部分数量的规律.

根据上面这两个规律,我们便可以直接通过套用式子,来计算出给定p条相交于同一点的直线和$ n - p $ 条可以相交于同一点的直线时能划分出来的最大平面部分.

参考代码

时间复杂度: (O(1))

空间复杂度: (O(1))

#pragma GCC optimize(1)
#pragma GCC optimize(2)
#pragma GCC optimize(3, "Ofast", "inline")
#include <bits/stdc++.h>

using namespace std;

using i64 = long long;

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);

    int n, p;
    cin >> n >> p;
    n -= p; // 注意n是总直线数,里面同时包含了p,要减掉
    i64 res = (p << 1) + ((p + 1 + p + n) * n >> 1); // 直接利用规律求解即可,<<1等同于除以2,>>1等同于乘2,注意优先级,吃不准还是用除法和乘法好

    cout << res << "
";
    return 0;
}

"正是我们每天反复做的事情，最终造就了我们，优秀不是一种行为，而是一种习惯" ---亚里士多德