[概率论与数理统计]笔记：1.4 条件概率

1.4 条件概率

条件概率

• 样本空间(Omega)
• 事件(A,B)
• (P(B)>0)

在事件(B)已经发生的前提条件下，事件(A)发生的概率称为A对B的条件概率：(P(A|B)).

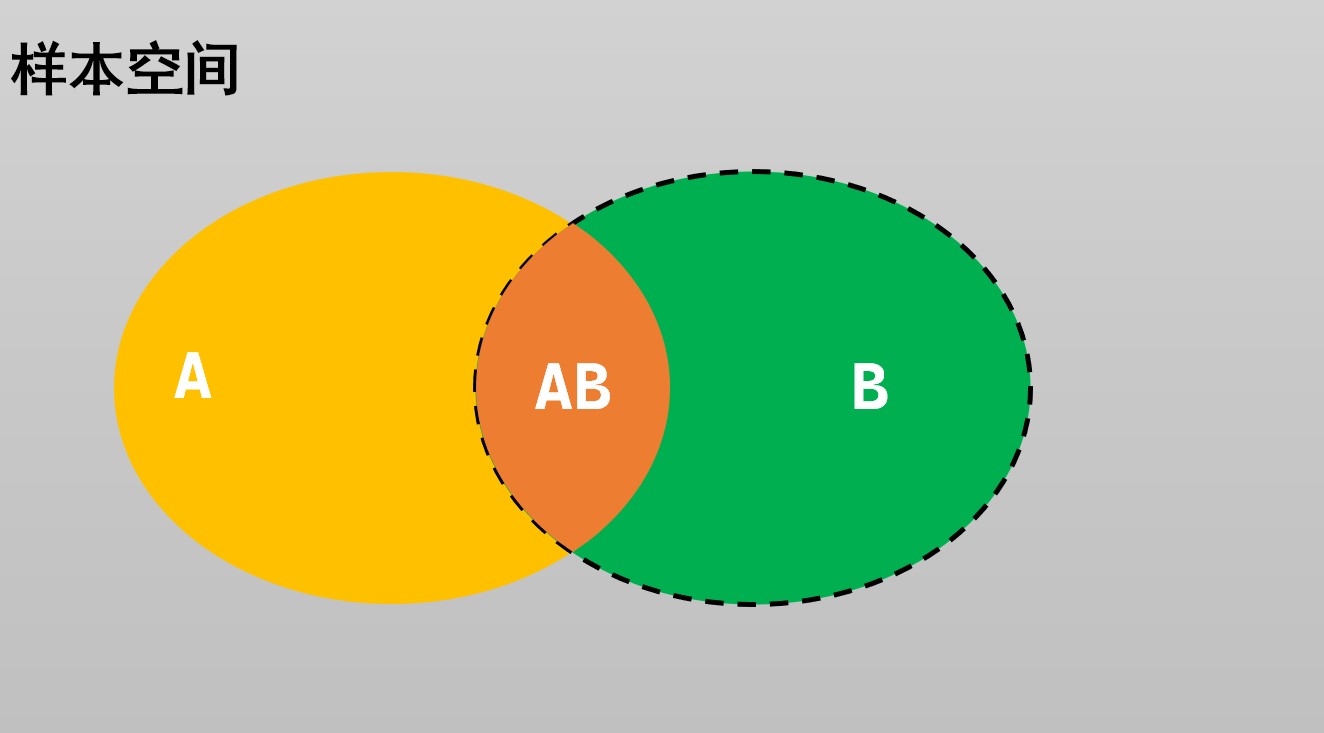
通常，(P(A))为无条件概率，对应的样本空间为(Omega)。

而条件概率(P(A|B))对应的样本空间为(B)，或者记为(Omega_B).

所以：

乘法公式

根据(P(A|B)=frac{P(AB)}{P(B)})可以推导出：

1. (P(AB)=P(A)P(B|A))
2. (P(AB)=P(B)P(A|B))

其中要求(P(A)>0, P(B)>0).

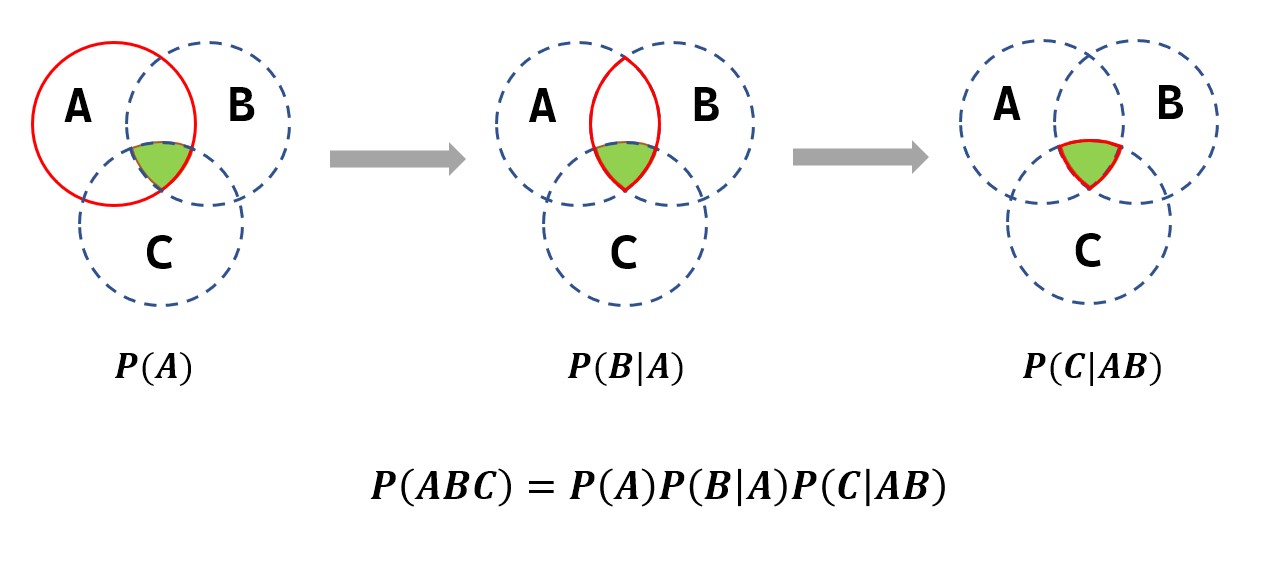
乘法公式可以推广到任意有限个事件：

可以理解为逐步画圈，缩小范围直到精准命中指定交集：（这里用(n=3)为例）

全概率公式

• ({A_i})是(E)的完备事件组。
• (P(A_i)>0)。

则对于任意事件(B)，有：

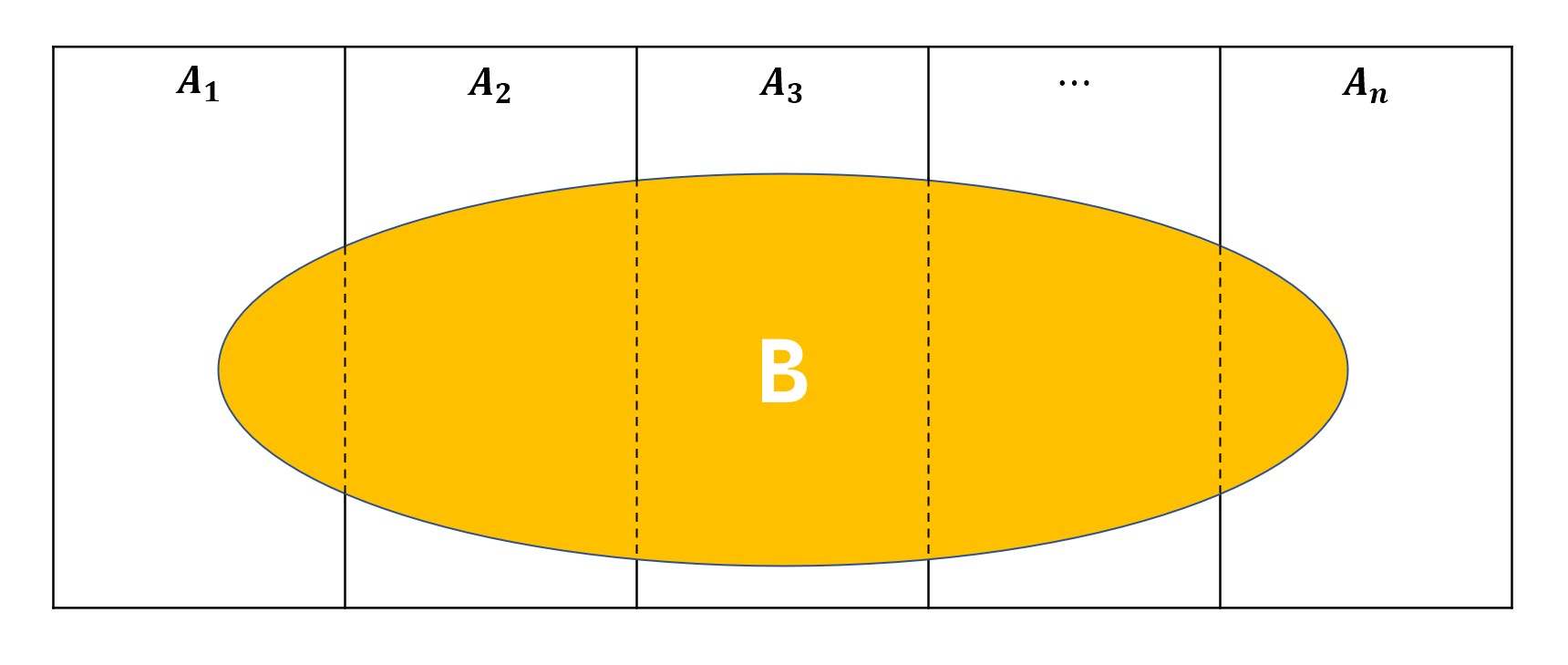
事实上，({A_i})不需要是(E)的完备事件集，只需要满足({A_i})的并集能包住(B)即可。

贝叶斯公式

定义

• ({A_i}) 是完备事件组。
• (P(A_i)>0).

则对于任意事件(B)，(P(B)>0)，有：

• 分子部分：乘法公式
• 分母部分：全概率公式

相关概念

• (P(A_i))称为先验概率（在新信息到来之前）
• (P(A_i|B))称为后验概率（在新信息到来之后）

贝叶斯公式的特点是由果推因，(A_i)是原因，(B)是结果。在已知(B)已经发生的情况下，推测“是(A_i)导致的”的可能性。

举例：

事件(B)是“头疼”，

事件({A_i}=){

​ "劳累过度",

​ "普通感冒",

​ "感染新冠",

​ ......

}

解析：不管事件(B)是否发生，事件(A_i)都有各自发生的可能性，也就是先验概率(P(A_i))。在事件(B)发生之后，后验概率(P(A_i|B))表示“已经头疼了，是由事件(A_i)导致的概率是多少”。

注：在这个例子中：

• (P(A_i|B))表示已经头疼了，是由事件(A_i)导致的可能性是多少。
• (P(B|A_i))表示事件(A_i)已经发生了（比如已经感冒了），那么接下来会“头疼”的可能性是多少。

二者不能搞混。

使用教材：
《概率论与数理统计》第四版 中国人民大学 龙永红 主编 高等教育出版社