[笔记]斜率优化

P0 前言

本来应该早就写了，直到前两天模拟赛又斜率优化的题，才重新学习了斜率优化，故有此文。

P1 斜率优化用来做什么样的题目

适用于把(O(n^2))的线性dp（就是只有一维）优化成(O(n))或者(O(nlog n))。

P2 斜率优化的不等式

不妨先看一道例题。

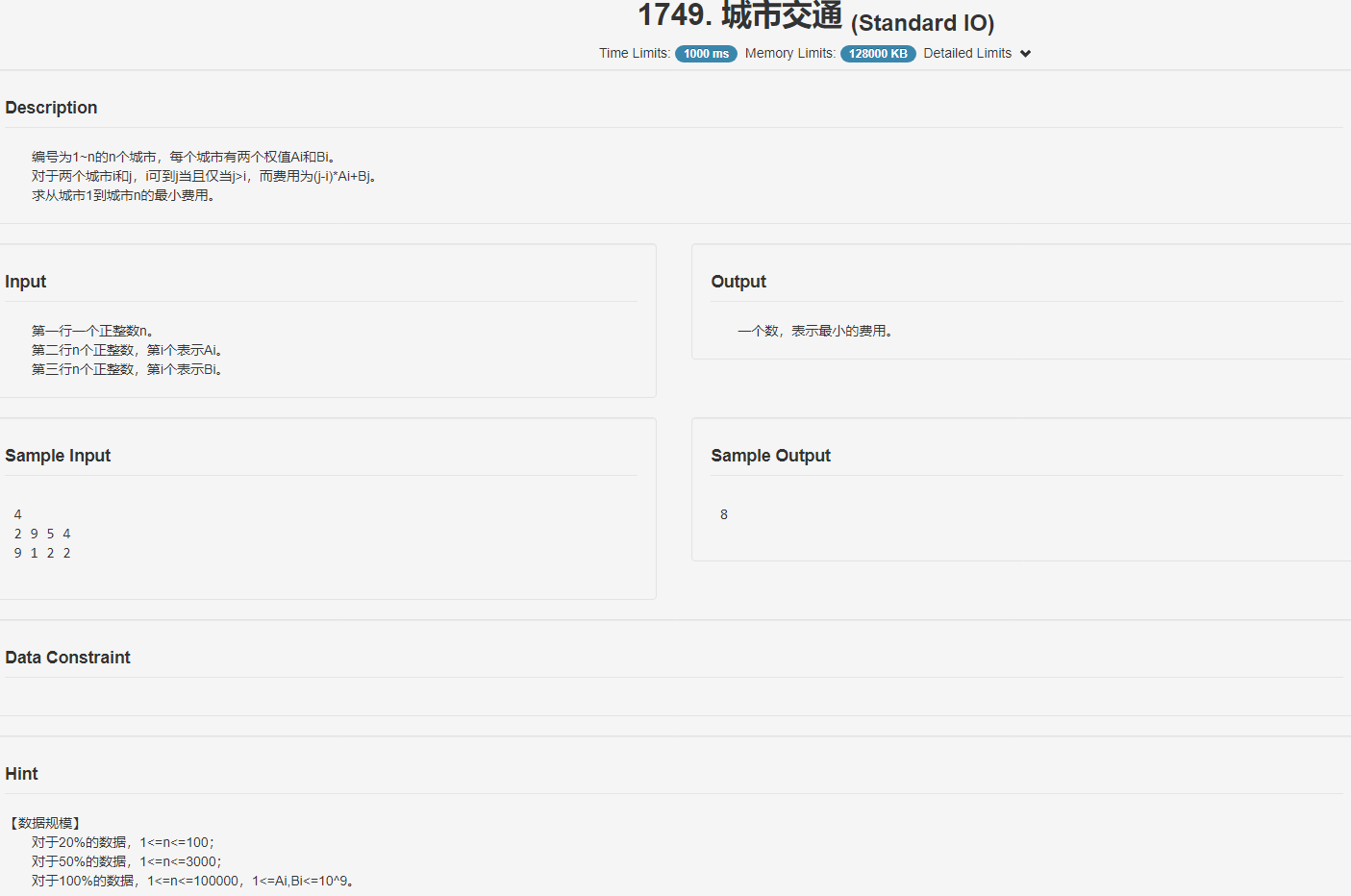
不难设出方程(f[i]=min _{j>i}{f[j]+(j-i)cdot a[i]+b[j]})。这个dp是个倒推，可以理解为反向建边，从n到1.

考虑 (k>j)，并且选择(j)点转移要比选择(k)点转移要优。则有

我们感觉这个式子实在是太复杂了，不妨设(g(j)=f[j]+b[j])，则有

因为(k>j)，所以(k-j>0)，所以再移项时不用变号。

右边可以看做过点((j,g(j)),(k,g(k)))的直线的斜率。令(SL(p_1,p_2))，为过点((p_1,g(p_1)),(p_2,g(p_2)))的直线的斜率。那么上述的不等式可表示为(SL(j,k)>-a[i])。

P2 通过斜率的结论删点加点

从P1可以得到 ( ext{j<k,点j优于点k}Leftrightarrow j<k,SL(j,k)>-a[i])。所以考虑一下下图所示的情况。

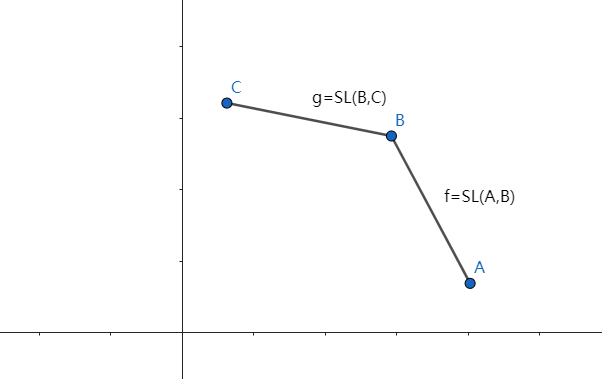
设(g>f,A>B,B>C)，那么考虑B点成为最佳转移点的情况。

1. 对于直线AB而言，f必须满足(f>-a[i])。
2. 对于直线BC而言，g必须满足(g<-a[i])。

根据不等式基本定理，则有(f>-a[i]>gRightarrow f>g)，显然与我们的假设相反。这说明了：在这种情况下，B无论如何都不能成为最佳转移点。此时我们可以把j点删去。

怎么删呢？其实可以用一个单调队列存这些点，队列满足对于队列里任何相邻的三个点(i,j,k,i<j<k,SL(i,j)>SL(j,k))。当然这里可能与下面有出入，但我想表达的意思是对于队列里相邻的三个点，单调队列满足前两个点的斜率大于或小于后两个点的斜率，即斜率是单调地址或者是单调递减的。

那么，我们每算完一个新的点，就可以根据类似于上面的情况，删去那些无论如何都不能成为最佳转移点的转移点。具体来说，就是：

while(SL(x,q[tail])<SL(q[tail],q[tail-1])) tail--;
q[++tail]=x;
\斜率单调递增
while(SL(x,q[tail])>SL(q[tail],q[tail-1])) tail--;
q[++tail]=x;
\斜率单调递减

而这道题要用单调递减的队列，P4会解释为什么。

P3 通过单调性质找点

好的，现在终于可考虑对于点(i)，怎么找最佳转移点(j)了。

就这道题而言，由于它所需的斜率(-a[i])并不是单调的，所以可以通过二分找点。这里有一个小细节，由于我们的dp是倒着推，所以先进队的元素比后进队的要打，具体来说，就是(q[i]>q[i-1])。如果找到一个二分点，满足(SL(q[mid],q[mid-1])>-a[i],SL(q[mid],q[mid+1])le-a[i])，这个就是我们需要的最佳转移点。

解释一下为什么。首先可得(q[mid-1]>q[mid]>q[mid+1])，那第一个不等式就满足了P1推的结论，可得q[mid]要比q[mid-1]优；第二个不等式就不满足，可得q[mid]要比q[mid+1]优。在队列中在(SL(q[mid],q[mid+1]))后面的斜率肯定也要小于(-a[i])，因为它单调递减，所以可得(q[mid]优于q[mid+1]优于q[mid+2]优于...优于q[tail])；在队列中，在(SL(mid-1,mid))之前的斜率肯定也大于-a[i]，因为队列单调递减，所以(q[mid]优于q[mid-1]优于q[mid-2]优于...优于q[1])。通过这些，可以得到，此时(q[mid])就是最佳转移点。

那找点的时间复杂度就是(O(log n))的，对于我们在不等式的所需斜率不是单调的都要(O(log n))的时间来找点，因此此类所需斜率不单调的题目的时间复杂度为(O(n log n))。对于斜率递增的题目，就可以弹队头，知道队头满足不等式的条件，找点的均摊时间复杂度是(O(1))，因此这类问题的时间复杂度是(O(n))。

P4 为什么是单调递减

现在解决P2的问题。假如说，现在我有一个点(w)要加入单调队列，入队时，肯定要把队尾比(SL(w,q[tail]))大的斜率的点删去。可是在P1我们得出了(j<k,SL(j,k)>-a[i])，j才比k优。在后面的dp中，你把那些大斜率都删去了，就剩下一个(SL(w,q[tail]))，而且还不保证(SL(w,q[tail])>-a[i])，就失去了很多大斜率。意思就是我们需要较大的斜率，你现在把较大的删去，剩下些小的，你食不食油饼。与其这样，我们不如把较大的斜率保留，把比现在斜率小的斜率删去，而呈现出来的数据就是单调递减。

那么如何判断是单调递增还是单调递减呢？可以画几幅图，像P2那样的，一幅斜率单调递增，一幅斜率单调递减，像P2那样讨论一下，看一下那一幅是可以删点的。

P5 做斜率优化题的技巧

1. 看看数据，看是不是那种卡(O(n^2))，不卡(O(n)或者O(nlog n))的题。
2. 考虑(j<k)，j比k优或者(k<j)，j比k优的情况，列不等式。
3. 把不等式化简，用一个函数表示仅和j、k有关的式子，另外不管。
4. 一般来说，剩下的项可以合并，注意一下最后不等式要写成斜率的形式，可以乘或除-1。
5. 考虑单调递增还是单调递减，画一下，讨论一下。一般来说，横坐标递增则递增；横坐标递减则递减。
6. 不等式所需斜率没有单调性二分；有的话一般最佳转移点在队头，不过要先出队一些元素。
7. 记得做完一个点要入队。